Study on the Stability of an Artificial Stock Option Market Based on Bidirectional Conduction

Abstract

Although stock option markets have grown dramatically over the past several decades, the relation between an option and its underlying asset, especially bidirectional conduction, is not particularly clear. So far, there have been many debates about this topic. We try to investigate this problem from a novel angle: an artificial stock market including a stock option is constructed in this paper. The model includes two parts, one is a stock trade module based on the Santa Fe Institute Artificial Stock Market (SFI-ASM), and the other is an option trade module. In the latter module, three types of option traders are employed. The results show that the model is effective, and experiments illustrate that option markets have a remarkable effect on stock markets. Furthermore, by appending options, the model replicates some stylized properties, such as volatility clustering and GARCH effect, which can be observed in real financial markets.

1. Introduction

In the past few decades, there has been an explosive growth on derivative securities in financial markets. The impact of this growth on the World economy is immense and can influence the stability of financial markets. It is clear that there has been a massive increase in both the types of financial derivatives available for trade and the size of transactions involving derivatives. Financial innovations have caused more and more concerns, especially after the 2007 subprime crisis. Many people attribute the cause of the financial crisis to financial innovations which were perceived as being out of control. However, others take the opposite view; they think that financial derivatives can stabilize financial markets. This disagreement emanates from the unclear mechanism of action between financial derivatives and their underlying assets. Options are an important component in a wide variety of financial derivatives. Thus, the option will be taken as research subject in this paper. We focus on the information flow in financial markets and handle it as a continuous diffusion process among market participants between stock market and option market, where the information diffusion is modeled by price and volume. Furthermore, the two financial markets can be considered as a simple network with bidirectional information diffusion.

The original Black and Scholes model [1] was proposed to value European options. In 1973, the Chicago Board Options Exchange (CBOE) was founded and standardized call options were introduced. The impact of the option market on the underlying stock market is very complicated and not clearly understood. Some scholars have focused on this issue, but their conclusions were not unanimous. Some researchers found that the introduction of options had a positive effect on the underlying stock markets. For instance, Hakansson [2] and Ross [3] found that the introduction of options could improve financial market completeness because they expanded the range of choices available to investors. Those authors also thought that options trading could reduce the volatility of the underlying stock. John et al. [4] introduced a model where agents were informed agents and found that an incremental public information made the underlying market more efficient. Similarly, Kumar et al. [5] pointed out that the options markets created higher liquidity and greater pricing efficiency for the underlying stocks. Many other researchers held the similar viewpoints [6,7,8].

On the other hand, some researchers thought that options could destabilize the underlying market and tend to increase stock price volatility. Heer et al. [9] showed that after the introduction of options the variance of the stock return increased. Wei et al. [10] showed that options increased the volatility of OTC stocks. Besides these two viewpoints, many other researchers claimed that the introduction of options did not directly and significantly affect the underlying market. For example, Bollen [11] affirmed that the introduction of options did not significantly affect stock return variance. Kabir [12] also studied the impact of option introduction. He pointed out that the introduction of options resulted in a significant decline in stock price, but had no significant effect on volatility.

All results were based on traditional methods. In recent years, a new approach-an agent based model-for studying financial markets has appeared. Agent-based computational economic and financial modelling is completely different from conventional economic modelling. For an agent-based model, the basic premise changes from a classical representative, rational agents to behavioral, boundedly rational and heterogeneous agents who use experience to forecast the economic situation. Currently the Santa Fe Institute Artificial Stock Market and Genoa Artificial Stock Market (GASM) models are two of the most popular agent-based models. Many researchers have used these two models to study many economic and financial issues [13,14,15]. However, there is very little research using these models to examine the effect of option markets on stock markets.

Ecca et al. [16] presented the first study on the effects of an option market related to an underlying stock market, using an artificial financial market based on heterogeneous agents investigated a realistic European option by two market models. Their results showed that the introduction of options, in the proposed models, tended to decrease the volatility of the underlying stock price. Moreover, the traders’ wealth can be strongly affected by using option to hedge risk.

However, the above research still has shortcomings. For example, the stocks used in Ecca et al.’s paper did not pay dividends, unlike many stocks that pay periodic dividends in real stock markets. Besides, the option traders are only allowed to buy options from the market maker who has infinite wealth. In order to overcome the above shortcomings, we will use SFI-ASM to build an option trade market and introduce some trading mechanisms into the model to more closely replicate actual options markets.

This paper focuses on the effect of option markets on stock markets. The rest of the chapters are organized as follows: Section 2 is the introduction of our model and the section is mainly divided into three parts. Section 3 reports the results of our experiments. Finally, our conclusions and recommendations of future works are summarized in Section 4.

2. The Model

In this section we focus on the new model which includes two modules. First, the stock trade module will be introduced and its limitations will be pointed out. Then, the compound Poisson process will be employed to construct a dividend process. Finally, the option trade module will be presented.

2.1. Stock Trade Module and Its Limitations

2.1.1. The Introduction of the Stock Trade Module

This model consists of two parts, the first part is a stock trade module, and the second part is a stock option trade module. The following is the introduction of the stock trade module which is based on SFI-ASM.

In this module there are two assets. One is a stock and the other one is a riskless asset. In every period the riskless asset holders receive an interest payment and interest rate denoted by r_f = 0.1. Similarly, stock holders can receive stock dividend which is generated by a stationary stochastic process and the equation of dividend process is denoted as Equation (1):

$$d_t=\rho d_{t-1}+(1-\rho )\overline{d}+{\epsilon }_t$$

(1)

where ${\epsilon }_t~N(0,{\sigma }_e^2)$, the expected value of dividend, $E(d_t)=\overline{d}$ (10.0), the variance of dividend, $D(d_t)={\sigma }_e^2/(1-{\rho }^2)$(0.074), the correlation coefficient of dividend, ${\rho }_{d_t{d}_{t-1}}=\rho$(0.95).

The agent utility function is constant absolute risk aversion (CARA) $U(W_{t+1})=-e^{-\gamma W_{t+1}}$ (γ is risk aversion parameter and equals to 0.5), the agent will maximize the expected utility function in the next period:

$$\max E_t[U(W_{t+1})]$$

(2)

Subject to (there are only one stock and one riskless asset):

$$W_{t+1}=x_{1,t}(p_{1,t+1}+d_{1,t+1})+(1+r_f)(W_t-x_{1,t}{p}_{1,t})$$

(3)

Solving Equation (2), we can get the demand of stock of each agent in the current time period:

$$x_{1,t}=\frac{[E_t(p_{1,t+1}+d_{1,t+1})-(1+r_f)p_{1,t}]}{\gamma Va{r}_t(p_{1,t+1}+d_{1,t+1})}$$

(4)

where:

$$E_t(p_{1,t+1}+d_{1,t+1})=a(p_t+d_t)+b$$

(5)

In the module every agent has 100 forecast rules with different $a$ and $b$ values, so they can forecast the expected value of $(p_{t+1}+d_{t+1})$ by Equation (5). When agents make predictions about the future price and dividend, they choose the proper forecast rule from the rule set according to previous stock information which includes the time series of stock price and stock dividends. In the forecast rule set for the agent, rules with bad prediction will be replaced by new forecast rules which are generated by a Genetic Algorithm (GA) at regular time intervals [17,18]. This time interval represents the learning speed and the reaction speed of agents to market changes. In our model the time interval equals 250, because the major purpose of this paper is to study the effect of option markets on stock markets, so the learning speeds of all the agents are same. $Va{r}_t(p_{1,t+1}+d_{1,t+1})$ is the conditional variance of the agent’s forecast, in the module, it is updated at the end of each loop:

$$Va{r}_t(p_{1,t+1}+d_{1,t+1})=bvVa{r}_{t-1}(p_{1,t}+d_{1,t})+av{(p_{1,t+1}+d_{1,t+1}-E_t(p_{1,t+1}+d_{1,t+1}))}^2$$

(6)

Where av and bv are weight coefficients.

The stock price is given by a market maker who gathers supply and demand information of all the agents and constantly adjusts the demand and supply to achieve equilibrium. The $d_t$ has been determined before the $p_t$ is given, from the Equations (4) and (5) the change of $p_t$ can causes the $x_{1,t}$ to change.

In the module it is important that if agents are identical with parameters, a homogeneous linear rational expectation equilibrium (REE) exits, at the moment the stock price is a linear function of dividend:

$$p_t=f{d}_t+e$$

(7)

where:

$$f=\rho /(1+r_f-\rho )$$

(8)

$$e=\frac{\overline{d}(1+f)(1-\rho )-\gamma {\sigma }_{p+d}^2}{r_f}$$

(9)

$${\sigma }_{p+d}^2={(1+f)}^{2}D(d_t)$$

(10)

For the REE, a and b of Equation (5) can be denoted as follows:

$$a=\rho$$

(11)

$$b=(1-\rho )(1+f)\overline{d}+e$$

(12)

2.1.2. The Limitations of the Stock Trade Module and the Countermeasure

This paper mainly researches the interaction between an options market and its underlying asset market. In the model the mechanism through which the stock market impacts the option market is obvious because the stock price directly influences the options pricing. However the way in which the option market impacts the stock market is not clear. During the construction of model and through many experiments we find the limitations of the stock trade module.

Equation (4) shows that the only variable which determines the stock demand is $p_t$. So we presume that stock demand is unrelated to agent wealth $W_{t-1}$ and the stock holding $x_{t-1}$ in the previous period. Then, we will verify the assumption by the experiments. There are two groups of experiments. First, the influence of the agent’s wealth will be tested by the change of the initial cash of agent which is the same to all the agents when the experiment begins. Second, the influence of the agent’s stock holding will be tested through the stock random swap among the agents. Results of our experiments are given in Table 1.

Table 1. The statistics of stock price under different initial cash scenarios.

Initial cash	20	200	2,000	20,000
Average	98.47	98.41	98.27	98.27
Variance	3.34	3.48	3.45	3.45

Table 1. The statistics of stock price under different initial cash scenarios.

Initial cash	20	200	2,000	20,000
Average	98.47	98.41	98.27	98.27
Variance	3.34	3.48	3.45	3.45

In this paper the interaction effects between the stock market and the option market are mainly researched through the changes in the time series of the stock price. The length of data used in Table 1 is 50,000 periods and the data is adopted after the model starts to stabilize. Table 1 shows that the change of initial cash does not obviously cause a change in stock price.

Next, we performed the second experiment for the stock holdings of agents redistributed randomly at regular intervals. Our purpose is to observe the changes of stock price. In the experiment, the time interval equals 100 periods. The time of model running is more than 200,000 period and experiment takes the 100,000th period as a transition point; before 100,000th period the stock holdings are not artificially redistributed, and after 100,000th period the redistribution is carried out. The results of experiments are given in Figure 1 and Table 2.

Figure 1. The price time series of stock (1,000th is transition point).

Figure 1. The price time series of stock (1,000th is transition point).

Table 2. The statistics of stock price before and after the stock holdings are redistributed.

	Before	After
Average	98.27	98.42
Variance	3.45	3.54

Table 2. The statistics of stock price before and after the stock holdings are redistributed.

	Before	After
Average	98.27	98.42
Variance	3.45	3.54

Figure 1 shows that whether an agent stock holding is redistributed or not, the basic state of the REE does not change. Table 2 confirms this result and shows that the statistics of stock price change are very little. Therefore, we conclude that the redistribution of stock holdings will not change stock price. The above results confirmed our hypothesis that stock price is unrelated to initial cash and distribution of stock holdings. Therefore, we can make the two variables constants in later experiments.

The proposed model in this paper includes two parts, a stock trade module and an option trade module. They are not synchronized and the stock is traded before the stock option is traded in every period. When options are exercised, this results in the redistribution of wealth and stock holdings among all agents, but according to the above analysis the two variables cannot influence the stock pricing in the next period. The effect of the option market on the stock market is a very small unidirectional transmission, so we need to construct their double-way relationship from another perspective. We will research this problem from an information angle because the information plays a significant role for asset pricing. This idea can be supported by some empirical results [19,20,21]. As mentioned above, during the decision-making process agents use information including both stock price and stock dividend. The price and volume information of option market will be used to influence the agent’s decision-making and construct the effect of option market on the stock market. This is accomplished by the addition of option information into Equation (5):

$$E_t(p_{1,t+1}+d_{1,t+1})=(a+{\delta }_{t-1})(p_t+d_t)+b$$

(13)

where ${\delta }_{t-1}$ synthesizes the information of the option market, which includes option prices and option trade volumes in multi-periods. In the option trade module two options are introduced, call options and put options for the same underlying asset:

$${\delta }_{t-1}=\gamma ({\kappa }_1{\phi }_{t-1}+{\kappa }_2{\phi }_{t-2}+\mathrm{...}+{\kappa }_s{\phi }_{t-s})$$

(14)

where $\gamma$ is a weight coefficient and greater than zero, which represents the stock market impact of option market, the bigger the value of $\gamma$, the bigger the effect is. ${\kappa }_1,{\kappa }_2,\mathrm{...},{\kappa }_s$ are also weight coefficients of information in different periods and ${\kappa }_1+{\kappa }_2+\mathrm{...}+{\kappa }_s=1$, the subscript $S$ is the length of information used in the model:

$${\phi }_{t-1}=0.25{\psi }_{\text{t-1,}1}+0.25{\psi }_{t-1,2}-0.25{\psi }_{t-1,3}-0.25{\psi }_{t-1,4}$$

(15)

where ${\psi }_{\text{t-1,}1}$ and ${\psi }_{\text{t-1,2}}$ denote the price information and the volume information of call options, ${\psi }_{\text{t-1,3}}$ and ${\psi }_{\text{t-1,4}}$ denote the price information and the volume information of put options, respectively:

$${\psi }_{\text{t-1,i}}=\{\begin{array}{l}1x_{t-1,i}>x_{t-2,i}and{x}_{t-2,i}>x_{t-3,i}\\ -1x_{t-1,i}<x_{t-2,i}and{x}_{t-2,i}<x_{t-3,i}\\ 0others\end{array}i=1,2,3,4$$

(16)

where $x_{t-1,i}(i=1,2,3,4)$ denotes call option price, call option volume, put option price and put option volume, respectively.

The important role of the option market is price discovery. The above definition implies that if call option price or volume has a sequential two-period increase, it will create a positive expectation for the stock market, which can herald an increase of stock price and vice versa. The put option market is similar to it, but the effect is the opposite. That is to say, Equations (13)–(16) describe an information diffusion process from an option to its underlying asset.

2.2. The Compound Poisson Process

In the real stock market, stock prices will rapidly fluctuate due to a variety of factors. The jumped process is introduced in the dividend process of stock to make it closer to real financial markets. According to the Equation (7), the change of dividend will inevitably be reflected in the stock price after the arrival of the REE.

On the basis of Equation (1), the new dividend process is generated by a compound Poisson process. If the jump range equals to 1, a Poisson process occurs, it is denoted as $N(t)$, and its strength equals to $\lambda =0.01$. So the compound Poisson process can be constructed as $Q(t)={\displaystyle \sum _{i=1}^{N(t)}{Y}_i}$, $t\ge 0$, where $N(t)$ is the Poisson process and its strength equals to $\lambda$, $Y_1,Y_2,Y_3\mathrm{......}$ are i.i.d. normal random variables. In this paper their expected values equal to 10 and variances equal to 0.7225.

The experimental results show that the model could reach a steady state REE. The data in Table 3 and Figure 2 is run from 20,000 periods after the system starts to stabilize. From the above data we can find that the change of average price is small, but variances of the dividend and stock price vary widely, and the change of stock price is bigger than the dividend process. The experiments address that after the compound Poisson process is introduced, mutagenicity of stock price appears. Moreover, the corresponding parameters also need to be recomputed in the stock trade module because the variance of dividend has changed. In our model, the stock trade module also adds the compound Poisson process.

Table 3. The statistics of dividend and stock price.

	Old dividend process	New dividend process	Old stock price	New stock price
Average	10.0	10.0	97.85	96.59
Variance	0.074	0.1463	5.05	15.23

Table 3. The statistics of dividend and stock price.

	Old dividend process	New dividend process	Old stock price	New stock price
Average	10.0	10.0	97.85	96.59
Variance	0.074	0.1463	5.05	15.23

Figure 2. The time series of stock dividend (left: old stock price, right: new stock price).

Figure 2. The time series of stock dividend (left: old stock price, right: new stock price).

2.3. The Option Trade Module

In order to research the effect of stock options on the stock price, we will append stock options into the model, and then it will be introduced in detail from several aspects.

2.3.1. The Setting of Option

In the paper the European option is used, and according to the actual situation, the option’s lifetime equals three months, because every month has in practice about twenty days in which stocks can be traded. Therefore, the horizons equals to 60 days and the option will be exercised after 60 days. Here one day is defined as the time length in which model runs once. In our model the put options and call options are allowed to trade among the agents.

The option premium is computed by B-S Equation with stock dividend. Volatility of the stock price is computed through the historical stock price series, the length of data used equals to lifetime of option, and volatility will be recomputed as the model moves forward. The strike price of the option is fixed at the beginning of the option issue. It equals to the stock price added or subtracted to a value which is decided by the stock price. During the lifetime of the option the strike price will not be changed. The strike price is set by $X\in \{p_t-\alpha ,p_t+\alpha \}$.For a call option $X=p_t+\alpha$ and for a put option $X=p_t-\alpha$. The value of $\alpha$ depends on the current price $p_t$ and $\alpha$ equals to 1.5 in the paper.

2.3.2. The Types of Option Traders

The option trade agents are divided into three types in the model. They are random option trader, speculation option trader and hedge option trader, respectively.

Random option trader represents the noise trader existing in the real market. A noise trader makes irrational and erratic decisions to buy, sell, or hold options. The presence of noise traders in financial markets can cause prices and risk levels to diverge from expected levels even if all other traders are rational [22]. In our model, random option traders decide randomly to buy or sell options and the types of options and the size of option contract are also decided randomly.

Hedge option traders are agents who want to cover stock options through holding option contracts. In the model they can buy put options or sell call options to lock market risks. The hedge option trade continually adjusts their holding options to make their stock position equal to the sum of all option contracts unless the agents do not have sufficient cash to pay the option premium and option margins, so the stock risk can be covered. But there is an implicit assumption which is that stock price remains invariant during the time the option is held. The following Equation determines the option demand for the hedge option trader at the current time:

$$d_t=s_t-{\displaystyle \sum x_{i,t-1}}$$

(17)

where d_t denotes the current option demand, s_t denotes the current stock position, x_i,t-1 is the quantity of different types option in the previous time (t−1) and if call option was bought or put option was sold by agent the item is negative, if call option was sold or put option was bought the item is positive, all items are summed to obtain the option demand in the current time.

Speculation option traders are entirely the opposite of hedge option trader. These agents will hold option contracts the same with the holding stock position, so they will earn additional profit; nevertheless, they will also face more serious risk when the stock price fluctuates. The following Equation is the option demands:

$$d_t=s_t+{\displaystyle \sum x_{i,t-1}}$$

(18)

The variables represent the same values as Equation (17).

2.3.3. The Option Market Maker

When the option market maker is introduced to the model, it collects the option demands of all agents and accomplishes the option trade. It also executes mark to market at option validity period, and exercises options at the expiring day. In our model the maker does not buy and sell options to participate the option trade, instead it only acts as a medium.

(1) Option trade mechanism

The call option and put option are simultaneously traded in the market. Before the options are traded, every type of agents first decided the trade demands of option; then they set the price they were willing to pay for the trade. As we know, the option price can be computed by B-S Equation in which the only uncertain variable is volatility. Therefore, agents forecast stock volatility to get the option price. The following equation shows how each type of option traders forecast volatility.

$${\sigma }_t=\{\begin{array}{l}{\sigma }_{h,t-1}+\alpha {\epsilon }_t^1\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}speculation option trader}\\ {\sigma }_{c,t-1}+\beta {\epsilon }_t^2\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}hedge option trader}\\ \frac{1}{2}({\sigma }_{c,t-1}+{\sigma }_{h,t-1})+\gamma {\epsilon }_t^3\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}random option trader}\end{array}$$

(19)

where ${\sigma }_t$ is the stock volatility used to compute the option price at the current time, ${\sigma }_{c,t-1}$ is the volatility which is computed through past stock price series and ${\sigma }_{h,t-1}$ is the implied volatility which is computed by the last option price. ${\epsilon }_t^i~N(0,1)$. So as to embody the characteristics of different kind of option traders, $\alpha >\gamma >\beta$ is set. Equation (19) reveals that during the volatility forecast the speculation option traders’ focus on long-term considerations and the hedge option traders are more concerned with the short-term changes of option price, which is analogous to traders in real financial markets.

After every option trader gets the demand or supply and price of the option, the marker counts up the demand and supply of every option respectively, to get the supply and demand curve of each option. The option price and volume are decided by intersection of two curves. This can be called Multi-Agent matchmaking mechanism. Figure 3 is the schematic of supply and demand curve.

Figure 3 shows that the trade volume of option is about 1.5 and the option price is about 3.

(2) Mark to market

In accordance with the real option market, a daily mark to market system is incorporated into the model. Before the options start to trade, mark to market is executed. When agents sell an option they will deposit margins in their margin account which is in the marker. If agents buy the option the margin is not necessary, they only pay the option premium. Here naked options are used.

Figure 3. The supply and demand curve of call option.

Figure 3. The supply and demand curve of call option.

If the cash in the agent’s margin account is less than the required current margin, the agent will be forced to deposit money in their margin account. If agent does not have enough cash, its option contract will be executed in advance. If the cash of an agent margin account is more than the required current margin, the agent is allowed to withdraw extra money from agent margin account.

The ratio coefficient—leverage ratio used in margin computation is defined as a variable, so we can adjust the variable to study its effects on the option market.

(3) Exercise option

Market makers exercise options that are in-the-money at expiration. Unlike real option markets, in our model the underlying share of option is not exchanged upon expiration. Instead, the option is exercised through an exchange of cash. After the options are exercised, some agents get a profit and some agents get a loss. The cash transfer will lead to the redistribution of wealth among agents. Thus, the next period stock trade will be affected and a change in features of stock market will also occur. Similarly, the stock trade also affects the option trade through changes in the wealth and position of agents. There is a close two-way relationship between stock market and option market. Next it will be tested by experiments. Figure 4 is the time line of a market day.

In Section 2, we have constructed a simple social network which includes two subnetworks. One is stock market which has agents with different wealth. Another one is option market which has three different kinds of investors, speculation option trade, hedge option trade and random option trade. In the former subnetwork, an agent can be considered as a node of social network, and the market maker is a special node in the network which guarantees other nodes can receive and send information (price and volume of stock). Similarly, in the latter subnetwork, option information is transmitted between the different types of traders by the marker maker. Furthermore, option and stock information can be transmitted between the two subnetworks.

3. Experiments

In this section we focus on the new model which includes two modules. First, the stock trade module will be introduced and its limitations will be pointed out. Second, the compound Poisson process will be employed to describe the dividend process. Finally, the option trade module will be presented.

Figure 4. The time line of a market day (the X-axis represents time).

Figure 4. The time line of a market day (the X-axis represents time).

3.1. Experimental Parameters

This section mainly introduces the various parameters used in the experiments. 200 agents were used in the model. In the stock trade module, the size of agent’s forecast rules set is 100. Other detailed main parameter values are in Table 4.

Table 4. Parameter values of stock trade module.

Parameter	Parameter value	Parameter	Parameter value
$\overline{d}$	10.0	$a$	0.95
$\rho$	0.95	$b$	4.5053
$D(d_t)$	0.1463	$a$ range	0.7–1.2
$f$	6.3333	$b$ range	−10.2945–19.7053
$e$	16.7732

Table 4. Parameter values of stock trade module.

Parameter	Parameter value	Parameter	Parameter value
$\overline{d}$	10.0	$a$	0.95
$\rho$	0.95	$b$	4.5053
$D(d_t)$	0.1463	$a$ range	0.7–1.2
$f$	6.3333	$b$ range	−10.2945–19.7053
$e$	16.7732

The main parameters used in the option trade module are set out in Table 5. In addition to the parameters mentioned above, other parameters will be briefly introduced. “Option start time” is moment at which option trading begins; the purpose of this parameter is to start to run the option module after the stock price has become stable. Because when the model starts to run, the price of stock fluctuates wildly. “Stocks per contract” is the number of stock contained in per option contract.

Table 5. Parameter values of option trade module.

Parameter	Parameter value	Parameter	Parameter value
lifetime	60	Leverage Ratio	0.2
Option start time	10000	$\lambda$	0.01
Stocks per contract	1.0

Table 5. Parameter values of option trade module.

Parameter	Parameter value	Parameter	Parameter value
lifetime	60	Leverage Ratio	0.2
Option start time	10000	$\lambda$	0.01
Stocks per contract	1.0

3.2. The Stability of the Model

Before comparing in detail the differences between the stock market and the option market, we first analyze the stability of model with options. In the experiment after the running period of the stock trade module equals 5,000 the option trade module starts to run. The model is executed more than 200,000 periods without any interruption.

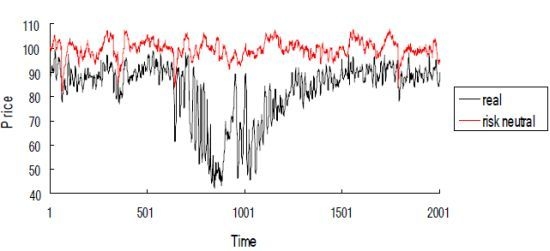
Figure 5 is price time series of stock from the 0th period to the 20,000th period. In Figure 5 “real” price represents the price obtained through stock trade, “risk neutral” price represents the price obtained by equation ($p_t^r=d_t/r_f$). Figure 6 is the forecast error time series of stock price of the first agent from the 0th to the 20,000th period, the forecast errors of stock price of the other agents have the same change tendency.

Figure 5. The price time series of stock.

Figure 5. The price time series of stock.

Figure 6. The forecast error time series of stock price of the first agent.

Figure 6. The forecast error time series of stock price of the first agent.

From Figure 5 and Figure 6 we can see that the system remains stable from the 5,000th period. When the stock option starts to trade at the 10,000th one, the time series has not obviously changed and the system continues to remain stable. The forecast error becomes very small as the stock price tends to stabilize and after 50,000th period the forecast error of every agent is less than 2.0.

3.3. The Effect of Option Market on Stock Price and Volume

Next we will analyze the effect of the option market on the stock market. So as to compare directly, the 100,000th period is taken as a transition point. Before the 100,000th period, the option trade is not included and after 100,000th period the option trade starts to run.

Figure 7 illustrates the stock price time series which are chosen from a long stable price sequence. From Figure 7, we can find the obvious difference between the two cases. After the option is introduced, the price volatility becomes higher and the spread of the real price and the risk neutral price becomes larger. The result implicates that option information (price and volume) impacts on the real price of stock. That is to say, the option market affects the stock market by information diffusion through the network.

Figure 7. The price time series of stock. (left: before the option is introduced; right: after the option is introduced).

Figure 7. The price time series of stock. (left: before the option is introduced; right: after the option is introduced).

From the statistical data of Table 6, we can find the obvious difference between the two states, especially in variances. From the stock price, we can find that the average of stock price decreases after the stock option starts to trade. However, variance decreases more, which fits the fact that the higher the income, the greater the risk. A stock’s yield is the dividend per share divided by its current price per share. Before the option is introduced in the model, the stock average yield equals the average dividend divided by stock price. The value equals to 11.13% (10.0/89.81). After the option is introduced, the stock average yield is 12.48% (10.0/80.12).

Table 6. The statistics of dividend and stock price.

	Stock price without option	Stock price with option	Trade volume without option	Trade volume with option
Average	89.81	80.12	14.81	11.96
Variance	10.40	20.31	230.12	115.98

Table 6. The statistics of dividend and stock price.

	Stock price without option	Stock price with option	Trade volume without option	Trade volume with option
Average	89.81	80.12	14.81	11.96
Variance	10.40	20.31	230.12	115.98

When average trading volume decreases, the variance also decreases, unlike the change in price. The increase of risk in owning the stock and the relatively unstable stock price causes the agents to tend to hold cash. This decreases both the variance of the trade volume and the average of trade volume.

The preceding analysis illustrates that the introduction of stock options cannot stabilize market price, so the variance of price increases. Therefore, the risk in owning stock becomes large, which leads to a decrease in the price of the stock. However, it should be pointed out that our conclusion is drawn based only on our model. Before the option is introduced, the stock trade module has reached the REE, though the compound Poisson process is introduced.

3.4. The Effect of Option Market on Stock Return and Volatility

This section mainly studies the changes of the features of stock return series market when the option market is introduced. The features of stock return include volatility persistence and fat tails or excess kurtosis.

At frequencies of less than one month, the unconditional returns of financial series are not normally distributed in the real market. They usually display a distribution with too few in the mid-range, too many observations near the mean, and again, too many in the extreme left and right tails. This feature discovered by Mandelbrot [23] has puzzled financial economists. Recently, return distribution has obtained more attention in risk management because the computation of value at risk of stock needs relative correct return distributions.

Stock returns are normally calculated by the following expression, $r_t=\ln (p_t/p_{t-1})$, $p_t$ is the current stock price. But in our model the computation of stock return needs to be adjusted because a dividend is paid each period, which is not common in the real stock market. The stock dividend is also paid, but time intervals are far longer. In our model we use $r_t=\ln ((p_t+d_t)/p_{t-1})$ to calculate the stock returns; d_t denotes the current stock dividend. Figure 8 is stock price return time series which are chosen in a long stable price sequence. The sample size in Table 7 is 50,000.

Figure 8. The time series of stock logarithmic returns. (left: before the option is introduced; right: after the option is introduced).

Figure 8. The time series of stock logarithmic returns. (left: before the option is introduced; right: after the option is introduced).

Table 7. The statistics of dividend and stock logarithmic return.

	Stock return without option	Stock return with option
Average	0.105579	0.120366
Variance	0.000346	0.000937
Kurtosis	22.1443	14.49292

Table 7. The statistics of dividend and stock logarithmic return.

	Stock return without option	Stock return with option
Average	0.105579	0.120366
Variance	0.000346	0.000937
Kurtosis	22.1443	14.49292

From Figure 8 and Table 7 we can find that the difference between the two stock returns obviously. Before the option is introduced, the stock returns change gently as a whole, because of the introduction of the compound Poisson process. There are some sudden changes in the stock return, which makes the kurtosis become very large. After the option is introduced, the average stock return and volatility increase, but the kurtosis also decreases. The shape of stock return is closer to the real stock return. Stock return distributions show obvious fat tails or excess kurtosis (kurtosis > 3) whether or not the stock option is introduced. The results show that the excess kurtosis and fat tail has nothing to do with the introduction of options. In addition, option trading really has an impact on the return of stock. Conversely, the fluctuation of stock price can continually affect the option market.

Next we will analyze the volatility of the stock which is an important parameter in the stock market. Volatility cannot be observed directly, but it has some important features such as the persistence of volatility that lacks a widely accepted explanation. In order to analyze the volatility, we use the conditional volatility models which seem to be appropriate.

The GARCH model was proposed initially by Bollerslev [24]. The GARCH model largely consists of two parts, the mean equation and conditional variance covariance equations. The mean equation used in the paper is ARMA model. The conditional variance covariance equations used is the GARCH(1,1) model which has been proven to be an adequate representation for most financial time series by Lamoreux and Lastrpes [25]:

$$ARMA(p,q)\mathrm{model}:\hspace{0.17em}{r}_t={\gamma }_1{r}_{t-1}+\mathrm{...}+{\gamma }_p{r}_{t-p}+a_t+{\theta }_1{a}_{t-1}+\mathrm{...}+{\theta }_q{a}_{t-q}$$

(20)

$$GARCH(1,1)\mathrm{model}:\hspace{0.17em}{a}_t={\sigma }_t{\epsilon }_t,{\sigma }_t^2=c+{\alpha }_1{a}_{t-1}^2+{\beta }_1{\sigma }_{t-1}^2$$

(21)

where ${\epsilon }_t$ follows $N(0,1)$, $a_t$ follows $N(0,{\sigma }_t^2)$, $c\ge 0,{\beta }_1\le 1,{\alpha }_1+{\beta }_1<1$.

We firstly build the ARMA model by using EVIEWS software measurement model parameter estimation and testing. The parameters of the ARMA model are as shown in Table 8 and Table 9.

Table 8. The parameters of ARMA model before option is introduced.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.105579	5.28E−05	2000.599	0.0000
AR(1)	−0.138857	0.012371	−11.22476	0.0000
MA(1)	−0.232591	0.012149	−19.14488	0.0000

Table 8. The parameters of ARMA model before option is introduced.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.105579	5.28E−05	2000.599	0.0000
AR(1)	−0.138857	0.012371	−11.22476	0.0000
MA(1)	−0.232591	0.012149	−19.14488	0.0000

Table 9. The parameters of ARMA model after option is introduced.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.119826	0.000857	139.7441	0.0000
AR(1)	1.718534	0.011286	152.2778	0.0000
AR(2)	−0.51085	0.023445	−21.7891	0.0000
AR(3)	−0.61926	0.01682	−36.8165	0.0000
AR(4)	0.409515	0.004987	82.11901	0.0000
MA(1)	−1.53815	0.012256	−125.502	0.0000
MA(2)	0.392182	0.023032	17.0278	0.0000
MA(3)	0.16174	0.011836	13.66452	0.0000

Table 9. The parameters of ARMA model after option is introduced.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.119826	0.000857	139.7441	0.0000
AR(1)	1.718534	0.011286	152.2778	0.0000
AR(2)	−0.51085	0.023445	−21.7891	0.0000
AR(3)	−0.61926	0.01682	−36.8165	0.0000
AR(4)	0.409515	0.004987	82.11901	0.0000
MA(1)	−1.53815	0.012256	−125.502	0.0000
MA(2)	0.392182	0.023032	17.0278	0.0000
MA(3)	0.16174	0.011836	13.66452	0.0000

In Figure 9 and Figure 10, the stock return residual refers to the residual after the ARMA is built. From Figure 9 we can see that the Serial correlation of the residual doesn’t exist after the ARMA is built. Conversely, in Figure 10 the Serial correlation of residual squares does exist, which shows that the ARCH effect exits in the stock return series. To analyze this observation objectively, we carry out the statistical test of the ARCH effect. Like the results displayed in Figure 9 and Figure 10, the statistical test results show that there is an ARCH effect in the logarithmic return series and the results passed the significance test at the 1% level.

Figure 9. The autocorrelation of the stock return residual series. (left: before the option is introduced; right: after the option is introduced).

Figure 9. The autocorrelation of the stock return residual series. (left: before the option is introduced; right: after the option is introduced).

Figure 10. The autocorrelation of the stock return residual squared series. (left: before the option is introduced; right: after the option is introduced).

Figure 10. The autocorrelation of the stock return residual squared series. (left: before the option is introduced; right: after the option is introduced).

The specific parameters of the model are in Table 10 and all parameters pass the 1% significance level test.

Table 10. The parameters of GARCH (1,1) model.

Parameters	$c$	${\alpha }_1$	${\beta }_1$
Before	0.000168	0.429756	−0.00509
After	1.62E−05	0.058384	0.914057

Table 10. The parameters of GARCH (1,1) model.

Parameters	$c$	${\alpha }_1$	${\beta }_1$
Before	0.000168	0.429756	−0.00509
After	1.62E−05	0.058384	0.914057

From Table 10, we can see that the stock’s volatility persistence is clearly demonstrated through the ARMA-GARCH(1,1) model, whether the option is introduced or not. Yet the results also show that after the stock option is introduced, the parameters of ARMA-GARCH(1,1) model have changed. Because the purpose of the introduction of GARCH model is to analyze return volatility, we mainly focus on conditional variance covariance equation. The sizes of the α₁ and β₁ coefficients represent the strength of volatility persistence. After the option is introduced the α₁ value decreases, but the β₁ increases more, so in general, return volatility persistence becomes more obvious following the introduction of the option. Furthermore, more information has been transmitted from option market to stock market which is the reason of increases of volatility in stock market.

3.5. The Effect of Various Information Length

From Equation (14) we can see that the length of previous option market information is a variable. In this section we will change this variable to study its effect on the stock market. We carried out a series of six experiments and the detailed parameters used in the experiments are as shown in Table 11. In the parameter setting for the latest information (t-1) of the option market the greater weighing coefficient was given and the other times the weighing coefficients are equal. The coefficient of the latest information continues to decrease with information accumulation.

Table 11. The weighing coefficients of information at different times in the model.

Weighing coefficients	t-1	t-2	t-3	t-4	t-5	t-6
1	1.0	/	/	/	/	/
2	0.6	0.4	/	/	/	/
3	0.5	0.25	0.25	/	/	/
4	0.4	0.2	0.2	0.2	/	/
5	0.3	0.175	0.175	0.175	0.175	/
6	0.2	0.16	0.16	0.16	0.16	0.16

Table 11. The weighing coefficients of information at different times in the model.

Weighing coefficients	t-1	t-2	t-3	t-4	t-5	t-6
1	1.0	/	/	/	/	/
2	0.6	0.4	/	/	/	/
3	0.5	0.25	0.25	/	/	/
4	0.4	0.2	0.2	0.2	/	/
5	0.3	0.175	0.175	0.175	0.175	/
6	0.2	0.16	0.16	0.16	0.16	0.16

In Equation (14) γ is also a parameter which represents the extent of the stock market’s impact on the option market. The larger the value of γ, the bigger the effect, but the model can become more volatile. If the value of γ is small, the effect is not obvious; so the selection of appropriate value is very important. The parameter will be determined through a series of experiments whose results are contained in Table 12. Table 12 shows that when the information of the option market is introduced, the stock price varies widely with γ increase. When γ equals to 0.03 the average decreases sharply and the variance increases dramatically, the model becomes unstable. Thus, the value of γ should be less than 0.03. If γ equals 0 the option market information is not introduced. Considering these two conditions, the value of γ equals to 0.02 in the model. Therefore, at this point, the model is stable and the effect of option market on stock market is appropriate.

Table 12. The statistics of stock price under different γ.

γ	0.0	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
Average	89.59	89.23	89.11	65.55	56.28	45.67	37.17	30.34	23.89	21.23
Variance	9.979	11.89	12.05	54.85	64.93	87.67	98.07	92.57	109.09	97.02

Table 12. The statistics of stock price under different γ.

γ	0.0	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
Average	89.59	89.23	89.11	65.55	56.28	45.67	37.17	30.34	23.89	21.23
Variance	9.979	11.89	12.05	54.85	64.93	87.67	98.07	92.57	109.09	97.02

After γ is determined we will study the effect of various information lengths on the stock market. Table 13 is the statistics of stock price under different information length scenarios. We can see that the average price increases along with an increase of information, but the variance is decreasing. This shows that the information of the option market is a key factor in the model. The increase of information for traders can decrease fluctuations of the stock price. For example, when information length increases from 1 to 2, the mean of stock price increases 16.28% and the variance decreases 24.80%; when information length increases from 5 to 6, the mean of stock price increases 1.36% and the variance decreases 21.44%. After comparing the mean and variance of price, we found that if the variance of stock is high, the stock price is low, and the effect of information diffusion is degressive, which corresponds to the real stock market.

Table 13. The statistics of stock price under different information lengths.

Information length	1	2	3	4	5	6
Average	62.48	72.65	79.15	84.32	87.46	88.65
Variance	30.81	23.17	24.78	24.92	21.22	16.67

Table 13. The statistics of stock price under different information lengths.

Information length	1	2	3	4	5	6
Average	62.48	72.65	79.15	84.32	87.46	88.65
Variance	30.81	23.17	24.78	24.92	21.22	16.67

Moreover, in the experiments we also find that when the information about the stock option market is introduced and after running a longer period of time, the model stabilizes. There are still big fluctuations in price in some situations. Figure 11 is the price time series of stock whose running time is more than 150,000. From Figure 11 we can find that there is a downward change in the stock price. At this moment the stock dividend has not changed much. This phenomenon tells us that even though the introduction of the option market can stabilize the stock markets, there is still much information and complexity that can lead to dramatic changes in the stock market.

Figure 11. The trade volume time series of stock.

Figure 11. The trade volume time series of stock.

3.6. The Effect of Various Proportions of Option Traders

In this subsection we focus on the effect of the proportions of option traders. Parameter γ equals 0.02, the length of information is 6 and the agent number is 200. The other parameters are the same as those in Table 4.

In real financial markets there are different kinds of option traders whose purposes are different and whose strategies are relative complicated. So as to more closely represent a real market, there are three types of option trader in this model. Their option trade strategies are different and relatively simplified.

In Table 14 the expression “0.15-0.15-0.35-0.35” represents the proportion of four types of option traders which are non-option traders, random option traders, hedge option traders and speculate option traders, respectively. In Table 14 the other expressions have similar meanings. In the experimental design, we pay much more attention to the speculative option trader and the hedge option trader than to the non-option trader and the random option trader, so many experiments will be done about the proportion changes of two types of agents changes. The sample size is 50,000.

Table 14. The statistics of stock price under different proportion of option traders.

Proportion	Average	Variance	Proportion	Average	Variance
0.25-0.25-0.25-0.25	87.197	63.410	0-0-0.6-0.4	91.510	13.661
0.15-0.15-0.35-0.35	88.038	48.726	0-0-0.5-0.5	89.389	16.170
0.05-0.05-0.45-0.45	89.737	16.555	0-0-0.4-0.6	89.394	14.506
0-0-0.9-0.1	98.431	12.975	0-0-0.3-0.7	89.125	14.016
0-0-0.8-0.2	97.487	12.718	0-0-0.2-0.8	89.371	14.180
0-0-0.7-0.3	96.462	13.062	0-0-0.1-0.9	89.359	16.088

Table 14. The statistics of stock price under different proportion of option traders.

Proportion	Average	Variance	Proportion	Average	Variance
0.25-0.25-0.25-0.25	87.197	63.410	0-0-0.6-0.4	91.510	13.661
0.15-0.15-0.35-0.35	88.038	48.726	0-0-0.5-0.5	89.389	16.170
0.05-0.05-0.45-0.45	89.737	16.555	0-0-0.4-0.6	89.394	14.506
0-0-0.9-0.1	98.431	12.975	0-0-0.3-0.7	89.125	14.016
0-0-0.8-0.2	97.487	12.718	0-0-0.2-0.8	89.371	14.180
0-0-0.7-0.3	96.462	13.062	0-0-0.1-0.9	89.359	16.088

Table 14 shows that the changing proportion of traders does influence the stock market. Decreasing the non-option traders and random option traders can stabilize the stock market. The system becomes stable when the non-option and random option traders are less than 5%, respectively. Under these conditions, the variance rapidly decreases and the average price increases. This shows that as more people participate in stock option trading, with the exception of random traders, the stock market becomes more stable. The random option trader is a negative factor to stabilization of the stock market. Increasing proportions of this type of trader can make stock market more volatile. We can draw a conclusion that random option trader is a significant factor of the system stable because it transmit noise between option market and stock market. The noise not only is diffused among agents in the option market, but also transmitted in the stock market.

From the proportion of the hedge and speculate option traders the result shows that the increase of hedge option traders can stabilize the stock market. Conversely, the increase of speculate option traders can make the stock market more volatile, which fits the fact existing in the real financial market, so the correctness of the constructed models is proved.

4. Conclusions and Future Work

In order to study the effect of option markets on stock markets, we presented a model of a European option market in this paper. This new model overcomes some shortcomings and better replicates some features of real option markets. To construct a two-sided impact mechanism, we introduced the option market information into the stock market. Here, the two markets form a simple network with information diffusion which is a key factor in the process of price and volume in both markets. Most importantly, the compound Poisson process is introduced to the dividend process which is similar to the real dividend process. Moreover, the results show that mutagenicity of stock price appears which can also be observed in real financial markets.

In this model, three types of option traders were proposed. In the pricing mechanism, the Multi-Agent matchmaking tradeoff model is firstly introduced to more closely mimic to the real option market. The experiments show that the simulation system is reliable after operating for longer time periods.

The experiments show that the introduction of options could make the average of stock price decreases and stock price variance increases. For stock returns, we found that both the average and the variance increase despite a decrease in kurtosis. Stock return distributions show obvious fat tails or excess kurtosis. Through the estimation of GARCH after the option is introduced, the persistence of volatility becomes obvious. We also find that the average price is increasing with an increase of information, but the variance is decreasing. This proved the importance of information provided by the option market in the model. The increase in information for traders can decrease fluctuations of the stock price. However, other information and the complexity of market can still lead to dramatic changes in the market.

Using different proportions of hedge and speculate option traders, the result shows that the increase of hedge option traders can stabilize the stock market. On the other hand, an increase in the proportion of speculative option traders can make the stock market more volatile which is consistent with results from real financial markets, so the correctness of constructed models is proved.

It should be pointed out that our conclusion is based on our model. Before the options are introduced, the stock trade module has reached REE, though the compound Poisson process is introduced. The next stage of the research is to employ heterogeneous agents to capture some other stylized facts.