Signal Processing for the Measurement of the Deuterium/Hydrogen Ratio in the Local Interstellar Medium
Abstract
: We report on a comprehensive signal processing procedure for very low signal levels for the measurement of neutral deuterium in the local interstellar medium from a spacecraft in Earth orbit. The deuterium measurements were performed with the IBEX-Lo camera on NASA’s Interstellar Boundary Explorer (IBEX) satellite. Our analysis technique for these data consists of creating a mass relation in three-dimensional time of flight space to accurately determine the position of the predicted D events, to precisely model the tail of the H events in the region where the H tail events are near the expected D events, and then to separate the H tail from the observations to extract the very faint D signal. This interstellar D signal, which is expected to be a few counts per year, is extracted from a strong terrestrial background signal, consisting of sputter products from the sensor’s conversion surface. As reference we accurately measure the terrestrial D/H ratio in these sputtered products and then discriminate this terrestrial background source. During the three years of the mission time when the deuterium signal was visible to IBEX, the observation geometry and orbit allowed for a total observation time of 115.3 days. Because of the spinning of the spacecraft and the stepping through eight energy channels the actual observing time of the interstellar wind was only 1.44 days. With the optimised data analysis we found three counts that could be attributed to interstellar deuterium. These results update our earlier work.1. Introduction
Measurements of the interstellar wind by the Interstellar Boundary Explorer (IBEX) satellite [1] in Earth orbit provide a supplementary means to observe the D/H ratio in the local interstellar medium for telescopic observations. According to the standard cosmological model, deuterium was produced in significant amounts only during primordial nucleosynthesis within the first 100–1,000 s of the universe. It is destroyed in the interiors of stars much faster than it is produced by the other natural processes that produce insignificant amounts. Over time, baryonic matter is processed in stars where deuterium is destroyed by nuclear reactions (astration). Deuterium-poor and metal-rich material is returned to the interstellar medium in supernova explosions and stellar winds. Nearly all deuterium found in nature is believed to have been produced in the Big Bang. Within our galaxy, deuterium is removed from interstellar gas through astration and possibly through the depletion of deuterium onto dust grains, and replenished by the accretion of pristine material onto the galaxy [2–5]. As a result, measurements of the D abundance in different locations of the galaxy provide important tests for models of primordial nucleosynthesis and for the chemical evolution of the galaxy and intergalactic medium.
The mean deuterium abundance in the low density Local Bubble within 100 pc is D/H = 15.6 ± 4 ppm [6]. However, Linsky et al. [6] have found that deuterium abundances in the global interstellar medium vary within a factor four, with a complex dependence on hydrogen column densities. Before IBEX, the deuterium abundance in the Local Interstellar Cloud (LIC) could only be investigated using spectroscopic measurements of the heavily blended deuterium and hydrogen Lyman alpha lines towards nearby stars. The closest star representing the LIC is Sirius, where the D/H ratio of 16 ± 4 ppm is typical of the Local Bubble interior [7]. In our initial analysis, the D/H measurements by direct sampling on IBEX were found to be consistent with the Sirius measurements [8]. Here we present the details of the analytical technique and an updated D/H value for the Local Interstellar Medium (LISM).
1.1. Interstellar Wind at 1 AU
The LISM consists of warm, relatively dilute, partially ionised interstellar gas surrounding the Sun [9–11]. The Sun moves through the low density, warm, partially ionised LIC, where fluxes of far ultraviolet radiation are high, the fractional abundance of deuterium in molecular form is expected to be insignificant.
The Sun continuously ejects coronal plasma as a solar wind (mostly protons and electrons together with frozen-in solar magnetic field that inflates a plasma bubble in the interstellar medium known as the heliosphere. The heliosphere effectively excludes the LISM plasma from the nearest 100 AU around the Sun. The interaction between the solar wind and LIC determines the shape and structure of the heliosphere (e.g., [12,13]); exploring this interaction is one of the major scientific objectives of IBEX [1].
Neutral interstellar atoms of the interstellar wind have different fates as they interact with the Sun and the solar wind plasma, which affects the transport and survival of the atoms from the LISM to 1 AU. While approaching the inner heliosphere, the interstellar wind is depleted of many neutral species by ionisation processes, and also affected by the Sun’s gravitational field (modified by radiation pressure for H and D). The characteristic flow pattern and density structure that is formed has a cavity close to the Sun, and particles experience gravitational focusing on the downwind side for all species except H [14,15]. Ionisation processes that affect the interstellar neutrals are: ultraviolet (UV) photoionisation, charge exchange (CEX) with solar wind ions, and electron impact ionisation [16–19]. However, with respect to the energy dependent charge exchange cross section we note that the speeds of the cold H and D atoms are nearly stationary compared to heliospheric ions (protons and alpha particles) that could CEX with them. Thus, the physical parameters of interstellar neutrals can be directly measured and provide the best paradigm for modelling and understanding the interplanetary environments of astrospheres [14].
In the case of helium, the dominant ionisation process is UV ionisation outside of 1 AU, and within ∼1 AU there is a steep radial dependence of electron impact ionisation that produces large ionisation rates [20]. He flows through the heliospheric boundary mostly unimpeded because it has a high ionisation potential and low cross section for CEX with solar wind alpha particles and protons.
In contrast, for hydrogen, a substantial fraction interacts with the plasma in the heliosheath via charge exchange: in the outer heliosheath with the interstellar proton population, which is compressed against, the heliopause and in the inner heliosheath with the solar wind protons. CEX losses are much larger than losses by UV ionisation [16], with both processes having a solar cycle dependence. In addition to being a loss process for neutral H and D in the heliosphere, CEX also results in the creation of the secondary population of neutral H and D, which are neutralised protons and deuterons from the outer heliosheath [12]. Both the primary and secondary populations enter the heliosphere, where they are subject to strong CEX and photoionisation losses. As a result, most of the neutral hydrogen becomes ionised and does not reach 1 AU where IBEX is located. At 1 AU, the residual interstellar wind is composed mostly of helium [21], with a small fraction of hydrogen and others constituents, whose abundances relative to helium decrease with increasing solar activity because of filtration.
The cross sections for photoionisation, CEX, and electron impact ionisation of D are practically identical to that for H, thus leading to identical H and D ionisation rates [22]. However, the dynamics do differ [22,23]: (1) the thermal speed of D vTh,D in the LIC is smaller, vTh,D = vTh,H/ [23], thus the reaction rates are slightly different [23]; and (2) the radiation pressure does not counterbalance gravitational effects as it does approximately for H. In addition radiation pressure is a strong function of radial velocities of individual D atoms relative to the Sun because of the Doppler effect and the non-flat profile of the solar Lyman-α emission line that supplies the Lyman-α flux in the heliosphere. By contrast, owing to its larger atomic mass and much weaker flux in the resonant solar 58.4 nm line, He is not affected by radiation pressure. Effectively, the radiation pressure for D is expected to be in between the pressure for H and the (zero) pressure for He. Thus, during the IBEX observations along Earth orbit, the peak of the D signal is expected after the peaks of He and O, and before the maximum of H [23].
1.2. Overview of the IBEX Mission
NASA’s IBEX mission was designed to investigate the interaction of the heliosphere with the surrounding interstellar medium via the observation of Energetic Neutral Atoms (ENAs) from a near Earth vantage point [1,24]. The IBEX spacecraft was launched on 19 October 2008 into a highly elliptical, near-equatorial Earth orbit of ∼3 × 50 RE (with RE the Earth radius), to avoid the interference from ENA emission from the Earth’s magnetosphere as much as possible. IBEX is a Sun-pointing, spinning satellite, whose spin axis is re-oriented toward the Sun after completion of each 7–8 day orbit so that complete full-sky ENA maps are obtained over a period of 6 months. IBEX recorded the first all-sky maps of ENAs produced by the interaction of the heliosphere with the local interstellar medium at heliocentric distances of about 100 AU [25–28].
IBEX samples the interstellar wind distributions at 1 AU in a plane that is approximately perpendicular to the Earth-Sun line, which is equivalent to observing ENAs that arrive from the heliospheric boundary or beyond at the perihelia of their trajectories, independent of its flow direction at infinity.
The IBEX payload consists of two single-pixel ENA cameras with large geometric factors, IBEX-Lo [29] and IBEX-Hi [30], whose Fields-of-View (FoV) lie perpendicular to the Sun-pointed spin axis. Their combined energy range is [10, 6000 eV] with overlap between 300 and 2000 eV. A single Combined Electronics Unit (CEU) controls these sensors, stores data, and is the payload interface to the spacecraft bus [1,24].
1.3. Expected Fluxes of Interstellar Deuterium at Earth Orbit
Models of the dynamics of D inside of the heliosphere show that fluxes of D will be entirely in the energy range of IBEX-Lo with deuterium fluxes expected to be quite low, of the order of 0.015 cm−2 s−1 [22]. The resulting D signal is at the level of single counts per year [22,23]. However, Kubiak et al. [23], predict that IBEX-Lo would be able to detect interstellar neutral deuterium for selected times of the year at specific energies. Clearly, it is very challenging to identify these few deuterium atoms, even with the advanced background suppression techniques used in IBEX-Lo [31]. The elemental ratio for interstellar deuterium to hydrogen is expected to be in the range from 10−5 and 10−2 at Earth orbit [22].
1.4. IBEX-Lo Sensor
The IBEX-Lo sensor is a camera for energetic neutral atoms [29,32]. It maximises collection of the relatively weak heliospheric neutral atom signal while effectively suppressing background sources of local ions, electrons, and UV [31]. It detects neutral atoms in the energy range 0.01 to 2 keV in 8 logarithmic steps with wide energy bands. ENAs from the interstellar wind are the brightest ENA signal in the sky, apart from the magnetosphere of the Earth. The backgrounds present in the IBEX-Lo measurements from various sources are well below the signal of the main interstellar neutrals [31].
The sensor entrance subsystem is based on a cylindrical architecture with an annular collimator, which repels electrons and ions, and allows only neutral atoms to enter (Figure 1). Unfortunately, the high voltage for ion suppression failed in flight, thus associated background sources are higher than originally anticipated. The collimater defines a field of view of 7° × 7° in three 90° angular sectors (called the low resolution sectors) and 3.5° × 3.5° in the fourth angular sector (the high angular resolution sector).
A fraction of the interstellar and heliospheric neutrals that pass through the collimator are converted to negative ions in the ENA-to-ion conversion subsystem. The neutrals are converted on a high yield, chemically inert, diamond-like carbon conversion surface [26,33]. The negative ions leaving the conversion surface are accelerated into an electrostatic analyser (ESA), which sets the energy passband for the sensor. The ESA has been designed to accept a large angular range of backscattered and sputtered products from the conversion surface [32]. In normal sensor operations, the eight energy steps are sampled on a 2-spin per energy step cadence so that the full energy range is covered in 16 spacecraft spins.
Finally, negative ions exiting the ESA are further accelerated to 16 keV, and then are mass-analysed in a time-of-flight (TOF) mass spectrometer. The entire TOF ion optics section floats at a post-acceleration (PAC) high voltage of 16 kV. This acceleration voltage helps straighten out negative ion trajectories between the ESA exit and TOF entrance. The high ion energy allows a TOF measurement with sufficient mass resolution after energy loss in the entrance foil [33]. The TOF analysis subsystem is a carbon foil-based TOF ion mass spectrometer that uses a triple coincidence detection scheme, shown in Figure 2. For each registered atom three times of flight (TOF0, TOF1, and TOF2) are measured independently from each other and are subsequently compared to efficiently eliminate background, which is very important for the detection of the low fluxes of the LISM D atoms.
When the negative ions enter into the mass spectrometer they release secondary electrons from the first carbon foil. These secondary electrons are focused on the outermost radial anode of the microchannel plate (MCP) detector and constitute the first start pulse (start 1, a in Figure 2). As the negative ions pass through the first C-foil, a fraction of them become neutral again. The ions and neutrals pass a second C-foil and again release secondary electrons. These electrons are focused on the innermost radius of the MCP and constitute the second start pulse (start 2, or c in Figure 2). Finally, after passing through the second C-foil, the ions and neutrals strike the MCP. The signal from these ions and neutrals constitutes a stop pulse (stop, or b0 to b3 in Figure 2).
TOF0 is the time of flight of the ion between the first start and the stop signals (or the time obtained between the C-foil 1 and the MCP). TOF1 is the time between the second ultrathin carbon foil and the MCP detector, where the ion is detected. TOF2 is the time between the first and the second carbon foil. The TOF2 section has a higher mass resolution than TOF1, because only the energy and angular straggling from the C-foil 1 affects the mass resolution. The TOF3 is the delay line signal. TOF3 (anode 3) determines the quadrant where the stop signal is registered. Each TOF is determined separately and encoded to 11 bits (0.16 ns resolution, [29]).
An ion measured in a single TOF section (TOF0, TOF1, or TOF2) is referred to as a double coincidence measurement (one of two possible starts and a stop). An ion that is measured in all three TOF channels satisfies the triple coincidence (requires both the two start and a stop signals). Additionally, valid triple events are required to pass a checksum test, which establishes that the TOF needed to cover the distance from the C-foil 1 to the stop in MCP is about equal to the sum of the TOF required from the first to the second C-foil and the TOF measured between the C-foil 2 and a stop (effectively requiring that TOF0 ≈ TOF2 + TOF1) to assure consistency for a real particle moving properly through the IBEX-Lo TOF unit. This checksum test assures that background from cosmic rays and other penetrating radiation is effectively removed. However, the checksum test leaves a range of possible TOFs for each time of flight channel to account for energy and angular straggling in the carbon foils. Details of this detection technique are given in earlier publications [29,34]. The triple-coincidence detection is designed to effectively reject random background while maintaining high detection efficiency for negative ions. In this analysis we only use valid triple events.
The triple coincidence TOF spectrometer of IBEX-Lo determines the mass of incoming neutral atoms directly for those species that are turned into negative ions at the conversion surface (e.g., H, D, and O). For our purpose it is important to note that noble gases (e.g., He and Ne) do not produce enough negative ions for detection or none at all. However, they are detectable through sputtered negative ions H, C, and O, which are released from the conversion surface [35,36]. Since the IBEX-Lo sensor was also calibrated for its response to He and Ne at a variety of energies [29,35], the observed ratios of H, C, and O can be used to infer the identity (He or Ne) of the incoming neutral atoms [37].
The sputtered H and O atoms occur because the conversion surface of the IBEX-Lo sensor is permanently covered with at least a monolayer of terrestrial water, originating from the outgassing of the sensor. The internal pressure of IBEX-Lo is estimated to be around 10−8 mbar even in space [31]. At this pressure, the water layer would be replenished within ∼103 s, if it were somehow removed (which cannot happen in a sensor always pointed about 90° away from the Sun).
Together with H and O, D is sputtered off the conversion surface according to its abundance in the terrestrial water layer. IBEX-Lo will also detect D− ions with a terrestrial origin that are sputtered primarily by interstellar He atoms, because terrestrial hydrogen is accompanied by 155.76 ± 0.7 ppm of deuterium. Thus, there is a substantial D foreground that competes with purely interstellar D atoms [23]. Therefore, depending on their source, we speak about two types of deuterium collected by IBEX-Lo at 1 AU: a terrestrial component, which is the product of sputtering by interstellar helium, and an interstellar component from the interstellar neutral wind, i.e., external deuterium of interstellar origin. In this analysis we pay careful attention to correctly account for the terrestrial deuterium foreground.
Because the IBEX spacecraft orbits the Earth and its observations are in a plane perpendicular to the Sun-Earth line, there are two opportunities during each year to observe the interstellar wind: first between January and March (Spring season), when the Earth travels into the direction of the gas flow of the interstellar neutral wind, and second between October and December (fall season) when the Earth recedes from the flow direction. In the spring season, the interstellar gas velocity is highest in the IBEX reference frame. This higher velocity compared to the fall season results in higher apparent energy of interstellar atoms, and thus in a higher detection efficiency [29]. In the fall season the relative speed between the interstellar neutral flow and IBEX is low, thus leading to significantly lower efficiency. The optimal time for detection of a faint signal, like D, is thus the spring passage of each year. Tarnopolski and Bzowski [22] predicted a total deuterium flux of 0.015 cm−2 s−1.
2. Data Analysis
2.1. Observation Strategy and Data Selection
To derive the D/H ratio, we used IBEX-Lo data from all the orbits of the spring passage throughout years: 2009, 2010 and 2011. During these years the solar activity increased, appreciably reducing the H signal (and thus also the D signal) in 2011, and producing an even stronger reduction of the H signal in 2012 [38]. The data of the spring 2012 orbits, when IBEX-Lo was operated in a special mode for measuring interstellar O, could not be used for our investigation because of their low H signal.
We use triple coincidence events collected in the four lowest energy channels of IBEX-Lo with central energies E1 = 14.5 eV, E2 = 28.5 eV, E3 = 55.5 eV, and E4= 102 eV, respectively [29]. In energy bins 1 to 3 we find sputtered H and D (i.e., the terrestrial H and D) from interstellar He. Theory predicts that the interstellar deuterium signal is located only in energy bin 3 [22,23] to be observed late during the spring passage. Figure 3 shows two energy H spectra collected with 8 energy bins of IBEX-Lo, with hydrogen raw counts originated from the interstellar He (Orbit 18) and from the interstellar H (Orbit 23). The lowest three energy bins in the H spectrum from He sputtering, show a nearly flat counting trend, which drops steeply in energy bins 4 onwards. Sputtered H signal in energy bin 4 is about a factor 10 lower and correspondingly less D is expected to be collected with this energy step. Thus, energy bin 4 provides an additional test for background where we do not expect to observe any interstellar deuterium signal. This spectrum shows a peak in energy bin 6, which is due to sputtering of interstellar O and Ne [39]. The energy spectrum for interstellar H via direct ionisation on the conversion surface is clearly different from the sputtered H spectrum [21].
2.2. Maxima of Principal Interstellar Wind Components
The origin of the collected deuterium signal varies with ecliptic longitude, since it depends on which is the main component of neutral interstellar wind (helium or hydrogen) during the spring season. The flux maxima for interstellar He, D, and H should be observed by IBEX in temporal sequence along ecliptic longitude. The He and H components show a clear offset in ecliptic longitude of their respective flux maxima, about 35° between the respective peaks [21], which is mainly caused by the differing radiation pressures on He and H [21]. The ratio of radiation pressure to gravitational force progresses from negligible for He, becoming the strongest for H, with D in between [22]. This sequence was validated by observations of the interstellar H and He peaks with the IBEX-Lo data from the first two spring passes in 2009 and 2010 [21], as is shown in the upper part of Figure 4 labelled Measurements. The interstellar neutral D maximum is expected to occur two IBEX orbits after the He signal peak, and approximately one orbit before the H peak [23]. The expected position of the D peak in ecliptic longitude provides a crucial consistency test of our measurement of interstellar neutral deuterium. In the lowest part of Figure 4, labelled Predictions, we show the expected D flux coming from sputtering by interstellar He, which has the similar shape as the signal, scaled by the terrestrial D/H ratio. Also shown is the expected interstellar D signal, which is offset from the interstellar H signal to shorter longitudes and scaled by a D/H ratio predicted by Tarnopolski and Bzowski [22], along with a calculation for the D signal by Kubiak et al. [23].
To summarise, Figure 4 shows the comparison between the existing measurements of the He and H interstellar wind components, and the predicted D signal. The interstellar He peak is stable in longitude, latitude, width, and amplitude from year to year, while the hydrogen peak is observed to vary significantly from year to year [21,38]. The maximum of interstellar He is found in the first and second week of February. Therefore, the maximum of the terrestrial deuterium from the conversion surface must be located also at the same time. The interstellar hydrogen begins to be measured in the last week of February, significantly overlapping with the hydrogen from sputtering by interstellar He. In the first week of March this interference starts to diminish as increasing ecliptic longitude until vanishes. The measurements show that only at the end of the spring passage, when the interstellar wind component is no longer helium (interstellar He is significantly lower), the pure interstellar hydrogen can be measured directly. Then, the deuterium measurement would be almost completely free from additions of helium sputter products, which means that it is unambiguously of interstellar origin.
2.3. Determination of the Deuterium Location in the TOF Spectra—3D-TOF Method
2.3.1. First Approach. Using one TOF Dimension
In the present section, we show the successive development of the analysis method used to obtain the position of a species in the three-dimensional TOF space, and the subsequent counting of the D events at this location [8]. In this description also included are unsuccessful attempts, because they gave us direction how to continue our analysis, so therefore they are an important part of the method as such.
We initially analysed the data collected during individual orbits for the three lowest energy bins of IBEX-Lo, in the three different TOF channels separately. We will be referring to such type of TOF spectra analysis as the one dimensional method. An example for the TOF data and the one dimensional analysis is shown in Figure 5.
The data collected for energy bin 3 of IBEX-Lo during orbit 65 (period of 9–17 February 2010) at the maximum interstellar He flux, are shown as a histogram of spin phase versus day-of-year (DOY) in Figure 6. The spin phase is the heliospheric latitude in spacecraft coordinates with the ecliptic north at a spin phase of 0.5. The signal from the neutral interstellar wind is clearly observed as the horizontal band that crosses from left to right (in DOY) that is centred at spin phase of 0.75 (the ecliptic plane) and spanning in values 0.69 to 0.80. The red rectangle identified shows the selection of data with an optimised range in spin phase for signal-to-noise, which is applied for further analysis. On the right side of Figure 6 we show the histograms of events collected with the lowest four energy bins, against spin phase. The maxima of the interstellar wind signal in energy bin 1 to 3 show clearly a constant value near to 103 events, with an abrupt reduction of counts for energy bin 4 (∼102 events). Such behaviour is expected for the interstellar helium signal and in agreement with calibration [38], see also energy spectrum for interstellar Helium shown in Figure 3. The red dashed lines over the histogram that bracket the rectangle in Figure 6, exclude the base of the signal peak at the level of 1% of the peak value, to optimise the signal/noise ratio.
In Figure 5 we show an example of the TOF spectra for the three TOF channels for energy bin 1 from orbit 65. The asymmetric shapes of the TOF peaks are typical for particles passing through thin carbon foils. When passing thought a carbon foil the ions experience energy loss and angular scattering, where the latter increases the path length of the ion between the carbon foil and the detector, thus the time-of-flight. For energies higher than the mean energy after transmission, the distribution can be described by a Gaussian profile and for energies less than the mean energy the distribution is much broader and features a tail to low energies, i.e., to higher times-of-flight. It can be described, for example by a squared Lorentzian profile [33,40,41].
In all the analyses in one dimension we clearly observe the peaks of the hydrogen, carbon and oxygen in the TOF spectra (Figure 5). The deuterium does not show a visible peak in any case. The deuterium signal is expected to be at the level of counts per year [23], which is significantly below the tail of the hydrogen peak in the TOF histogram for single orbit (see yellow peak in Figure 5). We tried to increase the statistics, i.e., adding data from several orbits and repeat the one dimension analysis with them. For this purpose were used the orbits of the spring passage during years: 2009, 2010 and 2011, which were merged in five groups (i.e., time intervals, given in Table 1), under the following conditions: (1) the first and last orbits of the time intervals covering approximately the same day-of-year and ecliptic longitude in the different years used; (2) the time intervals are sized to maximise statistics yet they provide sufficient resolution in ecliptic longitude; (3) the signal collected during these time intervals is optimised to match the temporal behaviour observed for the H signal from sputtering of interstellar He throughout the spring passage [21], e.g., like-Gaussian curve (minimum in time intervals 1 and 5, and maximum in time interval 3; And finally, (4) the orbits of the end of the spring season, where we expect the signal from the interstellar deuterium, were grouped in the same time interval.
All time intervals are defined as a combination of six successive orbits that share approximately the same observation times in each year, same ecliptic longitude [8]. This combination of six orbits is repeated for the time intervals 1 through 4. Owing to the low expected interstellar deuterium fluxes [22,23], for time interval 5 we combine six orbits in March and April of each of the three years used. In the lower part of Figure 4, we show the different time intervals with their temporal and ecliptic longitude coverage during the spring passage orbits. We applied the one dimensional analysis to this way of data grouping, but the results were similar to those obtained for individual orbits.
Then, we extended the analysis to another orbit grouping, merging the time intervals: in temporal sequence of pairs, those with He as principal component of interstellar wind, and finally created single file with the all the data available, by merging the five time intervals. Unfortunately, the deuterium signal remained below the hydrogen tail despite increasing the statistics. In summary no identifiable deuterium peak was observed with the one-dimensional analysis.
To improve the analysis, we tried a series of indirect methods that should allow extracting the deuterium events from the flank of the hydrogen peak. The first method implemented was to fit a mathematical function to the H peak, subtract the fitted function from the hydrogen signal to isolate the deuterium peak. We fit the hydrogen and other relevant mass peaks, in each of the three TOF spectra for each of the first three energy channels of IBEX-Lo and five orbit grouping intervals to obtain the fit parameters (peak position, area, width, asymmetry, and then FWHM), which were very useful later in the development of the final method. The fit function used was an Exponentially Modified Gaussian (EMG), which correctly describes the observed peak shape in one dimension (Equation (1)). The EMG is a mathematical function resulting from a convolution of a Gaussian with an exponential function:
Although the peak of hydrogen is fairly good natured, a precise fit of this peak with its tail over five decades, was not possible. We spent a lot of time trying to use careful fitting and to do the subtraction, but in the end we had to give up on a D measurement from a single TOF channel. Indeed, the correct isolation of the deuterium events from the H tail has been the biggest challenge faced here in our analysis efforts. In any given single TOF channel, the H peak is wide enough to also have some contribution (though more than three orders of magnitude below the H peak) at the expected D location. After intensely investigating the 1D TOF analysis, we arrived at the conclusions that a direct method of observation of the deuterium signal is not possible, only an indirect method and that comprises the use of the three TOF channels would have any chance of success.
2.3.2. Analysis in Two TOF Dimensions
We created two dimensional TOF histograms that were created from combination of two TOFs, and by collapsing of third TOF dimension. These 2D TOF histograms were also employed for data visualization (see Figure 7, with TOF0 versus TOF2 with TOF1 collapsed), and produced for each energy bin and each time interval. The obvious result of the use of the two TOF dimensions is the significant improvement in the visualisation of the data. When attending to the details, the 2D histogram explains qualitatively why the searching of the deuterium peak with one dimension method did not give a useful result.
The central panel of Figure 7 shows a two dimensional TOF histogram with data that was collected in energy bin 1 during the time interval 3, which is near the maximum interstellar He flux. The centres of the clearly observable peaks (letters designating the species), should be localised on the trend line together with their respective tails. Particles passing through the two C-foils of the mass spectrometer exhibit energy distribution (arising from energy straggling in the C-foil) that tails toward lower energies, i.e., to higher TOFs values [33] and causes two associated TOF tails for each mass peak. In addition to these features we observe secondary tails, and other features that are not observable, and therefore not separable, in one TOF dimension.
A good example how 2D-TOF histogram helps us to analyse the signal structure can be seen in Figure 7 where the horizontal feature, located in the area defined by [40.0, 130.0 ns] in TOF0 and [12.0, 18.0 ns] in TOF2, is a second tail from the H peak. This feature is a background for the D analysis that completely masks the D peak when collapsed to a 1D-TOF0 histogram, as shown in the lower panel of Figure 7. The red lines in this panel show an estimate of the D peak in the D histograms for this measurement. The same situation occurs for the other two TOFs pair combinations (see different panels Figure 8). Thus to minimise the impact of background from these secondary tails on the D signal we rely to a large part on the analysis in three TOF dimensions.
The observed trend line shows that the centres of each species are located on a line in 2D TOF space. We can identify mathematical expressions, i.e., mass equations; that relate the masses of a species with their time-of-flights. These mass equations are derived from their TOF positions, which already were accurately determined by fit in the 1D TOF spectra. The mass equations allow an analytic interpolation to find the TOF position of species not investigated during instrument calibration nor are directly observed in the flight data. The comparison between the locus of deuterium derived by this method and estimates based on instrument simulation [8] were highly favourably.
The mass equations were established as cubic functions that describe the relation between the atomic masses of H, C, and O based on TOF measurements. Initially we used quadratic functions to carry out this task but after completing the entire process, which will be described below, the accuracy of the predicted peak positions for the three clearly observed TOF peaks was insufficient. For that reason we used cubic functions that gave a better approximation. By dropping the linear terms in the cubic functions we achieved the best agreement with the measured peak positions.
The three mathematical expressions that make up the system of equations for TOF0 are listed in Equation (2).We have one set of three equations for each TOF channel (total of nine equations). As independent variables the average of the peak position from the EMG fits of the TOFs of H, C, and O peak were used. It should be noted that the standard deviation of this averages did not exceed 0.4 ns to TOF0, 0.5 ns to TOF2, and 1.5 ns to TOF1, which has the lowest mass resolution.
Since b0, b2, and b3 are unknown coefficients, the system of equations was used to obtain their values, with the atomic masses mH, mC and mO of the three clearly identified species as input. This system of equations was solved using the method of Gauss-Jordan. This procedure was repeated for TOF1 and TOF2. Finally, we define the characteristic TOF mass equations for energy bin 1–4 as follows:
The central panel of Figure 7 shows the centres of the peaks connected by a red line in two-dimensional TOF space (mass relation line), which is determined by the mass equations (Equation (3), by solving for f (TOF0) = f (TOF2)). For this the mass equations were set to zero and their real roots were found in a value range determined by the measured minimum and maximum TOF values [0.0, 300.0 ns]. Then the curve shown depends on the TOF combination that is chosen for the plot (TOFi · TOFj, with i, j = 0, 1, 2; TOF0 and TOF2 in this example). As shown in Figure 7, the model line clearly passes through the centres of the peaks for the identified species. So this line determines a solution that allows us to predict where the centre for a selected mass is located in the absence of a distinct peak.
In an effort to find a compact expression that relates the three TOFs each other, we propose a simplified cubic function (z = a + b · x + c · y + d · x2 + f · y2 + g · x3 + h · y3), to describe the values produced from mass equations for a TOF range between [0.0, 300.0 ns] with steps of 0.01 ns. The result is shown in Equation 4. Unfortunately it has such a high error; its lowest sum of squared absolute is 28.1, so it was not further used.
The 2D-TOF analysis is divided in two parts. Part one deals with the complete review of the signal features, their likely sources, how these features affect the D measurement as background, and how to removing them. To achieve these objectives, we determined the use of total events collected in energy bin 3 in the spring passage during three years (merging data of the time intervals 1 to 5), with which we expect to completely cover the observed signal structures. In part two we analyse the variation of the signal with ecliptic longitude. For this task we selected the data collected in energy bin 3 in two different time intervals to characterise those changes: time interval 3, when the principal component of interstellar neutral wind is He and at its maximum, in comparison with time interval 5 when interstellar neutral wind is basically H.
2.3.2.1. Secondary Tails and Signatures Backgrounds
We can define five structures, which appear in 2D-TOF histogram visualisations that in turn are representations of signal structures in three TOF dimensions:
- (1)
The well-known central feature, i.e., the actual peaks of species, which are directly observed together with their tails, which are close to the mass relation line, the red line in the three panels of Figure 8.
- (2)
The signal arises from particles that knock-off hydrogen atoms from C-foil 2 when passing, which shortens the TOF1 to the hydrogen flight time (best seen in middle lowest panel in left column of Figure 8). The signal is represented by a yellow line in right panels of Figure 8.
- (3)
This signature always appears as a shadow toward the TOF2 axis, especially at carbon and oxygen peaks.
- (4)
The energy loss from charged particles crossing the C-foil 2 produce a second H TOF tail, which is represented bygreen lines in the schematics.
- (5)
The black lines represent the signature of electrons emitted from C-foil 1 by passing particles and these electrons sputtering hydrogen from C-foil 2.
- (6)
The third H TOF tail is created by energy loss in C-foil 1 (represented by blue curves in the schematics). Its path is almost parallel to the mass relation line near the hydrogen peak.
The background features 1 to 4 do not give any contribution to the D measurement in three dimensions, even though in the 1D-TOF representation they completely mask the D signal. The 3D analysis allows separating their apparent contributions from the deuterium signal. The most important background feature in our analysis is the feature 5, which is close to the mass line, thus close to the expected position of D. However, we find that the separation is large enough that the background at the D peak is not detected.
Based on time-of-flight analysis alone, there is in principle, no easy way to distinguish a particle with larger mass going into the mass spectrometer compared to a lighter one that has lost more energy in the C-foil at the TOF entrance. However, the H TOF tail (feature 5 from above list) shows a small angle with the mass relation line, leaving the D signal free of contamination by the H tail. This is easily seen by comparing the left and right panels of Figure 8 for each 2D histogram. Moreover, as will be seen in the next section, the intensity of this tail will be strong reduced at the time interval 5, where is expected to see the signal of interstellar deuterium.
2.3.2.2. Intensity Variations
With the analysis of 2D histograms generated by the data grouped in each time interval of the spring season, it can be concluded that the position of the mass peaks, their associated tails and other features do not change among energy bins and time intervals. However, as it is expected the signal intensity has a substantial variation along ecliptic longitude. This is clearly changing as can be observed when comparing events collected in the same energy bin in two different time intervals. The top panel of Figure 9 shows data from time interval 3 (the maximum interstellar He flux) and in the bottom panel the data of time interval 5 (maximum interstellar H flux), both collected in energy bin 3.
In a qualitative analysis, the H peak and their associated tails are more intense in the time interval 3 than in time interval 5, mostly because of the variation of interstellar He with ecliptic longitude. This variation is remarkable since the H TOF tail contribution from C-foil 1 apparently could partially cover the D measurement, although as was noted above that this tail has an evident separation from the mass relation line. If there is such contribution to D signals at time interval 5, it is strongly reduced due to decrease of signal intensity as can be seen in the bottom panel of Figure 9.
To confirm that the signal only varies in intensity along the elliptic longitude, we take two data samples to calculate the ratio between signal and background at time interval 3 and 5. A first volume was situated at the H peak (Hp) and the other in one of H TOF tail (Ht), we selected the clear signature of energy loss from charged particles crossing the C-foil 2 (feature 3 in above list, shown as a green line in schematics of Figure 8), with a centre approximately situate at 70.0 ns, 55.0 ns, and 15.0 ns for TOF0, TOF1, and TOF2, respectively. The results of the ratio calculation made at time interval 3 is (Hp/Ht)He = 2.05 × 10−2, and at time interval 5 (Hp/Ht)H = 4.13·10−2. These values show that the ratio between signal and background is statistically constant along the ecliptic longitude, despite the strong intensity variation.
2.3.2.3. Alternative Methods
At this point, we have to mention two alternative methods done in 2D-TOF that although they were not successful, gave us a guidance how to continue our analysis. The first method is the subtraction of a fitted H peak from the signal in two dimensions, again with putting particular emphasis on H TOF tail. For this reason, we extend the modelling of the hydrogen peak made with EMG to other asymmetric functions. The tailed functions for which we obtained better results than with the EMG were: Lorentz, Pearson IV, Gauss-Lorentz, and Student T.
The method is schematically is as follows: the H peak is fit in each one dimensional TOF spectra with a tailed function, which produces a group of parameters by each dimension (TOF0, TOF1, and TOF2), later it is selected a TOF combination to analyse (i.e., TOF0–TOF2 collapsing TOF1 in Figure 10), then multiplying the two fit functions with their respective parameters together with the unitary bivariate Gaussian function, giving us a preliminary H peak mask in two dimensions (Equation (5)).
The initial fit function has to be adjusted to the signal before making the subtraction. To accomplish this we selected the same pair combination of TOF flight data and collapse the third TOF. The two dimensional structures of the signal and the initial fit function were overlapping and after several iterations a good fit was accomplished, as indicated by a χ2 minimum, but taking into account the asymmetry parameters, which describes the tail of the peak. Finally, the resulting fit function is subtracted from signal, expecting to set free the D peak in two TOF dimension.
The main problem of matching the H tail is that with a little variation of the asymmetry parameter (i.e., a3 in the EMG function, see Equation (1)) produces a dramatic change in the modelled tail. Contrary to our expectation, the EMG function that worked very well for one dimensional TOF spectra (Figure 6) did not do well in two dimensions (see left and bottom panels in Figure 10). The best modelling was accomplished with Student T function, after several fitting iterations and fixing the position and width parameters of the peak. However, the result proved unsuccessful for a reliable detection of the D signal.
Another approach was to take advance of mass relation line and 3D-TOF space to eliminate the background of secondary tails, leaving only the central volume near mass relation line where the species peaks are observed. The method basically is the selection of events in the vicinity of the mass relation line, and discarding events that are outside of a defined distance to the mass relation line. Thus, we define a range in two TOF dimension selected for analysis (i.e., TOF0–TOF2, shown in Figure 11), based on the mass relation line, from which we calculate two parallels lines (referring to major and minor values respectively in each TOF axis), optimising the distance between them to making sure of take most events from signal are inside and most events from background are discarded. In 3D-TOF analysis, we can imagine two walls running together to mass relation line, which similarly determine two limits for data analysis; the result is a slice which shows the central feature of the signal with the background eliminated. We found that the H tail contribution to the D signal was reduced by three orders of magnitude. Changing the width of this slice, significantly changed the result, which, unfortunately, made this technique too parameter dependent. However, this is still one of the better techniques of examining our three dimensions data.
2.3.3. Collecting the Deuterium Events—3 Dimension TOF
Despite the fact that using just a slice of the data set was not successful to extract the very faint D signal reliably, this technique demonstrates one key element in the data analysis: removal background events of (e.g., the H tail) has to be a crucial element of the analysis. In the next step we try to pick just the deuterium events and avoiding the H tail. This kind of precise cut in 3D-TOF space implies a very small and accurately defined volume for data selection (Figure 12).
To define the size of volume that will be located at the expected location of deuterium in 3D TOF space, we assume that the width of the H and D peak approximately comply with , ≈ , so that we can compute an approximate value of the deuterium peak width with Equation (6). In one dimension the H peak is very clearly identified [8], obtaining its σH values is a straightforward task from the fit parameters, then the range for counting events of deuterium is determined from the sigma σH taking the hydrogen peak as a Gaussian distribution near its top. From the analysis of each TOF channel we obtain σH = 0.6609 ns, 1.2969 ns, and 1.155 ns, for TOF0, TOF1, and TOF2, respectively.
This gives us σD = 0.9347 ns, 1.8341 ns, and 1.6335 ns for the three TOF channels. For two dimensions (whichever possible linear combination between two TOFs), the counting range becomes an ellipse, since the widths of the TOF peaks are different in each TOF channel. Both areas are determined by hydrogen and deuterium sigma, respectively, as was described above. In others words, we are working at the plus-minus one sigma level when collecting events. In three dimensions, we have to simultaneously analyse all three TOFs, the volume allowing us to count the events is an ellipsoid described by Equation (7):
For the ellipsoid centre of deuterium, Ci, we have to make a comprehensive search of the most likely position of deuterium events for the three times-of-flight dimensions, which is based on the mass equations and TOF simulations. These positions can be represented as a small cloud of points in the 3D-TOF space. We also included other possible values we did not take into account before, and we created a grid in 3D-TOF space with a grid spacing of 0.05 ns. The created search cube is defined in nanoseconds as follows: TOF0 = [40.0, 45.0 ns], TOF1= [18.0, 23.0 ns] and, TOF2 = [19.0, 24.0 ns]. Notice as the range of times is very wide, with 5 ns in each TOF dimension. Then, the number of possible deuterium ellipsoid centres for analyses is 106, however, this big number will be strongly reduced by other restrictions.
We analysed the data collected in energy bins 1, 2, 3, and 4 of IBEX-Lo in each time interval of the spring season. Counting at each time interval and their respective energy bins, the H and D events and then calculate the D/H ratio. For this purpose, we create two volumes for counting events, one for the H peak with position and widths completely defined and constants for the whole search procedure, and one for the D peak with widths defined by Equation 7, and with its centre location variable.
The initial stage to find the most likely location ellipsoid centre of deuterium volume was to define some constraints for the D counting results: (1) the number of D events collected at the time interval 5 to energy bins 1 and 2, must be equal or less than one (no signal expected); (2) In same time interval 5, the D counts in energy bin 3 have to be as large as possible; (3) In energy bin 4 the counts have to be equal to zero (no signal expected); (4) for other time intervals (1 to 4), the number of counts between energy bins 1 to 3 has to show similar values between them (at least considering statistical fluctuations) and drop steeply in energy bin 4, as it is expected [38]. With these criteria the number of potential D centres was drastically reduced to 302.
The next limitation imposed to potential D centre locations is that the average of the D/H ratio in complete spring season, calculated without considering the D/H ratio measured in energy bin 3 in time interval 5 (because we expected that it is interstellar origin) is near to the terrestrial D/H ratio ∼1.5·10−4. This condition results in a reduction of the number of potential centre locations to 11.
The final constraint imposed was the counting of H and D signal along the ecliptic longitude should match the temporal behaviour observed for the H sputtering signal from interstellar He, i.e., the Gaussian-like curve (low at the flanks in time intervals 1 and 5, and maximum in time interval 3). This criterion reduced the number of potential centre locations to 3. Finally, we arrived at the deuterium peak centre in the 3-D TOF space that fulfils all the constraints listed above, This is located at 40.57 ns, 20.65 ns, and 23.21 ns for TOF0, TOF1, and TOF2, respectively (Figure 13).
The analytical results for the selected D centre locations will be shown in the next section. We have to notice that not necessarily the centre of the ellipsoid and some of expected position or a particular event of deuterium match, but the distance between the final three locations do not differ by more than 0.5 ns in each TOF dimension. Another remarkable issue is the size of D ellipsoid, which is of the order of 1 ns, and slightly less in the TOF0 axis. If we considerer this small volume for D counting, we are clearly not considering some of the real D events candidates, since we are working at the plus-minus one sigma level when collecting events, both for H and D. However, with the small collection volume we are fully removing the H tail. Those H ions that had just enough energy lost in the C-foil 1, thus to look like D events in TOF2, have a slightly different energy loss than D through the C-foil 2 and so will be outside the small collection ellipsoid.
The utility of the use of three dimensions TOF space and histogramming in two dimensions is evident: the mass equations give us an accurate position of the D peak, the analysis of the H tails allows to separate their contribution to the deuterium signal. Inspection of the 2D histogrammes gives an explanation for background observed in one dimension. Only the 3D analysis was successful to pick out and count the correct D events. Figure 14 shows a schematic representation of three dimensions TOF method.
3. Results and Discussion
We count the collected hydrogen and deuterium events for energy bins 1–4 and calculate the D/H ratio in each of five time interval of the spring passage. In the upper histogram of Figure 15 shows the H measurements for energy bins in each time interval, which have a shape similar to that observed in energy spectrum shown in Figure 3. This behaviour is expected since the H signal collected is from H sputtered by the interstellar He flux. Only in the last time interval the signal is a combination of the sputter H signal and the interstellar hydrogen. We subtracted the known sputtered H energy spectrum of the total signal to derive the interstellar H spectrum in the time interval 5 (same analysis as in [21]), which is indicated by the grey bars in Figure 15. The variation with time of the H signal (i.e., time interval 1 to 5) is given by the He flux variation as a function of ecliptic longitude, in a manner similar to the observed in Figure 4.
In the bottom histogram of Figure 15, the measurements of deuterium are displayed along the spring season. The entire D profile looks similar to the H data but with much lower count rate. For individual time intervals, the energy bins shown statistically similar to H spectral shape; the number of deuterium events in the three first energy bins has very similar values between them and in energy bin 4 shows few or no D signal at all. In time interval 5 the D counts in energy bins 1 and 2 follow the downward trend with ecliptic longitude as expected from the He sputtering (matching the shape of the interstellar He curve for the spring passage). Only for energy bin 3 in time interval 5 the D signal appears to be outside the general pattern for D being sputtered by interstellar He.
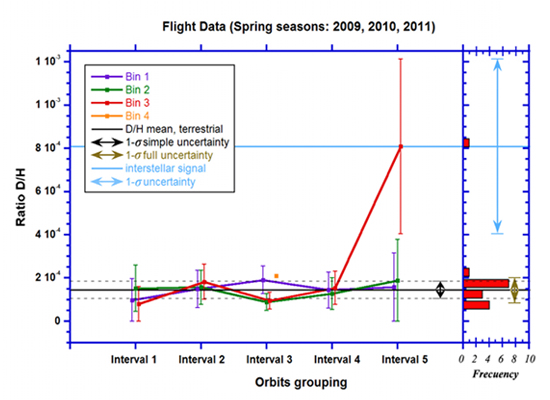
Based on the time dependence of the sputtered H signal from interstellar He, which we see also in the sputtered D signal, we estimate that 1 of the 4 counts of the D signal in energy bin 3 of time interval 5 should be attributed to the sputtered component (terrestrial D) and 3 counts are the true interstellar D signal. To validate this assignment we first calculate the D/H ratio taking a pessimistic assumption: the interstellar He sputtering product completely dominates the D and H signal during spring passage, including time interval 5. The D/H ratio then simply is the fraction of deuterium and hydrogen counts collected in the each energy bin: D/H = cts(D)/cts(H), represented by different coloured lines. Figure 16 shows the resulting D/H ratios derived for all energy bins (represented by different coloured lines) for each time interval. The errors bars give the statistical uncertainty of each measurement, detection uncertainties cancel out because ratios are single energy bin. The D/H ratios are found to be of the same value (within uncertainty) for all but one measurement. Only the D/H measurement for energy bin 3 at time interval 5 significantly deviates from the rest. This supports the assumption that it is of different origin, of interstellar origin, compared to the rest of the measurements. On the right-hand side of Figure 16 we plotted a frequency histogram, again supporting this conclusion. We calculated the average ratio D/H = (1.45 ± 0.93)·10−4 without the measurement of energy bin 3 in time interval 5, because of its assumed different origin compared to all the other measurements (its position is far away from the average, see Figure 16, right panel). This average D/H ratio is in good agreement with the terrestrial D/H value of (1.5576 ± 0.007)·10−4 (Vienna Standard Mean Ocean Water), and thus strongly supports the terrestrial origin (i.e., the sputter origin) of these D counts. The solid black line in Figure 16 represents the average measured D/H ratio, without the measurement of energy bin 3 in time interval 5. If we attribute 1 of the 4 observed D counts in energy bin 3 to sputtering of D by interstellar He, then the resulting D/H value is (2.02 ± 2.02)·10−4 for this single measurement, which agrees within the 1-sigma interval with the average D/H value for the other 15 D/H measurements.
In the following we assess the statistical significance of this measurement. Assuming the 6 deuterium counts at time interval 5 are Poisson distributed sputtered D, then the statistical probability for 4 counts in one of the three energy bins and a total six counts (Figure 15), i.e., for a μp = 6/3, is 9%. This means that the confidence for true detection of interstellar D in energy bin 3 is 91%. The probability for 0 counts in an energy bin in time interval 5 is 13%. The statistically significant excess of counts at energy step 3 in time interval 5 is strong evidence that these D atoms are of interstellar origin. We also can perform a similar counting statistics analysis for just energy bin 3 in time interval 5 (see the distribution in the right panel of Figure 16). Collecting four counts in this channel while the average due to sputtered terrestrial D is one or less results in a probability of less than 4%. This reasoning based solely on Poisson statistics for this energy bin and time interval can be taken as evidence that we have detected interstellar D with a better than 96% confidence level. Other possibility is developing a statistical hypothesis test. We propose two hypotheses, the null hypothesis, which assumes that all the events collected in energy bin 3 in time interval 5 are from sputtering H, and the alternative hypothesis which assumes that at least three of these events are from interstellar D. Using as expected mean and the standard deviation equal to one, the results of one sample two-tailed t-test to p-value or alpha (α) level is equals 0.0093 with a standard error of difference of 50%, this difference is considered to be statistically very significant, and the null hypothesis can be rejected. Figure 16, right panel, shows the histogram of all D/H measurements together with uncertainties: the simple uncertainty is the standard deviation of the D/H measurements and the full uncertainty considers also the uncertainty of the individual measurement for the combined uncertainty. By comparing the full uncertainty with the uncertainty of the measurement in energy bin 3 at time interval 5 we see that they are separated by 1-sigma.
In the three years of the IBEX mission time, the observation geometry and orbit allowed for a total observation time in time interval five (see Figure 4) of 115.3 days. However, the effects of the spinning spacecraft as well as the stepping through 8 energy channels mean that we are only observing the interstellar wind for a total time of 1.44 days, in which about ∼2 counts for interstellar deuterium are expected in time interval 5 [23].
To obtain the interstellar D/H ratio, we need to convert the interstellar D and interstellar H counts into physical fluxes, because interstellar D and H arrive at 1 AU with different energy, and thus in different energy bins. To first order, we can assume the same detection efficiency for D and H in IBEX-Lo, since the ionisation during the scattering from the conversion surface is an electronic process [33,42] and should not be affected by the heavier D nucleus. The good agreement, within error bars, of the D/H ratio for the sputtered signal with the terrestrial value supports this assumption. For the interstellar H flux we have to consider the counts in energy bin 1 and energy bin 2 (see Table 3), which are converted to a physical H flux using the IBEX-Lo calibration [43]. We arrive at D/H = (4.04 ± 2.75)·10−4 at 1 AU, where the statistical errors and the instrument calibration uncertainty have been considered. To refine this result, we take the difference between the terrestrial D/H and our measurement of the sputtered D/H to calibrate the detection efficiency for D based on the H measurement, in the absence of a laboratory calibration for D. Thus, we have to correct our measurement of the interstellar D/H with the factor 1.5576/1.45 = 1.075. This results in an interstellar D/H ratio of (4.34 ± 2.96)·10−4 at 1 AU. We have to apply an additional correction for the different viewing times of interstellar D and interstellar H in interval 5 (see Figure 4). The viewing time for interstellar H is derived from the measurements [21] as 95.7 %, and the viewing time for interstellar D is derived from the model by Kubiak et al. [23] as 38.6%. The resulting measurement D/H of LISM at 1 AU is D/H = (1.08 ± 0.73)·10−3.
4. Conclusions
We report on a comprehensive signal processing procedure for very low signal levels for the measurement of neutral species in the local interstellar medium from a spacecraft in Earth orbit. In to our earlier work [8], the 3D-TOF method demonstrated that deuterium from the local interstellar medium can be measured in the interstellar wind with IBEX-Lo at Earth orbit at a low signal level of counts-per-year. To reach this sensitivity we use a comprehensive signal processing software. In the present data analysis, which exploits the complete measurement capability of IBEX-Lo TOF sensor, we find 3 counts for interstellar deuterium.
The utility of use of a 3D-TOF analysis and histogramming the data in 2D is clear: the creation of the mass relation gives us an accurate D peak location, and the contributions of H-tails to the deuterium signal are separated, providing a reduction of observed background. Finally, the 3D analysis determines a useful method to counting D events. We can expect that this method will allow for the analysis of other low-level species in IBEX-Lo data without obvious peak in the 1D or 2D histogram data.
The present analysis was made with all IBEX-Lo data available for this investigation, i.e., with the data from the years 2009 through 2011. Although the deuterium signal is very weak, a clear signal was identified by the analysis method using three dimensional TOF space. Additional requirements to assure the correctness of the D signal were that the interstellar D signal was identified in the expected time interval (i.e., at the correct ecliptic longitude) and at the expected energy (in energy bin 3, at 55.5 eV centre energy). Moreover, the D signal we measure for the sputtered D signal from the interstellar He flux follows exactly the temporal evolution of the interstellar He signal, and shows the characteristic energy spectra for a sputtered signal. The measured D/H ratio for this terrestrial signal is in good agreement with the terrestrial D/H value, as expected, demonstrating the capability of IBEX-Lo to measure the D/H ratio.
We find for the interstellar deuterium a value of D/H = (1.08 ± 0.73)·10−3 at 1 AU, which is an update to our earlier value [8]. This D/H value at 1 AU can be transferred to the D/H value at the heliospheric termination shock at 100 AU by accounting for the transport and ionisation loss during the transit from the termination shock to Earth orbit [23], which gives D/H = (1.6 ± 1.0)·10−5. This value is equal to the LISM value if the filtration at the termination shock and the secondary populations for H and D in the heliosheath are the same. Our D/H value is consistent with the D/H ratio inferred by Hubble spectroscopy of a line of sight measurement of the LIC (1.6 ± 0.4)·10−5 [7]. The D/H ratio we measure for the interstellar signal at Earth orbit (1 AU) is also in good agreement with theoretical predictions by Tarnopolski and Bzowski [22] assuming a D/H value of 1.6·10−5 in the local interstellar medium.
Our present analysis has large uncertainty and is thus only of limited use for a detailed scientific discussion. It does demonstrate, however, that in situ measurements of interstellar D from the inner heliosphere are possible. For optimised IBEX-Lo observations, to be performed during the upcoming solar minimum period in about 2019, it is estimated that the detection of interstellar D with IBEX-Lo is improved by a factor of up to 10 [8], with a corresponding improvement in accuracy of the D/H ratio.
Acknowledgments
This work is supported by the Swiss National Science Foundation. M. Bzowski, M.A. Kubiak, and J.M. Sokół were supported by the Polish Ministry for Science and Higher Education grant N-N203-513-038, managed by the Polish National Science Center. The work by US authors was supported by the IBEX mission, which is funded as a part of NASA’s Explorer Program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McComas, D.J.; Allegrini, F.; Bochsler, P.; Bzowski, M.; Collier, M.; Fahr, H.; Fichtner, H.; Frisch, P.; Funsten, H.O.; Fuselier, S.A.; et al. IBEX interstellar boundary explorer. Sp. Sc. Rev 2009, 146, 11–33. [Google Scholar]
- Linsky, J.L. Atomic Deuterium/hydrogen in the galaxy. Sp. Sc. Rev 2003, 106, 49–60. [Google Scholar]
- Linsky, J.L. D/H nearby interstellar cloud structures. Sp. Sc. Rev 2007, 130, 367–375. [Google Scholar]
- Prodanovic, T.; Fields, B.D. FUSE deuterium observations: A strong case for galactic infall. J. Cosmol. Astropart. P 2008, 9, 003. [Google Scholar]
- Yuan, Y.; Neufeld, D.A.; Sonnentrucker, P.; Melnick, G.J.; Watson, D.M. Spitzer observations of shock-excited hydrogen deuteride in IC 443C, HH 7, and HH 54: Probing the gas-phase deuterium abundance in the dense interstellar medium. Astrophys. J 2012, 753, 126. [Google Scholar]
- Linsky, J.L.; Draine, B.T.; Moos, H.W.; Jenkins, E.B.; Wood, B.E.; Oliveira, C.; Blair, W.P.; Friedman, S.D.; Gry, C.; Knauth, D.; et al. What is the total deuterium abundance in the local galactic disk? Astrophys. J 2006, 647, 1106–1124. [Google Scholar]
- Hébrard, G.; Mallouris, C.; Ferlet, R.; Koester, D.; Lemoine, M.; Vidal-Madjar, A.; York, D. Ultraviolet observations of Sirius A and Sirius B with HST-GHRS. An interstellar cloud with a possible low deuterium abundance. Astron. Astrophys 1999, 350, 643–658. [Google Scholar]
- Rodríguez, M.D.F.; Wurz, P.; Saul, L.; Bzowski, M.; Kubiak, M.A.; Sokół, J.M.; Frisch, P.; Fuselier, S.A.; McComas, D.J.; Möbius, E.; et al. Evidence for direct detection of interstellar deuterium in the Local Interstellar Medium by IBEX. Astron. Astrophys 2013, 557, 125. [Google Scholar]
- Frisch, P.C.; Redfield, S.; Slavin, J.D. The interstellar medium surrounding the sun. Annu. Rev. Astron. Astr 2011, 49, 237–279. [Google Scholar]
- McComas, D.J.; Alexashov, D.; Bzowski, M.; Fahr, H.; Heerikhuisen, J.; Izmodenov, V.; Lee, M.A.; Möbius, E.; Pogorelov, N.; Schwadron, N.A.; et al. The Heliosphere’s interstellar interaction: No bow shock. Science 2012, 336, 1291–1293. [Google Scholar]
- Slavin, J.D.; Frisch, P.C. The boundary conditions of the heliosphere: Photoionization models constrained by interstellar and in situ data. Astron. Astrophys 2008, 491, 53–68. [Google Scholar]
- Baranov, V.B.; Malama, Y.G. Model of the solar wind interaction with the local interstellar medium—Numerical solution of self-consistent problem. J. Geophys. Res 1993, 98, 15157–15163. [Google Scholar]
- Müller, H.R.; Frisch, P.C.; Florinski, V.; Zank, G.P. Heliospheric response to different possible interstellar environments. Astrophys. J 2006, 647, 1491–1505. [Google Scholar]
- Fahr, H.J. Change of interstellar gas parameters in stellar-wind-dominated astrospheres: Solar case. Astron. Astrophys 1978, 66, 103–117. [Google Scholar]
- Fahr, H.J. Interstellar hydrogen subject to a net repulsive solar force field. Astron. Astrophys 1979, 77, 101–109. [Google Scholar]
- Bzowski, M.; Sokół, J.M.; Tokumaru, M.; Fujiki, K.; Quémerais, E.; Lallement, R.; Ferron, S.; Bochsler, P.; McComas, D.J. Solar Parameters for Modelling the Interplanetary Background. In Cross-Calibration of Past and Present Far UV Spectra of Solar System Objects and the Heliosphere, ISSI Scientific Report Series 13; Bonnet, R.M., Quémerais, E., Snow, M., Eds.; Springer Science + Business Media: New York, NY, USA, 2013; Chapter 3; pp. 67–138. [Google Scholar]
- Bzowski, M.; Sokół, J.M.; Kubiak, M.A.; Kucharek, H. Modulation of neutral interstellar He, Ne, O in the heliosphere. Survival probabilities and abundances at IBEX. Astron. Astrophys 2013, 557, A50. [Google Scholar]
- McMullin, D.R.; Bzowski, M.; Möbius, E.; Pauluhn, A.; Skoug, R.; Thompson, W.T.; Witte, M.; von Steiger, R.; Ruciński, D.; Judge, D.; et al. Coordinated observation of local interstellar helium in the heliosphere: Heliospheric conditions that affect the interstellar gas inside the heliosphere. Astron. Astrophys 2004, 426, 885–895. [Google Scholar]
- Ruciński, D.; Cummings, A.C.; Gloeckler, G.; Lazarus, A.J.; Möbius, E.; Witte, M. Ionization processes in the heliosphere. Rates and methods of their determination. Sp. Sc. Rev 1996, 78, 73–84. [Google Scholar]
- Ruciński, D.; Fahr, H.J. The influence of electron impact ionization on the distribution of interstellar helium in the inner heliosphere; possible consequences for determination of interstellar helium parameters. Astron. Astrophys 1989, 224, 290–298. [Google Scholar]
- Saul, L.; Wurz, P.; Rodriguez, D.; Scheer, J.; Möbius, E.; Schwadron, N.; Kucharek, H.; Leonard, T.; Bzowski, M.; Fuselier, S.; et al. Local interstellar neutral hydrogen sampled in situ by IBEX. Astrophys. J. Suppl. S 2012, 198, 14. [Google Scholar]
- Tarnopolski, S.; Bzowski, M. Detectability of neutral interstellar deuterium by a forthcoming SMEX mission IBEX. Astron. Astrophys 2008, 483, L35–L38. [Google Scholar]
- Kubiak, M.A.; Bzowski, M.; Sokół, J.M.; Möbius, E.; Rodriguez, D.F.; Wurz, P.; McComas, D.J. Assessment of detectability of neutral interstellar deuterium by IBEX observations. Astron. Astrophys 2013, 556, A39. [Google Scholar]
- McComas, D.; Allegrini, F.; Bochsler, P.; Bzowski, M.; Collier, M.; Fahr, H.; Fichtner, H.; Frisch, P.; Funsten, H.; Fuselier, S. The Interstellar Boundary Explorer (IBEX). In Aip Conference Proceedings, Proceedings of the 3rd International Conference of the Institute-of-Geophysics-and-Planetary-Physics, February 2004; University California Riverside: Riverside, CA, USA.
- Funsten, H.O.; Allegrini, F.; Crew, G.B.; de Majistre, R.; Frisch, P.C.; Fuselier, S.A.; Gruntman, M.; Janzen, P.; McComas, D.J.; Möbius, E.; et al. Structures and spectral variations of the outer heliosphere in ibex energetic neutral atom maps. Science 2009, 326, 964–966. [Google Scholar]
- Fuselier, S.A.; Allegrini, F.; Funsten, H.O.; Ghielmetti, A.G.; Heirtzler, D.; Kucharek, H.; Lennartsson, O.W.; McComas, D.J.; Möbius, E.; Moore, T.E.; et al. Width and variation of the ENA flux ribbon observed by the interstellar boundary explorer. Science 2009, 326, 962–964. [Google Scholar]
- McComas, D.J.; Allegrini, F.; Bochsler, P.; Bzowski, M.; Christian, E.R.; Crew, G.B.; DeMajistre, R.; Fahr, H.; Fichtner, H.; Frisch, P.C.; et al. Global observations of the interstellar interaction from the interstellar boundary explorer (IBEX). Science 2009, 326, 959–962. [Google Scholar]
- Schwadron, N.A.; Bzowski, M.; Crew, G.B.; Gruntman, M.; Fahr, H.; Fichtner, H.; Frisch, P.C.; Funsten, H.O.; Fuselier, S.; Heerikhuisen, J.; et al. Comparison of interstellar boundary explorer observations with 3D global heliospheric models. Science 2009, 326, 966–968. [Google Scholar]
- Fuselier, S.A.; Bochsler, P.; Chornay, D.; Clark, G.; Crew, G.B.; Dunn, G.; Ellis, S.; Friedmann, T.; Funsten, H.O.; Ghielmetti, A.G.; et al. The IBEX-Lo sensor. Sp. Sc. Rev 2009, 146, 117–147. [Google Scholar]
- Funsten, H.O.; Allegrini, F.; Bochsler, P.; Dunn, G.; Ellis, S.; Everett, D.; Fagan, M.J.; Fuselier, S.A.; Granoff, M.; Gruntman, M.; et al. The interstellar boundary explorer high energy (IBEX-Hi) neutral atom imager. Sp. Sc. Rev 2009, 146, 75–103. [Google Scholar]
- Wurz, P.; Fuselier, S.A.; Möbius, E.; Funsten, H.O.; Brandt, P.C.; Allegrini, F.; Ghielmetti, A.G.; Harper, R.; Hertzberg, E.; Janzen, P.; et al. IBEX backgrounds and signal-to-noise ratio. Sp. Sc. Rev 2009, 146, 173–206. [Google Scholar]
- Wieser, M.; Wurz, P.; Möbius, E.; Fuselier, S.A.; Hertzberg, E.; McComas, D.J. The ion-optical prototype of the low energy neutral atom sensor of the Interstellar Boundary Explorer Mission (IBEX). Rev. Sci. Instrum 2007, 78, 124502. [Google Scholar]
- Wurz, P. Detection of Energetic Neutral Atoms. In The Outer Heliosphere: Beyond the Planets; Scherer, K., Fichtner, H., Marsch, E., Eds.; Copernicus Gesellschafte. V.: Katlenburg-Lindau, Germany, 2000. [Google Scholar]
- Möbius, E.; Kucharek, H.; Granoff, M.; King, B.; Longworth, S.; Saul, L.; Fuselier, S.; Hertzberg, E.; Livi, S.; Paschalidis, N.; et al. Time-of-Flight Detector System with Low Background Performance for the IBEX-Lo Sensor. In AGU Fall Meeting Abstracts, Proceedings of the 30th International Cosmic Ray Conference, Mérida, Yucatán, Mexico, July 2007; Caballero, R., D’Olivo, J.C., Medina-Tanco, G., Nellen, L., Sánchez, F.A., Valdés-Galicia, J.F., Eds.; Universidad Nacional Autónoma de México, México, México, 2008; Volumen 1,. pp. 841–844. [Google Scholar]
- Möbius, E.; Kucharek, H.; Clark, G.; O’Neill, M.; Petersen, L.; Bzowski, M.; Saul, L.; Wurz, P.; Fuselier, S.A.; Izmodenov, V.V.; et al. Diagnosingthe neutral interstellar gas flow at 1 AU with IBEX-Lo. Sp. Sc. Rev 2009, 146, 149–172. [Google Scholar]
- Wurz, P.; Saul, L.; Scheer, J.A.; Möbius, E.; Kucharek, H.; Fuselier, S.A. Negative helium generation upon surface scattering: Application in space science. J. Appl. Phys 2008, 103, 054904. [Google Scholar]
- Möbius, E.; Bochsler, P.; Bzowski, M.; Heirtzler, D.; Kubiak, M.A.; Kucharek, H.; Lee, M.A.; Leonard, T.; Schwadron, N.A.; Wu, X.; et al. Interstellar gas flow parameters derived from interstellar boundary explorer-Lo observations in 2009 and 2010: Analytical analysis. Astrophys. J. Suppl. S 2012, 198, 11. [Google Scholar]
- Saul, L.; Bzowski, M.; Fuselier, S.; Kubiak, M.; McComas, D.; Möbius, E.; Sokól, J.; Rodriguez, D.; Scheer, J.; Wurz, P. Local interstellar hydrogen’s disappearance at 1 AU: Four years of IBEX in the rising solar cycle. Astrophys. J 2013, 767, 130. [Google Scholar]
- Bochsler, P.; Petersen, L.; Möbius, E.; Schwadron, N.A.; Wurz, P.; Scheer, J.A.; Fuselier, S.A; McComas, D.J.; Bzowski, M.; Frisch, P.C. Estimation of the Neon/Oxygen abundance ratio at the heliospheric termination shock and in the local interstellar medium from IBEX observations. Astrophys. J. Suppl. S 2012, 198, 13. [Google Scholar]
- Beiersdorfer, P.; Roquemore, A.L.; Kaita, R. Characteristics of compact solid-target charge exchange analyzers for energetic ion diagnostics on tokamaks. Rev. Sci. Instrum 1987, 58, 2092–2098. [Google Scholar]
- Mikheev, S.; Ryzhov, Y.; Shkarban, I.; Yurasova, V. Inelastic losses of low-energy ions transmitted through thin films. Nucl. Instrum. Meth. B 1993, 78, 86–90. [Google Scholar]
- Wurz, P.; Wieser, M.E; Scheer, J.A. Particle scattering off surfaces: Application in space science. eJSSNT 2006, 4, 394–400. [Google Scholar]
- Rodriguez, M.D.F.; Saul, L.; Wurz, P; Fuselier, S.A.; Funsten, H.O.; McComas, D.J.; Möbius, E. IBEX-Lo observations of energetic neutral hydrogen atoms originating from the lunar surface. Planet. Sp. Sci 2012, 60, 297–303. [Google Scholar]
















| Year | January | February | March | April | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 108 | 109 | 111 | 112 | 113 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | ||
| 2010 | 60 | 61 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | |
| 2009 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Ecliptic Long. [°] | 283 | 291 | 298 | 306 | 313 | 321 | 329 | 336 | 344 | 351 | 359 | 7 | 14 | 22 |
| Time Interval | 1 | 2 | 3 | 4 | 5 | |||||||||
| Species | H | mass = 2 | He | C | O | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tech | EMG | MEQ | EMG | MEQ | EMG | MEQ | EMG | MEQ | EMG | MEQ |
| TOF0 | 29.525 | 29.331 | - | 42.416 | - | 59.854 | 119.196 | 119.145 | 135.945 | 136.074 |
| TOF1 | 13.935 | 14.108 | - | 21.656 | - | 30.869 | 59.721 | 59.698 | 67.513 | 67.574 |
| TOF2 | 14.467 | 14.339 | - | 22.228 | - | 31.604 | 60.298 | 60.276 | 67.960 | 68.020 |
| H | D | D/H | |
|---|---|---|---|
| He sputtering all cases from Figure 16 | / | / | (1.45 ± 0.93)·10–4 |
| Terrestrial | / | / | (1.5576 ± 0.007)·10–4 Vienna Standard Mean Ocean Water |
| LISM at 1 AU | 2747 cts time interval 5 energy bin 1 1027 cts time interval 5 energy bin 2 | 4 cts time interval 5 energy bin 3 * 3 cts LISM 1 ct sputtering | (4.04± 2.75)·10–4 |
| LISM at 1 AU with correction for efficiency | / | / | (4.34 ± 2.96)·10–4 |
| LISM at 1 AU with correction for viewing time | / | / | (1.08 ± 0.73)·10–4 |
| LISM at TS | / | / | (1.6 ± 1.0)·10–3 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rodríguez Moreno, D.F.; Wurz, P.; Saul, L.; Bzowski, M.; Kubiak, M.A.; Sokół, J.M.; Frisch, P.; Fuselier, S.A.; McComas, D.J.; Möbius, E.; et al. Signal Processing for the Measurement of the Deuterium/Hydrogen Ratio in the Local Interstellar Medium. Entropy 2014, 16, 1134-1168. https://doi.org/10.3390/e16021134
Rodríguez Moreno DF, Wurz P, Saul L, Bzowski M, Kubiak MA, Sokół JM, Frisch P, Fuselier SA, McComas DJ, Möbius E, et al. Signal Processing for the Measurement of the Deuterium/Hydrogen Ratio in the Local Interstellar Medium. Entropy. 2014; 16(2):1134-1168. https://doi.org/10.3390/e16021134
Chicago/Turabian StyleRodríguez Moreno, Diego Francisco, Peter Wurz, Lukas Saul, Maciej Bzowski, Marzena Aleksanda Kubiak, Justyna Maria Sokół, Priscilla Frisch, Stephen Anthony Fuselier, David John McComas, Eberhard Möbius, and et al. 2014. "Signal Processing for the Measurement of the Deuterium/Hydrogen Ratio in the Local Interstellar Medium" Entropy 16, no. 2: 1134-1168. https://doi.org/10.3390/e16021134
APA StyleRodríguez Moreno, D. F., Wurz, P., Saul, L., Bzowski, M., Kubiak, M. A., Sokół, J. M., Frisch, P., Fuselier, S. A., McComas, D. J., Möbius, E., & Schwadron, N. (2014). Signal Processing for the Measurement of the Deuterium/Hydrogen Ratio in the Local Interstellar Medium. Entropy, 16(2), 1134-1168. https://doi.org/10.3390/e16021134