Dynamics and Thermodynamics of Nanoclusters

Abstract

The dynamic and thermodynamic properties of nanoclusters are studied in two different environments: the canonical and microcanonical ensembles. A comparison is made to thermodynamic properties of the bulk. It is shown that consistent and reproducible results on nanoclusters can only be obtained in the canonical ensemble. Nanoclusters in the microcanonical ensemble are trapped systems, and inconsistencies will be found if thermodynamic formalism is applied. An analytical model is given for the energy dependence of the phase space volume of nanoclusters, which allows the prediction of both dynamical and thermodynamical properties.

1. Introduction

Nanoclusters are small finite systems consisting of from several atoms to several thousands of atoms. These systems are interesting because their physical, optical and electronic characteristics are strongly size dependent. Often changing the size by only one atom can significantly alter the physical-chemical properties of the system. Many new periodic tables can thus be envisioned in which differently-sized clusters of the same material become the new elements. Potential applications are enormous, ranging from devices in nano-electronics and nano-optics [1] to applications in medicine and materials. A revolution in technology based on nanoclusters is at the point of fruition, predicted to be on a scale as large, or larger, than either the industrial or digital revolutions.

However, before the engineering of new designs and devices can be contemplated, complete physical characterization of nanoclusters is needed. Of particular importance is the understanding of the dynamic and thermodynamic behavior of these systems in different environments [2,3,4,5,6].

The present article studies the dynamics and thermodynamics of nanoclusters in two different environments, the microcanonical and canonical ensembles. It will become clear that the choice of the environment, or ensemble, in which the thermodynamic properties of the nanocluster are to be determined is crucial, since they generally lead to different, and therefore inconsistent, results. This is because in the microcanonical ensemble, nanoclusters inevitably become trapped at low energy in only a sub-region of the energetically-available phase space, and so, the system never arrives at a true thermodynamic equilibrium, independently of the amount of time allowed for convergence. Consistent and reproducible thermodynamic results cannot therefore be expected, and any results so obtained will depend on initial conditions or subsequent perturbation. However, under some circumstances, and under the premise that the initial conditions can be ascertained, dynamical information obtained in the microcanonical ensemble may be useful in describing the behavior of nanoclusters in a given practical application.

The work presented in this paper concerning the trapping by large energy barriers has relevance not only to nanoclusters, but to all “small” systems, in which the size of the system is small with respect to the range of the inter-particle forces. This occurs for any size of system if the inter-particle potentials decay with exponents smaller than the dimensionality of the embedding space, for example in the case of self-gravitating systems. In these cases, the time “relaxed” distributions will be very dependent on initial conditions [7]. Since these systems can never obtain thermodynamic equilibrium, the application of the thermodynamic formalism to these systems is unjustified and will lead to inconsistencies in the formalism, including the apparent violation of fundamental law and negative heat capacities [8,9].

The canonical ensemble is more suited to obtaining reproducible thermodynamic information, which is independent of the initial condition or subsequent perturbation in the time-relaxed state. This is because in the canonical ensemble, the nanoclusters’ environment is a thermal reservoir, which allows the exchange of energy, permitting the cluster to pass energy barriers and thereby visit all of its available phase space, at least in principle. However, even in the canonical ensemble, caution must be exercised before assuming thermodynamic equilibrium. Energy barriers between different isomeric forms (between solid-solid or between solid and mixed solid-liquid forms) of the nanocluster can be very high. Surmounting them can take excessively large times that are impractical to be simulated in numerical experiments or observed in real experimental conditions.

This situation, whether in the microcanonical or canonical ensembles, has been conceptualized as broken ergodicity and has been a constant source of confusion, stimulating much heated debate within the nanocluster community [4,10,11,12,13].

Applying the equilibrium thermodynamic formalism to a system trapped out of equilibrium will lead to inconsistencies and paradoxes with the postulates and theorems of the thermodynamic formalism [14]. One of these inconsistencies has been the reporting of the so-called “negative heat capacity”, resulting from the a priori presumption of the validity of the results of the thermodynamic formalism obtained in the microcanonical ensemble.

The basic ergodicity hypothesis of molecular simulation ensures that thermodynamic results are equal in the microcanonical and canonical ensembles if the simulation is ergodic and well converged. The difference between results obtained in the canonical and microcanonical ensembles leads some researchers to conjecture the existence of two thermodynamics for small systems [5,8]. Our stance regarding this controversy has been to emphasize that nanoclusters in the microcanonical ensemble are not systems that can reach thermodynamic equilibrium, and therefore, it is inconsistent to apply the equilibrium thermodynamic formalism to such systems [4]. An important conclusion that came out of this previous work was that, since all macroscopic results obtained on systems trapped out of equilibrium will depend on the initial conditions (which, for nanoclusters, still cannot be adequately controlled in the laboratory) or depend on subsequent perturbation, many published results on nanocluster thermodynamics should be carefully re-examined.

The focus of our present study of the thermodynamic properties of nanoclusters will be the caloric curve, and thus, we first describe the anatomy of this curve in detail in Section 2. In Section 3, we emphasize the differences to be expected for this curve between that obtained on material in the bulk and that obtained on nanoclusters. In Section 4, we mention the frequent, but false assumptions and caveats normally encountered in the literature on the thermodynamics of nanoclusters. In Section 5, we present a simple model for obtaining the energy dependence of the density of states of a nanocluster in true thermodynamic equilibrium. This density of states can only be correctly obtained in the canonical (or macrocanonical) ensemble, since trapping in the microcanonical ensemble is inevitable. In the same section, we consider a modification of our model for the thermodynamics that allows us to include energy barriers and, thus, to simulate what would be expected in the microcanonical ensemble for particular initial conditions. This allows initial condition-dependent dynamical information to be obtained for the system. A comparison is then made of our results with caloric curves and heat capacities obtained using molecular dynamics at constant energy (the microcanonical ensemble). Section 6 presents a discussion and conclusions.

2. The Anatomy of a Caloric Curve

The caloric curve is the graph of the temperature of a system as a function of its internal energy. The temperature is defined as the inverse of the partial derivative of the entropy with respect to energy at constant particle number and constant volume: $T={\left(\frac{\partial S}{\partial E}\right)}_{V,N}^{-1}$. It is thus an inverse measure of how fast the entropy is increasing with respect to the energy; if the entropy increases slowly with energy, the temperature is high, and vice versa. At the melting energy of the cluster, the caloric curve may demonstrate an inflection, which is due to the sudden increase in the number of modes for storing energy as the cluster becomes liquid (atoms in the liquid can carry translational and rotational kinetic energy related to their diffusion within the volume). Figure 1 shows a typical caloric curve for a nanocluster demonstrating a phase transition at an energy of 7.5 eV.

Figure 1. Example of a caloric curve, for a nanocluster.

Figure 1. Example of a caloric curve, for a nanocluster.

The heat capacity is the inverse slope of the caloric curve, $C_{V,N}={\left(\frac{\partial T}{\partial E}\right)}_{V,N}^{-1}$, and is thus an inverse measure of how fast the temperature is changing with energy; if the temperature increases slowly with energy, the heat capacity is high, and vice versa.

For a cluster of N atoms, which is neither rotating nor translating (angular and linear momentum fixed at zero), there are only 3N − 6 normal vibrational degrees of freedom. Each vibrational degree of freedom contributes two modes for storing energy; one in the kinetic energy associated with vibration and one in the potential energy (these are the two quadratic terms that enter the Hamiltonian for the solid). Each of these contributes 1/2k_B to the heat capacity (assuming that the energy is high enough to excite all vibrational modes). The heat capacity of the solid is thus (3N − 6)k_B, the Dulong–Petit law, and the slope before the transition (where the system is solid) is therefore 1/(3N − 6)k_B. This slope before the transition is practically the same for both the nanocluster and for the bulk. Note that the contribution to the slope of the caloric curve before the transition is the same for whatever symmetry (isomeric form) in which the cluster or bulk may be. This is simply because there are always only 3N − 6 vibrational degrees of freedom. (It is convenient to point out, however, that, if at low energies, not all vibrational modes can be excited or if strong anharmonicities in the potential are relevant, then the slope of the caloric curve before the transition may, in general, differ from the Dulong–Petit law.) The energy intercept of the caloric curve can be different, however, depending on the binding energy of the particular symmetry.

Approaching in energy from below the solid-to-liquid transition, the slope of the caloric curve for a nanocluster decreases (the heat capacity increases) because new modes for storing energy come into play. These modes are related to the fact that the surface atoms are now relatively free to move over the surface of the underlying solid structure and, thus, can carry energy in their translational modes on the two-dimensional surface of the structure. The 3N − 6 vibrational degrees of freedom remain even though they take on a lower frequency and generally become anharmonic. Each of these new translational modes contributes a further 1/2k_B to the heat capacity, and thus, the heat capacity increases as (3N − 6 + i)k_B, where i is the number of atoms in the liquid (the cluster may be a mixed solid and liquid).

The heat capacity can also be written in terms of the entropy as the second partial derivative of the entropy with respect to energy divided by the rate of change of entropy with energy (at constant volume and particle number),

$$C_{V,N}(E)={\left(\frac{{\partial }^{2}S}{\partial E^2}\right)}_{V,N}/{\left(\frac{\partial S}{\partial E}\right)}_{V,N}$$

(1)

It is also possible to write the heat capacity in terms of the phase space volume (or density of states) Γ(E) using Equation (1) and the Boltzmann equation, S(E) = k_B lnΓ(E). This gives,

$$C_{V,N}(E)={\left[1-\frac{\mathrm{\Gamma }(E){\mathrm{\Gamma }}^{″}(E)}{{\mathrm{\Gamma }}^{\prime }{(E)}^2}\right]}^{-1}$$

(2)

The heat capacity thus depends not only on the phase space volume Γ, but also on its first and second derivatives with respect to energy, ${\mathrm{\Gamma }}^{\prime }\equiv \partial \mathrm{\Gamma }/\partial E$ and ${\mathrm{\Gamma }}^{″}\equiv {\partial }^2\mathrm{\Gamma }/\partial E^2$ (at constant volume V and particle number N).

From Equation (2), we note that for the heat capacity to go negative, it is required that ΓΓ′′/Γ′ > 1. Such a change in the phase space volume will be referred to as “abrupt” in the following. Borrowing from the language of cosmology, one could say that the heat capacity goes negative when the phase space inflation, defined as ΓΓ′′/Γ′², becomes greater than unity. It can be ascertained that this will happen only if the phase space volume Γ increases faster than a power law or, more exactly, faster than a non-infinite sum of power laws, with energy [4]. However, quantization of the extensive variables prohibits the existence of such systems in nature (see [15] and the Discussion and Conclusions section of this paper).

3. Bulk versus Nanocluster Thermodynamics

The microstates contributing to the thermodynamics of bulk material (containing over 10²³ atoms) are overwhelmingly determined by the atoms of the volume. Except for particular processes, such as, for example, the initiation of melting, surface atoms play very little part in the thermodynamics, simply because there are too few surface atoms as compared to the vast amount of atoms of the bulk. Although a given bulk material may have a number of possible symmetries (e.g., fcc, bcc, hcp, etc.) these symmetries are separated from one another in state space by very large energy barriers that can only be surmounted at the melting temperature (the phase transition). At the energy of melting for the bulk, in the microcanonical ensemble, many new modes for storing energy become simultaneously accessible, and the phase space increases instantaneously, leading to a singularity in the caloric curve, which takes the form of a delta function. This leads to a discontinuous increase in the entropy and is the description of a first order phase transition.

Below the transition energy in bulk materials, not all microstates have a priori equal probability because there exists other symmetries corresponding to phase space regions that are never sampled because of the enormously large energy barriers between symmetries. However, for all practical purposes, before the transition, the other symmetries of the bulk can be safely ignored, and we can consider the system as having obtained thermodynamic “equilibrium” while existing in only one particular symmetry. This holds for both the microcanonical and canonical ensembles.

Different symmetries of the same material below the melting transition are named differently (e.g., graphite and diamond), and the caloric curve and all other thermodynamic results for a given symmetry are always reproducible, because the initial condition is easily determined and the same from one experiment to the next.

The thermodynamics of nanoclusters is different from that of the bulk precisely because the number of surface atoms is greater than, or of the order of, the number of volume atoms. The surface atoms have lower coordination (fewer nearest neighbors) and are thus less bound to the rest of the cluster. This fact, coupled with the finite size of the system, often implies that the different symmetries available to the cluster are separated from each other by barriers that can be below the melting energy. Solid to solid transitions are thus allowed before the melting transition [16], a possibility generally not available to the bulk.

The finite size of the system also means that new, additional, symmetries (for example, the icosahedra and decahedral) are allowed for the nanocluster, while they are strictly forbidden for the bulk. Furthermore, because nanoclusters are very small systems, thermodynamic averages (macroscopic results) imply that measurement must be made on an ensemble of identical systems. It is currently impossible experimentally to be able to control the initial conditions, and so, the distributions of the clusters among their many allowed symmetries will depend very much on the non-equilibrium process used to form them.

Since it is not possible to control initial conditions and, furthermore, since each member of the ensemble can change symmetry even before the phase transition energy, the only way to obtain useful (reproducible) information concerning the behavior of nanoclusters is to assure that one has a true thermodynamic equilibrium distribution over all symmetries at all energies. This, because of trapping by barriers, can only be obtained by employing a canonical ensemble in which energy can be utilized from the thermal reservoir to surmount the barriers.

Thus, for a nanocluster, different symmetries can come into play at total energies below the solid to liquid transition, and this is due to a combination of factors involving the total binding energy and the configurational and vibrational entropies of the cluster, as well as the structure and strength of the bonds of the outer layers. The phase space volume of a cluster thus increases more gradually near the transition than does that of the bulk, and there exists no singularity, but rather, an extended region in energy over which the heat capacity gradually increases as the system gains new modes for storing energy. These modes for storing energy are related to the fact that the atoms in the liquid are no longer constrained to particular symmetries, but are relatively free to pass over barriers and, so, can carry kinetic energy of diffusion over the two-dimensional surface of the underlying solid part of the cluster.

However, it is not always true that the energy barriers between different symmetries are below the solid to liquid transition energy. In Figure 2, we show that the energy barriers (blue, online, or dashed lines, in print) between the icosahedral (red, online, or dark grey, in print) and decahedral (green, online, or light grey, in print) isomers for the nanocluster Na₁₄₇ are large and, in fact, reach up to the energy (≈7.8 eV) of the transition region. Note, however, that in a truly equilibrium distribution, the microstates corresponding to the decahedral isomers should be accounted for at an energy of ≈0.8 eV, which is well below the barrier energy of ≈7.8 eV.

Figure 2. Plot showing the heights of the energy barriers (blue, online, or dashed lines, in print) between various isomers of the icosahedral (red, online, or dark grey, in print) and decahedral (green, online, or light grey, in print) isomers of Na₁₄₇. The red (dark grey, in print) lines mark the energy barriers between different isomers of icosahedral symmetry while the green (light grey, in print) lines mark the energy barriers between different isomers of decahedral symmetry. Data were obtained using a genetic algorithm to search the Gupta potential energy surface. Details are given in [17].

Figure 2. Plot showing the heights of the energy barriers (blue, online, or dashed lines, in print) between various isomers of the icosahedral (red, online, or dark grey, in print) and decahedral (green, online, or light grey, in print) isomers of Na₁₄₇. The red (dark grey, in print) lines mark the energy barriers between different isomers of icosahedral symmetry while the green (light grey, in print) lines mark the energy barriers between different isomers of decahedral symmetry. Data were obtained using a genetic algorithm to search the Gupta potential energy surface. Details are given in [17].

4. Frequent Caveats Encountered in the Analysis of the Thermodynamics of Nanoclusters

As mentioned above, the facts that clusters can become easily trapped in different symmetries, that this trapping is a function of energy and that initial conditions cannot be adequately controlled are at the origin of the inconsistencies found in the application of the equilibrium thermodynamic formalism to determine the thermodynamic properties of atomic nanoclusters.

The energy barriers between different isomers of the same symmetry are usually small, while those between isomers of different symmetry are large and often reach into, or beyond, the transition region (see Figure 2). For sufficiently low energy in the microcanonical ensemble, each cluster of the ensemble, just as in the case for the bulk, is trapped in one particular symmetry, which depends on its initial condition. However, unlike in the case of the bulk, the cluster may leave that particular symmetry of its initial condition before reaching the transition energy. 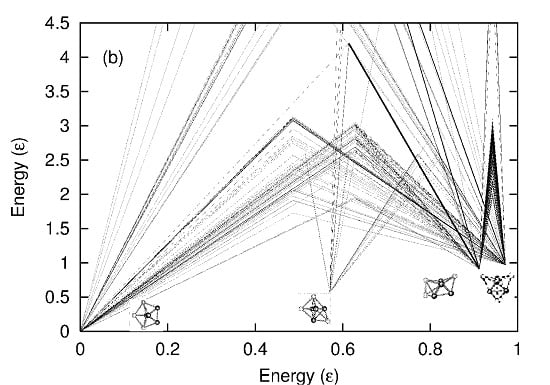As a specific example, Figure 3 demonstrates this “untrapping” of isomers before the transition for LJ₇ (a cluster of seven Lennard–Jones potential bound atoms). The figure shows the “caloric curves” obtained in the microcanonical ensemble (at constant energy) by starting the molecular dynamic simulations from the four different isomers of LJ₇, whose geometry is shown in the inset of the figure. From the figure, it can be ascertained that below an energy of 1.5 in units of ε (ε is the depth of the potential well for binary interaction), the cluster is trapped in the particular isomer defined by its initial condition. Hence, four distinct caloric curves are obtained on increasing the total energy, each corresponding to a different initial condition or isomer. Untrapping occurs at 1.5 ε, which is considerably lower than the transition energy of 3.5 ε.

Figure 3. (a) Four different caloric curves are obtained for LJ₇ by starting constant energy molecular dynamics simulations in the different isomers shown in the inset. This dependence on initial condition highlights the unavoidable trapping in the microcanonical ensemble. (b) Energy barriers between the different isomers obtained through a genetic algorithm search on the potential energy landscape, described in [17]. The barriers found in (b), the lowest at 1.5 ε, are in agreement with the results obtained in (a).

Figure 3. (a) Four different caloric curves are obtained for LJ₇ by starting constant energy molecular dynamics simulations in the different isomers shown in the inset. This dependence on initial condition highlights the unavoidable trapping in the microcanonical ensemble. (b) Energy barriers between the different isomers obtained through a genetic algorithm search on the potential energy landscape, described in [17]. The barriers found in (b), the lowest at 1.5 ε, are in agreement with the results obtained in (a).

For larger-sized clusters, the energy barriers between the different symmetries become higher and move closer in energy to the transition region. For larger systems, there is also the possibility of new microstates corresponding to part of the cluster in the solid phase and part of the same cluster in the liquid phase (referred to as phase separation in the literature). These states may include one, two, three, etc., up to all N atoms in the liquid.

It has often been assumed that these mixed solid-liquid states do not contribute to the thermodynamics below the transition energy, as it was argued that an energy cost of a presumed interface between the solid and liquid had to be paid [6]. The nature of the interface, however, was never explained nor investigated in the subsequent literature. The only support for this hypothesis was the observation that only rarely were mixed solid liquid states found in Monte Carlo and molecular dynamics simulations of clusters. These mixed states were, therefore, hitherto, not given their proper consideration in the thermodynamic analysis of clusters.

Our interpretation, however, is that these states were rarely observed, not due to their high energy, but instead because of the high energy barriers separating them from other regions of the space of available states. The heights of the energy barriers separating these mixed solid-liquid states from the solid states depend not only on how many atoms are in the liquid, but also on the nature of the symmetry of the underlying solid structure. For a large enough nanocluster in the microcanonical ensemble, these mixed solid-liquid states will be hidden from the simulation or experiment until surmounting their particular energy barriers. For the case of the magic number clusters (corresponding to closed geometry shells of a given symmetry), the barriers separating the mixed states from the solid states may be higher than the barrier between all solid and all liquid states (even though the mixed states are available, but not accessible at a significantly lower energy than all of the liquid states). Therefore, in the microcanonical ensemble, increasing the energy of the cluster may lead to a direct jump from the all-solid (or nearly all solid) to the all-liquid (or nearly all liquid) states. In this case, the measured phase space inflation may become so large that the apparent heat capacity, as determined by Equation (2), may become negative. We emphasize, however, that what is being measured is not a true heat capacity, since the system is not in thermodynamic equilibrium in the microcanonical ensemble because of trapping. The mixed solid-liquid states are hidden by the large energy barriers, but must be accounted for in an equilibrium calculation. Exactly how all this comes about and leads to the erroneous determination of “negative heat capacity” will be made clear in Section 5 with the help of our model for the energy dependence of the phase space volume of a cluster.

As mentioned in the Introduction, a further indication of the inconsistency resulting from ignoring the mixed solid-liquid states and, thus, incorrectly assuming thermodynamic equilibrium is the difference in results obtained in the microcanonical and canonical ensembles. The ensemble defines the different environment, but it should not affect the sought after thermodynamic properties of the system under consideration. There is only one thermodynamic equilibrium state, and this state must be determined identically and independently of the ensemble used. Ignoring this fact has led researchers to consider the inconsistencies in the analysis as exotic thermodynamic attributes [18,19].

5. Model for the Phase Space Volume of a Nanocluster

We seek an analytical model that can accurately describe the true thermodynamics of nanoclusters. Preferably, such a model should allow for the introduction of energy barriers between different microstates of the system in such a way that we may also use the model to describe the spectrum of the dynamical behavior that would be observed for a trapped nanocluster in the microcanonical ensemble. Furthermore, we would like our model to be valid over a useful range of energies, including the phase transition from solid to liquid.

We begin by considering the possible microstates available to a nanocluster assuming only two phases, the solid and liquid. We seek the energy dependence of the phase space volume Γ(E) for an ensemble of clusters in thermodynamic equilibrium. In practice, this could be obtained from the energy probability density ρ(E,T₀) of a canonical ensemble of clusters in true thermodynamic equilibrium at temperature T₀;

$$\mathrm{\Gamma }(E)=\mathrm{\rho }(E,T_0)Z \text{exp}(-E / k_B{T}_0)$$

(3)

with Z the partition function. At any temperature T₀, for each member of the ensemble, there may be one, two, three, etc., up to N (N = number of atoms in the cluster) atoms in the liquid. Each of these possibilities contributes to ρ(E,T₀) and thus to Γ(E). Every one of these possibilities is a microstate that must be counted, weighted (in the canonical ensemble, the microstates have different probabilities [14]) and averaged over in the determination of the thermodynamics.

An alternative, but equivalent and more straightforward procedure is to assume no energy barriers and to develop the phase space volume in the microcanonical ensemble. We have presented this approach in detail in another publication [4], so here, we only give a summary of the procedure. We construct a model for the phase space volume of a nanocluster, including the change at the solid to liquid transition, by considering the contribution to the total phase space of each partial volume Γi constituted by i indistinguishable particles in the liquid phase in interaction with N − i indistinguishable particles in the solid phase:

$${\mathrm{\Gamma }}_i(E)=\left(N!/(N-i)!i!\right){\mathrm{\Gamma }}_i^l(E){\mathrm{\Gamma }}_{N-i}^s(E)$$

(4)

where ${\mathrm{\Gamma }}_i^l(E)$ and ${\mathrm{\Gamma }}_{N-i}^s(E)$ are the liquid and solid phase space volumes. The combinatory factor gives the number of ways to distribute i particles from N identical particles between the liquid and solid phases. The total phase space volume is then obtained by summing over all possible partial volumes constituting all distributions of particles among the solid and liquid: $\mathrm{\Gamma }(E)={\sum }_{i=0}^N{\mathrm{\Gamma }}_i(E)$. Note that the microcanonical ensemble imposes no restrictions on how the energy E is distributed over the system.

The phase space volume for a classical system increases as a power law in the energy, where the power exponent is equal to one half the number of quadratic terms that enter the Hamiltonian for the system. Thus, a simple model of the energy dependence of the phase space volume, which includes the change in the number of degrees of freedom upon melting, for a cluster of N atoms (with total momentum and total angular momentum fixed at zero) is,

$$\mathrm{\Gamma }(E)=c{\displaystyle \sum _{i=0}^N}\frac{N!}{(N-i)!i!}{\left(\frac{E}{E^{*}}\right)}^{6(N-i)/2-6}\cdot {\left(\frac{E}{E^{*}}\right)}^{(6+\mathrm{\lambda })i/2}$$

(5)

where c is a constant and E* is the characteristic energy of the solid to liquid transition. In the harmonic approximation, E* can be taken as the geometric mean of the normal mode vibrational frequencies v_i of the solid, $E^{*}\approx \hslash \cdot \sqrt[3N-6]{{\prod }_{i=1}^{3N-6}{\nu }_i}$. The first energy factor in Equation (5) corresponds to contributions to the phase space volume due to the solid part of the cluster, while the second corresponds to contributions due to the liquid part, with the extra λ modes for storing energy per atom. As mentioned above, for a cluster, there are nominally λ = 2 new modes related to the translational energy of the atoms moving over a two-dimensional surface. The different values of i correspond to the different grades of melting; for i = 0, the cluster is all solid; for i = N, the cluster is all liquid; for i = N/2, half of the atoms are in the solid part and half are in the liquid part of the cluster.

Since the thermodynamics is independent of an arbitrary constant multiplying the phase space volume (only changes in entropy are important), Equation (5) may be rewritten in the more condensed form,

$$\mathrm{\Gamma }(E)=d{\displaystyle \sum _{i=0}^N}\frac{1}{(N-i)!i!}{\left(\frac{E}{E^{*}}\right)}^{3N+i-6}$$

(6)

Given this density of states, it is then straightforward to calculate the thermodynamics of the system using the Boltzmann equation, S(E) = k_B ln Γ(E). The temperature is then given by,

$$T(E)={\left(\frac{\partial S(E)}{\partial E}\right)}_{V,N}^{-1}$$

and the specific heat (heat capacity per atom) by,

$$C_{V,N}(E)=\frac{1}{N}{\left[1-\frac{\mathrm{\Gamma }(E){\mathrm{\Gamma }}^{″}(E)}{{\mathrm{\Gamma }}^{\prime }{(E)}^2}\right]}^{-1}$$

The caloric curve and the specific heat for the cluster Na₁₄₇ obtained using the density of states as determined by Equation (6) are given by the solid line in Figure 4a,b, respectively. These curves represent the results that would be obtained for a cluster in thermodynamic equilibrium. In this case, all mixed microstates (different terms in Equation (6) corresponding to a different number of atoms in the liquid) are included. The specific heat shows a smooth increase from its value of (3N − 6)/N in units of k_B to its value of (4N − 6)/N. The transition is not the abrupt first order transition of the bulk, but of order N.

We may now ask what would happen if our measurements were performed in the microcanonical ensemble where they are affected by the energy barriers. This would correspond to the dynamics of a trapped system. If we assume the extreme case in which all mixed solid-liquid states have high barriers reaching into the transition region, then our system would go directly from the all-solid into the all-liquid state. To model the energy dependence of this phase space volume, it is necessary to remove all intermediate terms in Equation (6) corresponding to the mixed solid-liquid states. This leaves us with just two terms, that of the all-liquid and that of the all-solid state,

$$\mathrm{\Gamma }(E)=d\left[{\left(\frac{E}{E^{*}}\right)}^{3N-6}+{\left(\frac{E}{E^{*}}\right)}^{4N-6}\right]$$

(7)

The corresponding “caloric curve” and “specific heat” curves are given by the dashed lines in Figure 4a,b, respectively. In this case, the transition is not smooth, but abrupt, and the measured specific heat becomes negative. This, as mentioned above, is not a thermodynamic result, since the measured phase space volume given by Equation (7) does not correspond to a system in equilibrium, but instead to a trapped system.

Figure 4. (a) Caloric curves for Na₁₄₇ obtained with the full phase space volume, Equation (6) (solid line), and sampled non-ergodically for the extreme case of all the atoms going to the liquid simultaneously in energy, Equation (7) (dashed line); (b) the corresponding specific heats. Apparent negative specific heat is found for the non-ergodic case. Taken from [4].

Figure 4. (a) Caloric curves for Na₁₄₇ obtained with the full phase space volume, Equation (6) (solid line), and sampled non-ergodically for the extreme case of all the atoms going to the liquid simultaneously in energy, Equation (7) (dashed line); (b) the corresponding specific heats. Apparent negative specific heat is found for the non-ergodic case. Taken from [4].

In reality, different mixed solid-liquid states could have energy barriers of different heights. In fact, surface melting has been readily observed in simulations of core-shell nanoalloys [20,21,22,23]. A more correct description of the energy dependence of the measured phase space volume for such a trapped system is therefore not the extreme case as given by Equation (7), but one in which we have a different E* for each mixed solid-liquid state. Our Equation (6) then becomes:

$$\mathrm{\Gamma }(E)=d{\displaystyle \sum _{i=0}^N}\frac{1}{(N-i)!i!}{\left(\frac{E}{E_i^{*}}\right)}^{3N+i-6}$$

(8)

What E*’s to use depend on the energetics of liquid over solid structures. Obtaining the $E_i^{*}$ from the potential model or experiment directly is not as difficult a task as it would seem at first sight. Given the experimental or simulation specific heat curves, we can fit the specific heat curve obtained by theory, using Equation (8) in Equation (2), by varying the $E_i^{*}$. Figure 5 shows the result of fitting the theoretical specific heat to the specific heat determined through molecular dynamic results at constant energy [24] minimizing the χ² of the fit by varying the $E_i^{*}$’s. The corresponding best fit barrier heights $E_i^{*}$ for the different mixed solid-liquid states with i atoms in the liquid are given in Figure 6.

Figure 5. (a) Caloric curve for Na₂₀ obtained from molecular dynamics runs at constant energy [24] (crosses) and using the model phase space volume Equation (6) (dashed curve). The solid curve is a fit using Equation (8) with the $E_i^{*}$ as given in Figure 6. (b) Corresponding specific heat curves.

Figure 5. (a) Caloric curve for Na₂₀ obtained from molecular dynamics runs at constant energy [24] (crosses) and using the model phase space volume Equation (6) (dashed curve). The solid curve is a fit using Equation (8) with the $E_i^{*}$ as given in Figure 6. (b) Corresponding specific heat curves.

Note that as suggested above, the all-solid to all-liquid barrier ($E_i^{*}$, i = 20) is lower than the $E_i^{*}$ for many mixed solid-liquid states. It is this fact that leads to the false determination of negative heat capacity for larger-sized clusters (e.g., Na₁₄₇).

Figure 6. The energy barriers $E_i^{*}$ for the mixed solid-liquid states with i atoms in the liquid for Na₂₀. Obtained by fitting the model specific heat capacity, using the phase space volume of Equation (8), to molecular dynamics results at constant energy (see Figure 5).

Figure 6. The energy barriers $E_i^{*}$ for the mixed solid-liquid states with i atoms in the liquid for Na₂₀. Obtained by fitting the model specific heat capacity, using the phase space volume of Equation (8), to molecular dynamics results at constant energy (see Figure 5).

6. Discussion and Conclusions

We have studied the dynamics and thermodynamics of nanoclusters in two different environments, the canonical and the microcanonical ensembles. We have shown that equilibrium thermodynamic properties can only be obtained from the canonical ensemble and that nanoclusters in the microcanonical ensemble are trapped systems. Negative heat capacities and differences between results obtained in the canonical and microcanonical ensembles are simply inconsistencies that result from applying the equilibrium thermodynamic formalism to a cluster trapped out of equilibrium.

Nanoclusters differ in their statistical properties from the bulk in that many possible symmetries contribute to the accessible microstates and because energy barriers between solid and mixed solid-liquid states are variable in energy and often below the solid to liquid transition. This is due to the fact that surface atoms are important in the thermodynamics of nanoclusters, and these are proportionately greater in number and less tightly bound than in the bulk.

We have given a simple analytical model to describe the dynamics and thermodynamics of nanoclusters and have shown how this model can be used to understand the inconsistencies in the analysis, such as the determination of negative heat capacity and the differences obtained in the two different ensembles (canonical and microcanonical). We have also used our model to determine the barrier heights for the mixed solid-liquid states, a model that we suggest will be of great utility to the study of the dynamics of nanoclusters.

Finally, within the confines of the heated debate regarding the validity or not of negative heat capacity in nanoclusters, we are often confronted with toy statistical models, which apparently do not suffer from broken ergodicity in the microcanonical ensemble and, yet, demonstrate negative heat capacity (see, for example, [10,11,25,26]). However, in all such cases that have been presented to us so far, we have shown that these models do not represent physically-realistic systems that can reach thermodynamic equilibrium. The thermodynamic formalism can thus not be legitimately applied to these models.

The reason for the illegitimacy of applying the thermodynamic formalism to these toy statistical models has been given in [15]. There, we have shown that under the two basic axioms that must be satisfied in order to derive equilibrium thermodynamics from statistical mechanics, (i) the independence of the microstates and (ii) the a priori equal probability of the microstates, the density of states of a system cannot have any arbitrary dependence on the extensive variables of the system. In particular, we showed that in order to comply with these two basic axioms, the system must have a density of states Γ(X) dependence on the extensive variable X, which obeys the following relation;

$$\left[\frac{\mathrm{\Gamma }(X){\mathrm{\Gamma }}^{″}(X)}{{\mathrm{\Gamma }}^{\prime }{(X)}^2}\right]<1$$

(9)

for any extensive variable and where the prime refers to the differentiation of the density of states with respect to the extensive variable. This can be seen to be just Relation (2) for assuring a positive heat capacity for the case of the extensive variable X being the energy E.

If Relation (9) is violated for any extensive variable X by a particular model, then the model violates one or more of the two basic axioms and, as such, is not treatable under the thermodynamic formalism. A careful analysis of Relation (9) shows that valid thermodynamic models must have a number of microstates that grows not faster than a power law or, more exactly, not faster than a non-infinite sum of power laws, with any extensive variable [15]. If one anyhow insists on applying thermodynamic formalism on these models that do not satisfy Relation (9), then inconsistencies in the analysis will result, one of them being the determination of “negative heat capacity”.

Since any system trapped out of equilibrium will demonstrate macroscopic results that depend on the initial conditions, we suggest that all previous “thermodynamic” results on nanoclusters should be carefully re-examined.