1. Introduction
Non-equilibrium thermodynamics provides a general description of irreversible processes taking place in large-scale systems that integrate a great number of degrees of freedom [
1]. The theory applies when the system is in local equilibrium, in which case the usual thermodynamic quantities retain their meaning and the thermodynamic relationships are formally identical to the ones formulated at equilibrium. Non-equilibrium thermodynamics accounts for the linear response domain in which the response of the system is linear in the perturbation exerted to remove it from equilibrium [
2,
3]. Moreover, the description is performed in terms of average values not accounting for the presence of fluctuations. Whereas the linear approximation holds for transport processes such as heat conduction and mass diffusion, even in the presence of large or very large gradients [
4,
5,
6], it is not appropriate to describe activated processes in which the system is intrinsically nonlinear. Small systems [
7], such as an RNA molecule subjected to an external force [
8], in which fluctuations and nonlinearities can be very important, are beyond the scope of this theory.
In equilibrium, the probability distribution is related to a thermodynamic potential which represents the minimum work needed to establish the state of the system [
9]. Far from equilibrium, however, the probability must be determined from master equations or kinetic equations of the Fokker–Planck type [
10,
11]. The latter has the form of a diffusion equation for the probability distribution, valid when the stochastic process is Gaussian. For this type of noise, the stochastic variable varies in a small amount for short time intervals, as in a diffusion process.
The connection between mesoscopic dynamics and thermodynamics [
12,
13,
14,
15] can be established through the derivation of the Fokker–Planck equation from a diffusion process of the probability compatible with the statistical formulation of the second law [
16,
17]. This new approach, mesoscopic non-equilibrium thermodynamics, offers a method to analyze the mesoscopic dynamics of thermodynamic systems, incorporating the presence of fluctuations and overcoming the restriction of linearity inherent to non-equilibrium thermodynamics [
18].
In this article, we will show that the probabilistic interpretation of the density together with conservation laws in phase space and positiveness of global entropy changes sets the basis of a theory that follows the operational scheme of non-equilibrium thermodynamics but of a much broader range of applicability. The fact that it is based on probabilities instead of densities allows us to consider mesoscopic systems and their fluctuations. The situations that can be studied with this formalism include, among others, slow relaxation processes, barrier crossing dynamics, chemical reactions and entropic transport. These processes are in general non-linear and influenced by the presence of fluctuations.
The article is structured as follows. In
Section 2, we present the general framework of mesoscopic non-equilibrium thermodynamics. In
Section 3, we analyze the case of a single molecule subjected to a force whereas in
Section 4, we discuss the case of activation in small-scale systems.
Section 5 is devoted to present our main conclusions.
2. Mesoscopic Dynamics of Small-Scale Systems
The characterization of small-scale systems is performed by identifying the degrees of freedom that have not yet relaxed at the observational scale and that therefore exert an influence in the overall dynamics of the system. These degrees of freedom, denoted by means of the set of coordinates (), could be, for example, the velocity and orientation of a particle, the size of a macromolecule, the number of building blocks of a meso-structures or any coordinate or order parameter whose values define the state of the small system in a phase space.
A mesoscopic description of the system that takes into account the presence of fluctuations must be performed through the knowledge of the probability density
. The statistical expression of the entropy of the system
in terms of this probability can be expressed by the Gibbs entropy postulate [
1,
12,
13]
where
denotes the entropy when the degrees of freedom
are in equilibrium. The equilibrium probability density
can be related to the minimum reversible work required to create that state [
9] through the expression
here
is Boltzmann’s constant, and
is the temperature of the heat bath. The minimum work can in general be expressed as
, where
is an intensive parameter and
its conjugated extensive variable. This general form stands for mechanical, electrical, magnetic, surface work,
etc., performed on the system [
19].
The dynamics of the mesoscopic degrees of freedom can be analyzed from the statistical mechanics definition of the entropy. Taking variations in Equation (1), one obtains
To derive the expression of the current, we take the time derivative of the entropy in Equation (3) and use the continuity equation
with
a current in the space of mesoscopic coordinates. After a partial integration, one then arrives at the expression of the mesoscopic entropy production [
12]
This quantity expresses in the form of current-force pairs, the latter being the gradients in the space of mesoscopic variables. We will now assume a linear dependence between current and force and establish the linear relationship
where
is an Onsager coefficient [
1,
20] which, in general, depends on the probability
interpreted as a state variable in the thermodynamic sense and on the mesoscopic coordinates
.
The kinetic equation follows by substituting the probability current given in Equation (6) into the continuity Equation (4). One obtains the Fokker–Planck equation for the evolution of the probability density in
-space
where the diffusion coefficient is defined as
where we have assumed that the Onsager coefficient is a linear function of the probability density.
Under constant temperature and pressure conditions for which the minimum work is given by the Gibbs free energy
,
, where
is the enthalpy, this equation transforms into the Fokker–Planck equation for a system in the presence of a free energy barrier:
Mesoscopic non-equilibrium thermodynamics provides a general formalism able to analyze the dynamics of small-scale systems away from equilibrium from the knowledge of the equilibrium thermodynamic potential of the system.
3. Single Molecule Stretching
The stretching of a DNA molecule by means of an optical tweezer has been proposed as a prototypical example of a system far from equilibrium [
21]. The analysis of the experiments reveals two features: the macromolecule is in mechanical equilibrium and fluctuations may play an important role.
Typical forces exerted on the particles are of the order of 10 pN, [
22]. When the size of the macromolecule is of the order of
, the host liquid density is
, and the viscosity is
, one has
and,
where
is the mass of the molecule and
the friction coefficient. Therefore, variations in time of the force are very small and consequently inertial effects can be neglected [
23]. The macromolecule is practically in mechanical equilibrium.
The work done by the applied force is
, with
the elongation of the macromolecule. For typical values of the force
, and
[
22], the work is
which shows that thermal fluctuations whose associated energy is of the order of
play a role in the kinetics. As a consequence, one must adopt a probabilistic description in terms of the probability
. The molecule is immersed in a liquid at rest which acts as a thermal bath. This implies that the noise is Gaussian and consequently that the evolution of the probability density is governed by a diffusion equation for the probability density, the Smoluchowski equation.
To obtain this equation, we will use the framework of mesoscopic non-equilibrium thermodynamics, [
12,
13]. The starting point is the Gibbs entropy
which is now written in terms of the elongation of the molecule;
and
are the entropy and the probability distribution of a reference state. Taking variations of this equation, one obtains,
Here is the local entropy and the corresponding chemical potential, where the total potential, , consists of the energy barrier of the molecule and the work done by the external force. The force exerted by an optical trap is given by , where is a constant and the time-dependent position of the center of the trap.
Comparing the integrands of the second and fourth terms of Equation (13), one obtains the local thermodynamic relation,
From this equation, one can easily derive the entropy production rate of the stretching of the molecule,
From which one derives the expression for the current,
Proceeding as we did in
Section 2, one obtains the Smoluchowski equation,
From this equation, we can analyze the role played by the fluctuations in the stretching process. The solution is
where
. The relation between forward and backward probabilities is given by [
24]
In the small fluctuations regime, when the energy of the particle is much larger than the thermal energy: , one has from Equation (19) . The probability for the particle to move in the direction opposed to the force is then very small. In the opposite limit of large fluctuations, the work on the DNA molecule is not very different from thermal energy. The probabilities for backward and forward motions are in this case of the same order of magnitude.
When fluctuations are important, the work is a fluctuating quantity. In the case in which the intrinsic potential is harmonic:
, with
an elastic constant, one can obtain the average [
19]
where the equilibrium position of the bead is given by,
In the case in which
, the equilibrium position of the particle practically coincides with the position of the trap
. The previous average reduces in this case, the limit of small fluctuations, to
This expression shows that free Gibbs energy differences follow from measurements of the work. In the case of large fluctuations, Equation (22) which corresponds to the so-called Jarzynski equality is no longer valid and one has to use the general expression (20) in which the argument of the exponential is not the free energy. This lack of correspondence between work and free energy through a relation different from Equation (22) has also been observed in the Brownian motion of a particle in a stationary flow [
25]. A discussion about the failure of the work-Hamiltonian connection necessary for the validity of that equality has been presented in [
19].
Stretching of a single RNA molecule has also been analyzed under the perspective of mesoscopic non-equilibrium thermodynamics [
8]. Moreover, this theory has been applied to analyze the kinetics of molecular motors [
26], and pumps [
27]. When and how mesoscopic non-equilibrium thermodynamics can be used to describe small-scale biological systems is discussed in [
15].
4. Activated Process in Small-Scale Systems
Processes such as cluster formation, protein ligand binding, dissipative self-assembly, adsorption of a single molecule on a substrate and chemical reactions, need of a minimum of energy to proceed. They can be modeled by a particle crossing a free energy barrier that separates two well-differentiated states located at the minima at each side of the barrier [
28,
29] and are generically referred to as activated processes [
30]. Their intrinsic nonlinear nature means that they cannot be treated by non-equilibrium thermodynamics. This is the case of biochemical cycle kinetics treated in [
31].
Non-equilibrium thermodynamics offers a partial description of the process, performed in terms of the initial and final positions, ignoring the transient states. This fact results in a linear behaviour of the current in terms of the affinity which only agrees with the law of mass action for small values of the affinity [
1]. If we consider the process at shorter time scales, the state of the system instead of jumping suddenly from the initial to the final state progressively transforms by passing through successive molecular configurations. These configurations can be parametrized by a reaction coordinate
. At these time scales, one may assume that the reaction coordinate undergoes a diffusion process through a potential barrier separating the initial from the final states.
At observational time scales, the system is mostly found at the minima of the potential
and
. In the quasi-stationary limit, when the energy barrier is much higher than the thermal energy and intra-well relaxation has already taken place, the probability distribution is strongly peaked at these values and almost zero everywhere else. Under these conditions, the Fokker–Planck description, leads to a kinetic equation in which the net reaction rate satisfies the mass action law [
13].
The current obtained from the mesoscopic entropy production (6) can be rewritten in terms of the local fugacity defined along the reaction coordinate
as
which can be expressed as
where
is the diffusion coefficient. We now assume that
is constant and integrate from 1 to 2 to obtain the nonlinear kinetic law for the averaged current [
32]
where the states 1 and 2 are characterized by the values of the reaction coordinate
and
, respectively. This equation that can also be expressed as
where
and
is the affinity, is the law of mass action usually found in different activated processes [
27,
33,
34].
The scheme presented reproduces the results of the rate theory [
28]. Equation (26) can be written in terms of the forward and backward reaction rates,
and
, as
where
and
are the populations at both states. The reaction rates are given in terms of the values of the reaction potential
at states 1 and 2,
and
Fluctuations in the population densities at both wells can be analyzed by means of fluctuating hydrodynamics [
32]. A coarse-graining of the description in terms of the initial and final states only may lead to violation of the fluctuation-dissipation theorem [
35]. In equilibrium, the current vanishes, therefore one has the detailed balance condition
, or equivalently
which shows that the forward and backward reaction constants cannot be chosen independently.
We can now analyze the case in which the process
is coupled to
in the sense that the forward and backward reaction rates of both processes are equal. In the second process, the concentration of the components
and
can be controlled externally (see
Figure 1). The current is in this case given by
where the initial and final fugacities are
When both reactions are in equilibrium, the detailed balance condition imposes
Changes in the concentrations of C and D drive the system away from equilibrium to a state in which detailed balance is not fulfilled, as happens in open cyclic enzyme reactions with substrates [
36].
Figure 1.
The process satisfies detailed balance; consequently, the reaction rates obey Equation (30). When this process is coupled to , which is not in equilibrium, detailed balance condition (33) is no longer applicable.
Figure 1.
The process satisfies detailed balance; consequently, the reaction rates obey Equation (30). When this process is coupled to , which is not in equilibrium, detailed balance condition (33) is no longer applicable.
This feature can also be observed in open triangular reactions usually found in biochemical cycles [
18]. The mesoscopic non-equilibrium thermodynamics approach to the kinetics of far from equilibrium activated processes has been applied to nucleation kinetics [
37], to analyze the role played by the translational and rotational degrees of freedom of the clusters [
38] and the influence of external gradients [
39,
40].
Our model can also be used in the case of enzymatic reactions such as the Michaelis–Menten reaction [
41], in which a substrate S transforms into a product P due to the intervention of an enzyme E that acts as a catalyst, remaining unaltered during the process:
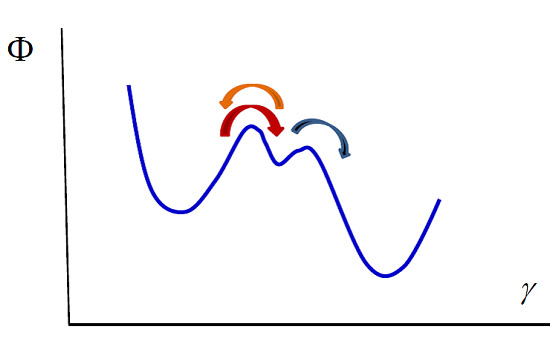
The transformations can be viewed as diffusion in a potential along a reaction coordinate. The potential exhibits two barriers that correspond to the two reactions (see
Figure 2). Integrating the diffusion equation for values of the reaction coordinate corresponding to the two reactions in the way we indicated previously, one obtains the kinetic equations. The first reaction is in a stationary state, with
or equivalently
The second reaction takes place only in the forward direction, therefore
Using the enzyme mass conservation,
, and Equation (35), one obtains
Substituting this result in the second kinetic equation one obtains the concentration of product rate
which shows that at small values of
, the rate is linear whereas at large values it saturates to
.
Figure 2.
Michaelis–Menten enzymatic reaction. The whole process can be viewed as diffusion in the potential indicated in the figure. The left and right wells correspond to the substrate and the product. The central well denotes the intermediate state, the formation of the complex enzyme-substrate (ES). The arrows indicate the direction of the processes.
Figure 2.
Michaelis–Menten enzymatic reaction. The whole process can be viewed as diffusion in the potential indicated in the figure. The left and right wells correspond to the substrate and the product. The central well denotes the intermediate state, the formation of the complex enzyme-substrate (ES). The arrows indicate the direction of the processes.