On Hölder Projective Divergences
Abstract
:1. Introduction: Inequality, Proper Divergence and Improper Pseudo-Divergence
1.1. Statistical Divergences from Inequality Gaps
1.2. Pseudo-Divergences and the Axiom of Indiscernibility
- Non-negativeness: for any ;
- Reachable indiscernibility:
- , there exists , such that ,
- , there exists , such that .
- Positive correlation: if , then for any , .
1.3. Prior Work and Contributions
- Define the tri-parametric family of Hölder improper pseudo-divergences (HPDs) in Section 2 and the bi-parametric family of Hölder proper divergences in Section 3 (HDs) for positive and probability measures, and study their properties (including their relationships with skewed Bhattacharyya distances [8] via escort distributions);
- Report closed-form expressions of those divergences for exponential families when the natural parameter space is a cone or affine (including, but not limited to the cases of categorical distributions and multivariate Gaussian distributions) in Section 4;
- Provide approximation techniques to compute those divergences between mixtures based on log-sum-exp inequalities in Section 4.6;
- Describe a variational center-based clustering technique based on the convex-concave procedure for computing Hölder centroids, and report our experimental results in Section 5.
1.4. Organization
2. Hölder Pseudo-Divergence: Definition and Properties
2.1. Definition
2.2. Properness and Improperness
2.3. Reference Duality
2.4. HPD is a Projective Divergence
2.5. Escort Distributions and Skew Bhattacharyya Divergences
3. Proper Hölder Divergence
3.1. Definition
3.2. Special Case: The Cauchy–Schwarz Divergence
3.3. Limit Cases of Hölder Divergences and Statistical Estimation
4. Closed-Form Expressions of HPD and HD for Conic and Affine Exponential Families
4.1. Case Study: Categorical Distributions
4.2. Case Study: Bernoulli Distribution
4.3. Case Study: MultiVariate Normal Distributions
4.4. Case Study: Zero-Centered Laplace Distribution
4.5. Case Study: Wishart Distribution
4.6. Approximating Hölder Projective Divergences for Statistical Mixtures
5. Hölder Centroids and Center-Based Clustering
5.1. Hölder Centroids
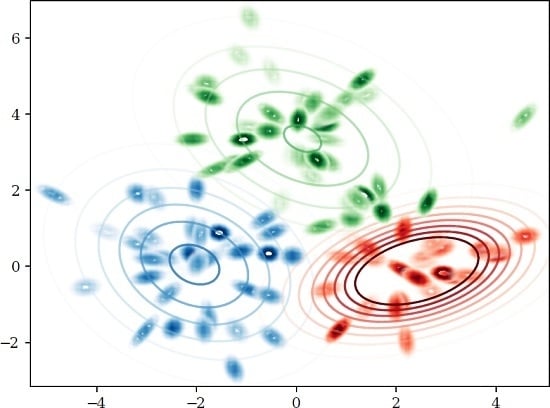
5.2. Clustering Based on Symmetric Hölder Divergences
| Algorithm 1: Hölder variational k-means. |
 |
6. Conclusions and Perspectives
- To reveal that Hölder pseudo-divergences on escort distributions amount to skew Bhattacharyya divergences [8],
- To transform the improper Hölder pseudo-divergences into proper Hölder divergences, and vice versa.
- In an estimation scenario, we can usually pre-compute according to . Then, the estimation will automatically target at . We call this technique “pre-aim.”For example, given positive measure , we first find to satisfy . We have that satisfies this condition. Then, a proper divergence between and can be obtained by aiming towards . For conjugate exponents α and β,This means that the pre-aim technique of HPD is equivalent to HD when we set .As an alternative implementation of pre-aim, since , a proper divergence between and can be constructed by measuring:turning out again to belong to the class of HD.In practice, HD as a bi-parametric family may be less used than HPD with pre-aim because of the difficulty in choosing the parameter γ and because that HD has a slightly more complicated expression. The family of HD connecting CS divergence with skew Bhattacharyya divergence [8] is nevertheless of theoretical importance.
- In manifold learning [44,45,46,47], it is an essential topic to align two category distributions and corresponding respectively to the input and output [47], both for learning and for performance evaluation. In this case, the dimensionality of the statistical manifold that encompasses and is so high that to preserve monotonically in the resulting is already a difficult non-linear optimization and could be sufficient for the application, while preserving perfectly the input is not so meaningful because of the input noise. It is then much easier to define pseudo-divergences using inequalities which do not necessarily need to be proper with potentially more choices. On the other hand, projective divergences including Hölder divergences introduced in this work are more meaningful in manifold learning than KL divergence (which is widely used) because they give scale invariance of the probability densities, meaning that one can define positive similarities then directly align these similarities, which is guaranteed to be equivalent to aligning the corresponding distributions. This could potentially give unified perspectives in between the two approaches of similarity-based manifold learning [46] and the probabilistic approach [44].
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Hölder proper non-projective Scored-induced divergence [18] | |
| Hölder improper projective pseudo-divergence (new) | |
| Hölder proper projective divergence (new) | |
| Hölder proper projective escort divergence (new) | |
| Kullback-Leibler divergence [10] | |
| Cauchy–Schwarz divergence [2] | |
| B | Bhattacharyya distance [25] |
| skew Bhattacharyya distance [8] | |
| γ-divergence (score-induced) [11] | |
| escort distributions | |
| Hölder conjugate pair of exponents: | |
| Hölder conjugate exponent: | |
| natural parameters of exponential family distributions | |
| support of distributions | |
| μ | Lebesgue measure |
| Lebesgue space of functions f such that |
Appendix A. Proof of Hölder Ordinary and Reverse Inequalities
References
- Mitrinovic, D.S.; Pecaric, J.; Fink, A.M. Classical and New Inequalities in Analysis; Springer Science & Business Media: New York, NY, USA, 2013; Volume 61. [Google Scholar]
- Budka, M.; Gabrys, B.; Musial, K. On accuracy of PDF divergence estimators and their applicability to representative data sampling. Entropy 2011, 13, 1229–1266. [Google Scholar] [CrossRef]
- Amari, S.I. Information Geometry and Its Applications; Applied Mathematical Sciences series; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Rao, C.R. Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Nielsen, F.; Nock, R. Total Jensen divergences: Definition, properties and clustering. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 2016–2020.
- Burbea, J.; Rao, C. On the convexity of some divergence measures based on entropy functions. IEEE Trans. Inf. Theory 1982, 28, 489–495. [Google Scholar] [CrossRef]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Fujisawa, H.; Eguchi, S. Robust parameter estimation with a small bias against heavy contamination. J. Multivar. Anal. 2008, 99, 2053–2081. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Patch Matching with Polynomial Exponential Families and Projective Divergences. In Proceedings of the 9th International Conference on Similarity Search and Applications, Tokyo, Japan, 24–26 October 2016; pp. 109–116.
- Zhang, J. Divergence function, duality, and convex analysis. Neural Comput. 2004, 16, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Nonparametric information geometry: From divergence function to referential-representational biduality on statistical manifolds. Entropy 2013, 15, 5384–5418. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. A closed-form expression for the Sharma–Mittal entropy of exponential families. J. Phys. A Math. Theor. 2011, 45, 032003. [Google Scholar] [CrossRef]
- De Souza, D.C.; Vigelis, R.F.; Cavalcante, C.C. Geometry Induced by a Generalization of Rényi Divergence. Entropy 2016, 18, 407. [Google Scholar] [CrossRef]
- Kanamori, T.; Fujisawa, H. Affine invariant divergences associated with proper composite scoring rules and their applications. Bernoulli 2014, 20, 2278–2304. [Google Scholar] [CrossRef]
- Kanamori, T. Scale-invariant divergences for density functions. Entropy 2014, 16, 2611–2628. [Google Scholar] [CrossRef]
- Nielsen, F.; Garcia, V. Statistical exponential families: A digest with flash cards. arXiv, 2009; arXiv:0911.4863. [Google Scholar]
- Rogers, L.J. An extension of a certain theorem in inequalities. Messenger Math. 1888, 17, 145–150. [Google Scholar]
- Holder, O.L. Über einen Mittelwertssatz. Nachr. Akad. Wiss. Gottingen Math. Phys. Kl. 1889, 44, 38–47. [Google Scholar]
- Hasanbelliu, E.; Giraldo, L.S.; Principe, J.C. Information theoretic shape matching. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2436–2451. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, F. Closed-form information-theoretic divergences for statistical mixtures. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 11–15 November 2012; pp. 1723–1726.
- Zhang, J. Reference duality and representation duality in information geometry. Am. Inst. Phys. Conf. Ser. 2015, 1641, 130–146. [Google Scholar]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- Srivastava, A.; Jermyn, I.; Joshi, S. Riemannian analysis of probability density functions with applications in vision. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8.
- Nielsen, F.; Nock, R. On the Chi Square and Higher-Order Chi Distances for Approximating f-Divergences. IEEE Signal Process. Lett. 2014, 1, 10–13. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R. Skew Jensen-Bregman Voronoi diagrams. In Transactions on Computational Science XIV; Springer: New York, NY, USA, 2011; pp. 102–128. [Google Scholar]
- Nielsen, F.; Sun, K. Guaranteed Bounds on Information-Theoretic Measures of Univariate Mixtures Using Piecewise Log-Sum-Exp Inequalities. Entropy 2016, 18, 442. [Google Scholar] [CrossRef]
- Notsu, A.; Komori, O.; Eguchi, S. Spontaneous clustering via minimum gamma-divergence. Neural Comput. 2014, 26, 421–448. [Google Scholar] [CrossRef] [PubMed]
- Rigazio, L.; Tsakam, B.; Junqua, J.C. An optimal Bhattacharyya centroid algorithm for Gaussian clustering with applications in automatic speech recognition. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Volume 3, pp. 1599–1602.
- Davis, J.V.; Dhillon, I.S. Differential Entropic Clustering of Multivariate Gaussians. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2006; pp. 337–344.
- Nielsen, F.; Nock, R. Clustering multivariate normal distributions. In Emerging Trends in Visual Computing; Springer: New York, NY, USA, 2009; pp. 164–174. [Google Scholar]
- Allamigeon, X.; Gaubert, S.; Goubault, E.; Putot, S.; Stott, N. A scalable algebraic method to infer quadratic invariants of switched systems. In Proceedings of the 12th International Conference on Embedded Software, Amsterdam, The Netherlands, 4–9 October 2015; pp. 75–84.
- Sun, D.L.; Févotte, C. Alternating direction method of multipliers for non-negative matrix factorization with the beta-divergence. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6201–6205.
- Banerjee, A.; Dhillon, I.S.; Ghosh, J.; Sra, S. Clustering on the unit hypersphere using von Mises-Fisher distributions. J. Mach. Learn. Res. 2005, 6, 1345–1382. [Google Scholar]
- Gopal, S.; Yang, Y. Von Mises-Fisher Clustering Models. J. Mach. Learn. Res. 2014, 32, 154–162. [Google Scholar]
- Rami, H.; Belmerhnia, L.; Drissi El Maliani, A.; El Hassouni, M. Texture Retrieval Using Mixtures of Generalized Gaussian Distribution and Cauchy-Schwarz Divergence in Wavelet Domain. Image Commun. 2016, 42, 45–58. [Google Scholar] [CrossRef]
- Bunte, K.; Haase, S.; Biehl, M.; Villmann, T. Stochastic neighbor embedding (SNE) for dimension reduction and visualization using arbitrary divergences. Neurocomputing 2012, 90, 23–45. [Google Scholar] [CrossRef]
- Villmann, T.; Haase, S. Divergence-based vector quantization. Neural Comput. 2011, 23, 1343–1392. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.B.; Ahuja, N. Saliency detection via divergence analysis: A unified perspective. In Proceedings of the 2012 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 11–15 November 2012; pp. 2748–2751.
- Pardo, L. Statistical Inference Based on Divergence Measures; CRC Press: Abingdon, UK, 2005. [Google Scholar]
- Basu, A.; Shioya, H.; Park, C. Statistical Inference: The Minimum Distance Approach; CRC Press: Abingdon, UK, 2011. [Google Scholar]
- Hinton, G.E.; Roweis, S.T. Stochastic Neighbor Embedding. In Advances in Neural Information Processing Systems 15 (NIPS); MIT Press: Vancouver, BC, Canada, 2002; pp. 833–840. [Google Scholar]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Carreira-Perpiñán, M.Á. The Elastic Embedding Algorithm for Dimensionality Reduction. In Proceedings of the International Conference on Machine Learning, Haifa, Israel, 21–25 June 2010; pp. 167–174.
- Sun, K.; Marchand-Maillet, S. An Information Geometry of Statistical Manifold Learning. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1–9.
- Cheung, W.S. Generalizations of Hölder’s inequality. Int. J. Math. Math. Sci. 2001, 26, 7–10. [Google Scholar] [CrossRef]
- Hazewinkel, M. Encyclopedia of Mathematics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Chen, G.S.; Shi, X.J. Generalizations of Hölder inequalities for Csiszár’s f -divergence. J. Inequal. Appl. 2013, 2013, 151. [Google Scholar] [CrossRef]
- Nielsen, F.; Sun, K.; Marchand-Maillet, S. On Hölder Projective Divergences. 2017. Available online: https://www.lix.polytechnique.fr/~nielsen/HPD/ (accessed on 16 March 2017).
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]





| k (#Clusters) | n (#Samples) | (CS) | |||
|---|---|---|---|---|---|
| 2 | 50 | ||||
| 100 | |||||
| 3 | 50 | ||||
| 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, F.; Sun, K.; Marchand-Maillet, S. On Hölder Projective Divergences. Entropy 2017, 19, 122. https://doi.org/10.3390/e19030122
Nielsen F, Sun K, Marchand-Maillet S. On Hölder Projective Divergences. Entropy. 2017; 19(3):122. https://doi.org/10.3390/e19030122
Chicago/Turabian StyleNielsen, Frank, Ke Sun, and Stéphane Marchand-Maillet. 2017. "On Hölder Projective Divergences" Entropy 19, no. 3: 122. https://doi.org/10.3390/e19030122
APA StyleNielsen, F., Sun, K., & Marchand-Maillet, S. (2017). On Hölder Projective Divergences. Entropy, 19(3), 122. https://doi.org/10.3390/e19030122