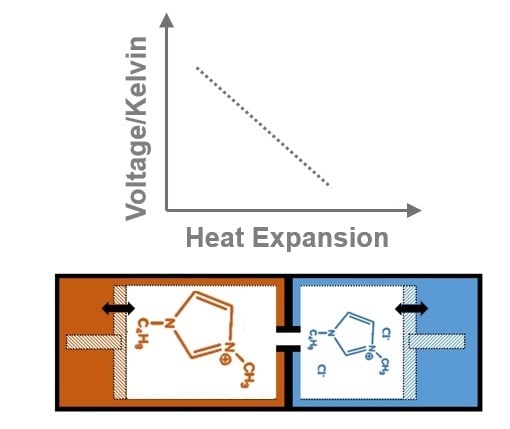
Role of Heat Expansion with a Series of Ionic Liquids: The Case for Isochoric Thermoelectric Generators and Minimal Steric Repulsion
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Analysis
4. Discussion and Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonetti, M.; Nakamae, S.; Huang, B.T.; Salez, T.J.; Wiertel-Gasquet, C.; Roger, M. Thermoelectric energy recovery at ionic-liquid/electrode interface. J. Chem. Phys. 2015, 142. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, S. Thermal diffusion in liquid mixtures and polymer solutions. J. Phys. Condens. Matter 2004, 16, R357–R379. [Google Scholar] [CrossRef]
- Samsonidze, G.; Kozinsky, B. Accelerated Screening of Thermoelectric Materials by First-Principles Computations of Electron-Phonon Scattering. Adv. Energy Mater. 2018, 8, 1800246. [Google Scholar] [CrossRef]
- Laux, E.; Uhl, S.; Jeandupeux, L.; López, P.P.; Sanglard, P.; Vanoli, E.; Marti, R.; Keppner, H. Thermoelectric Generators Based on Ionic Liquids. J. Electron. Mater. 2018, 47, 3193–3197. [Google Scholar] [CrossRef] [Green Version]
- Duan, J.; Feng, G.; Yu, B.; Li, J.; Chen, M.; Yang, P.; Feng, J.; Liu, K.; Zhou, J. Aqueous thermogalvanic cells with a high Seebeck coefficient for low-grade heat harvest. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Salez, T.J.; Huang, B.T.; Rietjens, M.; Bonetti, M.; Wiertel-Gasquet, C.; Roger, M.; Filomeno, C.L.; Dubois, E.; Perzynski, R.; Nakamae, S. Can charged colloidal particles increase the thermoelectric energy conversion efficiency? Phys. Chem. Chem. Phys. 2017, 19, 9409–9416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecæur, P. Internal convection in thermoelectric generator models. J. Phys. Conf. Ser. 2012, 395, 012103. [Google Scholar] [CrossRef]
- Gunawan, A.; Li, H.; Lin, C.H.; Buttry, D.A.; Mujica, V.; Taylor, R.A.; Prasher, R.S.; Phelan, P.E. The amplifying effect of natural convection on power generation of thermogalvanic cells. Int. J. Heat Mass Transf. 2014, 78, 423–434. [Google Scholar] [CrossRef]
- Novev, J.K.; Compton, R.G. Natural convection effects in electrochemical systems. Curr. Opin. Electrochem. 2018, 7, 118–129. [Google Scholar] [CrossRef]
- Salez, T.; Nakamae, S.; Perzynski, R.; Mériguet, G.; Cebers, A.; Roger, M. Thermoelectricity and Thermodiffusion in Magnetic Nanofluids: Entropic Analysis. Entropy 2018, 20, 405. [Google Scholar] [CrossRef]
- Li, X.; Batchelor-McAuley, C.; Novev, J.K.; Compton, R.G. A thermostated cell for electrochemistry: minimising natural convection and investigating the role of evaporation and radiation. Phys. Chem. Chem. Phys. 2018, 20, 11794–11804. [Google Scholar] [CrossRef] [PubMed]
- Laux, E.; Uhl, S.; Gauthier, N.; Jeandupeux, L.; Keppner, H.; López, P.P.; Pauline, S.; Vanoli, E.; Marti, R. Development of Thermoelectric generator based on Ionic Liquids for high temperature applications. Mater. Today Proc. 2018, 5, 10195–10202. [Google Scholar] [CrossRef]
- Vigolo, D.; Buzzaccaro, S.; Piazza, R. Thermophoresis and Thermoelectricity in Surfactant Solutions. Langmuir 2010, 26, 7792–7801. [Google Scholar] [CrossRef] [PubMed]
- Shukla, M.; Srivastava, N.; Saha, S. Interactions and Transitions in Imidazolium Cation Based Ionic Liquids. In Ionic Liquids; Handy, S.T., Ed.; IntechOpen: Rijeka, Croatia, 2011; Chapter 7. [Google Scholar] [CrossRef]
- Petra, C.; Attila, G.; Katalin, B.B.; Laszlo, G. Dielectric Properties of Ionic Liquids Proposed to Be Used in Batteries. In Ionic Liquids - Classes and Properties; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef] [Green Version]
- Keppner, H.; Uhl, S.; Laux, E.; Jeandupeux, L.; Tschanz, J.; Journot, T. Ionic Liquid-based Thermoelectric Generator: Links between Liquid Data and Generator Characteristics. Mater. Today Proc. 2015, 2, 680–689. [Google Scholar] [CrossRef]
- Alcalde, R.; García, G.; Atilhan, M.; Aparicio, S. Systematic Study on the Viscosity of Ionic Liquids: Measurement and Prediction. Ind. Eng. Chem. Res. 2015, 54, 10918–10924. [Google Scholar] [CrossRef]
- Endres, F. Physical chemistry of ionic liquids. Phys. Chem. Chem. Phys. 2010, 12, 1648. [Google Scholar] [CrossRef]
- Abraham, T.J.; MacFarlane, D.R.; Pringle, J.M. Seebeck coefficients in ionic liquids—prospects for thermo-electrochemical cells. Chem. Commun. 2011, 47, 6260. [Google Scholar] [CrossRef]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Lall, S.I.; Mancheno, D.; Castro, S.; Behaj, V.; Cohen, J.I.; Engel, R. Polycations. Part X. LIPs, a new category of room temperature ionic liquid based on polyammonium salts. Chem. Commun. 2000, 2413–2414. [Google Scholar] [CrossRef]
- Patra, R.N.; Gardas, R.L. Effect of Nitro Groups on Desulfurization Efficiency of Benzyl-Substituted Imidiazolium-Based Ionic Liquids: Experimental and Computational Approach. Energy Fuels 2019, 33, 7659–7666. [Google Scholar] [CrossRef]
- Chandran, D.; Khalid, M.; Walvekar, R.; Mubarak, N.M.; Dharaskar, S.; Wong, W.Y.; Gupta, T.C.S.M. Deep eutectic solvents for extraction-desulphurization: A review. J. Mol. Liq. 2019, 275, 312–322. [Google Scholar] [CrossRef]
- Zhang, Z.; Kang, N.; Wang, J.; Sui, H.; He, L.; Li, X. Synthesis and application of amino acid ionic liquid-based deep eutectic solvents for oil-carbonate mineral separation. Chem. Eng. Sci. 2018, 181, 264–271. [Google Scholar] [CrossRef]
- Pérez, P.; Uhl, S.; Laux, E.; Sanglard, P.; Marti, R.; Keppner, H.; Vanoli, E. Synthesis and Structure modification of Ionic Liquids to optimize their Thermoelectric Properties. Mater. Today Proc. 2018, 5, 10298–10305. [Google Scholar] [CrossRef]
- Bonetti, M.; Nakamae, S.; Roger, M.; Guenoun, P. Huge Seebeck coefficients in nonaqueous electrolytes. J. Chem. Phys. 2011, 134, 114513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giglio, M.; Vendramini, A. Thermal-Diffusion Measurements near a Consolute Critical Point. Phys. Rev. Lett. 1975, 34, 561–564. [Google Scholar] [CrossRef]
- Gunawan, A.; Lin, C.H.; Buttry, D.A.; Mujica, V.; Taylor, R.A.; Prasher, R.S.; Phelan, P.E. Liquid Thermoelectrics: Review of Recent And Limited New Data of Thermogalvanic Cell Experiments. Nanosc. Microsc. Therm. Eng. 2013, 17, 304–323. [Google Scholar] [CrossRef]
- Uhl, S.; Laux, E.; Journot, T.; Jeandupeux, L.; Charmet, J.; Keppner, H. Development of Flexible Micro-Thermo-electrochemical Generators Based on Ionic Liquids. J. Electron. Mater. 2014, 43, 3758–3764. [Google Scholar] [CrossRef]
- Perkin, S.; Crowhurst, L.; Niedermeyer, H.; Welton, T.; Smith, A.M.; Gosvami, N.N. Self-assembly in the electrical double layer of ionic liquids. Chem. Commun. 2011, 47, 6572. [Google Scholar] [CrossRef]
- Fedorov, M.; Georgi, N.; Kornyshev, A. Double layer in ionic liquids: The nature of the camel shape of capacitance. Electrochem. Commun. 2010, 12, 296–299. [Google Scholar] [CrossRef]
- Abdel-Aal, S.K.; Kocher-Oberlehner, G.; Ionov, A.; Mozhchil, R.N. Effect of organic chain length on structure, electronic composition, lattice potential energy, and optical properties of 2D hybrid perovskites [(NH3)(CH2) n (NH3)]CuCl4, n = 2–9. Appl. Phys. A 2017, 123. [Google Scholar] [CrossRef]
- Ferreira, A.R.; Freire, M.G.; Ribeiro, J.C.; Lopes, F.M.; Crespo, J.G.; Coutinho, J.A.P. An Overview of the Liquid-Liquid Equilibria of (Ionic Liquid Hydrocarbon) Binary Systems and Their Modeling by the Conductor-like Screening Model for Real Solvents. Ind. Eng. Chem. Res. 2011, 50, 5279–5294. [Google Scholar] [CrossRef]
- Krossing, I.; Slattery, J.M.; Daguenet, C.; Dyson, P.J.; Oleinikova, A.; Weingärtner, H. Why Are Ionic Liquids Liquid? A Simple Explanation Based on Lattice and Solvation Energies. J. Am. Chem. Soc. 2006, 128, 13427–13434. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Liu, Y.; Ning, H.; Lei, J.; Hu, G. Synthesis, structure and properties of imidazolium-based energetic ionic liquids. RSC Adv. 2017, 7, 33231–33240. [Google Scholar] [CrossRef] [Green Version]
- Chiou, J.Y.Z.; Chen, J.N.; Lei, J.S.; Lin, I.J.B. Ionic liquid crystals of imidazolium salts with a pendant hydroxyl group. J. Mater. Chem. 2006, 16, 2972. [Google Scholar] [CrossRef]
- Getsis, A.; Mudring, A.V. Imidazolium based ionic liquid crystals: structure, photophysical and thermal behaviour of [Cnmim]BrxH2O (n = 12, 14; x = 0, 1). Cryst. Res. Technol. 2008, 43, 1187–1196. [Google Scholar] [CrossRef]
- Wang, Y.; Voth, G.A. Unique Spatial Heterogeneity in Ionic Liquids. J. Am. Chem. Soc. 2005, 127, 12192–12193. [Google Scholar] [CrossRef]
- Luettmer-Strathmann, J. Two-chamber lattice model for thermodiffusion in polymer solutions. J. Chem. Phys. 2003, 119, 2892–2902. [Google Scholar] [CrossRef] [Green Version]
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, P. A note on the electrochemical nature of the thermoelectric power. Eur. Phys. J. Plus 2016, 131. [Google Scholar] [CrossRef] [Green Version]
- Borukhov, I.; Andelman, D.; Orland, H. Steric Effects in Electrolytes: A Modified Poisson-Boltzmann Equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef] [Green Version]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jackson, M.; Engel, R.R.; Vuong, L.T. Role of Heat Expansion with a Series of Ionic Liquids: The Case for Isochoric Thermoelectric Generators and Minimal Steric Repulsion. Entropy 2019, 21, 1086. https://doi.org/10.3390/e21111086
Jackson M, Engel RR, Vuong LT. Role of Heat Expansion with a Series of Ionic Liquids: The Case for Isochoric Thermoelectric Generators and Minimal Steric Repulsion. Entropy. 2019; 21(11):1086. https://doi.org/10.3390/e21111086
Chicago/Turabian StyleJackson, Marcus, Robert R. Engel, and Luat T. Vuong. 2019. "Role of Heat Expansion with a Series of Ionic Liquids: The Case for Isochoric Thermoelectric Generators and Minimal Steric Repulsion" Entropy 21, no. 11: 1086. https://doi.org/10.3390/e21111086
APA StyleJackson, M., Engel, R. R., & Vuong, L. T. (2019). Role of Heat Expansion with a Series of Ionic Liquids: The Case for Isochoric Thermoelectric Generators and Minimal Steric Repulsion. Entropy, 21(11), 1086. https://doi.org/10.3390/e21111086