Hypergraph Contextuality
Abstract
:1. Introduction
2. Results
2.1. Formalism
- 1.
- Every vertex belongs to at least one edge;
- 2.
- Every edge contains at least 2 vertices;
- 3.
- Edges that intersect each other in vertices contain at least m vertices, where .
- 1.
- No two vertices within any of its edges are both assigned the value 1;
- 2.
- In any of its edges, not all of the vertices are assigned the value 0.
2.2. KS vs. Operator Contextuality
- 1.
- No two orthogonal vectors are both assigned the value 1;
- 2.
- In any group of n mutually orthogonal vectors, not all of the vectors are assigned the value 0.
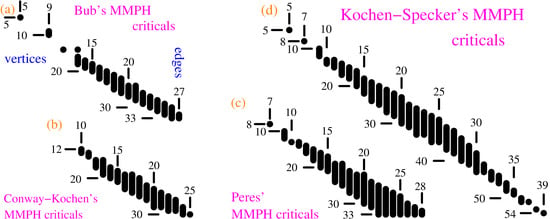
2.3. MMPH Masters
- (i)
- Peres wrote, “It can be shown that if a single ray is deleted from the set of 33, the contradiction disappears. It is so even if the deleted ray is not explicitly listed in Table 1.” ([61], L176, bottom paragraph)
- Ad (i)
- The first sentence is wrong because MMPH 33–40 set 123,345,47,79,92A,AC,C4,AF,5F,HJ, HL,H7M,NCO,OPQ,QRL,RT,TJ,JPV,VX,XR,Va,La,ce,cT1,cg,FXM,Mhi,ijg,jl,le,ehn,np,pj, nN,gN,t9,tlO,t5,ap1,1MO. is not critical as verified by STATES01. It is also not a KS set but only an MMPH non-binary set. The second sentence is conditionally correct because the full scale MMPH 57–40, 123,345,467,789,92A,ABC,CD4,AEF,5GF,HIJ,HKL,H7M,NCO, OPQ,QRL,RST,TUJ,JPV,VWX,XYR,VZa,Lba,cde,cT1,cfg,FXM,Mhi,ijg,jkl,lme,ehn,nop, pqj,nrN,gsN,tu9,tlO,tv5,ap1,1MO. is a critical KS set but only if assume that with the deleted ray we also delete the edge/triplet it belonged to. (This instance of Peres’ 57–40 KS set is isomorphic to the one given above; the sequence of characters is different due to a reshuffling by automated tools we used to obtain 33–40 as a subgraph of 57–40.
- (ii)
- Yu and Oh write, “The KS value assignments to the 13-ray set [13-16] are possible; i.e., no logical contradiction can be extracted by considering conditions 1 and 2 [of Theorem 1].” ([49], p. 3, left column, top)
- Ad (ii)
- The claim is provisionally correct, but not because “no logical contradiction can be extracted by considering conditions 1 and 2”—it can be extracted—in 13–16 it is impossible to assign 1s and 0s in such a way that conditions 1 and 2 are satisfied, and not because “value assignments to the 13-ray set are possible”—they are not possible; one cannot assign 1s and 0s to its rays in such a way that conditions 1 and 2 are satisfied—but because the 13–16 set is not a set of triplets and therefore does not satisfy the first part of the KS theorem.
2.4. Classes of MMPH Non-Binary Sets, Their Implementation, and Their Inequalities
3. Discussion
4. Methods
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| KS | Kochen-Specker |
| MMPH | McKay-Megill-Pavičić hypergraph |
Appendix A. ASCII Strings from MMPH Non-Binary Classes
Appendix A.1. Bub’s Class
Appendix A.2. Conway-Kochen’s Class
Appendix A.3. Peres’ Class
Appendix A.4. Kochen-Specker’ Class
References
- Cabello, A.; D’Ambrosio, V.; Nagali, E.; Sciarrino, F. Hybrid Ququart-Encoded Quantum Cryptography Protected by Kochen-Specker Contextuality. Phys. Rev. A 2011, 84, 030302. [Google Scholar] [CrossRef]
- Nagata, K. Kochen-Specker Theorem as a Precondition for Secure Quantum Key Distribution. Phys. Rev. A 2005, 72, 012325. [Google Scholar] [CrossRef]
- Howard, M.; Wallman, J.; Veitech, V.; Emerson, J. Contextuality Supplies the ‘Magic’ for Quantum Computation. Nature 2014, 510, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, S.D. Powered by Magic. Nature 2014, 510, 345–346. [Google Scholar] [CrossRef] [PubMed]
- Kurzyński, P.; Cabello, A.; Kaszlikowski, D. Fundamental Monogamy Relation between Contextuality and Nonlocality. Phys. Rev. Lett. 2014, 112, 100401. [Google Scholar] [CrossRef] [PubMed]
- Pavičić, M.; McKay, B.D.; Megill, N.D.; Fresl, K. Graph Approach to Quantum Systems. J. Math. Phys. 2010, 51, 102103. [Google Scholar] [CrossRef]
- Megill, N.D.; Pavičić, M. Kochen-Specker Sets and Generalized Orthoarguesian Equations. Ann. Henri Poinc. 2011, 12, 1417–1429. [Google Scholar] [CrossRef]
- Simon, C.; Żukowski, M.; Weinfurter, H.; Zeilinger, A. Feasible Kochen-Specker Experiment with Single Particles. Phys. Rev. Lett. 2000, 85, 1783–1786. [Google Scholar] [CrossRef] [PubMed]
- Michler, M.; Weinfurter, H.; Żukowski, M. Experiments towards Falsification of Noncontextual Hidden Variables. Phys. Rev. Lett. 2000, 84, 5457–5461. [Google Scholar] [CrossRef] [PubMed]
- Amselem, E.; Rådmark, M.; Bourennane, M.; Cabello, A. State-Independent Quantum Contextuality with Single Photons. Phys. Rev. Lett. 2009, 103, 160405. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.H.; Huang, Y.F.; Gong, Y.X.; Sun, F.W.; Zhang, Y.S.; Li, C.F.; Guo, G.C. Experimental Demonstration of Quantum Contextuality with Nonentangled Photons. Phys. Rev. A 2009, 80, 044101-1-4. [Google Scholar] [CrossRef]
- D’Ambrosio, V.; Herbauts, I.; Amselem, E.; Nagali, E.; Bourennane, M.; Sciarrino, F.; Cabello, A. Experimental Implementation of a Kochen-Specker Set of Quantum Tests. Phys. Rev. X 2013, 3, 011012. [Google Scholar] [CrossRef]
- Huang, Y.F.; Li, C.F.; Yong-Sheng Zhang, J.W.P.; Guo, G.C. Realization of All-or-nothing-type Kochen-Specker Experiment with Single Photons. Phys. Rev. Lett. 2002, 88, 240402. [Google Scholar]
- Huang, Y.F.; Li, C.F.; Zhang, Y.S.; Pan, J.W.; Guo, G.C. Experimental Test of the Kochen-Specker Theorem with Single Photons. Phys. Rev. Lett. 2003, 90, 250401. [Google Scholar] [CrossRef] [PubMed]
- Lapkiewicz, R.; Li, P.; Schaeff, C.; Langford, N.K.; Ramelow, S.; Wieśniak, M.; Zeilinger, A. Experimental Non-Classicality of an Indivisible Quantum System. Nature 2011, 474, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Zu, C.; Wang, Y.X.; Deng, D.L.; Chang, X.Y.; Liu, K.; Hou, P.Y.; Yang, H.X.; Duan, L.M. State-Independent Experimental Test of Quantum Contextuality in an Indivisible System. Phys. Rev. Lett. 2012, 109, 150401. [Google Scholar] [CrossRef] [PubMed]
- Cañas, G.; Etcheverry, S.; Gómez, E.S.; Saavedra, C.; Xavier, G.B.; Lima, G.; Cabello, A. Experimental Implementation of an Eight-Dimensional Kochen-Specker Set and Observation of Its Connection with the Greenberger-Horne-Zeilinger Theorem. Phys. Rev. A 2014, 90, 012119. [Google Scholar] [CrossRef]
- Cañas, G.; Arias, M.; Etcheverry, S.; Gómez, E.S.; Cabello, A.; Saavedra, C.; Xavier, G.B.; Lima, G. Applying the Simplest Kochen-Specker Set for Quantum Information Processing. Phys. Rev. Lett. 2014, 113, 090404. [Google Scholar] [CrossRef] [PubMed]
- Zhan, X.; Zhang, X.; Li, J.; Zhang, Y.; Sanders, B.C.; Xue, P. Realization of the Contextuality-Nonlocality Tradeoff with a Qubit-Qutrit Photon Pair. Phys. Rev. Lett. 2016, 116, 090401. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zeng1, Q.; Song, X.; Zhang, X. Experimental Contextuality in Classical Light. Sci. Rep. 2017, 7, 44467. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zeng, Q.; Zhang, X.; Chen, T.; Zhang, X. State-Independent Contextuality in Classical Light. 2019, in press. [Google Scholar]
- Frustaglia, D.; Baltanás, J.P.; Velázquez-Ahumada, M.C.; Fernández-Prieto, A.; Lujambio, A.; Losada, V.; Freire, M.J.; Cabello, A. Classical Physics and the Bounds of Quantum Correlations. Phys. Rev. Lett. 2016, 116, 250404. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.; Xu, H.; Xie, J.; Zhang, H.; Smith, B.J.; Kim, M.S.; Zhang, L. Experimental Test of Contextuality in Quantum and Classical Systems. Phys. Rev. Lett. 2004, 122, 080401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasegawa, Y.; Loidl, R.; Badurek, G.; Baron, M.; Rauch, H. Quantum Contextuality in a Single-Neutron Optical Experiment. Phys. Rev. Lett. 2006, 97, 230401. [Google Scholar] [CrossRef] [PubMed]
- Cabello, A.; Filipp, S.; Rauch, H.; Hasegawa, Y. Proposed Experiment for Testing Quantum Contextuality with Neutrons. Phys. Rev. Lett. 2008, 100, 130404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartosik, H.; Klepp, J.; Schmitzer, C.; Sponar, S.; Cabello, A.; Rauch, H.; Hasegawa, Y. Experimental Test of Quantum Contextuality in Neutron Interferometry. Phys. Rev. Lett. 2009, 103, 040403. [Google Scholar] [CrossRef] [PubMed]
- Kirchmair, G.; Zähringer, F.; Gerritsma, R.; Kleinmann, M.; Gühne, O.; Cabello, A.; Blatt, R.; Roos, C.F. State-Independent Experimental Test of Quantum Contextuality. Nature 2009, 460, 494–497. [Google Scholar] [CrossRef]
- Moussa, O.; Ryan, C.A.; Cory, D.G.; Laflamme, R. Testing Contextuality on Quantum Ensembles with One Clean Qubit. Phys. Rev. Lett. 2010, 104, 160501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jerger, M.; Reshitnyk, Y.; Oppliger, M.; Potočnik, A.; Mondal, M.; Wallraff, A.; Goodenough, K.; Wehner, S.; Juliusson, K.; Langford, N.K.; et al. Contextuality without Nonlocality in a Superconducting Quantum System. Nat. Commun. 2016, 7, 12930. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrett, J.; Kent, A. Noncontextuality, Finite Precision Measurement and the Kochen-Specker. Stud. Hist. Philos. Mod. Phys. 2004, 35, 151–176. [Google Scholar] [CrossRef] [Green Version]
- Kunjwal, R.; Spekkens, R.W. From the Kochen-Specker Theorem to Noncontextuality Inequalities without Assuming Determinism. Phys. Rev. Lett. 2015, 115, 110403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kunjwal, R. Hypergraph Framework for Irreducible Noncontextuality Inequalities from Logical Proofs of the Kochen-Specker Theorem. arXiv 2018, arXiv:1805.02083. Available online: https://arxiv.org/abs/1805.02083 (accessed on 12 November 2019).
- Bengtsson, I.; Blanchfield, K.; Cabello, A. A Kochen–Specker Inequality from a SIC. Phys. Lett. A 2012, 376, 374–376. [Google Scholar] [CrossRef] [Green Version]
- Cabello, A.; Estebaranz, J.M.; García-Alcaine, G. Bell-Kochen-Specker Theorem: A Proof with 18 Vectors. Phys. Lett. A 1996, 212, 183–187. [Google Scholar] [CrossRef] [Green Version]
- Pavičić, M.; Merlet, J.P.; McKay, B.D.; Megill, N.D. Kochen-Specker Vectors. J. Phys. A 2005, 38, 1577–1592. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. Critical Noncolorings of the 600-Cell Proving the Bell-Kochen-Specker Theorem. J. Phys. A 2010, 43, 105304. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K. Parity Proofs of the Kochen-Specker Theorem Based on 60 Complex Rays in Four Dimensions. J. Phys. A 2011, 44, 505303. [Google Scholar] [CrossRef] [Green Version]
- Megill, N.D.; Fresl, K.; Waegell, M.; Aravind, P.K.; Pavičić, M. Probabilistic Generation of Quantum Contextual Sets. Phys. Lett. A 2011, 375, 3419–3424. [Google Scholar] [CrossRef] [Green Version]
- Pavičić, M.; Megill, N.D.; Aravind, P.K.; Waegell, M. New Class of 4-Dim Kochen-Specker Sets. J. Math. Phys. 2011, 52, 022104. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K.; Megill, N.D.; Pavičić, M. Parity Proofs of the Bell-Kochen-Specker Theorem Based on the 600-cell. Found. Phys. 2011, 41, 883–904. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K. Proofs of Kochen-Specker Theorem Based on a System of Three Qubits. J. Phys. A 2012, 45, 405301. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K. Proofs of the Kochen-Specker Theorem Based on the N-Qubit Pauli Group. Phys. Rev. A 2013, 88, 012102. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K. Parity Proofs of the Kochen-Specker Theorem Based on 120-Cell. Found. Phys. 2014, 44, 1085–1095. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K. Parity Proofs of the Kochen-Specker Theorem Based on the Lie Algebra E8. J. Phys. A 2015, 48, 225301. [Google Scholar] [CrossRef] [Green Version]
- Waegell, M.; Aravind, P.K. The Penrose Dodecahedron and the Witting Polytope Are Identical in . Phys. Lett. A 2017, 381, 1853–1857. [Google Scholar] [CrossRef] [Green Version]
- Pavičić, M. Arbitrarily Exhaustive Hypergraph Generation of 4-, 6-, 8-, 16-, and 32-Dimensional Quantum Contextual Sets. Phys. Rev. A 2017, 95, 062121. [Google Scholar] [CrossRef] [Green Version]
- Pavičić, M.; Megill, N.D. Vector Generation of Quantum Contextual Sets in Even Dimensional Hilbert Spaces. Entropy 2018, 20, 928. [Google Scholar] [CrossRef] [Green Version]
- Pavičić, M.; Waegel, M.; Megill, N.D.; Aravind, P. Automated Generation of Kochen-Specker Sets. Sci. Rep. 2019, 9, 6765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, S.; Oh, C.H. State-Independent Proof of Kochen-Specker Theorem with 13 Rays. Phys. Rev. Lett. 2012, 108, 030402. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.P.; Chen, J.L.; Su, H.Y. State-independent contextuality sets for a qutrit. Phys. Lett. A 2015, 379, 1868–1870. [Google Scholar] [CrossRef] [Green Version]
- Ramanathan, R.; Horodecki, P. Necessary and Sufficient Condition for State-Independent Contextual Measurement Scenarios. Phys. Rev. Lett. 2014, 112, 040404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cabello, A.; Kleinmann, M.; Budroni, C. Necessary and Sufficient Condition for Quantum State-Independent Contextuality. Phys. Rev. Lett. 2014, 114, 250402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klyachko, A.A.; Can, M.A.; Binicioğlu, S.; Shumovsky, A.S. Simple Test for Hidden Variables in Spin-1 Systems. Phys. Rev. A 2008, 101, 020403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurzyński, P.; Ramanathan, R.; Kaszlikowski, D. Entropic Test of Quantum Contextuality. Phys. Rev. Lett. 2012, 109, 020404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braunstein, S.L.; Caves, C.M. Information- Theoretic Bell Inequalities. Phys. Rev. Lett. 1988, 61, 662–665. [Google Scholar] [CrossRef] [PubMed]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- McKay, B.D.; Megill, N.D.; Pavičić, M. Algorithms for Greechie Diagrams. Int. J. Theor. Phys. 2000, 39, 2381–2406. [Google Scholar] [CrossRef]
- Pavičić, M.; Megill, N.D.; Merlet, J.P. New Kochen-Specker Sets in Four Dimensions. Phys. Lett. A 2010, 374, 2122–2128. [Google Scholar] [CrossRef] [Green Version]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885–893. [Google Scholar] [CrossRef]
- Zimba, J.; Penrose, R. On Bell Non-Locality without Probabilities: More Curious Geometry. Stud. Hist. Phil. Sci. 1993, 24, 697–720. [Google Scholar] [CrossRef]
- Peres, A. Two Simple Proofs of the Bell-Kochen-Specker Theorem. J. Phys. A 1991, 24, L175–L178. [Google Scholar] [CrossRef]
- Bengtsson, I. Gleason, Kochen-Specker, and a Competition that Never Was. In Proceedings of the AIP, Vaxjo, Sweden, 11–14 June 2012; Volume 1508, pp. 125–135. [Google Scholar]
- Larsson, J.Å. A Kochen-Specker Inequality. Europhys. Lett. 2002, 58, 799–805. [Google Scholar] [CrossRef]
- Held, C. Kochen-Specker Theorem. In Compendium of Quantum Physics; Greenberger, D., Hentschel, K., Weinert, F., Eds.; Springer: New York, NY, USA, 2009; pp. 331–335. [Google Scholar]
- Ruuge, A.E. New Examples of Kochen–Specker-Type Configurations on Three Qubits. J. Phys. A 2012, 45, 465304. [Google Scholar] [CrossRef]
- Cabello, A.; Amselem, E.; Blanchfield, K.; Bourennane, M.; Bengtsson, I. Proposed Experiments of Qutrit State-Independent Contextuality and Two-Qutrit Contextuality-Based Nonlocality. Phys. Rev. A 2012, 85, 032108. [Google Scholar] [CrossRef] [Green Version]
- Kleinmann, M.; Budroni, C.; Larsson, J.Å.; Gühne, O.; Cabello, A. Optimal Inequalities for State-Independent Contextuality. Phys. Rev. Lett. 2012, 109, 250402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clifton, R. Getting Contextual and Nonlocal Elements-of-Reality the Easy Way. Am. J. Phys. 1993, 61, 443–447. [Google Scholar] [CrossRef]
- Svozil, K. Quantum Logic; Discrete Mathematics and Theoretical Computer Science; Springer: New York, NY, USA, 1998. [Google Scholar]
- Held, C. The Kochen-Specker Theorem. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2018; Available online: https://plato.stanford.edu/archives/spr2018/entries/kochen-specker (accessed on 12 November 2019).
- Bub, J. Schütte’s Tautology and the Kochen-Specker Theorem. Found. Phys. 1996, 26, 787–806. [Google Scholar] [CrossRef]
- Cabello, A.; Severini, S.; Winter, A. Graph-Theoretic Approach to Quantum Correlations. Phys. Rev. Lett. 2014, 112, 040401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cabello, A. Quantum Correlations from Simple Assumptions. Phys. Rev. A 2019, 100, 032120. [Google Scholar] [CrossRef] [Green Version]
- Pavičić, M.; Megill, N.D. Quantum Logic and Quantum Computation. In Handbook of Quantum Logic and Quantum Structures; Engesser, K., Gabbay, D., Lehmann, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Chapter Quantum Structures; pp. 751–787. [Google Scholar]
- Megill, N.D.; Pavičić, M. New Classes of Kochen-Specker Contextual Sets (Invited Talk). In Proceedings of the 40th MIPRO Convention, Opatija, Croatia, 22–26 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 195–200, ISBN 9781509049691. [Google Scholar]






© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavičić, M. Hypergraph Contextuality. Entropy 2019, 21, 1107. https://doi.org/10.3390/e21111107
Pavičić M. Hypergraph Contextuality. Entropy. 2019; 21(11):1107. https://doi.org/10.3390/e21111107
Chicago/Turabian StylePavičić, Mladen. 2019. "Hypergraph Contextuality" Entropy 21, no. 11: 1107. https://doi.org/10.3390/e21111107
APA StylePavičić, M. (2019). Hypergraph Contextuality. Entropy, 21(11), 1107. https://doi.org/10.3390/e21111107