Exploring Entropy Measurements to Identify Multi-Occupancy in Activities of Daily Living
Abstract
:1. Introduction
2. Related Work
2.1. HAR in Multi-Occupancy Environments
2.2. Data Association in Multi-Occupancy Environments
3. Methodology
- In the first phase, the sensor data representing ADL in a multi-occupancy environment is collected. We are primarily concentrating on the movement data representing the occupancy of different areas in a home environment. Without loss of generality, data gathered from other sensors, including door entry sensors, could also be used. The required numerical features to be used for calculating the sequences of the input vector are extracted from the raw data. The values of this vector are used as inputs to the entropy measures. The selected features representing the ADL from the sensor data are: the start time of entering each location (room), the time spent in each room, and the transitions from one room to another inside the house. The example provided in Section 5.2 will elaborate on the details of these features.
- In the second phase of the proposed process, different entropy measures are applied to the vector sequences to measure the activity level of multi-occupancy in the home environment.
- In the third phase, the standard deviation of the entropy measures is used to decide whether there is a visitor to the home environment.
4. Entropy Measures
4.1. Approximate Entropy (ApEn)
4.2. Sample Entropy (SampEn)
4.3. Fuzzy Entropy (FuzzyEn)
5. Data Sources and Preprocessing
5.1. Datasets
5.2. Data Preprocessing
6. Experimental Results and Analysis
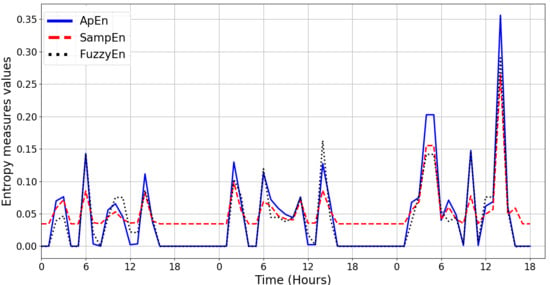
6.1. Experiment with Dataset A and Results
- True Positive is a set of data that contains a visitor event and was correctly classified as a visitor event.
- False Positive is a set of data that does not contain a visitor event, but it was incorrectly classified as a visitor event.
- True Negative is a set of data that does not contain a visitor event and it was correctly classified as a non-visitor event.
- False Negative is a set of data that contains a visitor event and it was incorrectly classified as a non-visitor event.
6.2. Experiment with Dataset B and Results
6.3. Robust Analysis
6.4. Comparison with Existing Modelling Techniques
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ADL | Activities of Daily Living |
| ApEn | Approximate Entropy |
| CHMM | Coupled Hidden Markov Model |
| CRF | Conditional Random Field |
| DBN | Dynamic Bayesian Network |
| FHMM | Factorial Hidden Markov Model |
| FuzzyEn | Fuzzy Entropy |
| GMM | Gaussian Mixture Models |
| HAR | Human Activity Recognition |
| HMM | Hidden Markov Model |
| IDT | Incremental Decision Trees |
| IM | Indoor Mobility |
| KNN | K-Nearest Neighbor |
| MCMC | Markov chain Monte Carlo |
| MLP | Multi-Layer Perceptron |
| MMPP | Markov Modulated Poisson Process |
| NBC | Naive Bayes Classifier |
| PIR | Passive Infra-Red Motion Sensor |
| RF | Random Forest |
| SampEn | Sample Entropy |
| SVM | Support Vector Machines |
| TDNN | Time-Delay Neural Network |
References
- Barsocchi, P.; Cimino, M.G.; Ferro, E.; Lazzeri, A.; Palumbo, F.; Vaglini, G. Monitoring elderly behavior via indoor position-based stigmergy. Pervasive Mob. Comput. 2015, 23, 26–42. [Google Scholar] [CrossRef]
- Tan, T.H.; Gochoo, M.; Jean, F.R.; Huang, S.C.; Kuo, S.Y. Front-door event classification algorithm for elderly people living alone in smart house using wireless binary sensors. IEEE Access 2017, 5, 10734–10743. [Google Scholar]
- Khan, S.S.; Karg, M.E.; Hoey, J.; Kulic, D. Towards the detection of unusual temporal events during activities using hmms. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; pp. 1075–1084. [Google Scholar]
- Aicha, A.N.; Englebienne, G.; Kröse, B. Unsupervised visit detection in smart homes. Pervasive Mob. Comput. 2017, 34, 157–167. [Google Scholar] [CrossRef]
- Alemdar, H.; Ersoy, C. Multi-resident activity tracking and recognition in smart environments. J. Ambient Intell. Humaniz. Comput. 2017, 8, 513–529. [Google Scholar] [CrossRef]
- Mohamed, R.; Perumal, T.; Sulaiman, M.N.; Mustapha, N.; Manaf, S.A. Tracking and Recognizing the Activity of Multi Resident in Smart Home Environments. J. Telecommun. Electron. Comput. Eng. (JTEC) 2017, 9, 39–43. [Google Scholar]
- Benmansour, A.; Bouchachia, A.; Feham, M. Modeling interaction in multi-resident activities. Neurocomputing 2017, 230, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Emi, I.A.; Stankovic, J.A. SARRIMA: Smart ADL recognizer and resident identifier in multi-resident accommodations. In Proceedings of the Conference on Wireless Health, Bethesda, MD, USA, 14–16 October 2015; p. 4. [Google Scholar]
- Hao, J.; Bouzouane, A.; Gaboury, S. Recognizing multi-resident activities in non-intrusive sensor-based smart homes by formal concept analysis. Neurocomputing 2018, 318, 75–89. [Google Scholar] [CrossRef]
- Mokhtari, G.; Anvari-Moghaddam, A.; Zhang, Q.; Karunanithi, M. Multi-Residential Activity Labelling in Smart Homes with Wearable Tags Using BLE Technology. Sensors 2018, 18, 908. [Google Scholar] [CrossRef]
- Benmansour, A.; Bouchachia, A.; Feham, M. Multioccupant activity recognition in pervasive smart home environments. ACM Comput. Surv. (CSUR) 2016, 48, 34. [Google Scholar] [CrossRef]
- Samarah, S.; Al Zamil, M.G.; Aleroud, A.F.; Rawashdeh, M.; Alhamid, M.F.; Alamri, A. An Efficient Activity Recognition Framework: Toward Privacy-Sensitive Health Data Sensing. IEEE Access 2017, 5, 3848–3859. [Google Scholar] [CrossRef]
- Kim, Y.; An, J.; Lee, M.; Lee, Y. An Activity-Embedding Approach for Next-Activity Prediction in a Multi-User Smart Space. In Proceedings of the 2017 IEEE International Conference on Smart Computing (SMARTCOMP), Hong Kong, China, 29–31 May 2017; pp. 1–6. [Google Scholar]
- Chen, R.; Tong, Y. A two-stage method for solving multi-resident activity recognition in smart environments. Entropy 2014, 16, 2184–2203. [Google Scholar] [CrossRef]
- Benmansour, A. Human Activity Recognition in the Context of Multi-Occupant Smart Homes. Ph.D. Thesis, University of Abou Bekr Belkaïd, Tlemcen, Algeria, 2016. [Google Scholar]
- Crandall, A.S.; Cook, D.J. Using a hidden markov model for resident identification. In Proceedings of the 2010 Sixth International Conference on Intelligent Environments, Kuala Lumpur, Malaysia, 19–21 July 2010; pp. 74–79. [Google Scholar]
- Tran, S.N.; Zhang, Q.; Karunanithi, M. On Multi-resident Activity Recognition in Ambient Smart-Homes. arXiv 2018, arXiv:1806.06611. [Google Scholar]
- Gu, T.; Wu, Z.; Wang, L.; Tao, X.; Lu, J. Mining emerging patterns for recognizing activities of multiple users in pervasive computing. In Proceedings of the 2009 6th Annual International Mobile and Ubiquitous Systems: Networking & Services, MobiQuitous, Toronto, ON, Canada, 13–16 July 2009; pp. 1–10. [Google Scholar]
- Wang, L.; Gu, T.; Tao, X.; Chen, H.; Lu, J. Recognizing multi-user activities using wearable sensors in a smart home. Pervasive Mob. Comput. 2011, 7, 287–298. [Google Scholar] [CrossRef]
- Reid, D. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Roy, N.; Misra, A.; Cook, D. Ambient and smartphone sensor assisted ADL recognition in multi-inhabitant smart environments. J. Ambient Intell. Humaniz. Comput. 2016, 7, 1–19. [Google Scholar] [CrossRef]
- Attal, F.; Mohammed, S.; Dedabrishvili, M.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. Physical human activity recognition using wearable sensors. Sensors 2015, 15, 31314–31338. [Google Scholar] [CrossRef]
- Hsu, K.C.; Chiang, Y.T.; Lin, G.Y.; Lu, C.H.; Hsu, J.Y.J.; Fu, L.C. Strategies for inference mechanism of conditional random fields for multiple-resident activity recognition in a smart home. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Córdoba, Spain, 1–4 June 2010; pp. 417–426. [Google Scholar]
- Cook, D.J.; Crandall, A.; Singla, G.; Thomas, B. Detection of social interaction in smart spaces. Cybern. Syst. Int. J. 2010, 41, 90–104. [Google Scholar] [CrossRef]
- Prossegger, M.; Bouchachia, A. Multi-resident activity recognition using incremental decision trees. In Adaptive and Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 182–191. [Google Scholar]
- Alemdar, H.; Ertan, H.; Incel, O.D.; Ersoy, C. ARAS human activity datasets in multiple homes with multiple residents. In Proceedings of the 7th International Conference on Pervasive Computing Technologies for Healthcare, Venice, Italy, 5–8 May 2013; pp. 232–235. [Google Scholar]
- Tunca, C.; Alemdar, H.; Ertan, H.; Incel, O.D.; Ersoy, C. Multimodal wireless sensor network-based ambient assisted living in real homes with multiple residents. Sensors 2014, 14, 9692–9719. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Cheng, Q.; Sheng, W. Human activity recognition via motion and vision data fusion. In Proceedings of the 2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2010; pp. 332–336. [Google Scholar]
- Schumitsch, B.; Schwarz, H.; Wiegand, T. Optimization of transform coefficient selection and motion vector estimation considering interpicture dependencies in hybrid video coding. In Image and Video Communications and Processing 2005; International Society for Optics and Photonics: San Jose, CA, USA, 2005; Volume 5685, pp. 327–335. [Google Scholar]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Ocean. Eng. 1983, 8, 173–184. [Google Scholar] [CrossRef]
- Han, M.; Xu, W.; Tao, H.; Gong, Y. An algorithm for multiple object trajectory tracking. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 1, p. I. [Google Scholar]
- Oh, S.; Russell, S.; Sastry, S. Markov chain Monte Carlo data association for general multiple-target tracking problems. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; Volume 1, pp. 735–742. [Google Scholar]
- Petersen, J.; Larimer, N.; Kaye, J.A.; Pavel, M.; Hayes, T.L. SVM to detect the presence of visitors in a smart home environment. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 5850–5853. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Roy, N.; Misra, A.; Cook, D. Infrastructure-assisted smartphone-based ADL recognition in multi-inhabitant smart environments. In Proceedings of the 2013 IEEE International Conference on Pervasive Computing and Communications (PerCom), San Diego, CA, USA, 18–22 March 2013; pp. 38–46. [Google Scholar]
- Mohamed, R.; Perumal, T.; Sulaiman, M.N.; Mustapha, N. Multi Resident Complex Activity Recognition in Smart Home: A Literature Review. Int. J. Smart Home 2017, 11, 21–32. [Google Scholar] [CrossRef]
- W.S. University: CASAS Smart Home Project. Available online: http://ailab.eecs.wsu.edu/casas/ (accessed on 18 April 2019).
- Chiang, Y.T.; Hsu, K.C.; Lu, C.H.; Fu, L.C.; Hsu, J.Y.J. Interaction models for multiple-resident activity recognition in a smart home. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3753–3758. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Contributions to the Theory of Statistics, Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1. [Google Scholar]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using fuzzyen, apen, and sampen. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Tibdewal, M.N.; Dey, H.R.; Mahadevappa, M.; Ray, A.; Malokar, M. Multiple entropies performance measure for detection and localization of multi-channel epileptic EEG. Biomed. Signal Process. Control 2017, 38, 158–167. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Li, W.; Ming, D.; Xu, R.; Ding, H.; Qi, H.; Wan, B. Research on visual attention classification based on EEG entropy parameters. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Beijing, China, 26–31 May 2012; pp. 1553–1556. [Google Scholar]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Realgames. HOME I/O Smart Home Automation Simulation. Available online: https://realgames.co/home-io/ (accessed on 24 June 2018).
- Dheeru, D.; Karra Taniskidou, E. UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets/Activities+of+Daily+Living+%28ADLs%29+Recognition+Using+Binary+Sensors (accessed on 18 April 2019).
- Time Series Entropy Measures Implemented With Numpy. Available online: https://github.com/ixjlyons/entro-py/blob/master/entropy.py (accessed on 30 July 2018).
- Chernbumroong, S.; Lotfi, A.; Langensiepen, C. Prediction of mobility entropy in an Ambient Intelligent environment. In Proceedings of the 2014 IEEE Symposium on Intelligent Agents (IA), Orlando, FL, USA, 9–12 December 2014; pp. 65–72. [Google Scholar]






| Reference | Type of Sensors | Data Association | Approach | Overall Accuracy |
|---|---|---|---|---|
| [4] | Ambient sensors | yes | Markov Modulated Poisson Process (MMPP) | 82.3% |
| [5] | Ambient sensors | no | Factorial Hidden Markov Model (FHMM) and Nonlinear Bayesian Tracking | 64% |
| [20] | Motion sensor | yes | Finite-set statistics (FISST) and Bayesian filtering | - |
| [21] | Ambient and smartphone sensor | no | Coupled Hidden Markov Model (CHMM) and HMM | 70% |
| [22] | Wearable sensors | no | K-NN, SVM, GMM and RF | - |
| [23] | Infrastructure | yes | Conditional Random Field (CRF) | 81.3% |
| [24] | Infrastructure | yes | 2 HMMs | 84% |
| [25] | Infrastructure | no | Incremental Decision Trees (IDT) | 40% |
| [14,26] | Infrastructure | yes | HMM and CRF | - |
| [27] | Infrastructure | yes | HMM, DT, KNN. TDNN and MLP | 84.6% |
| [28] | Motion sensor and wearable | no | Bayesian framework | 80.2% |
| [29] | Video encoder | no | Linear Signal Model for Hybrid and Video Decoding | 90% |
| [30] | Passive sonar | yes | The probabilistic data association (PDA) | 85% |
| [31] | CCTV cameras | no | HMM | 98.3% |
| [32] | Motion sensor | yes | Markov chain Monte Carlo (MCMC) | 82% |
| [33] | Passive sonar | no | SVM | 83.5% |
| Start Time | Duration (min) | Location | Encoded Number of Each Location |
|---|---|---|---|
| 09:00:01 | 5 | Bedroom | 3 |
| 09:05:22 | 1 | Corridor | 9 |
| 09:06:00 | 4 | Living room | 1 |
| 09:06:00 | 4 | Bathroom | 5 |
| 09:09:59 | 1 | Corridor | 9 |
| 09:11:00 | 49 | Living room | 1 |
| 10:00:00 | 6 | Kitchen | 7 |
| Entropy Measures | Calculation Period of 120 Min | Calculation Period of 60 Min | Calculation Period of 15 Min | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | Accuracy | Precision | Recall | Accuracy | Precision | Recall | |
| ApEn | 96.5 | 100 | 66.6 | 100 | 100 | 100 | 85.3 | 35 | 69.2 |
| SampEn | 86.6 | 50 | 66.6 | 96.4 | 75 | 75 | 86 | 29.3 | 66.6 |
| FuzzyEn | 96.5 | 100 | 66.6 | 100 | 100 | 100 | 87.5 | 38.2 | 73.6 |
| Entropy Measures | Calculation Period of 120 Min | Calculation Period of 60 Min | Calculation Period of 15 Min | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Precision | Recall | Accuracy | Precision | Recall | Accuracy | Precision | Recall | |
| ApEn | 96.4 | 100 | 57.1 | 99.4 | 100 | 87.5 | 82.4 | 8.6 | 71.4 |
| SampEn | 96.4 | 83.3 | 71.4 | 97 | 61.5 | 100 | 87.9 | 11.4 | 71.4 |
| FuzzyEn | 98.8 | 100 | 85.7 | 100 | 100 | 100 | 85.4 | 9.6 | 71.4 |
| m⇒ | 1 | 2 | 3 | 6 | 10 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| r⇓ | Precision (%) | Recall (%) | Precision (%) | Recall (%) | Precision (%) | Recall (%) | Precision (%) | Recall (%) | Precision (%) | Recall (%) |
| 0.2 | 100 | 83 | 100 | 100 | 33.3 | 83.3 | 16.6 | 50 | 10 | 50 |
| 0.6 | 100 | 83 | 100 | 100 | 33.3 | 83.3 | 16.6 | 50 | 10 | 50 |
| 1 | 100 | 83 | 100 | 100 | 33.3 | 83.3 | 16.16 | 50 | 10 | 50 |
| 1.8 | 100 | 83 | 100 | 100 | 33.3 | 83.3 | 16.6 | 50 | 10 | 50 |
| 2 | 23.5 | 66.6 | 25 | 66.6 | 23.5 | 66.6 | 14 | 50 | 8 | 33 |
| 3 | 23.5 | 66.6 | 25 | 66.6 | 23.5 | 66.6 | 14 | 50 | 8 | 33 |
| 5 | 14.2 | 50 | 11.1 | 50 | 10.7 | 50 | 7.5 | 33 | 6 | 33 |
| Results | ApEn | SampEn | FuzzyEn | Shifting Time | Overlapping (x) % |
|---|---|---|---|---|---|
| Accuracy | 99.4 | 97 | 100 | 0 min | |
| Precision | 100 | 61.5 | 100 | ||
| Recall | 87.5 | 100 | 100 | ||
| Accuracy | 94 | 95.5 | 96.4 | 15 min | |
| Precision | 50 | 56.2 | 62.5 | ||
| Recall | 80 | 90 | 100 | ||
| Accuracy | 88 | 90.4 | 86.9 | 30 min | |
| Precision | 30 | 35.7 | 27.2 | ||
| Recall | 50 | 41.6 | 50 | ||
| Accuracy | 87.5 | 90.5 | 91.6 | 45 min | |
| Precision | 26.2 | 33.3 | 39 | ||
| Recall | 60 | 60 | 70 |
| Approach | Accuracy | Precision | Recall |
|---|---|---|---|
| ApEn | 99.4% | 100% | 87.5% |
| SampEn | 97% | 61.5% | 100% |
| FuzzyEn | 100% | 100% | 100% |
| SVM | 82.2% | 70.8% | 72.8% |
| IM | 93.5% | 88% | 80% |
| MMPP | 78.6 | 75.2% | 78.4% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howedi, A.; Lotfi, A.; Pourabdollah, A. Exploring Entropy Measurements to Identify Multi-Occupancy in Activities of Daily Living. Entropy 2019, 21, 416. https://doi.org/10.3390/e21040416
Howedi A, Lotfi A, Pourabdollah A. Exploring Entropy Measurements to Identify Multi-Occupancy in Activities of Daily Living. Entropy. 2019; 21(4):416. https://doi.org/10.3390/e21040416
Chicago/Turabian StyleHowedi, Aadel, Ahmad Lotfi, and Amir Pourabdollah. 2019. "Exploring Entropy Measurements to Identify Multi-Occupancy in Activities of Daily Living" Entropy 21, no. 4: 416. https://doi.org/10.3390/e21040416
APA StyleHowedi, A., Lotfi, A., & Pourabdollah, A. (2019). Exploring Entropy Measurements to Identify Multi-Occupancy in Activities of Daily Living. Entropy, 21(4), 416. https://doi.org/10.3390/e21040416