Spectral Structure and Many-Body Dynamics of Ultracold Bosons in a Double-Well
Abstract
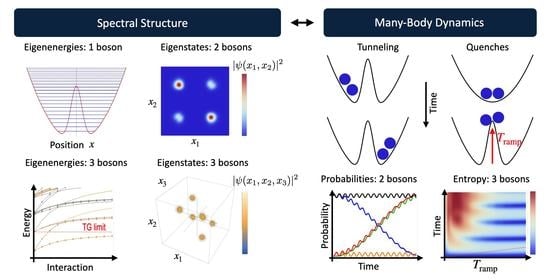
:1. Introduction
2. Hamiltonian and Methods
2.1. Hamiltonian of Trapped Interacting Bosons
2.2. Numerical Methods and Observables
3. Structure of Spectrum and Eigenstates
3.1. Few-Body Excitation Spectra
3.2. Eigenstate Structure and Few-Body Correlations
4. Dynamics in the Double-Well
4.1. Static Potential: Two-Body Excited State Dynamics
4.2. Time-Dependent Double-Well Potential: From Few- to Many-Body Dynamics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Fourier Grid Hamiltonian Method
Appendix B. Bose–Hubbard Model in the Continuum
Appendix C. Multiconfigurational Time-Dependent Hartree Method for Indistinguishable Particles
References
- Serwane, F.; Zürn, G.; Lompe, T.; Ottenstein, T.; Wenz, A.; Jochim, S. Deterministic preparation of a tunable few-fermion system. Science 2011, 332, 336–338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murmann, S.; Bergschneider, A.; Klinkhamer, V.M.; Zürn, G.; Lompe, T.; Jochim, S. Two Fermions in a Double Well: Exploring a Fundamental Building Block of the Hubbard Model. Phys. Rev. Lett. 2015, 114, 080402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morsch, O.; Oberthaler, M. Dynamics of Bose-Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct observation of tunneling and nonlinear self-trapping in a single bosonic Josephson junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef] [Green Version]
- Jördens, R.; Strohmaier, N.; Günter, K.; Moritz, H.; Esslinger, T. A Mott insulator of fermionic atoms in an optical lattice. Nature 2008, 455, 204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greiner, M.; Mandel, O.; Esslinger, T.; Hänsch, T.W.; Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 2002, 415, 39. [Google Scholar] [CrossRef]
- Bloch, I.; Greiner, M. Exploring quantum matter with ultracold atoms in optical lattices. Adv. At. Mol. Opt. Phys. 2005, 52, 1–47. [Google Scholar]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body Physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885. [Google Scholar] [CrossRef] [Green Version]
- Bloch, I. Quantum coherence and entanglement with ultracold atoms in optical lattices. Nature 2008, 453, 1016. [Google Scholar] [CrossRef]
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995–1001. [Google Scholar] [CrossRef] [Green Version]
- Schollwöck, U. The density-matrix renormalization group. Rev. Mod. Phys. 2005, 77, 259. [Google Scholar] [CrossRef] [Green Version]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef] [Green Version]
- Wall, M.L.; Carr, L.D. Out-of-equilibrium dynamics with matrix product states. New J. Phys. 2012, 14, 125015. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems. Phys. Rev. A 2008, 77, 033613. [Google Scholar] [CrossRef] [Green Version]
- Lode, A.U.J.; Lévêque, C.; Madsen, L.B.; Streltsov, A.I.; Alon, O.E. Colloquium: Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. Rev. Mod. Phys. 2020, 92, 011001. [Google Scholar] [CrossRef] [Green Version]
- Parker, J.; Doherty, B.; Meharg, K.; Taylor, K. Time delay between singly and doubly ionizing wavepackets in laser-driven helium. J. Phys. B At. Mol. Opt. Phys. 2003, 36, L393. [Google Scholar] [CrossRef]
- Buchleitner, A.; Kolovsky, A. Interaction-induced decoherence of atomic Bloch oscillations. Phys. Rev. Lett. 2003, 91, 253002. [Google Scholar] [CrossRef] [Green Version]
- Pasek, M.; Orso, G.; Delande, D. Anderson localization of ultracold atoms: Where is the mobility edge? Phys. Rev. Lett. 2017, 118, 170403. [Google Scholar] [CrossRef] [Green Version]
- Davies, E.B. Quantum Theory of Open Systems; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Alicki, R.; Lendi, K. Quantum Dynamical Semigroups and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gardiner, C.; Zoller, P. Quantum Noise: A Handbook of Markovian and non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Schlagheck, P.; Ullmo, D.; Urbina, J.D.; Richter, K.; Tomsovic, S. Enhancement of Many-Body Quantum Interference in Chaotic Bosonic Systems: The Role of Symmetry and Dynamics. Phys. Rev. Lett. 2019, 123, 215302. [Google Scholar] [CrossRef] [Green Version]
- Guhr, T.; Müller-Groeling, A.; Weidenmüller, H.A. Random-matrix theories in quantum physics: Common concepts. Phys. Rep. 1998, 299, 189–425. [Google Scholar] [CrossRef] [Green Version]
- Walschaers, M.; Kuipers, J.; Buchleitner, A. From many-particle interference to correlation spectroscopy. Phys. Rev. A 2016, 94, 020104. [Google Scholar] [CrossRef] [Green Version]
- Lindinger, J.; Buchleitner, A.; Rodriguez, A. Many-Body Multifractality throughout Bosonic Superfluid and Mott Insulator Phases. Phys. Rev. Lett. 2019, 122, 106603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lode, A.U.J.; Sakmann, K.; Alon, O.E.; Cederbaum, L.S.; Streltsov, A.I. Numerically exact quantum dynamics of bosons with time-dependent interactions of harmonic type. Phys. Rev. A 2012, 86, 063606. [Google Scholar] [CrossRef] [Green Version]
- Fasshauer, E.; Lode, A.U.J. Multiconfigurational time-dependent Hartree method for fermions: Implementation, exactness, and few-fermion tunneling to open space. Phys. Rev. A 2016, 93, 033635. [Google Scholar] [CrossRef] [Green Version]
- Walschaers, M.; Schlawin, F.; Wellens, T.; Buchleitner, A. Quantum transport on disordered and noisy networks: An interplay of structural complexity and uncertainty. Annu. Rev. Condens. Matter Phys. 2016, 7, 223–248. [Google Scholar] [CrossRef]
- Carnio, E.G.; Hine, N.D.; Römer, R.A. Resolution of the exponent puzzle for the Anderson transition in doped semiconductors. Phys. Rev. B 2019, 99, 081201. [Google Scholar] [CrossRef] [Green Version]
- Fölling, S.; Trotzky, S.; Cheinet, P.; Feld, M.; Saers, R.; Widera, A.; Müller, T.; Bloch, I. Direct observation of second-order atom tunnelling. Nature 2007, 448, 1029. [Google Scholar] [CrossRef] [Green Version]
- Milburn, G.; Corney, J.; Wright, E.M.; Walls, D. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318. [Google Scholar] [CrossRef] [Green Version]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S. Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 79, 4950. [Google Scholar] [CrossRef] [Green Version]
- Menotti, C.; Anglin, J.; Cirac, J.; Zoller, P. Dynamic splitting of a Bose-Einstein condensate. Phys. Rev. A 2001, 63, 023601. [Google Scholar] [CrossRef] [Green Version]
- Mahmud, K.W.; Perry, H.; Reinhardt, W.P. Quantum phase-space picture of Bose-Einstein condensates in a double well. Phys. Rev. A 2005, 71, 023615. [Google Scholar] [CrossRef] [Green Version]
- Salgueiro, A.; de Toledo Piza, A.; Lemos, G.; Drumond, R.; Nemes, M.; Weidemüller, M. Quantum dynamics of bosons in a double-well potential: Josephson oscillations, self-trapping and ultralong tunneling times. Eur. Phys. J. D 2007, 44, 537–540. [Google Scholar] [CrossRef] [Green Version]
- Murphy, D.; McCann, J.; Goold, J.; Busch, T. Boson pairs in a one-dimensional split trap. Phys. Rev. A 2007, 76, 053616. [Google Scholar] [CrossRef] [Green Version]
- Murphy, D.; McCann, J. Low-energy excitations of a boson pair in a double-well trap. Phys. Rev. A 2008, 77, 063413. [Google Scholar] [CrossRef] [Green Version]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Role of excited states in the splitting of a trapped interacting Bose-Einstein condensate by a time-dependent barrier. Phys. Rev. Lett. 2007, 99, 030402. [Google Scholar] [CrossRef] [Green Version]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Exact Quantum Dynamics of a Bosonic Josephson Junction. Phys. Rev. Lett. 2009, 103, 220601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zöllner, S.; Meyer, H.D.; Schmelcher, P. Ultracold few-boson systems in a double-well trap. Phys. Rev. A 2006, 74, 053612. [Google Scholar] [CrossRef] [Green Version]
- Zöllner, S.; Meyer, H.D.; Schmelcher, P. Excitations of few-boson systems in one-dimensional harmonic and double wells. Phys. Rev. A 2007, 75, 043608. [Google Scholar] [CrossRef] [Green Version]
- Zöllner, S.; Meyer, H.D.; Schmelcher, P. Tunneling dynamics of a few bosons in a double well. Phys. Rev. A 2008, 78, 013621. [Google Scholar] [CrossRef] [Green Version]
- Zöllner, S.; Meyer, H.D.; Schmelcher, P. Few-Boson dynamics in double wells: From single-atom to correlated pair tunneling. Phys. Rev. Lett. 2008, 100, 040401. [Google Scholar] [CrossRef] [Green Version]
- Theisen, M.; Streltsov, A.I. Many-body excitations and deexcitations in trapped ultracold bosonic clouds. Phys. Rev. A 2016, 94, 053622. [Google Scholar] [CrossRef] [Green Version]
- Dobrzyniecki, J.; Sowiński, T. Exact dynamics of two ultra-cold bosons confined in a one-dimensional double-well potential. Eur. Phys. J. D 2016, 70, 83. [Google Scholar] [CrossRef] [Green Version]
- Spagnolli, G.; Semeghini, G.; Masi, L.; Ferioli, G.; Trenkwalder, A.; Coop, S.; Landini, M.; Pezze, L.; Modugno, G.; Inguscio, M.; et al. Crossing over from attractive to repulsive interactions in a tunneling bosonic josephson junction. Phys. Rev. Lett. 2017, 118, 230403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parra-Murillo, C.A.; Madronero, J.; Wimberger, S. Two-band Bose-Hubbard model for many-body resonant tunneling in the Wannier-Stark system. Phys. Rev. A 2013, 88, 032119. [Google Scholar] [CrossRef] [Green Version]
- Kolovsky, A.R.; Buchleitner, A. Floquet-Bloch operator for the Bose-Hubbard model with static field. Phys. Rev. E 2003, 68, 056213. [Google Scholar] [CrossRef]
- Kolovsky, A.R.; Buchleitner, A. Quantum chaos in the Bose-Hubbard model. Europhys. Lett. 2004, 68, 632. [Google Scholar] [CrossRef] [Green Version]
- Lode, A.U.J. Multiconfigurational time-dependent Hartree method for bosons with internal degrees of freedom: Theory and composite fragmentation of multicomponent Bose-Einstein condensates. Phys. Rev. A 2016, 93, 063601. [Google Scholar] [CrossRef] [Green Version]
- Lode, A.U.J.; Tsatsos, M.C.; Fasshauer, E.; Lin, R.; Papariello, L.; Molignini, P.; Lévêque, C.; Weiner, S.E. MCTDH-X: The Time-Dependent Multiconfigurational Hartree for Indistinguishable Particles Software. 2020. Available online: http://ultracold.org (accessed on 24 March 2020).
- Nguyen, J.; Tsatsos, M.; Luo, D.; Lode, A.U.J.; Telles, G.; Bagnato, V.; Hulet, R. Parametric excitation of a Bose-Einstein condensate: From Faraday waves to granulation. Phys. Rev. X 2019, 9, 011052. [Google Scholar] [CrossRef] [Green Version]
- Olshanii, M. Atomic scattering in the presence of an external confinement and a gas of impenetrable bosons. Phys. Rev. Lett. 1998, 81, 938. [Google Scholar] [CrossRef] [Green Version]
- Hunn, S.; Zimmermann, K.; Hiller, M.; Buchleitner, A. Tunneling decay of two interacting bosons in an asymmetric double-well potential: A spectral approach. Phys. Rev. A 2013, 87, 043626. [Google Scholar] [CrossRef] [Green Version]
- Schäfer, F. Dynamics and Spectral Structure of Strongly Interacting Bosons in a Bouble Well. Master’s Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, March 2018. [Google Scholar] [CrossRef]
- Mack, H.; Freyberger, M. Dynamics of entanglement between two trapped atoms. Phys. Rev. A 2002, 66, 042113. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Zhou, D.L.; You, L. Entanglement between two interacting atoms in a one-dimensional harmonic trap. Phys. Rev. A 2006, 73, 012336. [Google Scholar] [CrossRef]
- Sowiński, T.; Brewczyk, M.; Gajda, M.; Rzążewski, K. Dynamics and decoherence of two cold bosons in a one-dimensional harmonic trap. Phys. Rev. A 2010, 82, 053631. [Google Scholar] [CrossRef] [Green Version]
- Ghirardi, G.; Marinatto, L. Entanglement and properties. Fortschritte der Physik 2003, 51, 379–387. [Google Scholar] [CrossRef] [Green Version]
- Ghirardi, G.; Marinatto, L. General criterion for the entanglement of two indistinguishable particles. Phys. Rev. A 2004, 70, 012109. [Google Scholar] [CrossRef] [Green Version]
- Ghirardi, G.; Marinatto, L. Criteria for the entanglement of composite systems with identical particles. Fortschritte der Physik 2004, 52, 1045–1051. [Google Scholar] [CrossRef] [Green Version]
- Benatti, F.; Floreanini, R.; Marzolino, U. Entanglement and squeezing with identical particles: Ultracold atom quantum metrology. J. Phys. B 2011, 44, 091001. [Google Scholar] [CrossRef] [Green Version]
- Tichy, M.C.; de Melo, F.; Kuś, M.; Mintert, F.; Buchleitner, A. Entanglement of identical particles and the detection process. Fortschritte der Physik 2013, 61, 225. [Google Scholar] [CrossRef]
- Hunn, S. Microscopic Theory of Decaying Many-Particle Systems. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg, Germany, September 2013. [Google Scholar]
- Busch, T.; Englert, B.G.; Rzażewski, K.; Wilkens, M. Two cold atoms in a harmonic trap. Found. Phys. 1998, 28, 549–559. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Reduced density matrices and coherence of trapped interacting bosons. Phys. Rev. A 2008, 78, 023615. [Google Scholar] [CrossRef]
- Sakmann, K.; Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. Universality of fragmentation in the Schrödinger dynamics of bosonic Josephson junctions. Phys. Rev. A 2014, 89, 023602. [Google Scholar] [CrossRef] [Green Version]
- Dobrzyniecki, J.; Sowiński, T. Effective two-mode description of a few ultra-cold bosons in a double-well potential. Phys. Lett. A 2018, 382, 394–399. [Google Scholar] [CrossRef] [Green Version]
- Dobrzyniecki, J.; Li, X.; Nielsen, A.E.; Sowiński, T. Effective three-body interactions for bosons in a double-well confinement. Phys. Rev. A 2018, 97, 013609. [Google Scholar] [CrossRef] [Green Version]
- Shin, Y.; Saba, M.; Pasquini, T.; Ketterle, W.; Pritchard, D.; Leanhardt, A. Atom interferometry with Bose-Einstein condensates in a double-well potential. Phys. Rev. Lett. 2004, 92, 050405. [Google Scholar] [CrossRef] [Green Version]
- Orzel, C.; Tuchman, A.; Fenselau, M.; Yasuda, M.; Kasevich, M. Squeezed states in a Bose-Einstein condensate. Science 2001, 291, 2386–2389. [Google Scholar] [CrossRef]
- Ebert, M.; Volosniev, A.; Hammer, H.W. Two cold atoms in a time-dependent harmonic trap in one dimension. Annalen der Physik 2016, 528, 693–704. [Google Scholar] [CrossRef] [Green Version]
- Streltsov, A.I.; Sakmann, K.; Alon, O.E.; Cederbaum, L.S. Accurate multi-boson long-time dynamics in triple-well periodic traps. Phys. Rev. A 2011, 83, 043604. [Google Scholar] [CrossRef] [Green Version]
- Alon, O.E. Analysis of a Trapped Bose–Einstein Condensate in Terms of Position, Momentum, and Angular-Momentum Variance. Symmetry 2019, 11, 1344. [Google Scholar] [CrossRef] [Green Version]
- Marston, C.C.; Balint-Kurti, G.G. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions. J. Chem. Phys. 1989, 91, 3571–3576. [Google Scholar] [CrossRef] [Green Version]
- Balint-Kurti, G.G.; Ward, C.L.; Marston, C.C. Two computer programs for solving the Schrödinger equation for bound-state eigenvalues and eigenfunctions using the Fourier grid Hamiltonian method. Comput. Phys. Commun. 1991, 67, 285–292. [Google Scholar] [CrossRef]
- Kahan, W. Pracniques: Further remarks on reducing truncation errors. Commun. ACM 1965, 8, 40. [Google Scholar] [CrossRef]
- Muth, D.; Fleischhauer, M.; Schmidt, B. Discretized versus continuous models of p-wave interacting fermions in one dimension. Phys. Rev. A 2010, 82, 013602. [Google Scholar] [CrossRef] [Green Version]
- Polizzi, E.; Kestyn, J. FEAST Eigenvalue Solver v3. 0 User Guide. arXiv 2012, arXiv:1203.4031. [Google Scholar]
- Polizzi, E. Density-matrix-based algorithm for solving eigenvalue problems. Phys. Rev. B 2009, 79, 115112. [Google Scholar] [CrossRef] [Green Version]
- Lode, A.U.J.; Bruder, C. Dynamics of Hubbard Hamiltonians with the multiconfigurational time-dependent Hartree method for indistinguishable particles. Phys. Rev. A 2016, 94, 013616. [Google Scholar] [CrossRef] [Green Version]
- Wells, T.; Lode, A.U.J.; Bagnato, V.S.; Tsatsos, M. Vortex reconnections in anisotropic trapped three-dimensional Bose–Einstein condensates. J. Low Temp. Phys. 2015, 180, 133–143. [Google Scholar] [CrossRef] [Green Version]
- Kramer, P.; Saraceno, M. Geometry of the Time-Dependent Variational Principle in Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Conte, D.; Lubich, C. An error analysis of the multi-configuration time-dependent Hartree method of quantum dynamics. ESAIM Math. Model. Numer. Anal. 2010, 44, 759–780. [Google Scholar] [CrossRef] [Green Version]
- Lin, R.; Molignini, P.; Papariello, L.; Tsatsos, M.C.; Leveque, C.; Weiner, S.E.; Fasshauer, E.; Chitra, R.; Lode, A.U.J. MCTDH-X: The multiconfigurational time-dependent Hartree method for indistinguishable particles software. Quantum Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Beck, M.H.; Jäckle, A.; Worth, G.A.; Meyer, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]














© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schäfer, F.; Bastarrachea-Magnani, M.A.; Lode, A.U.J.; de Parny, L.d.F.; Buchleitner, A. Spectral Structure and Many-Body Dynamics of Ultracold Bosons in a Double-Well. Entropy 2020, 22, 382. https://doi.org/10.3390/e22040382
Schäfer F, Bastarrachea-Magnani MA, Lode AUJ, de Parny LdF, Buchleitner A. Spectral Structure and Many-Body Dynamics of Ultracold Bosons in a Double-Well. Entropy. 2020; 22(4):382. https://doi.org/10.3390/e22040382
Chicago/Turabian StyleSchäfer, Frank, Miguel A. Bastarrachea-Magnani, Axel U. J. Lode, Laurent de Forges de Parny, and Andreas Buchleitner. 2020. "Spectral Structure and Many-Body Dynamics of Ultracold Bosons in a Double-Well" Entropy 22, no. 4: 382. https://doi.org/10.3390/e22040382
APA StyleSchäfer, F., Bastarrachea-Magnani, M. A., Lode, A. U. J., de Parny, L. d. F., & Buchleitner, A. (2020). Spectral Structure and Many-Body Dynamics of Ultracold Bosons in a Double-Well. Entropy, 22(4), 382. https://doi.org/10.3390/e22040382