Next Article in Journal
Identifying Stereoisomers by ab-initio Calculation of Secondary Isotope Shifts on NMR Chemical Shieldings
Next Article in Special Issue
Nonlinear Optical Molecular Switches for Alkali Ion Identification
Previous Article in Journal
Immunostimulatory Effects of Polysaccharides Isolated from Makgeolli (Traditional Korean Rice Wine)
Previous Article in Special Issue
C5-Azobenzene-substituted 2'-Deoxyuridine-containing Oligodeoxynucleotides for Photo-Switching Hybridization
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 19
Issue 4
10.3390/molecules19045278
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers

by
Alexander B. C. Deutman
,
Tim Woltinge
,
Jan M. M. Smits
,
René De Gelder
,
Johannes A. A. W. Elemans
,
Roeland J. M. Nolte
* and
Alan E. Rowan
Institute for Molecules and Materials, Radboud University Nijmegen, Heyendaalseweg 135, Nijmegen 6525 AJ, The Netherlands
*
Author to whom correspondence should be addressed.
Molecules 2014, 19(4), 5278-5300; https://doi.org/10.3390/molecules19045278
Submission received: 10 March 2014 / Revised: 14 April 2014 / Accepted: 17 April 2014 / Published: 23 April 2014
(This article belongs to the Special Issue Molecular Switches)
Browse Figures
Versions Notes

Abstract

:
The synthesis and switching properties of two “basket handle” porphyrin isomers is described. The cis-oriented meso-phenyl groups of these porphyrins are linked at their ortho-positons via benzocrown-ether-based spacers, which as a result of slow atropisomerization are located either on the same side of the porphyrin plane (cis), or on opposite sides (trans). In solution, the cis-linked isomer slowly isomerizes in the direction of the thermodynamically more stable trans-isomer. In the presence of viologen (N,N'-dialkyl-4,4'-bipyridinium) derivatives, which have different affinities for the two isomers, the isomerization equilibrium could be significantly influenced. In addition, the presence of these guests was found to enhance the rate of the switching process, which was suggested to be caused by favorable interactions between the positively charged guest and the crown ethers of the receptor, stabilizing the transition state energies of the isomerization reaction between the two isomers.

Graphical Abstract

1. Introduction

Host-guest chemistry provides a valuable platform for studying binding processes observed in nature with the help of relatively simple mimics. Many artificial receptors have been designed, displaying similar features as observed in natural host-guest systems, such as induced-fit binding [1,2,3,4], lock and key mechanisms [5], and cooperative binding effects [6,7,8,9,10,11,12]. Dynamic recognition processes, in which the guest influences the conformation of the receptor, play a crucial role in biological systems and are of particular importance for allosteric binding, regulation or feedback [13,14,15,16,17]. To date, there are a number of examples of artificial dynamic recognition systems that exhibit complexation-induced atropisomerism or conformational changes [18,19,20,21,22,23,24,25,26,27,28,29,30]. The vast majority of these studies, however, is focused on thermodynamic aspects of complex formation, whereas kinetic aspects, while being of significant importance for determining the actual binding mechanisms involved, are not explored. Houk et al. have convincingly demonstrated that the origin of binding affinities between guests and receptors (ranging from small synthetic cavitands to large proteins) are well-understood, and that enzymes do not show any special binding behaviour for their substrates when compared to artificial receptors [31]. This is a powerful reminder that the ability to catalyze reactions arises from transition state interactions and not from substrate binding. Therefore, in order to get a better understanding of the combination of interactions responsible for the nature of transition states in enzymatic systems, it is of key importance to also study the transition states of relatively simple artificial host-guest systems. However, for many of these systems the kinetics of the binding processes are simply too fast to be studied accurately with the help of general methods.
In order to gain detailed insight in the kinetic aspects of complexation-induced conformational changes of dynamic artificial receptors, we have designed a porphyrin-based receptor molecule that interconverts extremely slowly between two distinct conformational isomers. Thanks to this slow exchange, not only the guest-induced kinetics of interconversion between the two isomers could be studied accurately, but in addition also the binding affinities of each of the two isomers towards viologen (N,N'-dialkyl-4,4'-bipyridinium) guests could be determined. A complete kinetic and thermodynamic picture of a guest-induced “switching” was obtained, which revealed that the presence of guests not only influences the thermodynamic outcome, as expected on the basis of the obtained individual equilibrium constants, but also significantly influences the kinetics of the switching process.

2. Results and Discussion

2.1. Design

We decided to make use of the atropisomerization properties of ortho-meso-phenyl-substituted porphyrins in the design of the receptor. It is known that the restricted rotation of the aryl rings in many of such porphyrins can be extremely slow [32,33] (rates between 10−4 and 10−9 s−1 depending on the substitution pattern and metal ion present in the porphyrin), which often allows the isolation of the individual atropisomers. By appending two adjacent-linked binding pockets (“handles”) to the porphyrin ortho-phenyl positions, two so-called “basket handle” porphyrin [34,35,36,37,38,39,40] isomers (trans-linked S and cis-linked C; Scheme 1), which can interconvert slowly via atropizomerization, requiring the rotation around two aryl rings, were obtained By appending crown ether handles that are specifically designed for the complexation of viologen derivatives, the adjacent-linked “basket handle” porphyrins are expected to become excellent receptor molecules for these guests. The cis-linked isomer C was expected to have higher affinity for the viologen derivatives than trans-linked isomer S as a result of the interplay of two crown ether handles on the same side of the porphyrin plane in the former isomer. The addition of viologen derivatives should therefore result in the slow switching of the equilibrium in the direction of isomer C, a process that allows the accurate determination of both the thermodynamics and the kinetics involved.
Molecules 19 05278 g011 550
Scheme 1. Synthesis of basket handle isomers X, S and C.
Scheme 1. Synthesis of basket handle isomers X, S and C.
Molecules 19 05278 g011

2.2. Synthesis

A mixture of “basket handle” porphyrin isomers X, C and S (Scheme 1) was prepared in an overall yield of 52% by reacting ditosylate 1 [41] with 5,10,15,20-tetrakis(meso-o-hydroxyphenyl)porphyrin 2 [42] under basic conditions in DMF at 110 °C. The three different isomers could be separated by preparative TLC and were obtained in a ratio X:S:C = 4:8:1. The individual isomers were identified with the help of 1H-NMR spectroscopy in CDCl3 (Figure 1a), and in addition the X-Ray structure of the S-isomer was determined (Figure 1b). Isomer X has an S2 symmetry, and as a result the 1H-NMR spectrum revealed only four resonances for all the 32 crown ether protons H-3, H-4, H-5 and H-6, and one single resonance for the β-pyrrolic porphyrin protons. Isomers S and C have C2h and C2v symmetry, respectively, and as a result the crown ether proton resonances show AB-patterns in the 1H-NMR spectra and two distinct resonances for the β-pyrrolic protons. The resonances of the protons of the handles of S (H-1–H-6) are significantly shifted upfield in comparison to those of C, which indicates that they experience more shielding from the porphyrin ring-current. This can be understood since in S there is space to position both handles in the proximity of the porphyrin, whereas in C this is sterically impossible. Also the pyrrole NH resonances of S are shifted upfield compared to those of C, which suggests that the ring currents of the phenyl groups of the handles shield the center of the porphyrin more in S than in C. These combined observations indicate that, unlike in the X-ray structure of S in which the handles bend away from the porphyrin plane (Figure 1b), in solution they are on average folded over the porphyrin plane. This folding was confirmed by a 2D-ROESY NMR measurement which showed nOe contacts between the handle phenyl protons H-1 and H-2 and the β-pyrrole protons and H-10, respectively.
Molecules 19 05278 g001 550
Figure 1. (a) 1H-NMR spectra (400 MHz) of “basket handle” porphyrin isomers X, S and C in CDCl3 with proton assignments based on COSY and 2D-ROESY NMR experiments. See Scheme 1 for proton numbering. (b) X-ray structure of isomer S (protons have been omitted for clarity).
Figure 1. (a) 1H-NMR spectra (400 MHz) of “basket handle” porphyrin isomers X, S and C in CDCl3 with proton assignments based on COSY and 2D-ROESY NMR experiments. See Scheme 1 for proton numbering. (b) X-ray structure of isomer S (protons have been omitted for clarity).
Molecules 19 05278 g001

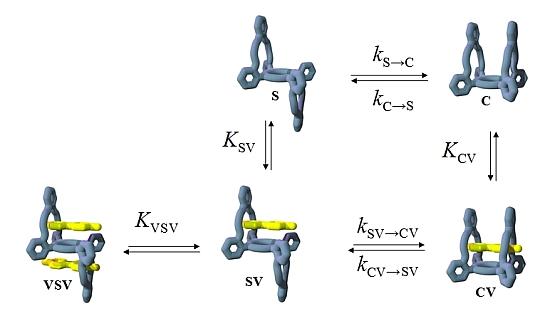
2.3. Isomerization

As observed in other adjacent-linked “basket handle” porphyrins [36] the adjacent-cis-linked isomer C and the adjacent-trans-linked isomer S slowly interconvert in time. Figure 2 reveals that upon standing, the resonances of S in the 1H-NMR spectra increase in intensity at the expense of those of C. Isomer S is thermodynamically significantly more stable than isomer C, since equilibrium is reached at a ratio of S/C = 7.6. This observation is in contrast with results in a previous report, in which the switching of a hexyl-bridged basket-handle porphyrin resulted in equimolar amounts of the adjacent-cis-linked and adjacent-trans-linked isomers at equilibrium [43], as would statistically be expected. The rate constants for the isomerization process (kC→S) could be simply determined by first order analysis of the decrease in the relative intensities [44] of the resonances of C in time.
The equilibrium constants (KS/C = [S]eq/[C]eq) were obtained at different temperatures from the ratio between S and C at equilibrium, after which the rate constant kS→C could be calculated indirectly from KS/C = kC→S/kS→C. Isomerization experiments in which the switching from S to C was monitored provided identical values for kS→C as were obtained by the indirect method via KS/C and kC→S. The calculated constants are presented in Table 1.
Molecules 19 05278 g002 550
Figure 2. Series of partial 400 MHz 1H-NMR spectra in time revealing the decrease in abundance of cis-linked isomer C in favor of the thermodynamically more stable trans-linked isomer S at 25 °C in CDCl3/CD3CN 1:1 (v/v).
Figure 2. Series of partial 400 MHz 1H-NMR spectra in time revealing the decrease in abundance of cis-linked isomer C in favor of the thermodynamically more stable trans-linked isomer S at 25 °C in CDCl3/CD3CN 1:1 (v/v).
Molecules 19 05278 g002
Table
Table 1. Calculated rate constants for the switching of C to S (kC→S) and for the switching of S to C (kS→C) at different temperatures, and the equilibrium constant K that represents the ratio of S/C at equilibrium.
Table 1. Calculated rate constants for the switching of C to S (kC→S) and for the switching of S to C (kS→C) at different temperatures, and the equilibrium constant K that represents the ratio of S/C at equilibrium.
T (°C)kC→S (s−1) akS→C (s−1) b,cK b
252.8 × 10−63.7 × 10−77.6
32.56.0 × 10−61.0 × 10−65.8
401.5 × 10−52.8 × 10−65.3
47.53.2 × 10−56.8 × 10−64.7
a Estimated error 5%; b Estimated error 15%; c Calculated from kS→C = kC→S/K.
The switching from C to S was monitored at four different temperatures (Figure 3a) from which, with the help of van’t Hoff and Eyring plots, the entropic (ΔS) and enthalpic (ΔH) contributions to the activation energy (ΔG≠) and the free energy of binding (ΔG°) could be determined. The resulting energy diagram with all these parameters is presented in Figure 3b. The switching process is unfavorable both in entropy and in enthalpy, but the majority of the free energy of activation (ΔG≠) is enthalpic in origin (the proposed mechanism will be presented later).
The obtained parameters ΔS° and ΔH° (Figure 3b) revealed that the formation of the trans-linked isomer S is enthalpically more favorable than the cis-linked isomer C, whereas the latter is entropically more likely to form. The value of ΔH° suggests that S experiences more stabilizing intramolecular interactions than C. These are presumably π-π interactions between the phenyl groups of the handles and the porphyrin plane, and additional van der Waals interactions. The entropic parameters suggest that C is more disordered than S, which could be the result of a restricted motion of the handles in S as a result of the intramolecular binding interactions (entropy-enthalpy compensation [45]). Another possibility is that S needs to organize more solvent molecules in a defined shell than C, which would result in the release of solvent to the bulk upon switching from S to C, thereby accounting for the entropic gain. The observation that C dissolves significantly better in the used solvent mixture than S could validate this hypothesis, although solubility depends on more factors.
Molecules 19 05278 g003 550
Figure 3. (a) Kinetics of switching from C to S at different temperatures in CDCl3/CD3CN 1:1 (v/v), monitored by 1H-NMR. (b) Energy diagram of the switching process with the entropic and enthalpic parameters (all in kJ/mol).
Figure 3. (a) Kinetics of switching from C to S at different temperatures in CDCl3/CD3CN 1:1 (v/v), monitored by 1H-NMR. (b) Energy diagram of the switching process with the entropic and enthalpic parameters (all in kJ/mol).
Molecules 19 05278 g003

2.4. Binding of Viologen Derivatives

The binding of viologen derivatives V1, V2, and V3 (Figure 4) to isomers C and S was investigated. As a result of the high kinetic stabilities of C and S, no detectable isomerization was observed in the first few hours after their separation, which allowed the study of the binding properties of the individual isomers. A 1H-NMR titration between C and V1 revealed that V1 binds strongly to this receptor in a face-to-face geometry with respect to the porphyrin [46]. The addition of increasing amounts of V1 to C resulted in large downfield complexation induced shift (CIS) values of the crown ether proton resonances (H-3 to H-6), which indicates that their position in the proximity of the porphyrin is replaced by V1 (Table 2). The pyrrole NH resonances of C shifted dramatically upfield upon complex formation, indicating their shielding by the aromatic rings of V1. Also the signals of V1 displayed large upfield shifts compared to their original positions, confirming their position in the proximity of the shielding porphyrin ring current. The addition of one equivalent of V1 resulted in the full binding to C, stressing the strong affinity between the components. To derive an accurate value for the association constant (KCV1), the binding of V1 to C was investigated at lower concentrations ([C] ≈ 10−6 M) with the help of a fluorescence titration. The addition of increasing amounts of V1 to a solution of C resulted in the quenching of the porphyrin fluorescence of the receptor. The obtained binding curve could be fitted with a 1:1 binding isotherm and the association constant was calculated to be KCV1 = 3 × 105 M−1 (Table 3).
Molecules 19 05278 g004 550
Figure 4. Structure of viologens V1 and V2 and pyridinium compound V3.
Figure 4. Structure of viologens V1 and V2 and pyridinium compound V3.
Molecules 19 05278 g004
Table
Table 2. Selected calculated CIS values (ppm) of receptor proton signals upon binding of viologens to S and C. a
Table 2. Selected calculated CIS values (ppm) of receptor proton signals upon binding of viologens to S and C. a
Proton bCS
V1V2V3 dV1V2 eV3 d
H-10.000.010.01−0.28−0.06−0.28
H-2−0.03−0.10−0.03−0.13−0.08−0.06
H-3 to H-5 c0.420.43f0.47f0.50
H-6a0.510.64f0.25f0.21
H-6b0.470.29f0.21f0.17
N-H−1.04−0.98−0.51−1.12−0.33−0.85
a Calculated from 1H-NMR experiments (400 MHz, 298 K, CDCl3/CD3CN 1:1 (v/v)); b See Scheme 1 for proton numbering; c Average shifts of the series of protons; d Concentration V3: 1 × 10−2 M; e Concentration V2: 3.3 × 10−3 M; f Resonances were obscured.
Table
Table 3. Association constants (Ka) and binding free energies (ΔG°) at 298 K and the enthalpic (ΔH°) and entropic (ΔS°) contribution to the binding free energy between isomers C and S and viologen guests.
Table 3. Association constants (Ka) and binding free energies (ΔG°) at 298 K and the enthalpic (ΔH°) and entropic (ΔS°) contribution to the binding free energy between isomers C and S and viologen guests.
Receptor isomerGuestKac(M−1)Δ G°(kJ/mol)Δ H° d(kJ/mol)Δ S° eJ/molK
SV1 ( KSV)1.3 × 104a,b−23.6−31.3−25.9
V1 ( KVSV)6.0 × 102a−15.8
CV13.0 × 105b−31.2−30.1+3.7
V23.5 × 103a−20.2
a Determined in CDCl3/CD3CN 1:1 (v/v) by 1H-NMR titrations; b Determined In CHCl3/CH3CN 1: (v/v) by fluorescence titrations; c Estimated error 30%; d Estimated error 10 kJ/mol; e Estimated error 10 J/molK.
Molecular modeling revealed that V1 preferably accommodates its positive charges in between the two “handle” crown ether rings of C. The complex adopts a so called suit[2]ane [47] geometry in which the positive charges are wrapped inside the crown ether sleeves of the suit-shaped receptor C (see Figure 5a). Since it is impossible to directly derive the exact geometry of the complex with the help of NMR techniques, and attempts to obtain an X-ray structure of the complex were unsuccessful, it was decided to compare the binding between C and V1 with that between C and V2. V2 cannot adopt the proposed suit[2]ane geometry as a result of the presence of 3,5-di-tert-butylphenyl blocking groups, which can impossibly slip through the crown ether rings of C. A 1H-NMR titration between C and V2 indicated that V2 adopts a different binding geometry with C than V1. Although V2 also binds in a face-to-face orientation with respect to porphyrin plane of C, as can be concluded from the observed upfield shift of the pyrrole NH proton resonances of the receptor (Table 2), the CIS values for all the other proton resonances are significantly different for the complex between C and V2 when compared to the complex between C and V1. Moreover, the association constant for the binding of V2 to C is almost two orders of magnitude lower than that for the binding of V1 to C (Table 3). These combined results strongly suggest that V1 indeed binds to C in the proposed suit[2]ane geometry, whereas V2 adopts a geometry as indicated in Figure 5b.
Molecules 19 05278 g005 550
Figure 5. Molecular models, based on the binding studies, of the 1:1 complexes between (a) C and V1, (b) C and V2 (blocking groups are not shown for clarity), (c) S and V1 and (d) the 1:2 complex between S and V1.
Figure 5. Molecular models, based on the binding studies, of the 1:1 complexes between (a) C and V1, (b) C and V2 (blocking groups are not shown for clarity), (c) S and V1 and (d) the 1:2 complex between S and V1.
Molecules 19 05278 g005
In addition to the binding to C, the binding of V1 to trans-linked S was investigated. A 1H-NMR titration revealed complex formation between V1 and S, which was expressed in large CIS values for the proton resonances of V1 and S. As observed for the binding of V1 with C, the pyrrole NH proton resonances and aromatic viologen signals shifted upfield, whereas the crown ether proton resonances shifted downfield (Table 2), which suggests a binding geometry in which the porphyrin ring of S and the aromatic rings V1 adopt a face-to-face orientation (Figure 5c). The experimentally obtained binding curve could however not be fitted with a 1:1 binding isotherm, which strongly points in the direction of 1:2 complex formation between S and V1. This was moreover indicated by the CIS value of the pyrrole NH proton signals of S (Table 2). These signals shifted significantly further upfield upon complexation of V1 than in the complex between V1 and C (and other known face-to-face viologen-porphyrin complexes known in literature [41,48,49]), which indicates that this is the result of the presence of two viologen molecules that are sandwiching the porphyrin (Figure 5d). Data analysis of the binding curves with a 1:2 host-guest binding isotherm gave a satisfying fit with association constants of 1.3 × 104 M−1 and 6 × 102 M−1 for the binding of the first (KSV) and second (KVSV) molecule of V1 to S, respectively. Considering the statistical factor of 4 for the difference in binding of the first and the second identical guest molecule to a bivalent receptor, there is a negative cooperative effect for the binding of the second molecule of V1 to S with an α-value of 0.18. This is most probably caused by the repulsive interactions between the positive charges of the two viologen derivatives [50].
Because the guest-induced switching between the conformers, which will be presented in the following sections, is performed at elevated temperatures, the effect of temperature on the binding constants of V1 to S and C, respectively, was studied with the help of fluorescence titrations. Although V1 was shown to form 1:2 host-guest complexes with S at 1H-NMR concentrations (10−3 M), at the used experimental concentrations of the fluorescence titrations (10−6 M) 1:2 complex formation was so marginal that it could be ignored, and the obtained fluorescence titration curves could therefore be fitted with the use of simple 1:1 binding isotherms. This was emphasized by both the good fits and the calculated value of the association constant that were obtained from the fluorescence titration for the 1:1 complex between V1 and S, which was in very good agreement with the value of KSV obtained from the 1H-NMR titration experiment at the same temperature [51]. With the use of Van het Hoff plots, the enthalpic (ΔH°) and entropic (ΔS°) contributions to the total free binding energy (ΔG°) of V1 with S and C, respectively, could be determined. Quite surprisingly, the calculated parameters revealed that the differences in binding strength between V1 and C and V1 and S, respectively, are mainly entropic in origin (Table 3). Similar values were obtained for the binding enthalpy (ΔH°). Complex formation between C and V1 is slightly favorable in entropy, whereas complex formation between S and V1 is unfavorable in entropy.
Intuitively, two good reasons can be envisaged why the binding of V1 to C should be enthalpically more favorable than the binding of V1 to S. The first reason is that isomer C can provide more stabilizing interactions to V1 than isomer S as a result of the presence of two crown ether handles, which can both interact with the viologen guest, on the same side of the porphyrin plane. The second reason is that within isomer S more intramolecular interactions are present than within C, which have to be overcome in order to accommodate V1 (as suggested by the value of ΔH° for the switching process as presented above). The fact that no enthalpic difference is observed between the two binding processes, and that the difference in binding is mainly entropic in origin, therefore suggests that the binding of viologen derivatives to both isomers depends to a crucial extent on the desolvation of the viologen derivatives upon complex formation. Isomer C can fully accommodate the positive charges of the viologen, thereby perfectly shielding it from the solvent (Figure 5a). In contrast, isomer S is only capable of shielding one of the positive charges of the viologen from the solvent (Figure 5c). As a result, the binding of V1 to C is accompanied by the release of more solvent molecules to the bulk than the binding of V1 to S, which accounts for the observed difference in binding entropy.

2.5. Guest-Induced Switching: Thermodynamics

As a result of the higher affinity of V1 for C than for S (∆∆G° = 7.6 kJ/mol), it would be expected that in the presence of the guest the equilibrium should be switched further in the direction of the thermodynamically less favorable isomer C. Because S is 5 kJ/mol more stable than C (Figure 4b), it could theoretically result in an equilibrium situation which has its free energy shifted maximally 2.6 kJ/mol in the direction of C, and which would be translated into a ratio of approximately 74% C and 26% S at equilibrium, or [S]tot-eq/[C]tot-eq = 0.36. A first isomerization experiment, in which a mixture of S and V1 was annealed at 80 °C in toluene/acetonitrile 1:1 (v/v) for 12 h, indeed revealed that the conformational equilibrium had shifted in the direction of C. After workup and purification of the reaction mixture, the different isomers were isolated in a ratio of approximately C:S = 2:1. This ratio is strikingly different from the ratio obtained after annealing isomer S under the same experimental conditions but in the absence of V1, which amounted to C:S ≈ 1:5.
In order to gain more detailed information about the guest-induced switching, it was decided to follow the switching from S to C in the presence of V1 with the help of 1H-NMR spectroscopy. The 1H-NMR spectra of a mixture of S (1 mM) and V1 (1.3 mM) in CDCl3/CD3CN 1:1 (v/v) at 37.5 °C revealed that in time isomer C was formed at the expense of isomer S (Figure 6), resulting in a final equilibrium ratio of [S]tot-eq/[C]tot-eq = 0.56 (64% C and 36% S). This ratio is different from the ratio (0.36) mentioned above because of the different solvent mixture and the different temperature.
Molecules 19 05278 g006 550
Figure 6. Series of partial 400 MHz 1H-NMR spectra recorded over time, revealing the decrease in population of isomer S at the expense of the population of isomer C in the presence of 1.3 equiv. of V1 at 37.5 °C in CDCl3/CD3CN 1:1 (v/v).
Figure 6. Series of partial 400 MHz 1H-NMR spectra recorded over time, revealing the decrease in population of isomer S at the expense of the population of isomer C in the presence of 1.3 equiv. of V1 at 37.5 °C in CDCl3/CD3CN 1:1 (v/v).
Molecules 19 05278 g006
To further explore the switching effect of V1, the isomerization from S to C in solutions containing varying concentrations of this guest was monitored by 1H-NMR spectroscopy. The measurements revealed that there is an optimal concentration of V1 in which the equilibrium ratio ([C]tot/{[C]tot + [S]tot}) is shifted furthest in the direction of [C]tot (Figure 7a and Table 4), after which increasing concentrations of V1 resulted slowly in the shifting back of the conformational ratio in the direction of [S]tot. This observation is attributed to the possibility of also forming the 1:2 complex between S and V1, as presented in Figure 8. At relatively low concentrations of V1, the equilibrium will shift towards the 1:1 complex between V1 and C (since KCV > KSV) and thus in the direction of [C]tot. At further increasing concentrations of V1, however, the formation of the 1:2 complex between S and V1 will become more favorable, which results in a shifting back of the equilibrium situation towards [S]tot. This behavior follows directly from Equation (1), which presents the equilibrium constant (Kswitch) as a function of free V1 in solution ([V]) and all the individual equilibrium constants:
Molecules 19 05278 i001
In Equation (1), KS/C is the equilibrium constant between S and C in the absence of viologen guests, KSV and KCV are the association constants of V to S and C, respectively, for the formation of the 1:1 complexes, and KVSV is the association constant for the formation of the 1:2 complex between S and V. The concentration of free V is obviously directly related to the concentration of isomers C and S in solution, but it is clear from Equation (1) that there will exist a concentration of V in which Kswitch has a minimum value and thus that [C]tot will be maximal. The value for Kswitch as a function of different equilibrium constants and concentrations of V1 could be determined numerically with the use of Mathematica®. Although the experimental data did not exactly match the theoretical calculations on the basis of all the experimentally derived individual equilibrium constants, as can be seen in Figure 7a (which is not surprising, since four equilibrium constants are involved, some of which have errors of up to 30% and KVSV had to be estimated), the trend in switching is clearly as would be expected on the basis of the binding model in Figure 8. Moreover, the data could be fitted with the assumed binding model and the calculated equilibrium constants as obtained by the fit did not deviate significantly from the experimentally derived values for the individual equilibrium constant (see Figure 7a).
Molecules 19 05278 g007 550
Figure 7. (a) Equilibrium ratios ([C]tot/([S]tot + [C]tot}) at 37.5 °C ( Molecules 19 05278 i002) and 47.5 °C ( Molecules 19 05278 i003) plotted against the concentration of V1 present in solution and the expected equilibrium ratios ([C]tot/([S]tot + [C]tot}) based on the experimentally derived individual equilibrium constants (thin lines) and the bests fits (thicker lines matching the data points) of the experimental data (37.5 °C: KS/C = 5.5, KSV = 1.5 × 104 M−1, KVSV = 2.0 × 102 M−1, KCV = 1.8 × 105 M−1. 47.5 °C: KS/C = 4.7, KSV = 7.0 × 103 M−1, KVSV = 70 M−1, KCV = 9.5 × 104 M−1). (b) Observed initial rates (kS→C-obs) for the switching of S to C in solutions with different concentrations of V1 at 37.5 °C. The framework represents the theoretical rates based on different values of the cooperativity factor (cf), assuming equilibrium constants KSV = 1.5 × 104 M−1 and KVSV = 2.0 × 102 M−1.
Figure 7. (a) Equilibrium ratios ([C]tot/([S]tot + [C]tot}) at 37.5 °C ( Molecules 19 05278 i002) and 47.5 °C ( Molecules 19 05278 i003) plotted against the concentration of V1 present in solution and the expected equilibrium ratios ([C]tot/([S]tot + [C]tot}) based on the experimentally derived individual equilibrium constants (thin lines) and the bests fits (thicker lines matching the data points) of the experimental data (37.5 °C: KS/C = 5.5, KSV = 1.5 × 104 M−1, KVSV = 2.0 × 102 M−1, KCV = 1.8 × 105 M−1. 47.5 °C: KS/C = 4.7, KSV = 7.0 × 103 M−1, KVSV = 70 M−1, KCV = 9.5 × 104 M−1). (b) Observed initial rates (kS→C-obs) for the switching of S to C in solutions with different concentrations of V1 at 37.5 °C. The framework represents the theoretical rates based on different values of the cooperativity factor (cf), assuming equilibrium constants KSV = 1.5 × 104 M−1 and KVSV = 2.0 × 102 M−1.
Molecules 19 05278 g007
Table
Table 4. Calculated rate constants (kS→C-obs) and equilibrium constants (Kswitch) for the switching of S to C in solutions with different concentrations of viologen guests V1−V3. a
Table 4. Calculated rate constants (kS→C-obs) and equilibrium constants (Kswitch) for the switching of S to C in solutions with different concentrations of viologen guests V1−V3. a
GuestConc (mM)kS→C-obsb,d (s−1)Kswitchc,e
No01.8 × 10−65.5
V10.52.3 × 10−61.0
V11.33.0 × 10−60.6
V12.62.7 × 10−60.6
V13.12.6 × 10−60.7
V16.51.9 × 10−61.0
V23.32.4 × 10−60.9
V3201.1 × 10−610.0
a Determined by 1H-NMR experiments in CDCl3/CD3CN 1:1 (v/v) at 37.5 °C; b Calculated from the initial 25% of the switching curves; c Calculated from the ratio [S]tot/[C]tot at equilibrium; d Estimated error 20%; e Estimated error 15%.
Molecules 19 05278 g008 550
Figure 8. Binding scheme of the isomerization between S and C in the presence of V1.
Figure 8. Binding scheme of the isomerization between S and C in the presence of V1.
Molecules 19 05278 g008
In addition to experiments in which switching was induced by V1, also experiments were carried out in which switching was triggered by the doubly blocked guest V2 and the guest V3 (1-methyl-4-phenylpyridinium hexafluorophosphate). As can be seen in Figure 9, also V2 is capable of switching the equilibrium in the direction of C, which indicates that this guest has a higher affinity for C than for S. This binding process was further confirmed by the gradually upfield shifting aromatic resonances of the guest in time upon switching from S to C in the 1H-NMR spectra. Although the binding of V2 to S was not studied in detail, it is obvious that C can provide more stabilizing interactions (or cause more solvent shielding upon complex formation) to V2 than S. The switching experiment in the presence of V3 (20 equiv.) revealed that this guest is not capable of switching the equilibrium in the direction of [C]tot. Instead, it causes the opposite effect and the equilibrium is shifted more in the direction of [S]tot (Figure 9). This observation suggests that S has a higher affinity for V3 than C, which is more or less in line with expectation since only one handle is needed for the accommodation of the single positive charge of V3 [52].
Molecules 19 05278 g009 550
Figure 9. Kinetics of the switching of S (1 × 10−3 M) to C in the absence of guest ( Molecules 19 05278 i004) and in the presence of 1.3 equivalents of V1 ( Molecules 19 05278 i002), 3.3 equivalents of V2 ( Molecules 19 05278 i005) and 20 equivalents of V3 ( Molecules 19 05278 i006). The line represents the calculated curve for the switching in the presence of 1.3 equivalents of V1 assuming no induced switching effect.
Figure 9. Kinetics of the switching of S (1 × 10−3 M) to C in the absence of guest ( Molecules 19 05278 i004) and in the presence of 1.3 equivalents of V1 ( Molecules 19 05278 i002), 3.3 equivalents of V2 ( Molecules 19 05278 i005) and 20 equivalents of V3 ( Molecules 19 05278 i006). The line represents the calculated curve for the switching in the presence of 1.3 equivalents of V1 assuming no induced switching effect.
Molecules 19 05278 g009

2.6. Guest-Induced Switching: Kinetics

In addition to the thermodynamics we also investigated the kinetics of the guest-induced switching. The observed initial rates (kS→C-obs) in solutions with different concentrations of V1 at 37 °C were calculated from the initial 25% of the switching curves, as obtained by 1H-NMR spectroscopy. The data, which are presented in Figure 7b and Table 4, reveal that the observed initial rates increase upon increasing concentrations of V1, and reach a maximum value after which they decrease again. This decrease is fully in line with expectation, since increased concentrations of V1 shift the initial equilibrium further in the direction of the 1:2 host-guest complex VSV (Figure 8) in which both handles are restricted from rotation. The initial increase in rate in solutions with lower concentrations of V1, on the other hand, is surprising and suggests that the switching is enhanced by the presence of V1. Statistically, it can be expected that the switching rate from S to C in the presence of V1 (kSV→CV, see Figure 9) is a factor 2 lower than in the absence of V1 (kS→C) as a result of the restricted rotation of one of the handles of S upon complex formation with V1. If a viologen-induced rate enhancement is not taken into account, the observed switching rates (kS→C-obs) should therefore decrease upon complex formation between V1 and S, and drop even further upon a further increase in concentration of V1, as a result of 1:2 host-guest complex formation. In order to be able to fit the experimental data, a rate enhancement factor (cf) has to be included into the model. The initial rate (kS→C-obs) should evolve as a function of [S], [SV] and [VSV] according to Equation (2), in which kSV→CV is defined according to Equation (3) in which both the statistical factor of 0.5 and the rate enhancement factor is taken into account:
kS→C-obs = kS→C·[S]/[S]tot + kSV→CV·[SV]/[S]tot
kSV→CV = cf·0.5·kS→C
kSV→CV = cf·0.5·kS→C·KSV/KCV
Since the individual constants kS→C, KSV and KVSV were determined separately (see above), the magnitude of the factor cf could be calculated. To this end, the expected overall initial rate constants were calculated with the help of Mathematica® as a function of the magnitude of cf and the concentration of V1 (which determines the ratios of [S], [SV] and [VSV]). The calculated rates as a function of V1 are presented as the framework in Figure 7b, and from this framework it can be concluded that the magnitude of cf is approximately 4, hence the switching rate is enhanced in the presence of V1 by a factor of 4. In order to stress the acceleration of the switching process in the presence of V1, the expected kinetic curve of switching from S to C under the same conditions, assuming cf = 1, is presented in Figure 9. In addition to V1, also V2 clearly accelerates the switching process, as can be observed in Figure 9 and Table 4. The observed rate (kS→C-obs) in the presence of V3, on the other hand, is lower than kS→C (Table 4), which indicates that the switching rate is not enhanced by V3.

2.7. Mechanism

The magnitudes of the rate constants and the enthalpic and entropic contributions to the transition state energy for the switching process between the isomers C and S are all very similar to the values observed for atropisomerization of ortho-meso-phenyl-substituted porphyrins, involving rotations around one single bond [53,54,55,56,57,58,59]. This suggests that the mechanism of isomerization between C and S is not significantly different from other porphyrin atropisomerization processes. For this reason, the switching between S and C most probably does not occur not via simultaneous but via consecutive rotations around the two porphyrin meso-phenyl rings. As a result, the switching consists of two steps that have similar activation barriers, with in between them a local energy minimum in which the handle is halfway the switching process (T in Figure 10). The energy level of T is unfavorable compared to both the energy levels of S and C making that it cannot be observed experimentally. The presence of V1 in the switching process is expected to have a significant influence on the relative energy levels. The same interactions that cause that the complex CV is energetically more favorable than the complex SV (Figure 10) will influence the transition state of the switching process. Transition state intermediate complex TV will experience additional stabilizing interactions compared to T as a result of the fact that half the handle is switched to the side of the viologen (hence [T]/[S] > [TV]/[SV]). Also the rotation around the second porphyrin meso-phenyl ring in the switching process from T to C is energetically more favorable as a result of these interactions. The viologen guest thus lowers the barriers associated with the switching process and effectively pulls the handle through to the other side of the porphyrin. Note that these same interactions should also cause a similar rate enhancement while switching back from C to S, in line with the principle of microscopic reversibility. The observation that both V1 and V2 (which binds in 90 degrees rotated geometries with respect to the porphyrin) accelerate the switching process is in line with this mechanism, since independent of the geometry of the eventual complexes, both V1 and V2 can exert these stabilizing interactions in the transition state. V3 most probably accommodates its positive charge inside one crown ether handle and is consequently not capable of stabilizing the transition state involving the switching of the other handle, which accounts for the apparent absence of rate enhancement in the presence of V3.
Molecules 19 05278 g010 550
Figure 10. Proposed energy landscape of the switching between C and S in absence and in the presence of V1.
Figure 10. Proposed energy landscape of the switching between C and S in absence and in the presence of V1.
Molecules 19 05278 g010

3. Experimental

3.1. Materials and Methods

All solvents and chemicals were used as received. K2CO3 was dried in an oven (150 °C). Chloroform and acetonitrile used in fluorescence titration experiments were distilled from CaCl2. Preparative TLC was performed on Merck (Darmstadt, Germany) silica glass plates (TLC Silica gel 60 F254). Fluorescence experiments were performed on a Perkin-Elmer LS50B luminescent spectrometer (Waltham, MA, USA) equipped with a thermostatted cuvette holder. UV-Vis spectra were recorded on a Cary 100 Conc UV-Vis spectrometer (Varian, Middelburg, The Netherlands). Maldi-TOF mass spectrometry was performed on a Bruker Biflex III spectrometer (Billerica, MA, USA). NMR spectra were taken on a Varian (Palo Alto, CA, USA) Inova 400 (400 MHz, 1H and 2D spectra) or on a Bruker (Billerica, MA, USA) DMX300 (75 MHz, 13C spectra) and calibrated to an internal standard of tetramethylsilane.The synthesis of ditosylate 1 was reported elsewhere [41]. The syntheses of 5,10,15,20-tetrakis(meso-o-hydroxyphenyl)porphyrin 2 [42], V1 [41] and V2 [60] are also described in the literature.

3.2. Syntheses

3.2.1. “Basket Handle” Isomers X, S and C

A suspension of 1 (0.90 g, 1.51 mmol), 5,10,15,20-tetrakis(meso-p-hydroxyphenyl)-porphyrin 2 (0.50 g, 0.74 mmol) and K2CO3 (1 g, 7.2 mmol) in DMF (250 mL) was reacted for 16 h under an argon atmosphere at 110 °C. After filtration of the salts and evaporation of the solvents the product was purified by column chromatography (3% MeOH in CHCl3 (v/v)) yielding 450 mg (52%) of a mixture of isomers X, S and C. The three isomers could be separated by preparative TLC (5:5:1 toluene/ethyl acetate/acetonitrile (v/v/v)) to give the products in a ratio of X:S:C = 4:8:1. (adjacent-trans-linked S could also be selectively crystallized out of a mixture of 5:1 acetonitrile/chloroform (v/v) containing isomers C and S) The separate products were dissolved in a minimal amount of CHCl3 and to this solution n-pentane was added. This resulted in precipitates, which were collected by centrifugation and dried under vacuum at low temperatures yielding the different isomers X, S and C as purple solids. In order to prevent isomerization between C and S, both speed and low temperatures are of essential importance in the separation process.
Data for cross-trans-linked “basket handle” porphyrin isomer X: 1H-NMR (CDCl3 400 MHz) δ 8.71 (s, 8H), 7.75 (d, 4H, J = 7.2 Hz), 7.69 (t, 4H, J = 7.9 Hz), 7.22 (d, 4H, J = 8.3 Hz), 7.12 (t, 4H, J = 7.4 Hz), 6.83 (m, 4H), 6.60 (m, 4H), 4.00 (M, 8H), 3.00 (M, 8H), 2.25 (t, 8H, J = 4.5 Hz), 1.59 (t, 8H, J = 4.6 Hz), −2.72 (s, 2H) ppm. 13C-NMR (CDCl3 75 MHz) δ 158.68, 149.16, 135.02, 130.91, 129.69, 122.30, 119.60, 117.65, 115.65, 111.04, 69.65, 69.21, 68.63, 68.42 ppm. MALDI TOF m/z = 1180 (M + H+). UV-Vis (CHCl3) λ/nm (log(ε·M−1cm−1)) 418.5 (5.6), 513.0 (4.3), 546.5 (3.8), 589.0 (3.8), 643.5 (3.5).
Data for adjacent-trans-linked “basket handle” porphyrin isomer S: 1H-NMR (CDCl3 400 MHz) δ 8.69 (s, 4H), 8.68 (s, 4H), 8.00 (dd, 4H, J = 1.7 Hz, J = 7.4 Hz), 7.75 (ddd, 4H, J = 1.7 Hz, J = 7.6 Hz, J = 8.3 Hz), 7.39 (dt, 4H, J = 1.0 Hz, J = 7.5 Hz), 7.28 (dd, 4H, J = 0.8 Hz, J = 8.4 Hz), 6.27 (dd, 4H, J = 3.5 Hz, J = 6.0 Hz), 5.70 (dd, 4H, J = 3.6 Hz, J = 5.9 Hz), 3.94 (m, 8H), 3.08 (m, 4H), 2.88 (m, 4H), 2.27 (m, 4H), 1.94 (t, 8H, J = 3.9 Hz), 1.51 (m, 4H), −2.88 (s, 2H) ppm. 13C-NMR (CDCl3 75 MHz) δ 158.82, 147.91, 134.91, 131.60, 129.79, 120.89, 119.85, 115.41, 114.67, 112.43, 69.41, 69.01, 68.60, 68.04 ppm. MALDI TOF m/z = 1180 (M + H+). UV-Vis (CHCl3) λ/nm (log(ε·M−1cm−1)) 419.5 (5.6), 513.5 (4.3), 547.0 (3.9), 589.0 (3.9), 645.0 (3.5).
Data for adjacent-cis-linked “basket handle” porphyrin isomer C: 1H-NMR (CDCl3 400 MHz) δ 8.74 (s, 4H), 8.74 (s, 4H), 7.95 (dd, 4H, J = 1.7 Hz, J = 7.4 Hz), 7.74 (ddd, 4H, J = 1.8 Hz, J = 7.5 Hz, J = 8.3 Hz), 7.37 (dd, 4H, J = 1.0 Hz, J = 7.1 Hz), 7.34 (m, 4H), 6.36 (dd, 4H, J = 3.6 Hz, J = 6.0 Hz), 6.26 (dd, 4H, J = 3.6 Hz, J = 6.0 Hz), 4.11 (td, 4H, J = 5.6 Hz, J = 11.1 Hz), 4.00 (m, 4H), 3.33 (m, 4H), 3.22 (m, 8H), 2.96 (m, 8H), −2.75 (s, 2H) ppm. 13C-NMR (CDCl3 75 MHz) δ 158.65, 148.58, 136.03, 131.63, 129.72, 121.22, 119.88, 115.65, 114.89, 112.90, 69.54, 69.28, 69.09, 68.80 ppm. MALDI TOF m/z = 1180 (M + H+). UV-Vis (CHCl3) λ/nm (log(ε·M−1cm−1)) 420.0 (5.6), 514.5 (4.3), 550.0 (3.8), 591.0 (3.8), 646.5 (3.4).

3.2.2. 1-Methyl-4-phenylpyridinium hexafluorophosphate (V3)

4-Phenylpyridine (200 mg, 1.2 mmol) was stirred with an excess of methyl iodide (0.5 mL) in acetonitrile (5 mL) for 48 h. Diethyl ether (5 mL) was added, the resulting precipitate was removed by filtration, washed with diethyl ether, and dried under vacuum. The product was dissolved in a minimal amount of water, and this solution was then added to a saturated aqueous NH4PF6 solution to yield, after filtration, washing with water and drying under vacuum, 100 mg (25%) of V3 as a white solid. 1H-NMR (CDCl3/CD3CN 1:1 (v/v), 400 MHz): δ 8.61 (d, 2H, J = 6.3 Hz), 8.22 (d, 2H, J = 6.3 Hz), 7.9 (d, 2H, J = 7.3 Hz), 7.67–7.62 (m, 3H), 4.32 (s, 3H) ppm. 13C-NMR (CDCl3/CD3CN 1:1 (v/v), 75 MHz): δ 155.92, 144.61, 131.94, 129.41, 127.52, 124.47, 116.54, 47.16 ppm.

3.3. X-ray Analysis of S

A single crystal was mounted in air on a glass fibre. Intensity data were collected at −65 °C. A Nonius KappaCCD single-crystal diffractometer (manufacturer, city, country) was used (φ and ω scan mode) using graphite monochromated Mo-Kα radiation. Unit cell dimensions were determined from the angular setting of 227 reflections. Intensity data were corrected for Lorentz and polarization effects. SADABS multiscan correction [61] was applied. The structure was solved by the program CRUNCH [62] and was refined with standard methods using SHELXL97 [63]) with anisotropic parameters for the non-hydrogen atoms. All hydrogens were placed at calculated positions and were refined riding on the parent atoms. A structure determination summary is given in Table 5. CCDC 988037 contains the supplementary crystallographic data for this paper [64].

3.4. Determination of Association Constants

The association constants were determined by means of fluorescence- and 1H-NMR titrations. For the 1:2 binding of S to V1 the experimental error was quite large because of uncertainties involved with determining two association constants from one single binding experiment. The fluorescence titrations giving association constants KSV1 and KCV1 were performed once, and although very good fits were obtained for the individual experiments, the experimental error was chosen on the conservative side (30%). Experimental errors evolving from weighing small quantities of receptor and potential atropisomerization during the experiment could not be fully excluded (all effort was taken to prevent this phenomenon: both S and C were purified directly before the binding studies, analyzed using 1H-NMR, and kept cold for as long as possible before the binding experiment to prevent the switching). For individual titration data, see below.
Table
Table 5. Crystallographic data for isomer S.
Table 5. Crystallographic data for isomer S.
Crystal PropertyValue
Identification codeCLIP10
Crystal colourdark purple
Crystal shaperough thick platelet
Crystal size0.21 × 0.20 × 0.05 mm
Empirical formulaC72 H66 N4 O12
Formula weight1179.29
Temperature208(2) K
Radiation/WavelengthMoKα (graphite monochromated)/0.71073 Å
Crystal system, space groupMonoclinic, P21/a
Unit cell dimensionsa, alp = 12.9808(4) Å, 90°
44169 reflectionsb, bet = 14.6770(9) Å, 105.642(4)°
1.900 < theta < 25.000c, gam = 16.2856(12) Å, 90°
Volume2987.8(3) Å3
Z, Calculated density2, 1.311 Mg/m3
Absorption coefficient0.090 mm−1
Diffractometer/scanNonius KappaCCD with area detector φ and ω scan
F(000)1244
Theta range for data collection1.90 to 27.50°.
Index ranges−16 <= h<= 16, −18 <= k <= 18, −21 <= l <= 21
Reflections collected/unique 50597/6846 [R(int) = 0.0684]
Reflections observed4082 ([Io > 2σ(Io)])
Completeness to 2theta = 25.0095.7%
Absorption correctionSADABS multiscan correction (Sheldrick,1996)
Refinement methodFull-matrix least-squares on F2
ComputingSHELXL-97 (Sheldrick, 1997)
Data/restraints/parameters6846/0/398
Goodness-of-fit on F^21.084
SHELXL-97 weight parameters0.033600 2.925100
Final R indices [I > 2sigma(I)]R1 = 0.0788, wR2 = 0.1286
R indices (all data)R1 = 0.1434, wR2 = 0.1485
Largest diff. peak and hole 0.871 and −0.257 e.Å−3
The association constants for the 1:1 complex formation between the different isomers and viologen derivatives were determined according to standard fitting procedures. The association constants for the 1:2 complex formation between S and V1 in the 1H-NMR titration experiment were fitted with the use of Mathematica®, in which the association constant KSV was varied and the fit provided the value of KVSV. In this paper the values for KSV and KVSV of the optimized fit are given. For a detailed description of the procedure we refer to the Supplementary Material.
The assumption that at lower concentrations the binding of V1 to S can be fitted with the use of a 1:1 binding isotherm can also be shown analytically. In a titration of S with a viologen V in which 1:2 complex formation is allowed both the 1:1 complex SV and the 1:2 complex VSV can form. The overall binding process in the titration is therefore: S + 2V ↔ SV + 18VSV. The association constants for the 1:1 (KSV) and the 1:2 complex formation (KVSV) are presented in Equations (5) and (6).
Molecules 19 05278 i007
Molecules 19 05278 i008
From the apparent association constant, which is given in Equation (7), it becomes clear that this constant, which describes the equilibrium of the combined 1:1 and 1:2 complexes, changes upon increasing the concentration of V. There is, however, a certain concentration regime in which the deviations between Equations (5) and (7) are very marginal. As long as KVSV·[V] is small, the overall binding process does not deviate from a 1:1 binding process. At the experimental concentrations, the maximum concentration of V1 ([V]o) was never higher than 1 × 10−4 M and the concentration of S ([S]o) was 1 × 10−6 M. Because of this excess of V1 it can be safely stated that [V]o ≈ [V]. Assuming an association constant KVSV of 600 M−1 as derived from the 1H-NMR titration, it becomes clear that the apparent association constant deviates only 6% from the 1:1 binding behavior at the final point of the titration (KVSV·[V] = 0.06), whereas in the initial part of the titration, in which lower concentrations of V are present, this deviation will be even smaller. Since this error is by no means larger than the experimental error in the chosen concentration regime of the titration experiment, accurate fits can be obtained with the help of 1:1 binding isotherms.
Molecules 19 05278 i009

4. Conclusions

We have shown that the presence of viologen guests has a large influence on the thermodynamics and kinetics of the atropisomerization reaction between an adjacent-cis-linked and an adjacent-trans-linked “basket handle” porphyrin. The thermodynamic product of the guest-induced switching process strongly depends on the relative affinities of the individual isomers for the different viologen guests. In all cases, the switching experiments were in very good agreement with theoretical predictions based on the individual equilibrium constants. The kinetic studies of the switching process revealed that the presence of viologen derivatives actually enhances the rate of the switching process. It is suggested that this enhancement is caused by favorable interactions between the positively charged guest and the crown ethers of the receptor in the process of switching, which stabilize the transition state energies according to a mechanism similar to those proposed by Warshel [65,66] for the stabilization of transition states in enzymatic systems. Although the rate enhancement factor of 4 observed in this switching process is not even close to the rate enhancement observed for natural enzyme systems, which are generally many orders of magnitude larger, the cooperative action of many of these stabilizing interactions could well account for a substantial part of the enzyme proficiencies.

Supplementary Materials

Supplementary materials can be accessed at: https://www.mdpi.com/1420-3049/19/4/5278/s1.

Acknowledgments

This research was supported by the European Research Council in the form of an ERC Advanced grant to R.J.M.N. (ALPROS-290886) and an ERC Starting grant to J.A.A.W.E (NANOCAT-259064). Further financial support was obtained from the Council for the Chemical Sciences of the Netherlands Organization for Scientific Research (CW-NWO) (Vidi grant for J.A.A.W.E and Vici grant for A.E.R) and from the Ministry of Education, Culture and Science (Gravity program 024.001.035).

Author Contributions

A.B.C.D., J.A.A.W.E, R.J.M.N. and A.E.R. conceived the idea. A.B.C.D. and T.W. performed the synthesis, characterization, the titration experiments and the calculations. J.M.M.S. and R.D.G. performed the X-ray structure analysis. A.B.C.D. and J.A.A.W.E. co-wrote the paper. J.A.A.W.E., R.J.M.N. and A.E.R. gave comments on the paper.

Conflicts of Interest

The authors declare no conflict of interest

References and Notes

  1. Le Gac, S.W.; Marrot, J.; Reinaud, O.; Jabin, I. Allosterically coupled double induced fit for 1+1+1+1 self-assembly of a calix[6]trisamine, a calix[6]trisacid, and their guests. Angew. Chem. Int. Ed. 2006, 19, 3123–3126. [Google Scholar]
  2. Specht, A.; Bernard, P.; Goeldner, M.; Peng, L. Mutually induced formation of host-guest complexes between p-sulfonated calix[8]arene and photolabile cholinergic ligands. Angew. Chem. Int. Ed. 2002, 41, 4706–4708. [Google Scholar] [CrossRef]
  3. Schneider, H.-J.; Güttes, D.; Schneider, U. Host guest chemistry 16. Host guest complexes with water-soluble macrocyclic polyphenolates including induced fit and simple elements of a proton pump. J. Am. Chem. Soc. 1988, 110, 6449–6451. [Google Scholar] [CrossRef]
  4. Reek, J.N.H.; Engelkamp, H.; Rowan, A.E.; Elemans, J.A.A.W.; Nolte, R.J.M. Conformational behavior and binding properties of naphthalene-walled clips. Chem.-Eur. J. 1998, 4, 716–722. [Google Scholar]
  5. Cram, D.J.; Choi, H.-J.; Bryant, J.A.; Knobler, C.B. Host-guest complexation 62. Solvophobic and entropic driving forces for forming verlcraplexes which are 4-fold, lock-key dimers in organic media. J. Am. Chem. Soc. 1992, 114, 7748–7765. [Google Scholar]
  6. Liu, Y.; Chen, Y. Cooperative binding and multiple recognition by bridged bis(beta-cyclodextrin)s with functional linkers. Acc. Chem. Res. 2006, 39, 681–691. [Google Scholar] [CrossRef]
  7. Trabolsi, A.; Urbani, M.; Delgado, J.L.; Ajamaa, F.; Elhabari, M.; Solladié, N.; Nierengarten, J.-F.; Albrecht-Gary, A.-M. Large photoactive supramolecular ensembles prepared from C(60)-pyridine substrates and multi-Zn(II)-porphyrin receptors. New J. Chem. 2008, 32, 159–165. [Google Scholar] [CrossRef]
  8. Gibson, H.W.; Yamaguchi, N.; Hamilton, L.; Jones, J.W. Cooperative self-assembly of dendrimers via pseudorotaxane formation from a homotritopic guest molecule and complementary monotopic host dendrons. J. Am. Chem. Soc. 2002, 124, 4653–4665. [Google Scholar] [CrossRef]
  9. Jones, J.W.; Zakharov, L.N.; Gibson, H.W. Cooperative host/guest interactions via counterion assisted chelation: Pseudorotaxanes from supramolecular cryptands. J. Am. Chem. Soc. 2002, 124, 13378–13379. [Google Scholar] [CrossRef]
  10. Sato, H.; Tashiro, K.; Shinmori, H.; Osuka, A.; Murata, Y.; Komatsu, K.; Aida, T. Positive heterotropic cooperativity for selective guest binding via electronic communications through a fused zinc porphyrin array. J. Am. Chem. Soc. 2005, 127, 13086–13087. [Google Scholar]
  11. Thordarson, P.; Coumans, R.G.E.; Elemans, J.A.A.W.; Thomassen, P.J.; Visser, J.; Rowan, A.E.; Nolte, R.J.M. Allosterically driven multi-component assembly. Angew. Chem. Int. Ed. 2004, 43, 4755–4759. [Google Scholar] [CrossRef]
  12. Deutman, A.B.C.; Monnereau, C.; Moalin, M.; Coumans, R.G.E.; Veling, N.; Coenen, M.; Smits, J.M.M.; de Gelder, R.; Elemans, J.A.A.W.; Ercolani, G.; et al. Squaring cooperative circles. Proc. Natl. Acad. Sci. USA 2009, 106, 10471–10476. [Google Scholar]
  13. Koshland, D.E., Jr. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. USA 1958, 44, 98–104. [Google Scholar]
  14. Steitz, T.A.; Ludwig, M.L.; Quiocho, F.A.; Lipscomb, W.N. Structure of carboxypepridase A: V. Studies of enzyme-substrate and enzyme-inhibitor complexes at 6 Å resolution. J. Biol. Chem. 1967, 242, 4662–4668. [Google Scholar]
  15. Bennett, W.S.; Huber, R. Structureal and functional aspects of domain motions in proteins. Crit. Rev. Biochem. 1984, 15, 291–384. [Google Scholar] [CrossRef]
  16. Koshland, D.E., Jr. The key-lock theory and the induced-fit theory. Angew. Chem. Int. Ed. Engl. 1994, 33, 2375–2378. [Google Scholar] [CrossRef]
  17. Gerstein, M.; Lesk, A.M.; Chothia, C. Structural mechanisms for domain movements in proteins. Biochemistry 1994, 33, 6739–6749. [Google Scholar] [CrossRef]
  18. Rebek, J., Jr.; Askew, B.; Killoran, M.; Nemeth, D.; Lin, F.-T. Convergent functional-groups. 3. A molecular cleft recognizes substrates of complementary size, shape and functionality. J. Am. Chem. Soc. 1987, 109, 2426–2431. [Google Scholar]
  19. Vicent, C.; Hirst, S.C.; Garcia-Tellado, F.; Hamilton, A.D. Conformational selectivity in molecular recognition—The influence of artificial receptors on the cis-trans isomerization of acylprolines. J. Am. Chem. Soc. 1991, 113, 5466–5467. [Google Scholar] [CrossRef]
  20. Sijbesma, R.P.; Nolte, R.J.M. A molecular clip with allosteric binding properties. J. Am. Chem. Soc. 1991, 113, 6695–6696. [Google Scholar] [CrossRef]
  21. Hayashi, T.; Asai, T.; Hokazono, H.; Ogoshi, H. Dynamic molecular recognition in a multifunctional porphyrin and a ubiquinone analog. J. Am. Chem. Soc. 1993, 115, 12210–12211. [Google Scholar] [CrossRef]
  22. Hayashi, T.; Asai, T.; Borgmeier, F.M.; Hokazono, H.; Ogoshi, H. Kinetic and thermodynamic analysis of induced-fit molecular recognition between tetraarylporphyrin and ubiquinone analogues. Chem. Eur. J. 1998, 4, 1266–1274. [Google Scholar] [CrossRef]
  23. Palyulin, V.A.; Emets, S.V.; Chertkov, V.A.; Kasper, C.; Schneider, H.-J. Conformational switching of 3,7-diacyl-3,7-diazabicyclo[3.3.1]nonanes by metal binding and by solvent changes. Eur. J. Org. Chem. 1999, 3479–3482. [Google Scholar]
  24. Weinig, H.-G.; Krauss, R.; Seydeck, M.; Bending, J.; Koert, U. Molecular signal transduction by conformational transmission: Use of tetrasubstituted perhydroanthracenes as transducers. Chem. Eur. J. 2001, 7, 2075–2088. [Google Scholar] [CrossRef]
  25. Chong, Y.S.; Smith, M.D.; Shimizu, K.D. A conformationally programmable ligand. J. Am. Chem. Soc. 2001, 123, 7463–7464. [Google Scholar] [CrossRef]
  26. Kacprzak, K.; Gawroncski, J. Bifunctional receptor triad for efficient recognition of mono- and dicarboxylic acids. Chem. Commun. 2003, 1532–1533. [Google Scholar] [CrossRef]
  27. Rebek, J., Jr. Binding forces, equilibria, and rates—New models for enzymatic catalysis. Acc. Chem. Res. 1984, 17, 258–264. [Google Scholar] [CrossRef]
  28. Takeuchi, M.; Ikeda, M.; Sugasaki, A.; Shinkai, S. Molecular design of artificial molecular and ion recognition systems with allosteric guest responses. Acc. Chem. Res. 2001, 34, 865–873. [Google Scholar] [CrossRef]
  29. Gawronski, J.; Kacprzak, K. Architecture and function of atropisomeric molecular triads. Chirality 2002, 14, 689–702. [Google Scholar] [CrossRef]
  30. Iwasawa, N.; Takahagi, H. Boronic esters as a system for crystallization-induced dynamic self-assembly equipped with an “on-off” switch for equilibration. J. Am. Chem. Soc. 2007, 129, 7754–7755. [Google Scholar] [CrossRef]
  31. Houk, K.N.; Leach, A.G.; Kim, S.P.; Zhang, X. Binding affinities of host-guest, protein-ligand, and protein-transition-state complexes. Angew. Chem. Int. Ed. 2003, 42, 4872–4897. [Google Scholar] [CrossRef]
  32. Gottwald, L.K.; Ullman, E.F. Biphenyl-type atropisomerism as a probe for coformational rigidity of alpha, beta, gamma, delta-tetraarylporphines. Tetrahedron Lett. 1969, 36, 3071–3074. [Google Scholar] [CrossRef]
  33. Walker, F.A. Biphenyl-type atropisomerism as a probe for conformational rigidity of α,β,γ,δ-tetraarylporphines. Tetrahedron Lett. 1971, 52, 4949–4952. [Google Scholar] [CrossRef]
  34. Momenteau, M.; Loock, B.; Mispelter, J.; Bisagni, E. Basket handle porphyrins and their ferrous complexes as stable oxygen carriers. Nouv. J. Chim. 1979, 3, 77–79. [Google Scholar]
  35. Momenteau, M.; Loock, B. Basket handle porphyrins—New synthetic iron(II) complexes for oxygen binding. J. Mol. Catal. 1980, 7, 315–320. [Google Scholar] [CrossRef]
  36. Jimenez, H.R.; Moratal, J.M.; Faus, J.; Momenteau, M. A solution study of the interaction of superstructured iron(II) porphyrins with catechol. New J. Chem. 1994, 18, 1247–1252. [Google Scholar]
  37. Landergren, M.; Baltzer, L. The effect of porphyrin ruffling on the intrinsic binding of carbon monoxide in iron(II) hybrid basket-handle porphyrins by multinuclear NMR and FT-IR spectroscopy. J. Chem. Soc. Perkin Trans. 2 1992, 2, 355–360. [Google Scholar] [CrossRef]
  38. Picaud, T.; le Moigne, C.; Loock, B.; Momenteau, M.; Desbois, A. Nonplanar distortions of bis-base low-spin iron(II)-porphyrinates: Absorption and resonance Raman investigations of cross-trans-linked iron(II)-basket-handle porphyrin complexes. J. Am. Chem. Soc. 2003, 125, 11616–11625. [Google Scholar]
  39. Rose, E.; Gallo, E.; Raoul, N.; Bouché, L.; Pille, A.; Caselli, A.; Lequin, O. Chiral “basket handle” binaphthyl porphyrins: Synthesis, catalytic epoxidation and NMR conformational studies. J. Porphyr. Phthalocyanines 2010, 14, 646–659. [Google Scholar] [CrossRef]
  40. Li, P.; Alenezi, K.; Ibrahim, S.K.; Wright, J.A.; Hughes, D.L.; Pickett, C.J. Towards alternatives to anodic water oxidation: Basket-handle thiolate FeIII porphyrins for electrocatalytic hydrocarbon oxidation. ChemSusChem 2012, 5, 2361–2375. [Google Scholar] [CrossRef]
  41. Elemans, J.A.A.W.; Claase, M.B.; Aarts, P.P.M.; Rowan, A.E.; Schenning, A.P.H.J.; Nolte, R.J.M. Porphyrin clips derived from diphenylglycoluril. Synthesis, conformational analysis and binding properties. J. Org. Chem. 1999, 64, 7009–7016. [Google Scholar]
  42. Elemans, J.A.A.W.; Bijsterveld, E.J.A.; Rowan, A.E.; Nolte, R.J.M. Manganese porphyrin hosts as epoxidation catalysts: Activity and stability control by axial ligand effects. Eur. J. Org. Chem. 2007, 2007, 751–757. [Google Scholar] [CrossRef]
  43. Simonis, U.; Walker, F.A.; Lee, P.L.; Hanquet, B.J.; Meyerhoff, D.J.; Scheidt, W.R. Synthesis, spectroscopic, and structural studies of extremely short chain basket handle porphyrins and their zinc(II) complexes. J. Am. Chem. Soc. 1987, 109, 2659–2668. [Google Scholar]
  44. The error obtained via measuring the integrals was significantly higher.
  45. Experimental uncertainties in van’t Hoff plots used to determine the ΔH° and ΔS° values may lead to accidental correlations with no statistical significance.
  46. Hunter, C.A.; Sanders, J.K.M. The nature of π-π interactions. J. Am. Chem. Soc. 1990, 112, 5525–5534. [Google Scholar] [CrossRef]
  47. Williams, A.R.; Northrop, B.H.; Chang, T.; Stoddart, J.F.; White, A.J.P.; Williams, D.J. Suitanes. Angew. Chem. Int. Ed. 2006, 45, 6665–6669. [Google Scholar] [CrossRef]
  48. Gunter, M.J.; Hockless, D.C.R.; Johnston, R.; Skelton, B.W.; White, A.H. Self-assembling porphyrin [2]-catenanes. J. Am. Chem. Soc. 1994, 116, 4810–4823. [Google Scholar]
  49. Gunter, M.J.; Jeynes, T.P.; Johnston, M.R.; Turner, P.; Chen, Z. Structural control of co-receptor binding in porphyrin-bipyridinium supramolecular assemblies. J. Chem. Soc. Perkin Trans. 1 1998, 1, 1945–1958. [Google Scholar]
  50. Thordarson, P.; Bijsterveld, E.J.A.; Elemans, J.A.A.W.; Kasák, P.; Nolte, R.J.M.; Rowan, A.E. Highly negative homotropic allosteric binding of viologens in a double-cavity porphyrin. J. Am. Chem. Soc. 2003, 125, 1186–1187. [Google Scholar]
  51. Unfortunately, the effect of temperature on the binding of the second molecule of V1 to S (KVSV) could therefore not be investigated.
  52. Although it could also be a result of significant 1:2 complex formation. Nevertheless, it is clear that V3 does not show significant stronger binding to C than to S.
  53. Crossley, M.J.; Field, L.D.; Forster, A.J.; Harding, M.M.; Sternhell, S. Kinetics of tautomerism in 2-substituted 5,10,15,20-tetraphenylporphyrins—Directionality of proton-transfer between the inner nitrogens. J. Am. Chem. Soc. 1987, 109, 341–348. [Google Scholar]
  54. Hatano, K.; Anzai, K.; Kubo, T.; Tamai, S. Synthesis and kinetic investigation of the atropisomerization of meso-tetra(2-cyanophenyl)porphine. Bull. Chem. Soc. Jpn. 1981, 54, 3518–3521. [Google Scholar]
  55. Hatano, K.; Anzai, K.; Nishino, A.; Fujii, K. A kinetic-study of thermal rotational isomerization of 5,10,15,20-tetrakis(ortho-aminophenyl)porphyrin and 5,10,15,20-tetrakis(ortho-pivaloylaminophenyl)porphyrin. Bull. Chem. Soc. Jpn. 1985, 58, 3653–3654. [Google Scholar] [CrossRef]
  56. Fujimoto, T.; Umekawa, H.; Nishino, N. A new picket-fence porphyrin precursor—Synthesis and atropisomerism of free base and zinc complex of meso-tetra(ortho-methoxycarbonylphenyl)porphyrin. Chem. Lett. 1992, 1992, 37–40. [Google Scholar] [CrossRef]
  57. Spasojevic, I.; Menzeleev, R.; White, P.S.; Fridovich, I. Rotational isomers of N-alkylpyridylporphyrins and their metal complexes. HPLC separation, H-1 NMR and X-ray structural characterization, electrochemistry, and catalysis of O-2(center dot-) disproportionation. J. Inorg. Chem. 2002, 41, 5874–5875. [Google Scholar]
  58. Song, R.; Robert, A.; Bernadou, J.; Meunier, B. Illustrating atropisomerism in the porphyrin series using NMR spectroscopy. Analusis 1999, 27, 464–467. [Google Scholar]
  59. Reginato, G.; di Bari, L.; Salvadori, P.; Guilard, R. Chiral atropisomeric metalloporphyrins in the enantioselective styrene epoxidation. Eur. J. Org. Chem. 2000, 2000, 1165–1171. [Google Scholar] [CrossRef]
  60. Coumans, R.G.E.; Elemans, J.A.A.W.; Nolte, R.J.E.; Rowan, A.E. Processive enzyme mimic. Kinetics and thermodynamics of the threading and sliding process. Proc. Natl. Acad. Sci. USA 2006, 103, 19647–19651. [Google Scholar] [CrossRef]
  61. Sheldrick, G.M. SADABS. Program for Emperical Absorption Correction; University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
  62. De Gelder, R.; de Graaff, R.A.G.; Schenk, H. Automatic determination of crystal structures using Karle-Hauptman matrices. Acta Cryst. 1993, A49, 287–293. [Google Scholar] [CrossRef]
  63. Sheldrick, G.M. SHELXL-97. Program for the Refinement of Crystal Structures; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
  64. These data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html or from the CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44 1223 336033; E-Mail: [email protected].
  65. Warshel, A. Computer Modeling of Chemical Reactions in Enzymes and Solutions; Wiley: New York, NY, USA, 1991. [Google Scholar]
  66. Warshel, A. Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites. J. Biol. Chem. 1998, 273, 27035–27038. [Google Scholar] [CrossRef]
  • Sample Availability: Not available.

Share and Cite

MDPI and ACS Style

Deutman, A.B.C.; Woltinge, T.; Smits, J.M.M.; De Gelder, R.; Elemans, J.A.A.W.; Nolte, R.J.M.; Rowan, A.E. Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers. Molecules 2014, 19, 5278-5300. https://doi.org/10.3390/molecules19045278

AMA Style

Deutman ABC, Woltinge T, Smits JMM, De Gelder R, Elemans JAAW, Nolte RJM, Rowan AE. Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers. Molecules. 2014; 19(4):5278-5300. https://doi.org/10.3390/molecules19045278

Chicago/Turabian Style

Deutman, Alexander B. C., Tim Woltinge, Jan M. M. Smits, René De Gelder, Johannes A. A. W. Elemans, Roeland J. M. Nolte, and Alan E. Rowan. 2014. "Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers" Molecules 19, no. 4: 5278-5300. https://doi.org/10.3390/molecules19045278

APA Style

Deutman, A. B. C., Woltinge, T., Smits, J. M. M., De Gelder, R., Elemans, J. A. A. W., Nolte, R. J. M., & Rowan, A. E. (2014). Thermodynamics and Kinetics of Guest-Induced Switching between “Basket Handle” Porphyrin Isomers. Molecules, 19(4), 5278-5300. https://doi.org/10.3390/molecules19045278

Article Metrics

Back to TopTop