1. Introduction
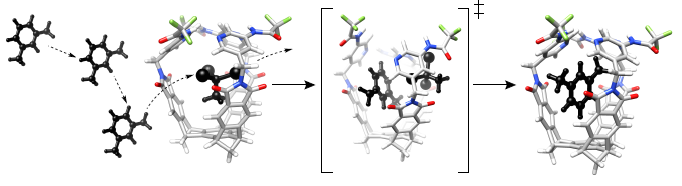
The process of molecular encapsulation occurs, in concave hosts, via slippage, gating or full dissociation of self-assembled components [
1]. Indeed, elucidating the mechanism of the operation of cavitands [
2,
3,
4,
5] has been an interest for controlling the outcome of chemical reactions [
6], stabilizing reactive intermediates [
7], or delivering useful molecules [
8,
9]. Accordingly, for the complexation of metal cations with crown ethers, Schneider and Cox reported that the rates by which cations access (
kin) the macrocycles are fast (approaching a diffusion-controlled limit) while their departure from the complex (
kout) is much slower corresponding to the thermodynamic stability (∆
G°) of the complex itself [
10]. Importantly, the corresponding mechanistic study [
11] indicated an early transition state for the entrapment, resembling reactants to account for the absence of the selectivity in complexation events. For gated molecular encapsulations [
12], however, a conformational change in a gated host creates an aperture permitting in/out exchange of guests. The complexation is, for this reason, occurring at a slower rate with the corresponding higher activation barrier referred to as constrictive binding [
13]. As a result, one could tune the kinetics of molecular encapsulation by controlling conformational changes of the host [
14]. Furthermore, the “opening” of some dynamic hosts, hemicarcerans [
15,
16] or self-folding capsules [
17], were argued to constitute the rate-determining step of encapsulation. In other gating situations [
18,
19], however, the guest entrance generates enough van der Waals strain so that the encapsulation rate law exhibits a kinetic dependence in the concentration of both host and guest [
20]. To our knowledge, there has been no particular study [
21] about the nature of transition states characterizing gated encapsulations, and this is the objective of our paper.
Gated molecular baskets [
22] have been designed and studied in our laboratory for almost a decade [
23]. These hosts comprise a flat aromatic base that is fused to three bicycle[2.2.1]heptane rings forming a curved unit (V = 220 Å
3,
Figure 1).
Figure 1.
Energy-minimized (MMFFs, Spartan) and chemical structures of gated molecular basket 1 (V = 220 Å3). The kinetics of in/out trafficking of guest 2 (V = 107 Å3) to (kin) and from (kout) basket 1 was studied in solvents 3–6 (99–154 Å3).
Figure 1.
Energy-minimized (MMFFs, Spartan) and chemical structures of gated molecular basket 1 (V = 220 Å3). The kinetics of in/out trafficking of guest 2 (V = 107 Å3) to (kin) and from (kout) basket 1 was studied in solvents 3–6 (99–154 Å3).
Three phthalimides extend this structure into a bowl-shaped platform. Three aminopyridine rings [
24], containing hydrogen-bonding donor and acceptor sites, are attached to the rim of the platform to, via CH
2 “hinges”, act as gates that, by controlling the portal size, regulate the in/out encapsulation of small haloalkanes (V ~ 88–120 Å
3) [
25]. The formation of basket/guest complex was, in solvophobic CD
2Cl
2 solvent (V = 61 Å
3) [
26], found to be first- while the dissociation is zeroth-order in guests (
Figure 1) [
20]. In essence, the basket undergoes a rapid thermal racemization (∆
G‡rac < 11 kcal/mol) to, occasionally, permit the entrance/departure of guest molecules [
27]. For a series of isosteric guests we found a linear dependence between the host-guest affinities (∆
G°) and the free energies of activation (∆
G‡in and ∆
G‡out), which was fit to the following equation: ∆
G‡in/out = ρ
in/out∆
G° + δ [
28] On the basis of rather small ρ
in values (0.08–0.25), we hypothesized that an early transition state characterizes gated encapsulations [
27,
28]; this was additionally supported with a relatively poor stereo-selectivity of entrapments (
kinR/
kinS ~ 2–3) [
29].
To investigate the nature of the transition state of gated molecular encapsulations in greater details, we hereby used dynamic
1H-NMR spectroscopy to measure rate coefficients (
kout) by which 1,1,1-tribromoethane
2 (V = 107 Å
3) departs from the interior of basket
1 in four aromatic solvents
3–
6 (
Figure 1). In earlier studies [
20], we surmised that the egress of guest molecule should be followed with the entrapment of solvent (
Figure 1). It follows that the rate of such guest swap should change with increasingly bigger solvent molecules (99–154 Å
3,
Figure 1) via a steric imposition of the transition state of the transformation [
21,
30].
2. Results and Discussion
Basket
1 (
Figure 1) was prepared by following an optimized synthetic procedure [
14]. It was poorly soluble in
m-xylene-d
10 (
vide supra) forming a suspension at 298.0–348.0 K (
Figure S1). Upon addition of 1,1,1-tribromoethane
2 (0.8–50 molar equivalents,
Figure S4), however, the solid basket
1 was extracted into
m-xylene-d
10 to, perhaps, give a [
1–
2] complex. Indeed, the formation of [
1–
2] ensued on the basis of
1H-NMR spectroscopy and the intensity of signals corresponding to both host and guest (
Figure 2A). DOSY NMR spectroscopic measurements (
Figures S6–S9) were also in line with the formation of 1:1 complex in each solvent (
rH ~ 7–8 Å,
Table 1) [
31]; the experimental hydrodynamic radii correspond to the computed size (
d ~ 14 Å, MMFFs) of [
1–
2] complex. Furthermore, two separate
1H- singlets corresponding to the guest inside the host (δ = −1.34 ppm,
Figure 2A) and in bulk solvent (δ = 2.81 ppm,
Figure 2A) suggested a slow in/out exchange of CH
3CBr
3 occurring at 300.1 K on the “time scale. Accordingly, we completed
1H,
1H–EXSY NMR measurements (400 MHz, 300.1 K) to examine the kinetics characterizing the trafficking of complexed guest [
2]
in into bulk solvent [
2]
out (
kout,
Figure 2A); note that due to the nature of EXSY experiment [
32], the experimentally determined rate coefficient
kout * is pseudo first-order in character (s
−1,
Table 1) and in line with the rate
vout * =
kout * [
1–
2]. On the basis of the reaction’s stoichiometry, however, the reaction’s rate could be
vout =
kout [
1–
2] (
Figure 2A) and it follows that
kout * =
kout as long as the proposed model is valid. Since greater concentrations of guest [
2] in solution (3.0–22.0 molar equivalents) had no measurable effects on the experimental rate constant
kout * (
Figure 2B) we conclude that the process of decomplexation is zeroth-order in 1,1,1-tribromoethane
2 [
20]. This, in turn, corroborates the absence of interchange mechanism (
Figure 2C) [
19], whereby free guests substitute the one of the same kind trapped in the host. Alternatively, a molecule of solvent
5 could approach [
1–
2] to via its sizeable side aperture “push” the encapsulated guest out and thereby give complex [
1–
5] (
Figure 2D); note that, in this situation [
28], the gates ought to “open” so that the substitution takes place. In line with this mechanistic hypothesis, varying the size of solvent molecules should have an effect on the rate by which guest
2 departs the basket: more sizeable compounds should create a greater van der Waals strain, while entering or exiting the host (vide infra), to affect the in/out exchange! Accordingly, we measured (
1H,
1H–EXSY 300.1 K) rate coefficients
kout corresponding to 1,1,1-tribromoethane
2 departing from [
1–
2] complex in three additional solvents: Benzene-d
6 (
3), toluene-d
8 (
4) and mesitylene-d
12 (
6). The rate coefficients
kout were, importantly, found to increase (while
kin decreased) for smaller solvents (
Table 1). In fact, there exists a linear free energy relationship (LFER) with log
kout being proportional to the volume of solvent molecules (
R2 = 0.97,
Figure 3A).
Figure 2.
(A) 1H-NMR spectrum (400 MHz, 300.1 K) of C3 symmetric basket 1 (0.5 mg) suspended in m-xylene-d10 and containing guest 2 (6.5 mM); (B) A plot showing experimental rate coefficients kout * (s−1), obtained from 1H,1H–EXSY NMR (400 MHz) measurements, as a function of the concentration of guest 2 with basket 1 (1.1 mg) in m-xylene-d10 at 300.1 K; The interchange ((C), MMFFs/Spartan) or solvent-displacement ((D), MMFFs/Spartan) mechanisms of the exchange).
Figure 2.
(A) 1H-NMR spectrum (400 MHz, 300.1 K) of C3 symmetric basket 1 (0.5 mg) suspended in m-xylene-d10 and containing guest 2 (6.5 mM); (B) A plot showing experimental rate coefficients kout * (s−1), obtained from 1H,1H–EXSY NMR (400 MHz) measurements, as a function of the concentration of guest 2 with basket 1 (1.1 mg) in m-xylene-d10 at 300.1 K; The interchange ((C), MMFFs/Spartan) or solvent-displacement ((D), MMFFs/Spartan) mechanisms of the exchange).
Figure 3.
(A) A plot showing log kout as function of van der Waals volume (Spartan) of solvents 3–6. The data was fit to a linear function using the least-square method of analysis (R2 = 0.97, Sigma Plot); (B) A plot showing log kout as function of the stability log Ka of [1–2] complex in solvents 3–6. The data was fit to a linear function using the least-square method of analysis (R2 = 0.94, Sigma Plot); (C) A plot showing showing log Ka as function of the solubility log S of [1–2] complex in solvents 3–6. The data was fit to a linear function using the least-square method of analysis (R2 = 0.94, Sigma Plot); (D) Reaction coordinate diagram showing the relative stability of [1–solvent] complexes.
Figure 3.
(A) A plot showing log kout as function of van der Waals volume (Spartan) of solvents 3–6. The data was fit to a linear function using the least-square method of analysis (R2 = 0.97, Sigma Plot); (B) A plot showing log kout as function of the stability log Ka of [1–2] complex in solvents 3–6. The data was fit to a linear function using the least-square method of analysis (R2 = 0.94, Sigma Plot); (C) A plot showing showing log Ka as function of the solubility log S of [1–2] complex in solvents 3–6. The data was fit to a linear function using the least-square method of analysis (R2 = 0.94, Sigma Plot); (D) Reaction coordinate diagram showing the relative stability of [1–solvent] complexes.
To additionally probe the nature of the encapsulation events at hand, we used
1H-NMR spectroscopy to quantify the affinity (
Ka, M
−1) of basket
1 for trapping
2 in each solvent (
Table 1). The binding was found to be strongest in “large” mesitylene-d
12 (V = 154 Å
3) while weakest in “small” benzene-d
6 (V = 99 Å
3) [
26]. The measured affinity constants (
Ka,
Table 1) suggest for the stability of [
1–
solvent] complexes to be in the order: [
1–
6] < [
1–
5] < [
1–
4] < [
1–
3] (
Figure 3D). In other words, the stability of [
1–
2] could be comparable in solvents
3–
6, having ε ~ 2–4 (
Figure 3D) [
33]. To further investigate this point of view, we used
19F-NMR spectroscopy (with C
6F
6 as internal standard,
Figure S14) to quantify the solubility (
S,
Table 1) of basket
1 in solvents
3–
6. The solubility delineates a dynamic equilibrium between basket
1 in its solid state (always the same in any solvent) and as solute in solution and is thus proportional to the stability of [
1–
solvent] complexes. As log (
S) commensurates with log
Ka (
Figure 3C), we conclude that in these two experiments the stability of [
1–
solvent] complexes primarily determines the state of each equilibrium. Consequently, the stability of [
1–
2] complex is, in aromatic solvents
3–
6, comparable and therefore shown in
Figure 3D as one state. At last, the experimental order of stability of [
1–
solvent] complexes tracks an increased population of the inner space of basket
1 (approximated
PCs are given in
Table 1) [
26].
Table 1.
Diffusion coefficients (
D) of [
1–
2] complex were obtained from DOSY NMR (400 MHz) at 300.1 K and converted into hydrodynamic radii (
rH) using the Stokes-Einstein equation. The exchange rate constants
kout (
s−1) were obtained from
1H,
1H–EXSY NMR (300.1 K) and are shown as mean ± standard deviation (>10 measurements). The equilibrium constants
Ka (M
−1) were estimated from
1H NMR spectroscopic measurements (via signal integration) at 300.1 K, while
kin was calculated as
kin =
Ka kout. Solubility (
S) of basket
1, in
3–
6, was determined with the assistance of
19F NMR spectroscopy at 300.1 K. Packing coefficients (PC) were calculated as
PC (%) =
Vguest/
Vhost’s inner space [
26].
Table 1.
Diffusion coefficients (D) of [1–2] complex were obtained from DOSY NMR (400 MHz) at 300.1 K and converted into hydrodynamic radii (rH) using the Stokes-Einstein equation. The exchange rate constants kout (s−1) were obtained from 1H,1H–EXSY NMR (300.1 K) and are shown as mean ± standard deviation (>10 measurements). The equilibrium constants Ka (M−1) were estimated from 1H NMR spectroscopic measurements (via signal integration) at 300.1 K, while kin was calculated as kin = Ka kout. Solubility (S) of basket 1, in 3–6, was determined with the assistance of 19F NMR spectroscopy at 300.1 K. Packing coefficients (PC) were calculated as PC (%) = Vguest/Vhost’s inner space [26].
| | C6D6 (3) | C6D5CD3 (4) | C6D4 (CD3)2 (5) | C6D3 (CD3)3 (6) |
|---|
| D (10−10 m2s−1) | 4.7 ± 0.1 | 5.9 ± 0.2 | 4.47 ± 0.06 | 4.21 ± 0.03 |
| rH (Å) | 7.7 | 6.7 | 8.5 | 8.0 |
| kout (s−1) | 19.2 ± 2.2 | 11.8 ± 1.6 | 8.3 ± 1.3 | 3.6 ± 0.8 |
| Ka (M−1) | 32 | 390 | 637 | 4123 |
| kin (M−1s−1) | [6.1 ± 0.7] × 102 | [4.6 ± 0.6] × 103 | [5.3 ± 0.8] × 103 | [1.5 ± 0.3] × 104 |
| S (µmol/dm3) | 108 ± 11 | 83 ± 8 | 35 ± 4 | 19 ± 2 |
| PC (%) | 45 | 53 | 62 | 70 |
Evidently, more favorable decomplexations of [
1–
2] (smaller log
Ka,
Figure 3B) are, in solvents
3–
6, occurring at a faster rate (bigger log
kout). The slope of the linear log
Ka/log
kout function (
Figure 3B) is equal to 0.3 (
Figure 3B), with a greater span of ∆
G° (∆∆
G° ~ 3 kcal/mol) than ∆
G‡out (∆
G‡out ~ 1 kcal/mol) values, along the series. On the basis of the transition state theory, ∆
G‡out corresponds to the equilibrium between ([
1–
2] + [
solvent]) and [
solvent–
1–
2]
‡ whereas ∆
G° describes the balance between ([
1–
2] + [
solvent]) and ([
1–
solvent] + [
2]). Since the initial states are for both processes the same and comparable in energy (
Figure 3D), the observed LFER in
Figure 3B must indicate a greater span in the stability of [
1–
solvent] complexes than the corresponding transition states [
solvent–
1–
2]
‡ (
Figure 4A)! To partly account for the observation, we note that the transition state for gated exchange must be an “open” form of the basket with (a) no intramolecular hydrogen bond(s) and (b) somewhat extended surface. Such transient species should “more easily” accommodate differently sized and shaped solvents, than [
1–
solvent] complex having a “closed” surface, to give rise to a more narrow distribution of ∆
G‡out values.
The energy separation between [
solvent–
1–
2]
‡ and the corresponding ground states is rather large (>10 kcal/mol,
Figure 4A) and in line with a unique structure of this fleeting complex lacking N-H-N intramolecular hydrogen bonds [
34]. With the assistance of
1H,
1H–EXSY spectroscopy, we measured rate coefficients
kout characterizing the departure of
2 from [
1–
2] at various temperatures in
m-xylene-d
10 (
Table S5). From the Eyring plot (
Figure 4B), we determined the activation parameters ∆
H‡ = 10 ± 1 kcal/mol and ∆
S‡ = −21 ± 4 kcal/mol K characterizing the process [
21]. The negative entropy of activation (∆
S‡ < 0) is indeed in line with an associative mechanism of exchange, resembling classical S
N2 reactions, with simultaneous (but not necessarily synchronous) egress of
2 and ingress of
m-xylene-d
10 (
Figure 4C)! In spite of the postulated one-step mechanism (
Figure 2D), the exchange process may also be a two-step process including rapid opening of the basket’s one gate (first step) followed by a slower swapping of the entrapped with the incoming compounds and the simultaneous opening of two additional gates (second step). It is indeed difficult to repudiate this particular mechanistic scenario, although we have not observed any intermediate either spectroscopically or kinetically (the saturation kinetics) [
18] to suggest the two-step process [
23]. In addition, en earlier study [
26] indicated that for a guest populating the basket’s inner space to a greater extent (PC > 0.3,
Table 1) the basket’s racemization necessitates simultaneous opening of all three gates.
Figure 4.
(A) A reaction coordinate diagram depicting kinetic and thermodynamic characteristics of the encapsulation; (B) The Eyring plot showing log kout/T as function of 1/T corresponding to the decomplexation of [1–2] complex in m-xylene-d10. The data was fit to a linear function using the least-square method of analysis (R2 = 0.98, SigmaPlot); (C) The energy minimized [5–1–2]‡ complex (MMFFs, Spartan) showing m-xylene-d10 entering while 1,1,1-tribromoethane 2 exiting the basket’s inner space.
Figure 4.
(A) A reaction coordinate diagram depicting kinetic and thermodynamic characteristics of the encapsulation; (B) The Eyring plot showing log kout/T as function of 1/T corresponding to the decomplexation of [1–2] complex in m-xylene-d10. The data was fit to a linear function using the least-square method of analysis (R2 = 0.98, SigmaPlot); (C) The energy minimized [5–1–2]‡ complex (MMFFs, Spartan) showing m-xylene-d10 entering while 1,1,1-tribromoethane 2 exiting the basket’s inner space.
To assess possible changes in the structure of the transition states for the postulated displacement mechanism (
Figure 2D), we used the More O’Ferrall-Jencks diagram (
Figure 5) [
35]. Three reaction coordinates, as in classical nucleophilic substitutions [
36], are included: (a) x-axis presents the solvent encapsulation without guest departure; (b) y-axis depicts the sole departure of guest (akin to S
N1); and (c) the diagonal coordinate is a combination of the two pathways (akin to S
N2). The movement of the transition state, with a change in the potential energy of the system (z-axis), proceeds along the diagonal reaction coordinate (Hammond effect) but, in accord with this approach, should also be balanced with a shift perpendicular to it (anti-Hammond effect) [
36].
Bulkier solvent molecules form less stable complexes with basket
1 so that the top and bottom right corners are, in
Figure 5, raised in the series
3–
6. Accordingly, the transition state shifts along AB and AC vectors to give rise to the AD vector. It follows that with an increase in the solvent size, the degree of solvent encapsulation stays constant while the magnitude of the guest departure increases. To put it in the language of classical organic chemistry, bulkier solvents enforce “S
N1-like” mechanism of the supramolecular substitution: More sizeable mesitylene-d
12 pushes the departing 1,1,1-tribromoethane
2 to a greater degree than benzene-d
6 in the transition state [
36,
37]. The analysis is reasonable since bigger mesitylene-d
12 provides less space than smaller benzene-d
6 for departing compound
2 within the limited inner space of basket
1. At last, the LFER in
Figure 3A shows a linear dependence for the rate of the guest departure (log
kout) as a function of the size (“nucleophilicity”) of solvents
3–
6 thereby supporting the More O’Ferrall-Jencks analysis in
Figure 5. In fact, this plot is analogous to Brönsted relationships [
37] (log
k = β
Nuc·p
Ka + n) that are used for characterizing the degree of covalent bond formation (β
Nuc; which is the degree of solvent’s encapsulation in our case) in the transition state of substitution reactions as a function of nucleophilicity [
35].
Figure 5.
A More O’Ferrall-Jencks plot for solvents 3–6 (only 5 is shown) displacing 1,1,1-tribromoethane 2 in basket 1.
Figure 5.
A More O’Ferrall-Jencks plot for solvents 3–6 (only 5 is shown) displacing 1,1,1-tribromoethane 2 in basket 1.
3. Experimental Section
All chemicals were purchased from commercial sources, and used as received unless stated otherwise. Solvents
3,
4 and
6 were purchased from Cambridge Isotope Laboratories: benzene-d
6 (D-99.5%), toluene-d
8 (D-99.5%) and mesitylene-d
12 (D-98%).
m-Xylene-d
10 (D-98%) was obtained from Sigma-Aldrich. All solvents (used in synthesis, see Scheme in
supporting information) were dried prior to use according to standard literature protocols. Chromatography purifications were performed using silica gel 60 (Sorbent Technologies 40–75 μm, 200 × 400 mesh). Thin-layer chromatography (TLC) was performed on silica-gel plate w/UV254 (200 μm).
1H and
13C-NMR spectra were recorded (400 and 100 MHz, respectively), on a Bruker DPX-400 spectrometer unless otherwise noted.
19F NMR spectra were performed (376.54 MHz) on Bruker Biospin spectrometer with hexafluorobenzene (C
6F
6) as internal standard. All spectra were referenced using the solvent residual signal. The chemical shift values are expressed as δ (ppm) values. Coupling patterns are abbreviated as s (singlet), d (doublet), t (triplet), m (multiplet)
. Temperatures for all NMR measurements were calibrated with neat methanol as a standard. High-resolution mass spectrometric measurements were completed on Bruker Micromass Q-TOF II spectrometer.
Compound
S2 (see
Scheme S1 in SI): A solution of bromine (0.52 g, 3.3 mmol) in CCl
4 (7 mL) was added to a solution of compound
S1 (1.0 g, 3.0 mmol) in CCl
4 (20 mL) over 5 min at 77 °C. Following, the solvent was removed under reduced pressure to give brown oil. The oil was loaded on a thin pad of silica (SiO
2), and then washed with dichloromethane (100 mL). The solvent was removed under reduced pressure to give compound
S2 as a light yellow solid (1.5 g, 99% yield; 2:1 mixture of two diastereomers).
1H NMR (400 MHz, CDCl
3): δ (ppm) = 7.76–7.61 (m, 2 H, Ar
H), 5.33 (d,
J = 4.0 Hz, 0.3 H, C
H), 4.45 (d,
J = 2.8 Hz, 0.7 H, C
H), 3.93 (s, 6 H, 2 × C
H3), 2.83(m, 0.7 H, C
H2), 2.72 (d,
J = 8.1 Hz, 0.3 H, C
H2), 2.38 (m, 0.3 H, C
H2), 2.28 (m, 0.7 H, C
H2).
13C NMR (100.62 MHz, CDCl
3): δ (ppm) = 168.05, 168.01, 167.98, 167.68, 147.63, 146.94, 146.67, 145.67, 132.60, 131.50, 131.30, 131.27, 125.47, 125.14, 124.87, 122.05, 67.27, 66.90, 65.07, 63.69, 63.25, 63.11, 55.42, 52.94, 52.93, 52.88, 52.44, 47.23, 46.78. HRMS (ESI)
m/z calcd for C
15H
13Br
3O
4Na [M+Na]
+ 516.8256, found 516.8272.
Compound
S3 (see
Scheme S1 in SI): A solution of potassium
tert-butoxide (0.65 g, 1.3 mmol) in dry THF (20 mL) was added, by a syringe pump (3 h), to a stirred solution of compound
S2 (0.22 g, 2.0 mmol) in dry THF (100 mL) at 0 °C. After the addition was complete, the reaction mixture was stirred for additional 2 h at 0 °C. Following, the reaction mixture was quenched with cold acidic water (HCl aq), and the solvent evaporated under reduced pressure. The solid residue was partitioned between water (100 mL) and ethyl acetate (3 × 80 mL). Combined organic layers were dried over Na
2SO
4 and then evaporated under reduced pressure. The solid residue was purified by column chromatography (SiO
2, hexane/ethyl acetate = 3:1) to yield compound
S3 as a white solid (0.43 g, 80% yield); m.p. 110–111 °C.
1H-NMR (400 MHz, CDCl
3): δ (ppm) = 7.65 (s, 2 H, 2 × C
H), 4.00 (m, 2 H, 2 × C
H), 3.90 (s, 6 H, 2 × C
H3), 2.79 (m, 1 H, C
H2), 2.42 (m, 1 H, C
H2).
13C NMR (100.62 MHz, CDCl
3): δ (ppm) = 166.78, 150.38, 132.01, 128.90, 120.85, 65.69, 57.30, 51.40. HRMS (ESI)
m/z calcd for C
15H
12Br
2O
4Na [M+Na]
+ 438.8975, found 438.8972.
Compound
S4 (see
Scheme S1 in SI): A solid mixture of Pd(OAc)
2 (57 mg, 0.25 mmol), Ph
3P (0.13 g, 0.51 mmol), Bu
4NBr (1.7 g, 5.1 mmol), K
2CO
3 (3.5 g, 25.4 mmol) and 4Å molecular sieves (4.7 g) was added to a solution of dry dioxane (100 mL) under an atmosphere of argon. Compound
S3 (0.53 g, 1.3 mmol) was added and the reaction mixture stirred at 100 °C for additional 48 h. After, the reaction suspension was cooled to a room temperature and filtered with a filter paper. The solid residue was washed with ethyl acetate (~150 mL), and the organic solvent evaporated under reduced pressure to yield a crude solid residue. The residue was partitioned between water (100 mL) and ethyl acetate (3 × 80 mL). Combined organic layers were evaporated under vacuum, and the solid residue purified by column chromatography (SiO
2, hexane/ethyl acetate = 2:1) to yield compound
S4 (59 mg, 20% yield); note that
anti stereoisomer of
S4 was also isolated (60 mg, 20% yield).
1H-NMR (400 MHz, CDCl
3): δ (ppm) = 7.43 (s, 6 H, 6 × C
H), 4.41 (s, 6 H, 6 × C
H), 3.78 (s, 18 H, 6 × C
H3), 2.52 (m, 6 H, 3 × C
H2).
1H-NMR of
anti diastereomer of
S4 (400 MHz, CDCl
3): δ (ppm) = 7.64 (s, 2 H, 2 × C
H), 7.54 (s, 2 H, 2 × C
H), 7.51 (s, 2 H, 2 × C
H), 4.40 (s, 2 H, 2 × C
H), 4.37, (s, 2 H, 2 × C
H), 4.36 (s, 2 H, 2 × C
H), 3.81–3.90 (s, 18 H, 2 × C
H3), 2.48 (m, 2 H, C
H2), 2.44 (m, 1 H, C
H2), 2.37 (m, 2 H, C
H2), 2.24 (m, 1 H, C
H2).
The supplementary information includes: 1H-NMR Binding Studies, DOSY NMR/1H, 1H-EXSY spectroscopic measurements, variable temperature NMR measurements and 19F-NMR quantification of the solubility of basket 1.