Hydration and Ion Pair Formation in Aqueous Lu3+- Solution
Abstract
:1. Introduction
2. Experimental Details; Data Analysis and DFT Calculations on Lu3+-Water Hydrates
2.1. Preparation of Solutions
2.2. Spectroscopic Measurements:
2.3. Quantitative Raman Measurements
2.4. DFT Calculations
3. Results
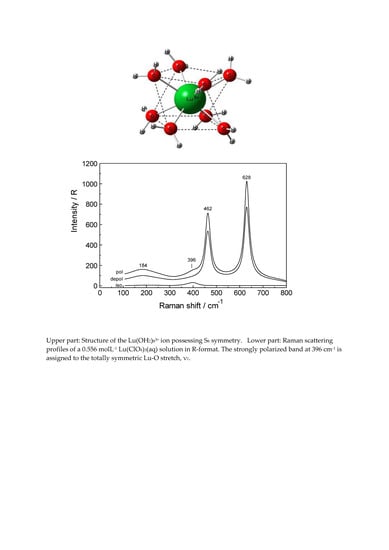
3.1. The [Lu(OH2)8]3+ (aq) Ion
3.2. Lu(ClO4)3 and Lu(CF3SO3)3 Solutions in Water and Heavy Water
3.3. Lu3+- Trifluorosulfonate in Aqueous Solution
3.4. LuCl3 (aq)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Hydration Enthalpy: Comparison of Calculated Values with Experimental Ones
with ΔHcluster = H[Lu(OH2)8]3+ − H(Lu3+) – 8 × H(OH2)
Appendix B
Accuracy of the DFT Method
References
- Taylor, S.; McClennan, S. The Continental Crust: Its Composition and Evolution; Blackwell Scientific Publications: Oxford, UK, 1985. [Google Scholar]
- Cotton, S. Lanthanide and Actinide Chemistry; John Wiley & Sons: Chichester, West Sussex, UK, 2006. [Google Scholar]
- Emsley, J. Nature’s Building Blocks: An A-Z Guide to the Elements, Lutetium; Oxford University Press: Oxford, UK, 2011; pp. 240–242. [Google Scholar]
- Huang, C.-H.; Bian, Z. Introduction in Rare Earth Coordination Chemistry: Fundamentals and Applications; Huang, C.-H., Ed.; John Wiley & Sons Wiley: Chichester, West Sussex, UK, 2010. [Google Scholar]
- Zimmerman, P.A.; Rice, B.J.; Piscanib, E.C.; Liberman, V. Optical Microlithography XXII; Levinson, H.J., Dusa, M.V., Eds.; Proc. of SPIE: Bellingham, WA, USA, 2009; Volume 7274-11, p. 727420. [Google Scholar]
- Yao, R.; Ma, T.; Shao, Y. Lutetium oxyorthosilicate (LSO) intrinsic activity correction and minimal detectable target activity study for SPECT imaging with a LSO-based animal PET scanner. Phys. Med. Biol. 2008, 53, 4399. [Google Scholar] [CrossRef] [PubMed]
- Lapen, T.J.; Righter, M.; Brandon, A.D.; Debaille, V.; Beard, B.L.; Shafer, J.T.; Peslier, A.H. A Younger Age for ALH84001 and Its Geochemical Link to Shergottite Sources in Mars. Science 2010, 328, S347–S351. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, K.M.; Collins, S.M.; Fenwick, A.J. International Conference on Nuclear Data for Science and Technology. In Proceedings of the EPJ Web of Conferences, Bruges, Belgium, 11–16 September 2016; ND 2016, p. 08002-5. [Google Scholar]
- U.S. Food & and Drug Administration. January 2018. Available online: https://www.fda.gov/Drugs/.../ApprovedDrugs/ucm594105.htm. (accessed on 26 January 2018).
- Krishnamurthy, N.; Gupta, C.K. Extractive Metallurgy of Rare Earths, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Brown, P.L.; Ekberg, C. Hydrolysis of Metal Ions, 1st ed.; Wiley-VCH: Weinheim, Germany, 2016. [Google Scholar]
- Spedding, F.H.; Pikal, M.; Ayers, B. Apparent Molal Volumes of Some Aqueous Rare Earth Chloride and Nitrate Solutions at 25°. J. Phys. Chem. 1966, 70, 2440–2449. [Google Scholar] [CrossRef]
- Spedding, F.H.; Shiers, L.E.; Brown, M.A.; Derer, J.L.; Swanson, D.L.; Habenschuss, A.J. Densities and apparent molal volumes of some aqueous rare earth solutions at 25.deg. II. Rare earth perchlorates. J. Chem. Eng. Data 1975, 20, 81–88. [Google Scholar] [CrossRef]
- Spedding, F.H.; Cullen, P.F.; Habenschuss, A. Apparent molal volumes of some dilute aqueous rare earth salt solutions at 25.deg. J. Phys. Chem. 1974, 78, 1106–1110. [Google Scholar] [CrossRef]
- Cossy, C.; Merbach, A.E. Recent Developments in Solvation and Dynamics of the Lanthanide (III) Ions. Pure Appl. Chem. 1988, 60, 1785–1796. [Google Scholar] [CrossRef]
- Persson, I.; D’Angelo, P.; Panifilis, S.D.; Sandström, M.; Eriksson, L. Hydration of Lanthanoid(III) Ions in Aqueous Solution and Crystalline Hydrates Studied by EXAFS Spectroscopy and Crystallography: The Myth of the “Gadolinium Break”. Chem.-Eur. J. 2008, 14, 3056–3066. [Google Scholar] [CrossRef]
- D’Angelo, P.; Spezia, R. Hydration of Lanthanoids(III) and Actinoids(III): An Experimental/Theoretical Saga. Chem. -Eur. J. 2012, 18, 11162–11178. [Google Scholar] [CrossRef] [PubMed]
- Duvail, M.; D’Angelo, P.; Gaigeot, M.-P.; Vitorge, P.; Spezia, R. What first principles molecular dynamics can tell us about EXAFS spectroscopy of radioactive heavy metal cations in water. Radiochim. Acta 2009, 97, 339–346. [Google Scholar] [CrossRef]
- Zhang, J.; Heinz, N.; Dolg, M. Understanding Lanthanoid(III) Hydration Structure and Kinetics by Insights from Energies and Wave functions. Inorg. Chem. 2014, 53, 7700–7708. [Google Scholar] [CrossRef] [PubMed]
- Hitzenberger, M.; Hofer, T.; Weiss, A. Solvation properties and behaviour of lutetium(III) in aqueous solution—A quantum mechanical charge field (QMCF) study. J. Chem. Phys. 2013, 139, 114306-7. [Google Scholar] [CrossRef] [PubMed]
- Sessa, F.; Spezia, R.; D’Angelo, P. Lutetium(iii) aqua ion: On the dynamical structure of the heaviest lanthanoid hydration complex. J. Chem. Phys. 2016, 144, 204505. [Google Scholar] [CrossRef] [PubMed]
- Ishiguro, S.-I.; Umebayashi, Y.; Kato, K.; Takahashib, R.; Ozutsumi, K. Strong and weak solvation steric effects on lanthanoid(III) ions in N,N-dimethylformamide-N,N-dimethylacetamide mixtures. J. Chem. Soc., Faraday Trans. 1998, 94, 3607–3612. [Google Scholar] [CrossRef]
- Yaita, T.; Narita, H.; Suzuki, S.; Tachimori, S.; Motohashi, H.; Shiwaku, H. Structural study of lanthanides(III) in aqueous nitrate and chloride solutions by EXAFS. J. Radioanal. Nucl. Chem. 1999, 239, 371–375. [Google Scholar] [CrossRef]
- Rogers, R.D.; Kurihara, L.K. f-element/crown ether complexes. 6. Interaction of hydrated lanthanide chlorides with 15-crown-5: Crystallization and structures of [M(OH2)8]Cl3·(15-crown-5) (M = Gd, Lu). Inorg. Chim. Acta 1987, 130, 131–137. [Google Scholar] [CrossRef]
- Habenschuss, A.; Spedding, F.H. The coordination (hydration) of rare earth ions in aqueous chloride solutions from x ray diffraction. I. TbCl3, DyCl3, ErCl3, TmCl3,and LuCl3. J. Chem. Phys. 1979, 70, 2797–2806. [Google Scholar] [CrossRef]
- Migliorati, V.; Serva, A.; Sessa, F.; Lapi, A.; D’Angelo, P. Influence of Counterions on the Hydration Structure of Lanthanide Ions in Dilute Aqueous Solutions. J. Phys. Chem. B 2018, 122, 2779–2791. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Irmer, G. Hydration and ion pair formation in common aqueous La(III) salt solutions–a Raman scattering and DFT study. Dalton Trans. 2015, 44, 295–305. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Irmer, G. Raman spectroscopic characterization of light rare earth ions: La3+, Ce3+, Pr3+, Nd3+ and Sm3+ – hydration and ion pair formation. Dalton Trans. 2017, 46, 4235–4244. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Irmer, G. Hydration and ion pair formation in aqueous Y3+–salt solutions. Dalton Trans. 2015, 44, 18492–18505. [Google Scholar] [CrossRef]
- Friesen, S.; Krickl, S.; Luger, M.; Nazet, A.; Hefter, G.; Buchner, R. Hydration and ion association of La3+ and Eu3+ salts in aqueous solution. Phys. Chem. Chem. Phys. 2018, 20, 8812–8821. [Google Scholar] [CrossRef] [PubMed]
- Wood, S.A. The aqueous geochemistry of the rare-earth elements and yttrium. 1. Review of available low-temperature data for inorganic complexes and the inorganic REE speciation of natural waters. Chem. Geol. 1990, 82, 159–186. [Google Scholar] [CrossRef]
- Peppard, D.F.; Mason, G.W.; Hucher, I. Stability constants of certain lanthanide(III) and actinide(III) chloride and nitrate complexes. J. Inorg. Nucl. Chem. 1962, 24, 881–888. [Google Scholar] [CrossRef]
- Sekine, T. Complex formation of Lu(III), Eu(III), Lu(III) and Am(III) with oxalate, sulphate, chloride and thiocyanate ions. J. Inorg. Nucl. Chem. 1964, 26, 1463–1465. [Google Scholar] [CrossRef]
- Fukasawa, T.; Kawasuji, I.; Mitsugahiro, T.; Sat, A.; Suzuki, S. Investigation on the Complex Formation of Some Lanthanoids(III) and Actinoids(III) with chloride and Bromide. Bull. Chem. Soc. Japan 1982, 55, 726–729. [Google Scholar] [CrossRef]
- Choppin, G.R.; Unrein, P.J. Halide complexes of the lanthanide elements. J. Inorg. Nucl. Chem. 1963, 25, 387–393. [Google Scholar] [CrossRef]
- Irving, H.M.N.H.; Khopkar, P.K. The stability of the chloride complexes of europium. J. Inorg. Nucl. Chem. 1964, 26, 1561–1569. [Google Scholar] [CrossRef]
- Marcus, Y. Anion exchange of metal complexes—XV: Anion exchange and amine extraction of lanthanides and trivalent actinides from chloride solutions. J. Inorg. Nucl. Chem. 1966, 28, 209–219. [Google Scholar] [CrossRef]
- Breen, P.J.; Horrocks, W.D.W.J. Europium(III) luminescence excitation spectroscopy. Inner-sphere complexation of europium(III) by chloride, thiocyanate, and nitrate ions. Inorg. Chem. 1983, 22, 536–540. [Google Scholar] [CrossRef]
- Bünzli, J.C.G.; Yersin, J.R. Fluorescence spectra and lifetime measurements of aqueous solutions of europium nitrate and perchlorate. Inorg. Chem. 1979, 18, 605–607. [Google Scholar] [CrossRef]
- Gorbunov, A.O.; Lindqvist-Reis, P.; Mereshchenko, A.S.; Skripkin, M.Y. Solvation and complexation of europium(III) ions in triflate and chloride aqueous-organic solutions by TRLF spectroscopy. J. Mol. Liquids 2017, 240, 25–34. [Google Scholar] [CrossRef]
- Reuben, J.; Fiat, D. Nuclear Magnetic Resonance Studies of Solutions of the Rare-Earth Ions and Their Complexes. III. Oxygen-17 and Proton Shifts in Aqueous Solutions and the Nature of Aquo and Mixed Complexes. J. Chem. Phys. 1969, 51, 4909–4917. [Google Scholar] [CrossRef]
- Chen, Z.; Detellier, C. Interactions of La(III) with anions in aqueous solutions. A 139La NMR study. J. Sol. Chem. 1992, 21, 941–952. [Google Scholar] [CrossRef]
- Yaita, T.; Ito, D.; Tachimori, S. 139La NMR Relaxation and Chemical Shift Studies in the Aqueous Nitrate and Chloride Solutions. J. Phys. Chem. B 1998, 102, 3886–3891. [Google Scholar] [CrossRef]
- Purdie, N.; Vincent, C.A. Ultrasonic absorption in the lanthanide sulphates. Trans. Faraday Soc. 1967, 63, 2745–2757. [Google Scholar] [CrossRef]
- Fay, D.P.; Litchinsky, D.; Purdie, N. Ultrasonic absorption in aqueous salts of the lanthanides. J. Phys. Chem. 1969, 73, 544–552. [Google Scholar] [CrossRef]
- Garnsey, R.; Ebdon, D.W. Ionic association in aqueous lanthanide nitrate solutions by ultrasonic absorption spectroscopy. J. Am. Chem. Soc. 1969, 91, 50–56. [Google Scholar] [CrossRef]
- Voleišienė, B.; Rutkūnienė, D. Investigation of the hydration phenomenon in 3-1 electrolyte solutions. Ultragarsas 2007, 1, 45–47. [Google Scholar]
- Rudolph, W.W.; Mason, R.; Pye, C.C. Aluminium(III) hydration in aqueous solution. A Raman spectroscopic investigation and an ab initio molecular orbital study of aluminium(III) water clusters. Phys. Chem. Chem. Phys. 2000, 2, 5030–5040. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Irmer, G. Raman and Infrared Spectroscopic Investigations on Aqueous Alkali Metal Phosphate Solutions and Density Functional Theory Calculations of Phosphate—Water Clusters. Appl. Spectrosc. 2007, 61, 1312–1327. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Pye, C.C. Gallium(III) hydration in aqueous solution of perchlorate, nitrate and sulfate. Raman and 71-Ga NMR spectroscopic studies and ab initio molecular orbital calculations of gallium(III) water clusters. Phys. Chem. Chem. Phys. 2002, 4, 4319–4327. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Brooker, M.H.; Pye, C.C. Hydration of Lithium Ion in Aqueous Solutions. J. Phys. Chem. 1995, 99, 3793–3797. [Google Scholar] [CrossRef]
- Kanno, H. Hydrations of metal ions in aqueous electrolyte solutions: A Raman study. J. Phys. Chem. 1988, 92, 4232–4236. [Google Scholar] [CrossRef]
- Vogel, A.I. A Text-Book of Quantitative Inorganic Analysis, 3rd ed.; Longman: London, UK, 1961. [Google Scholar]
- Spedding, F.H.; Jaffe, S. Conductances, Solubilities and Ionization Constants of Some Rare Earth Sulfates in Aqueous Solutions at 25°. J. Am. Chem. Soc. 1954, 76, 882–884. [Google Scholar] [CrossRef]
- Rudolph, W.W.; Fischer, D.; Irmer, G. Vibrational Spectroscopic Studies and Density Functional Theory Calculations of Speciation in the CO2—Water System. Appl. Spectrosc. 2006, 60, 130–144. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A.J.T.; Vreven, K.N.; Kudin, J.C.; Burant, J.M.; et al. Gaussian 03, Revision, C.02; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.C. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Cossi, M.; Scalmani, G.; Rega, N.; Barone, V. New developments in the polarizable continuum model for quantum mechanical and classical calculations on molecules in solution. J. Chem. Phys. 2002, 117, 43–54. [Google Scholar] [CrossRef]
- Smith, D.W. Ionic hydration enthalpies. J. Chem. Educ. 1977, 54, 540–542. [Google Scholar] [CrossRef]
- Marcus, Y. A simple empirical model describing the thermodynamics of hydration of ions of widely varying charges, sizes, and shapes. Biophys. Chem. 1994, 51, 111–127. [Google Scholar] [CrossRef]
- Burgess, J. Ions in Solution: Basic Principles of Chemical Interactions; Ellis, H., Ed.; Chichester/Halsted Press: New York, NY, USA, 1988. [Google Scholar]
- Rudolph, W.; Schönherr, S. Raman- und Infrarotspektroskopische Untersuchungen an konzentrierten Aluminiumsalzlösungen. Z. Phys. Chem. 1989, 270, 1121–1134. [Google Scholar] [CrossRef]
- Pearson, R.G. Hard and Soft Acids and Bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
- Rao, L.; Tian, G. Complexation of Lanthanides with Nitrate at Variable Temperatures: Thermodynamics and Coordination Modes. Inorg. Chem. 2009, 48, 964–970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rudolph, W.W.; Irmer, G.; Hefter, G. Raman spectroscopic investigation of speciation in MgSO4(aq). Phys. Chem. Chem. Phys. 2003, 5, 5253–5261. [Google Scholar] [CrossRef]
- Klinkhammer, C.; Böhm, F.; Sharma, V.; Schwaab, G.; Seitz, M.; Havenith, M. Anion dependent ion pairing in concentrated ytterbium halide solutions. J. Chem. Phys. 2018, 148, 222802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Debye, P. Polare Molekeln; S. Hirzel-Verlag: Leipzig, Germany, 1929. [Google Scholar]
- Clark, A.E. Density Functional and Basis Set Dependence of Hydrated Ln(III) Properties. J. Chem. Theory Comput. 2008, 4, 708–718. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of Lu(ClO4)3(aq) and Lu(III)-triflate(cr) are available in small quantities from the authors. All other solutions have been used. |








| Bond Distances (Å) and Angels (°) | DFT Data/Gas Phase Cluster | DFT Data/Cluster + PC Model | ref. [25] | ref. [16] | ref. [24] | ref. [21] |
|---|---|---|---|---|---|---|
| Lu-O | 2.350 | 2.311 | 2.338 | 2.307 | 2.37 | 2.32 |
| O-H | 0.981 | 0.982 | - | - | - | - |
| H-O-H | 109.29 | 110.45 | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudolph, W.; Irmer, G. Hydration and Ion Pair Formation in Aqueous Lu3+- Solution. Molecules 2018, 23, 3237. https://doi.org/10.3390/molecules23123237
Rudolph W, Irmer G. Hydration and Ion Pair Formation in Aqueous Lu3+- Solution. Molecules. 2018; 23(12):3237. https://doi.org/10.3390/molecules23123237
Chicago/Turabian StyleRudolph, Wolfram, and Gert Irmer. 2018. "Hydration and Ion Pair Formation in Aqueous Lu3+- Solution" Molecules 23, no. 12: 3237. https://doi.org/10.3390/molecules23123237
APA StyleRudolph, W., & Irmer, G. (2018). Hydration and Ion Pair Formation in Aqueous Lu3+- Solution. Molecules, 23(12), 3237. https://doi.org/10.3390/molecules23123237