Topological Water Network Analysis Around Amino Acids
Abstract
:1. Introduction
2. Results and Discussion
2.1. Validation of MD Simulation Results for Each Amino Acid
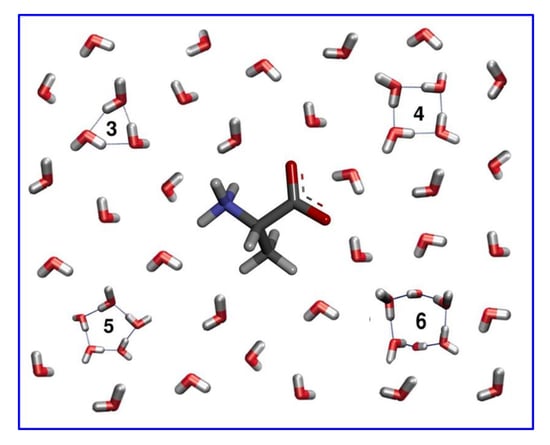
2.2. TWN Pattern Around Amino Acids
2.3. TWN Pattern for Residues of the PDB Structures
3. Materials and Methods
3.1. Preparation and Capping of Amino Acids
3.2. Molecular Dynamics (MD) Simulation
3.3. Topological Water Network (TWN) Analysis
3.4. Analysis of PDB Structures
3.4.1. Preparation of PDB Files
3.4.2. TWN Analysis of Filtered PDB Files
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bellissent-Funel, M.-C.; Hassanali, A.; Havenith, M.; Henchman, R.; Pohl, P.; Sterpone, F.; Van Der Spoel, D.; Xu, Y.; Garcia, A.E. Water determines the structure and dynamics of proteins. Chem. Rev. 2016, 116, 7673–7697. [Google Scholar] [CrossRef] [PubMed]
- Frey, M. Water structure associated with proteins and its role in crystallization. Acta Crystallogr. D 1994, 50, 663–666. [Google Scholar] [CrossRef] [PubMed]
- Ladbury, J.E. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 1996, 3, 973–980. [Google Scholar] [CrossRef] [Green Version]
- Poornima, C.; Dean, P. Hydration in drug design. 1. Multiple hydrogen-bonding features of water molecules in mediating protein-ligand interactions. J. Comput. Aided Mol. Des. 1995, 9, 500–512. [Google Scholar] [CrossRef] [PubMed]
- Hummer, G. Molecular binding: Under water’s influence. Nat. Chem. 2010, 2, 906. [Google Scholar] [CrossRef] [PubMed]
- Baron, R.; Setny, P.; McCammon, J.A. Water in cavity−ligand recognition. J. Am. Chem. Soc. 2010, 132, 12091–12097. [Google Scholar] [CrossRef] [PubMed]
- Baron, R.; Setny, P.; Paesani, F. Water structure, dynamics, and spectral signatures: Changes upon model cavity–Ligand recognition. J. Phys. Chem. B 2012, 116, 13774–13780. [Google Scholar] [CrossRef] [PubMed]
- Quiocho, F.; Wilson, D.K.; Vyas, N. Substrate specificity and affinity of a protein modulated by bound water molecules. Nature 1989, 340, 404. [Google Scholar] [CrossRef]
- Young, T.; Abel, R.; Kim, B.; Berne, B.J.; Friesner, R.A. Motifs for molecular recognition exploiting hydrophobic enclosure in protein–ligand binding. Proc. Natl. Acad. Sci. USA 2007, 104, 808–813. [Google Scholar] [CrossRef]
- Bayden, A.S.; Moustakas, D.T.; Joseph-McCarthy, D.; Lamb, M.L. Evaluating free energies of binding and conservation of crystallographic waters using SZMAP. J. Chem. Inf. Model. 2015, 55, 1552–1565. [Google Scholar] [CrossRef]
- Ramsey, S.; Nguyen, C.; Salomon-Ferrer, R.; Walker, R.C.; Gilson, M.K.; Kurtzman, T. Solvation thermodynamic mapping of molecular surfaces in AmberTools: GIST. J. Comput. Chem. 2016, 37, 2029–2037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ross, G.A.; Bodnarchuk, M.S.; Essex, J.W. Water sites, networks, and free energies with grand canonical Monte Carlo. J. Am. Chem. Soc. 2015, 137, 14930–14943. [Google Scholar] [CrossRef] [PubMed]
- Otto, K.E.; Xue, Z.; Zielke, P.; Suhm, M.A. The Raman spectrum of isolated water clusters. Phys. Chem. Chem. Phys. 2014, 16, 9849–9858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zischang, J.; Suhm, M.A. The OH stretching spectrum of warm water clusters. J. Chem. Phys. 2014, 140, 064312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richardson, J.O.; Pérez, C.; Lobsiger, S.; Reid, A.A.; Temelso, B.; Shields, G.C.; Kisiel, Z.; Wales, D.J.; Pate, B.H.; Althorpe, S.C. Concerted hydrogen-bond breaking by quantum tunneling in the water hexamer prism. Science 2016, 351, 1310–1313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buck, U.; Pradzynski, C.C.; Zeuch, T.; Dieterich, J.M.; Hartke, B. A size resolved investigation of large water clusters. Phys. Chem. Chem. Phys. 2014, 16, 6859–6871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, S.E.; Götz, A.W.; Cheng, X.; Steele, R.P.; Mandelshtam, V.A.; Paesani, F. Monitoring water clusters “melt” through vibrational spectroscopy. J. Am. Chem. Soc. 2017, 139, 7082–7088. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, M.; Baba, A.; Ohmine, I. Topological building blocks of hydrogen bond network in water. J. Chem. Phys. 2007, 127, 134504. [Google Scholar] [CrossRef] [PubMed]
- Cobar, E.A.; Horn, P.R.; Bergman, R.G.; Head-Gordon, M. Examination of the hydrogen-bonding networks in small water clusters (n = 2–5, 13, 17) using absolutely localized molecular orbital energy decomposition analysis. Phys. Chem. Chem. Phys. 2012, 14, 15328–15339. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, Y.; Kao, Y.-T.; Wang, L.; Zhong, D. Protein hydration dynamics and molecular mechanism of coupled water−protein fluctuations. J. Am. Chem. Soc. 2009, 131, 10677–10691. [Google Scholar] [CrossRef] [PubMed]
- Jung, D.H.; Yang, J.H.; Jhon, M.S. The effect of an external electric field on the structure of liquid water using molecular dynamics simulations. Chem. Phys. 1999, 244, 331–337. [Google Scholar] [CrossRef]
- Yu, J.Y.; Shin, J.K.; Jhon, M.S. The structure of water in human ras oncogene proteins. Int. J. Quantum Chem. 1994, 51, 241–254. [Google Scholar] [CrossRef]
- Rahaman, O.; Kalimeri, M.; Katava, M.; Paciaroni, A.; Sterpone, F. Configurational disorder of water hydrogen-bond network at the protein dynamical transition. J. Phys. Chem. B 2017, 121, 6792–6798. [Google Scholar] [CrossRef] [PubMed]
- Krimmer, S.G.; Cramer, J.; Betz, M.; Fridh, V.; Karlsson, R.; Heine, A.; Klebe, G. Rational design of thermodynamic and kinetic binding profiles by optimizing surface water networks coating protein-bound ligands. J. Med. Chem. 2016, 59, 10530–10548. [Google Scholar] [CrossRef] [PubMed]
- Jang, W.D.; Kim, J.-T.; Kang, N.S. The analysis of water network for kinase selectivity based on the MD simulations. J. Mol. Liq. 2014, 191, 37–41. [Google Scholar] [CrossRef]
- Jang, W.D.; Lee, M.H.; Kang, N.S. Quantitative assessment of kinase selectivity based the water-ring network in protein binding sites using molecular dynamics simulations. J. Mol. Liq. 2016, 221, 316–322. [Google Scholar] [CrossRef]
- Lee, M.; Balupuri, A.; Jung, Y.-R.; Choi, S.; Lee, A.; Cho, Y.; Kang, N.S. Design of a novel and selective IRAK4 inhibitor using topological water network analysis and molecular modeling approaches. Molecules 2018, 23, 3136. [Google Scholar] [CrossRef]
- Balupuri, A.; Choi, K.-E.; Kang, N.S. Computational insights into the role of α-strand/sheet in aggregation of α-synuclein. Sci. Rep. 2019, 9, 59. [Google Scholar] [CrossRef]
- Kyte, J.; Doolittle, R.F. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982, 157, 105–132. [Google Scholar] [CrossRef] [Green Version]
- Schauperl, M.; Podewitz, M.; Waldner, B.J.; Liedl, K.R. Enthalpic and entropic contributions to hydrophobicity. J. Chem. Theory Comput. 2016, 12, 4600–4610. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Vitalini, F.; Noé, F.; Keller, B.J. Molecular dynamics simulations data of the twenty encoded amino acids in different force fields. Data Brief. 2016, 7, 582–590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hovmöller, S.; Zhou, T.; Ohlson, T. Conformations of amino acids in proteins. Acta Crystallogr. D 2002, 58, 768–776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laage, D.; Elsaesser, T.; Hynes, J.T. Water dynamics in the hydration shells of biomolecules. Chem. Rev. 2017, 117, 10694–10725. [Google Scholar] [CrossRef] [PubMed]
- Kuntz, I., Jr.; Kauzmann, W. Hydration of proteins and polypeptides. Adv. Protein Chem. 1974, 28, 239–345. [Google Scholar]
- Bagchi, B. Water dynamics in the hydration layer around proteins and micelles. Chem. Rev. 2005, 105, 3197–3219. [Google Scholar] [CrossRef]
- Makarov, V.; Pettitt, B.M.; Feig, M. Solvation and hydration of proteins and nucleic acids: A theoretical view of simulation and experiment. Acc. Chem. Res. 2002, 35, 376–384. [Google Scholar] [CrossRef]
- Jeffrey, G.A. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997; p. 303. ISBN 0-19-509549-9. [Google Scholar]
- Nittinger, E.; Schneider, N.; Lange, G.; Rarey, M. Evidence of water molecules--a statistical evaluation of water molecules based on electron density. J. Chem. Inf. Model. 2015, 55, 771–783. [Google Scholar] [CrossRef]
- Dixon, D.A.; Lipscomb, W. Electronic structure and bonding of the amino acids containing first row atoms. J. Biol. Chem. 1976, 251, 5992–6000. [Google Scholar]
- Bjelkmar, P.; Larsson, P.; Cuendet, M.A.; Hess, B.; Lindahl, E. Implementation of the CHARMM force field in GROMACS: Analysis of protein stability effects from correction maps, virtual interaction sites, and water models. J. Chem. Theory Comput. 2010, 6, 459–466. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- RCSB PDB. Available online: http://ftp.rcsb.org (accessed on 3 February 2017).
- Carugo, O. When proteins are completely hydrated in crystals. Int. J. Biol. Macromol. 2016, 89, 137–143. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |





| (A) 3-ring TWNs (Backbone + Side chain) | |||||||||||||||||||||
| Ile | Val | Leu | Phe | Cys | Met | Ala | Gly | Thr | Trp | Ser | Tyr | Pro | Hsd | Hse | Gln | Asp | Asn | Glu | Lys | Arg | |
| O | 86 | 93 | 90 | 84 | 97 | 104 | 130 | 103 | 135 | 96 | 170 | 128 | 86 | 80 | 99 | 125 | 196 | 139 | 156 | 113 | 99 |
| N | 25 | 28 | 37 | 15 | 13 | 37 | 28 | 65 | 20 | 38 | 21 | 23 | 33 | 80 | 70 | 73 | 19 | 60 | 27 | 51 | 81 |
| C | 230 | 248 | 219 | 232 | 141 | 175 | 200 | 168 | 154 | 207 | 152 | 201 | 221 | 169 | 164 | 124 | 129 | 105 | 117 | 183 | 158 |
| S | 93 | 28 | |||||||||||||||||||
| Total | 341 | 369 | 346 | 331 | 344 | 344 | 358 | 336 | 309 | 341 | 343 | 352 | 340 | 329 | 333 | 322 | 344 | 304 | 300 | 347 | 338 |
| O,N/Total | 0.33 | 0.33 | 0.37 | 0.30 | 0.32 | 0.41 | 0.44 | 0.50 | 0.50 | 0.39 | 0.56 | 0.43 | 0.35 | 0.49 | 0.51 | 0.61 | 0.63 | 0.65 | 0.61 | 0.47 | 0.53 |
| C/Total | 0.67 | 0.67 | 0.63 | 0.70 | 0.41 | 0.51 | 0.56 | 0.50 | 0.50 | 0.61 | 0.44 | 0.57 | 0.65 | 0.51 | 0.49 | 0.39 | 0.37 | 0.35 | 0.39 | 0.52 | 0.47 |
| S/Total | 0.27 | 0.08 | |||||||||||||||||||
| (B) 3-ring TWNs (Backbone) | |||||||||||||||||||||
| Ile | Val | Leu | Phe | Cys | Met | Ala | Gly | Thr | Trp | Ser | Tyr | Pro | Hsd | Hse | Gln | Asp | Asn | Glu | Lys | Arg | |
| O | 86 | 93 | 90 | 84 | 97 | 104 | 130 | 103 | 91 | 96 | 95 | 109 | 86 | 80 | 99 | 87 | 88 | 97 | 79 | 113 | 99 |
| N | 25 | 28 | 37 | 15 | 13 | 37 | 28 | 65 | 20 | 18 | 21 | 23 | 33 | 24 | 27 | 20 | 19 | 22 | 27 | 28 | 24 |
| C | 111 | 115 | 105 | 111 | 118 | 104 | 125 | 168 | 106 | 112 | 123 | 111 | 91 | 105 | 97 | 106 | 106 | 89 | 104 | 119 | 122 |
| Total | 222 | 236 | 232 | 210 | 228 | 245 | 283 | 336 | 217 | 226 | 239 | 243 | 210 | 209 | 223 | 213 | 213 | 208 | 210 | 260 | 245 |
| O,N/Total | 0.50 | 0.51 | 0.55 | 0.47 | 0.48 | 0.58 | 0.56 | 0.50 | 0.51 | 0.50 | 0.49 | 0.54 | 0.57 | 0.50 | 0.57 | 0.50 | 0.50 | 0.57 | 0.50 | 0.54 | 0.50 |
| C/Total | 0.50 | 0.49 | 0.45 | 0.53 | 0.52 | 0.42 | 0.44 | 0.50 | 0.49 | 0.50 | 0.51 | 0.46 | 0.43 | 0.50 | 0.43 | 0.50 | 0.50 | 0.43 | 0.50 | 0.46 | 0.50 |
| (C) 3-ring TWNs (Side chain) | |||||||||||||||||||||
| Ile | Val | Leu | Phe | Cys | Met | Ala | Gly | Thr | Trp | Ser | Tyr | Pro | Hsd | Hse | Gln | Asp | Asn | Glu | Lys | Arg | |
| O | 44 | 75 | 19 | 38 | 108 | 42 | 77 | ||||||||||||||
| N | 20 | 56 | 43 | 53 | 38 | 23 | 57 | ||||||||||||||
| C | 119 | 133 | 114 | 121 | 23 | 71 | 75 | 48 | 95 | 29 | 90 | 130 | 64 | 67 | 18 | 23 | 16 | 13 | 64 | 36 | |
| S | 93 | 28 | |||||||||||||||||||
| Total | 119 | 133 | 114 | 121 | 116 | 99 | 75 | 92 | 115 | 104 | 109 | 130 | 120 | 110 | 109 | 131 | 96 | 90 | 87 | 93 | |
| O,N/Total | 0.48 | 0.17 | 0.72 | 0.17 | 0.47 | 0.39 | 0.83 | 0.82 | 0.83 | 0.86 | 0.26 | 0.61 | |||||||||
| C/Total | 1.00 | 1.00 | 1.00 | 1.00 | 0.20 | 0.72 | 1.00 | 0.52 | 0.83 | 0.28 | 0.83 | 1.00 | 0.53 | 0.61 | 0.17 | 0.18 | 0.17 | 0.14 | 0.74 | 0.39 | |
| S/Total | 0.80 | 0.28 | |||||||||||||||||||
| (A) 3-ring TWNs (Backbone + Side chain) | ||||||||||||||||||||
| Ile | Val | Leu | Phe | Cys | Met | Ala | Gly | Thr | Trp | Ser | Tyr | Pro | His | Gln | Asp | Asn | Glu | Lys | Arg | |
| O | 3514 | 5045 | 6504 | 3003 | 918 | 1260 | 7254 | 8653 | 13110 | 1237 | 14400 | 8618 | 5832 | 1853 | 8862 | 29681 | 10018 | 28546 | 5174 | 4405 |
| N | 377 | 698 | 925 | 453 | 133 | 265 | 1259 | 1912 | 631 | 656 | 904 | 357 | 92 | 3733 | 3708 | 1305 | 4531 | 1038 | 8825 | 10522 |
| C | 591 | 813 | 980 | 578 | 33 | 338 | 1035 | 590 | 924 | 345 | 418 | 501 | 1627 | 785 | 450 | 351 | 329 | 776 | 1505 | 882 |
| S | 146 | 107 | ||||||||||||||||||
| Total | 4482 | 6556 | 8409 | 4034 | 1230 | 1970 | 9548 | 11155 | 14665 | 2238 | 15722 | 9476 | 7551 | 6371 | 13020 | 31337 | 14878 | 30360 | 15504 | 15809 |
| O,N/Total | 0.87 | 0.88 | 0.88 | 0.86 | 0.85 | 0.77 | 0.89 | 0.95 | 0.94 | 0.85 | 0.97 | 0.95 | 0.78 | 0.88 | 0.97 | 0.99 | 0.98 | 0.97 | 0.90 | 0.94 |
| C/Total | 0.13 | 0.12 | 0.12 | 0.14 | 0.03 | 0.17 | 0.11 | 0.05 | 0.06 | 0.15 | 0.03 | 0.05 | 0.22 | 0.12 | 0.03 | 0.01 | 0.02 | 0.03 | 0.10 | 0.06 |
| S/Total | 0.12 | 0.05 | ||||||||||||||||||
| (B) 3-ring TWNs (Backbone) | ||||||||||||||||||||
| Ile | Val | Leu | Phe | Cys | Met | Ala | Gly | Thr | Trp | Ser | Tyr | Pro | His | Gln | Asp | Asn | Glu | Lys | Arg | |
| O | 3514 | 5045 | 6504 | 3003 | 918 | 1260 | 7254 | 8653 | 4959 | 1237 | 5402 | 2765 | 5832 | 1853 | 3062 | 5656 | 3866 | 5005 | 5174 | 4405 |
| N | 377 | 698 | 925 | 453 | 133 | 265 | 1259 | 1912 | 631 | 141 | 904 | 357 | 92 | 298 | 572 | 1305 | 882 | 1038 | 883 | 625 |
| C | 13 | 25 | 38 | 18 | 6 | 13 | 176 | 590 | 42 | 10 | 88 | 22 | 95 | 38 | 38 | 61 | 56 | 62 | 52 | 68 |
| Total | 3904 | 5768 | 7467 | 3474 | 1057 | 1538 | 8689 | 11155 | 5632 | 1388 | 6394 | 3144 | 6019 | 2189 | 3672 | 7022 | 4804 | 6105 | 6109 | 5098 |
| O,N/Total | 1.00 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.95 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| C/Total | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.05 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| (C) 3-ring TWNs (Side chain) | ||||||||||||||||||||
| Ile | Val | Leu | Phe | Cys | Met | Ala | Gly | Thr | Trp | Ser | Tyr | Pro | His | Gln | Asp | Asn | Glu | Lys | Arg | |
| O | 8151 | 8998 | 5853 | 5800 | 24025 | 6152 | 23541 | |||||||||||||
| N | 515 | 3435 | 3136 | 3649 | 7942 | 9897 | ||||||||||||||
| C | 578 | 788 | 942 | 560 | 27 | 325 | 859 | 882 | 335 | 330 | 479 | 1532 | 747 | 412 | 290 | 273 | 714 | 1453 | 814 | |
| S | 146 | 107 | ||||||||||||||||||
| Total | 578 | 788 | 942 | 560 | 173 | 432 | 859 | 9033 | 850 | 9328 | 6332 | 1532 | 4182 | 9348 | 24315 | 10074 | 24255 | 9395 | 10711 | |
| O,N/Total | 0.90 | 0.61 | 0.96 | 0.92 | 0.82 | 0.96 | 0.99 | 0.97 | 0.97 | 0.85 | 0.92 | |||||||||
| C/Total | 1.00 | 1.00 | 1.00 | 1.00 | 0.16 | 0.75 | 1.00 | 0.10 | 0.39 | 0.04 | 0.08 | 1.00 | 0.18 | 0.04 | 0.01 | 0.03 | 0.03 | 0.15 | 0.08 | |
| S/Total | 0.84 | 0.25 | ||||||||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, K.-E.; Chae, E.; Balupuri, A.; Yoon, H.R.; Kang, N.S. Topological Water Network Analysis Around Amino Acids. Molecules 2019, 24, 2653. https://doi.org/10.3390/molecules24142653
Choi K-E, Chae E, Balupuri A, Yoon HR, Kang NS. Topological Water Network Analysis Around Amino Acids. Molecules. 2019; 24(14):2653. https://doi.org/10.3390/molecules24142653
Chicago/Turabian StyleChoi, Kwang-Eun, Eunkyoung Chae, Anand Balupuri, Hye Ree Yoon, and Nam Sook Kang. 2019. "Topological Water Network Analysis Around Amino Acids" Molecules 24, no. 14: 2653. https://doi.org/10.3390/molecules24142653
APA StyleChoi, K. -E., Chae, E., Balupuri, A., Yoon, H. R., & Kang, N. S. (2019). Topological Water Network Analysis Around Amino Acids. Molecules, 24(14), 2653. https://doi.org/10.3390/molecules24142653