Next Article in Journal
Peptides: Prospects for Use in the Treatment of COVID-19
Next Article in Special Issue
Design and Synthesis of a Chiral Halogen-Bond Donor with a Sp3-Hybridized Carbon–Iodine Moiety in a Chiral Fluorobissulfonyl Scaffold
Previous Article in Journal
Resonance Raman Optical Activity Spectroscopy in Probing Structural Changes Invisible to Circular Dichroism Spectroscopy: A Study on Truncated Vitamin B12 Derivatives
Previous Article in Special Issue
Design and Evaluation of Anti-SARS-Coronavirus Agents Based on Molecular Interactions with the Viral Protease
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 25
Issue 19
10.3390/molecules25194388
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

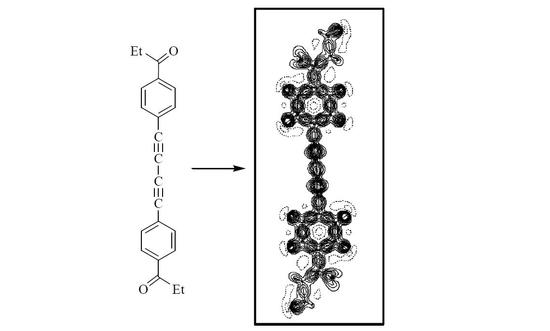
Is It Conjugated or Not? The Theoretical and Experimental Electron Density Map of Bonding in p-CH3CH2COC6H4-C≡C-C≡C-p-C6H4COCH3CH2

by
Przemysław Starynowicz
,
Sławomir Berski
,
Nurbey Gulia
,
Karolina Osowska
,
Tadeusz Lis
and
Sławomir Szafert
*
Department of Chemistry, University of Wrocław, 14 F. Joliot-Curie, 50-383 Wrocław, Poland
*
Author to whom correspondence should be addressed.
Molecules 2020, 25(19), 4388; https://doi.org/10.3390/molecules25194388
Submission received: 15 July 2020 / Revised: 19 September 2020 / Accepted: 19 September 2020 / Published: 24 September 2020
(This article belongs to the Special Issue Feature Papers to Celebrate Molecules Reaches 20,000 Articles Milestone)
Browse Figures
Review Reports Versions Notes

Abstract

:
The electron density of p-CH3CH2COC6H4-C≡CC≡C-p-C6H4COCH3CH2 has been investigated on the basis of single-crystal X-ray diffraction data collected to high resolution at 100 K and from theoretical calculations. An analysis of the X-ray data of the diyne showed interesting “liquidity” of electron distribution along the carbon chain compared to 1,2-diphenylacetylene. These findings are compatible with the results of topological analysis of Electron Localization Function (ELF), which has also revealed a larger (than expected) concentration of the electron density at the single bonds. Both methods indicate a clear π-type or “banana” character of a single bond and a significant distortion from the typical conjugated structure of the bonding in the diyne with a small contribution of cumulenic structures.

Graphical Abstract

1. Introduction

Within the last three decades, research on organic, organometallic and metal-containing polyynes has focused a lot of attention and witnessed a series of stunning breakthroughs [1,2]. Such compounds of rigid-rod architecture are envisioned as precursors of still elusive sp-hybridized carbon allotrope—carbyne. Yet another important factor that significantly spurred the research in this area is the extraordinary (and somehow surprising) physical properties of such “material” that have been predicted by theorists. They suggest (based on theoretical calculations) that carbyne possesses for instance, a tensile strength that surpasses that of carbon nanotubes, graphene, and diamond [3,4,5].
In order to better understand the physical and chemical properties of polyynes and gain a deeper insight into the detailed electronic structure of a carbon chain, various series of oligo and polyynes of type X(C≡C)nX have been synthesized and thoroughly studied [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. The received data allowed to define the effect of a chain length upon various molecular properties and quantify a dependence of many measurable physical values, like an absorption band, redox potential, or NMR chemical shifts against 1/n (where n is the number of alkyne units).
The structure of the polyyne chain itself is of great interest from several standpoints. One of the most intriguing questions is: With the chain lengthening, will the triple and single bond equalize (a vanishing HOMO/LUMO energy gap) or approach two different values (a persistent energy gap; from a solid-state physics perspective, a Peierls distortion) [27,28]? Another good question is: To what degree carbyne can easily bend? There has been conjecture that distortion of long sp carbon chains might trigger isomerization to fullerenes or other sp2 carbon allotropes [29,30,31,32,33,34,35].
In the 2003 review article (followed by the 2006 update paper), all crystallographically characterized compounds with at least eight consecutive sp hybridized carbons (four conjugated C≡C bonds) were analyzed [36]. The major interest—at the molecular level—were bond lengths, bond angles, and sp carbon chain conformations. Average values derived from bond length suggested that (1) as the midpoints of the sp carbon chains are approached, the C-C bonds contract and the C≡C bonds lengthen, and (2) as the chains are extended to the macromolecular limit of the one-dimensional carbon allotrope (carbyne), the C-C bonds contract to the proposed limiting value 1.32–1.33 Å and the C≡C bonds lengthen to 1.25 Å (the effect of the error limits on the bond lengths (esd values) is omitted).
Although in further approximations of these limits, computational chemists will still play a crucial role we believe some additional important experimental values can be gathered. This would of course, include precise crystallographic electron density maps of bonding in polyynes. Although, what is obvious, the main interest should be directed at longer polyynes as an initial point we present here the map of a diyne with a carbonyl group containing phenyl endgroups, which is next compared with a theoretical one.

2. Results and Discussion

The experimental difficulties of the research on electron density maps are worth mentioning. First, the highest quality crystals are required. Second, the compound and its crystals must be extremely stable and should not change (cracking, phase transitions, etc.) during an experiment. Third, there must not be any disorder in the measured crystal and data must be collected and processed with the utmost care. Long-lasting optimization of the crystallization process (speed, temperature, concentration) and pure luck allowed us to finally obtain crystals of sufficiently good quality to constitute a proper data source for such an experiment. The crystal structure was first solved conventionally and the results have already been published [37].
The diyne p-CH3CH2COC6H4-C≡CC≡C-p-C6H4COCH3CH2 (1) was synthesized as described earlier and it was fully characterized including 1H- and 13C-NMR and IR spectroscopy, MS spectrometry and X-ray crystallography [37]. Next, data for the carefully selected crystal were collected as described in the Experimental Section. The view of the structure is presented in Figure 1 and the metrical parameters from conventional (CR) and multipole (MP) refinement are compared in Table 1.
As it can easily be noticed, the inclusion of the multipole parameters has led to just subtle modifications of the bond lengths. The distribution of the electric charge is given in Table 2 and the multipole deformation density is presented in Figure 2a. The final residue density map as shown in Figure 2b was essentially featureless with ρres between −0.1 and 0.2 e/Å3.
The negative charge of the carbonyl O(1) atom of −0.59(5) is similar to those in strychnine (−0.49(7)) [38] and 3-acetylcoumarin (−0.51 and −0.58) [39]. The benzene ring as a whole is slightly positive, with the sum charge of 0.53. Similarly, there is also a deficit of electrons on the terminal ethyl group, with its total charge of 0.56. The anomalously high negative charge of H(52) (−0.28(9)) results probably from imperfect partitioning of the electron density between this atom and C(5). The same can be observed for the C(16)-H(16) pair. The excess of the electron density is accumulated on the two carbon atoms (within the symmetry independent half of the molecule) involved in the triple bonds—the sum of their monopole charges is −0.55.
The essential topological parameters of the charge distribution are summarized in Table 3.
The parameters for the triple bond C(1)-C(2), density in the bond critical point (ρcp) and the value of Laplacian (Δρcp), are somewhat larger than those reported for two crystallographically independent molecules of 1,2-diphenylacetylene (ρcp = 2.79 eÅ−3 for both, Δρcp = −21.0 and −20.8 eÅ−5) [40]. The values obtained for the present molecule are close to those for the ideal triple bond −2.82 eÅ−3 and −30.9 eÅ−5 [41].
Contrary to 1,2-diphenylacetylene molecules the ellipticity, ε (defined as λ1/λ2 − 1, where λ1 and λ2 are the negative values of the ∂2ρcp/∂xi∂xj matrix) of the C(1)-C(2) bond is very low (0.02; 0.25 and 0.20 for 1,2-diphenylacetylene) and the perpendicular bond section is practically circular.
In the case of the aromatic ring ρcp with values, 2.12–2.21 eÅ−3 (av. 2.18 eÅ−3) resembles the one reported in 1,2-diphenylacetylene, whereas Δρcp, in the range from −18.8 to −20.2 eÅ−5 (av. −19.5 eÅ−5) is slightly smaller than for the cited molecule (from −16.4 to −17.1 eÅ−5). The average ellipticity of the aromatic C-C bonds is 0.13, definitely smaller than for benzene molecule (0.23) and slightly smaller than in 1,2-diphenylacetylene [42]. The presented data indicate the charge migration from the aromatic rings to the triple bond, contrary to what was observed in the cited molecule.
The density in the critical point of the C(3)-O(1) carbonyl bond is similar to the density of carbonyl bond in other compounds (where this group is not a part of the peptide bond), e.g., 2.69(3) eÅ−3 in 1-(4-fluorophenyl)-3,6,6-trimethyl-2-phenyl-1,5,6,7-tetrahydro-4H-indol-4-one [43] or 2.856 eÅ−3 in estrone [44]. On the other hand the Laplacian value of −6.3 eÅ−5 is significantly higher than in these two compounds, where Δρcp was −24.38(7) and −17.56 eÅ−5, respectively. Rather surprisingly, the ellipticity of this bond of 0.04 is small as compared to what might be expected for a double bond. Nevertheless, this value is similar to the ellipticity of the carbonyl bond in estrone (0.05; for 1-(4-fluorophenyl)-3,6,6-trimethyl-2-phenyl-1,5,6,7-tetrahydro-4H-indol-4-one it was 0.28). As far as the single bonds C(5)-C(4), C(4)-C(3) and C(3)-C(14) are concerned, it may be noticed that ρcp mildly increases and Δρcp decreases. The latter is accompanied by moderate growth of ellipticity: 0.02, 0.04 and 0.08 for C(5)-C(4), C(4)-C(3) and C(3)-C(14), respectively. The parameters for the formally single bonds C(11)-C(1) and C(2)-C(2A) indicate that their character is close to aromatic, with the exception of small ellipticity of 0.05 and 0.04, respectively.
The simulation of the electronic properties of the crystal of 1 was performed next. Calculations for the experimental geometry yielded the lattice energy (Ecryst), which strongly depends on the electron density functional chosen, as shown in Table 4. The Ecryst ranges from −100.7 kcal/mol (SVWN) to −28.2 kcal/mol (B3PW). After correction for BSSE effects in the counterpoise correction scheme [45] Ecryst has been reduced to −78.3 kcal/mol (SVWN) and −8.4 kcal/mol (B3PW). For further analysis, only the results achieved with the hybrid electron density functional B3LYP [46,47,48] were adopted (Ecryst = −54.9, Ecryst + BSSE = −32.3 kcal/mol), which are commonly used in studies on non-interacting molecules.
The electron density distribution calculated for the R-(C11)-C(1)-C(2)-C(2A)-C(1A)-(C11A)-R fragment (R = p-C6H4COC2H5) at the molecular plane is presented in Figure 3. One can distinguish a large concentration of the electron density in the region of C(1)-C(2) and C(1A)-C(2A) bonds (slightly smaller for the C(2)-C(2A)) and relatively small concentration in the area of the C(11)-C(1) and C(11A)-C(1A) bonds. The largest amount of electrons is observed outside the interatomic axis. Interestingly, the electron distribution in the C(1)-C(2) and C(1A)-C(2A) regions resembles a picture of two pairs of “banana” bonds, as previously suggested by Pauling for the double bond in ethylene [49]. Adopting the π-σ representation, one would postulate an essential π-type character for the C(1)-C(2), C(1A)-C(2A) and C(2)-C(2A) bonds. On this basis, it seems reasonable to represent the bonding in the carbon chain (simplified manner) with the R–C≡C–C≡C–R formula but Lewis structures containing the double C(2)=C(2A) bond should also be taken into account.
To study the nature of the chemical bonds in the C(11)-C(1)-C(2)-C(2A)-C(1A)-C(11A) atomic chain a topological analysis of the electron localization function (ELF) was carried out for the isolated molecule as outlined in the experimental section (theoretical calculations section). The ELF function was introduced by Becke and Edgecombe [50] as a “simple measure of electron localization in atomic and molecular systems”. Figure 4 presents the 3D plot of the ELF function with marked basin populations.
For each pair of atoms in the carbon chain, disynaptic bonding basins were observed: V(C11,C1), V(C1,C2), V(C2,C2A), V(C2A,C1A), V(C1A,C11A). The largest basins are found for the C(1)-C(2) and C(1A)-C(2A) bonds with a torus-like shape being in agreement with the observation of large electron concentration outside the interatomic axis. Each of the V(C1,C2), V(C2A,C1A) basins are associated with two attractors (local maxima) of ELF and it suggests multiple types of carbon-carbon bonding. In the case of the V(C11,C1), V(C1A,C11A) and V(C2,C2A) basins, only single attractors are localized, usually corresponding to single bonds. However, one has to remember that there is no clear correlation between a number of bonding attractors and bond multiplicity. As one could expect, the largest basin population ( N ¯ ) of 5.17 e is computed for the V(C1,C2) and V(C2A,C1A) basins, which is very similar to 5.13 e calculated previously for the isolated HC≡CH molecule [51]. Such a large value of N ¯ characterizes the depleted triple bond and agrees with formal representation with R-C≡C-C≡C-R Lewis structure. The central C(2)-C(2A) bond having 2.74 e is more saturated by the electron density than the C(11-C1), C(11A)-C(1A) bonds with 2.46 e and from a topological point of view, it can be described as intermediate between double and single bonds. On this basis, an additional representation of the bonding may be proposed, which contains a cumulene chain of the carbon atoms. It is worth to notice, that shorter carbon-carbon bond corresponds to larger value of the basin population, for instance, r(C(11)-C(1)) > r(C(2)-C(2A)) > r(C(1)-C(2)) and respective basin populations: 2.46 e < 2.74 e < 5.13 e.
A “bridge” between the mathematical theory of the chemical bond contained in topological analysis of the ELF function (with non-integer values of the basin populations) and “classical view” where the chemical bond is formed through the sharing of electron pair(s) may be derived from a resonance of the Lewis structures. In Figure 5, five resonance forms are presented with corresponding percentages of occurrence in the mesomeric equilibrium.
The largest contribution has been computed for the structure I (54%), which corresponds to the R-C≡C-C≡C-R Lewis structure with an alternating triple (C(1)≡C(2), C(1A)≡C(2A)) and single (C(11)-C(1), C(2)-C(2A), C(1A)-C(11A)) bonds. In this structure, no formal charge is given to any atom (preferable form) and it reflects the large basin population (5.17 e) calculated for the V(C1,C2), V(C2A,C1A) basins. The Lewis structures II and III (symmetric forms) participate with 19% percentages to the equilibrium and reflect cumulene ((+)R=C=C=C=C(−)-R ↔ R-(−)C=C=C=C=R(+)) character of the bonding. Both resonance forms have formal charges −1, +1 at the C(1) and R and introduce a charge separation due to delocalization. Furthermore, they are responsible for the rigidity of the carbon chain and smaller than 6.0 e population between acetylenic carbons C(1) and C(2) but increase on the C(11)-C(1) and C(2)-C(2A) bonds. The Lewis structures IV and V (symmetric forms) represent the mixed cumulene-acetylenic character of the bonding. Both forms participate with a very small contribution of 4% to the resonance equilibrium. Comparing only contributions of the Lewis structures I to III, one can conclude that the bonding in the carbon chain possesses 1.42 times larger acetylenic than cumulene character. Furthermore, an approximate percentage ratio of three types of the Lewis structures (I:II, III:IV, V) may be simplified as 7:5:1.

3. Experimental Section

X-ray diffraction data were collected by using a KUMA KM4 CCD (ω scan technique, Kuma Diffraction, Wroclaw, Poland) diffractometer equipped with an Oxford Cryosystem cryostream cooler. Crystals of 1 suitable for an X-ray diffraction experiment were grown at room temperature (25 °C) from a CH2Cl2 solution gently layered on top with hexanes. The crystal selected for the measurement was picked directly from a mother liquor and immediately transferred to a diffractometer where it was cooled to 100 K.

3.1. Multipole Refinement

The multipole refinement was performed against 6073 merged reflections with I ≥ 3σ (I) with XD suite of programs [52], using the coordinates obtained from the conventional refinement. The C-H distances were fixed at 1.083 Å, in agreement with the typical values obtained from neutron diffraction data. The multipole formalism was described by Hansen and Coppens [53]. The multipoles were expanded up to octupoles for the C and O, and up to quadrupoles for H. The κ and κ’ parameters (separately for C and O atoms) were refined, whereas those for H were kept fixed at 1.2 (attempts to relax them failed). The topological analysis of the experimental charge density distribution was performed with XDPROP routine of the XD package following the ideas set out by Bader [54].

3.2. Theoretical Calculations

A simulation of electronic properties of the crystal has been performed for experimental geometry by means of the periodic ab initio DFT calculations using the CRYSTAL03 program [55]. Different combinations of the exchange and correlation functionals: SVWN, PWGGA, B3LYP and B3PW in conjunction with the 6-31G(d,p) basis set were employed [56,57]. A topological analysis of the electron localization function (ELF) [50] was carried out for the isolated molecule by means of the DGrid 4.2/Basin 4.2. programs [58,59]. Molecular orbitals have been generated for the crystal geometry at the B3LYP/6-311++G(d,p) computational level using Gaussian03 program [58,59,60,61,62]. The 3D plot of the ELF function was obtained by means of the Molekel program [63].

4. Conclusions

In conclusion, we have presented the first example of the experimental electron density map of the conjugated diyne p-CH3CH2COC6H4-C≡C-C≡C-p-C6H4COCH3CH2. The results clearly showed, that electrons in this arene-acetylene system are quite liquid. Compared to the results obtained for 1,2-diphenylacetylene, our data unambiguously indicated that insertion of an additional triple bond and concomitant conjugation in the -C≡C-C≡C- system remarkably change the charge distribution. This is due to the fact that conjugated triple bonds in 1 attract charge from the aromatic rings, contrary to the single -C≡C- bond in 1,2-diphenylacetylene. This experimental finding has been supported by theoretical studies on the chemical bonding in 1 performed with the use of topological analysis of the ELF function. Also, this method showed the bonding not to be a simply alternating single-triple-single-triple-single system, but revealed an enhancement of the electron density at the single bonds. This was to the extent that these bonds may be regarded as intermediates between the single and the double bonds.

Author Contributions

Conceptualization, S.S.; density map by multipole refinement, P.S.; experimental methodology and crystallization, K.O. and N.G.; data collection and crystal structure solution, T.L.; theoretical methodology, S.B. All authors have read and agreed to the published version of the manuscript.

Funding

We thank the Polish State Committee for Scientific Research (grant N204 140 31/3236) for support of this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cataldo, F. Polyynes. Synthesis, Properties and Applications; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
  2. Chalifoux, W.A.; Tykwinski, R.R. Synthesis of extended polyynes: Toward carbyne. Comptes Rendus Chim. 2009, 12, 341–358. [Google Scholar] [CrossRef]
  3. Banhart, F. Chains of carbon atoms: A vision or a new nanomaterial? Beilstein J. Nanotechnol. 2015, 6, 559–569. [Google Scholar] [CrossRef] [Green Version]
  4. Liu, M.; Artyukhov, V.I.; Lee, H.; Xu, F.; Yakobson, B.I. Carbyne from First Principles: Chain of C Atoms, a Nanorod or a Nanorope. ACS Nano 2013, 7, 10075–10082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Timoshevskii, A.; Kotrechko, S.; Matviychuk, Y. Atomic structure and mechanical properties of carbyne. Phys. Rev. B Condens. Matter 2015, 91, 245434. [Google Scholar] [CrossRef] [Green Version]
  6. Mohr, W.; Stahl, J.; Hampel, F.; Gladysz, J.A. Synthesis, Structure, and Reactivity of sp Carbon Chains with Bis(phosphine)Pentafluorophenylplatinum Endgroups: Butadiynediyl (C4) through Hexadecaoctaynediyl (C16) Bridges, and Beyond. Chem. Eur. J. 2003, 9, 3324–3340. [Google Scholar] [CrossRef] [PubMed]
  7. Chalifoux, W.A.; McDonald, R.; Ferguson, M.J.; Tykwinski, R.R. tert-Butyl-End-Capped Polyynes: Crystallographic Evidence of Reduced Bond-Length Alternation. Angew. Chem. Int. Ed. 2009, 48, 7915–7919. [Google Scholar] [CrossRef]
  8. Eisler, S.; Slepkov, A.D.; Elliot, E.; Luu, T.; McDonald, R.; Hegmann, F.A.; Tykwinski, R.R. Polyynes as a Model for Carbyne: Synthesis, Physical Properties, and Nonlinear Optical Response. J. Am. Chem. Soc. 2005, 127, 2666–2676. [Google Scholar] [CrossRef]
  9. Gibtner, T.; Hampel, F.; Gisselbrecht, J.-P.; Hirsch, A. End-Cap Stabilized Oligoynes: Model Compounds for the Linear sp Carbon Allotrope-Carbyne. Chem. Eur. J. 2002, 8, 408–432. [Google Scholar] [CrossRef]
  10. Zheng, Q.; Gladysz, J.A. A Synthetic Breakthrough into an Unanticipated Stability Regime: Readily Isolable Complexes in which C16-C28 Polyynediyl Chains Span Two Platinum Atoms. J. Am. Chem. Soc. 2005, 127, 10508–10509. [Google Scholar] [CrossRef]
  11. Bruce, M.I.; Zaitseva, N.N.; Nicholson, B.K.; Skelton, B.W.; White, A.H. Syntheses and molecular structures of some compounds containing many-atom chains end-capped by tricobalt carbonyl clusters. J. Organomet. Chem. 2008, 693, 2887–2897. [Google Scholar] [CrossRef]
  12. Dembinski, R.; Bartik, T.; Bartik, B.; Jaeger, M.; Gladysz, J.A. Toward Metal-Capped One-Dimensional Carbon Allotropes: Wirelike C6-C20 Polyynediyl Chains That Span Two Redox-Active (η5-C5Me5)Re(NO)(PPh3) Endgroups. J. Am. Chem. Soc. 2000, 122, 810–822. [Google Scholar] [CrossRef]
  13. Chalifoux, W.A.; Tykwinski, R.R. Synthesis of polyynes to model the sp-carbon allotrope carbyne. Nat. Chem. 2010, 2, 967–971. [Google Scholar] [CrossRef] [PubMed]
  14. Cao, Z.; Xi, B.; Jodoin, D.S.; Zhang, L.; Cummings, S.P.; Gao, Y.; Tyler, S.F.; Fanwick, P.E.; Crutchley, R.J.; Ren, T. Diruthenium-Polyyn-diyl-Diruthenium Wires: Electronic Coupling in the Long Distance Regime. J. Am. Chem. Soc. 2014, 136, 12174–12183. [Google Scholar] [CrossRef] [PubMed]
  15. Schermann, G.; Grösser, T.; Hampel, F.; Hirsch, A. Dicyanopolyynes: A Homologuous Series of End-Capped Linear sp Carbon. Chem. Eur. J. 1997, 3, 1105–1112. [Google Scholar] [CrossRef]
  16. Luu, T.; Elliot, E.; Slepkov, A.D.; Eisler, S.; McDonald, R.; Hegmann, F.A.; Tykwinski, R.R. Synthesis, Structure, and Nonlinear Optical Properties of Diarylpolyynes. Org. Lett. 2005, 7, 51–54. [Google Scholar] [CrossRef]
  17. Werz, D.B.; Gleiter, R.; Rominger, F. Tellurium-capped carbon rods: Syntheses and electronic and structural properties. Organometallics 2003, 22, 843–849. [Google Scholar] [CrossRef]
  18. Werz, D.B.; Gleiter, R. Polyalkynes capped by sulfur and selenium. J. Org. Chem. 2003, 68, 9400–9405. [Google Scholar] [CrossRef]
  19. Coat, F.; Paul, F.; Lapinte, C.; Toupet, L.; Costuas, K.; Halet, J.-F. Chemistry of the 1,3,5,7-octatetraynediyl carbon rod end-capped by two electron-rich (η5-C5Me5)(η2-dppe) Fe groups. J. Organomet. Chem. 2003, 683, 368–378. [Google Scholar] [CrossRef]
  20. Xu, G.-L.; Zou, G.; Ni, Y.-H.; DeRosa, M.C.; Crutchley, R.J.; Ren, T. Polyyn-diyls capped by diruthenium termini: A new family of carbon-rich organometallic compounds and distance-dependent electronic coupling therein. J. Am. Chem. Soc. 2003, 125, 10057–10065. [Google Scholar] [CrossRef]
  21. Weisbach, N.; Kuhn, H.; Amini, H.; Ehnbom, A.; Hampel, F.; Reibenspies, J.H.; Hall, M.B.; Gladysz, J.A. Triisopropylsilyl (TIPS) Alkynes as Building Blocks for Syntheses of Platinum Triisopropylsilylpolyynyl and Diplatinum Polyynediyl Complexes. Organometallics 2019, 38, 3294–3310. [Google Scholar] [CrossRef]
  22. Yam, V.W.-Y.; Wong, K.M.-C.; Zhu, N. Luminescent Platinum(II) Terpyridyl-Capped Carbon-Rich Molecular Rods—An Extension from Molecular- to Nanometer-Scale Dimensions. Angew. Chem. Int. Ed. 2003, 42, 1400–1403. [Google Scholar] [CrossRef] [PubMed]
  23. Sakurai, A.; Akita, M.; Moro-oka, Y. Synthesis and Characterization of the Dodecahexaynediyldiiron Complex, Fp*−(C≡C)6−Fp* [Fp*= Fe(η5-C5Me5)(CO)2], the Longest Structurally Characterized Polyynediyl Complex. Organometallics 1999, 18, 3241–3244. [Google Scholar] [CrossRef]
  24. Classen, J.; Gleiter, R.; Rominger, F. Oligoalkyne-Bridged (η4-Cyclobutadiene)(η5-cyclopentadienyl)cobalt Fragments—Syntheses and Properties. Eur. J. Inorg. Chem. 2002, 2002, 2040–2046. [Google Scholar] [CrossRef]
  25. Adams, R.D.; Qu, B.; Smith, M.D. Synthesis and characterization of 1,12-Bis (ferrocenyl)-1,3,5,7,9,11-dodecahexayne and its coordination to triosmium and dicobalt carbonyls. Organometallics 2002, 21, 3867–3872. [Google Scholar] [CrossRef]
  26. Antonova, A.B.; Bruce, M.I.; Ellis, B.G.; Gaudio, M.; Humphrey, P.A.; Jevric, M.; Melino, G.; Nicholson, B.K.; Perkins, G.J.; Skelton, B.W.; et al. A novel methodology for the synthesis of complexes containing long carbon chains linking metal centres: Molecular structures of {Ru(dppe)Cp*}2(μ-C14) and {Co3(μ-dppm)(CO)7}2(μ3:μ3-C16). Chem. Commun. 2004, 8, 960–961. [Google Scholar] [CrossRef] [PubMed]
  27. Kennedy, T.; Lieb, E.H. Proof of the Peierls Instability in One Dimension. Phys. Rev. Lett. 1987, 59, 1309–1312. [Google Scholar] [CrossRef] [PubMed]
  28. Khanna, S.K.; Pouget, J.P.; Comes, R.; Garito, A.F.; Heeger, A. X-ray studies of 2kF and 4kF anomalies in tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. B 1977, 16, 1468–1479. [Google Scholar] [CrossRef]
  29. Hunter, J.M.; Fye, J.L.; Roskamp, E.J.; Jarrold, M.F. Annealing carbon cluster ions: A mechanism for fullerene synthesis. J. Phys. Chem. 1994, 98, 1810–1818. [Google Scholar] [CrossRef]
  30. Lagow, R.J.; Kampa, J.J.; Wei, H.-C.; Battle, S.L.; Genge, J.W.; Laude, D.A.; Harper, C.J.; Bau, R.; Stevens, R.C.; Haw, J.F.; et al. Synthesis of linear acetylenic carbon: The “sp” carbon allotrope. Science 1995, 267, 362–367. [Google Scholar] [CrossRef]
  31. Homan, K.-H. Fullerenes and soot formation. New pathways to large particles in flame. Angew. Chem. Int. Ed. 1998, 37, 2434–2451. [Google Scholar] [CrossRef]
  32. Liang, C.; Allen, L.C. Double bond deformation: Cumulenes, cumulenones, and Group IV ethylene analogs. J. Am. Chem. Soc. 1991, 113, 1873–1878. [Google Scholar] [CrossRef]
  33. Raghavachari, K.; Binkley, J.S. Structure, stability, and fragmentation of small carbon clusters. J. Chem. Phys. 1987, 87, 2191–2197. [Google Scholar] [CrossRef]
  34. Roeges, N.P.G. A Guide to the Complete Interpretation of Infrared Spectra of Organic Structures; John Wiley & Sons: Chichester, UK, 1994. [Google Scholar]
  35. Horný, L.; Petraco, N.D.K.; Pak, C.; Schaefer, H.F., III. What is the nature of polyacetylene neutral and anionic chains HC2nH and HC2nH− (n = 6–12) that have recently been observed? J. Am. Chem. Soc. 2002, 124, 5861–5864. [Google Scholar]
  36. Szafert, S.; Gladysz, J.A. Carbon in one dimension: Structural analysis of the higher conjugated polyynes. Chem. Rev. 2003, 103, 4175–4205. [Google Scholar] [CrossRef]
  37. Osowska, K.; Lis, T.; Szafert, S. Protection/Deprotection-Free Syntheses and Structural Analysis of (Keto-aryl) diynes. Eur. J. Org. Chem. 2008, 27, 4598–4606. [Google Scholar] [CrossRef]
  38. Messerschmidt, M.; Scheins, S.; Luger, P. Charge density of (−)-strychnine from 100 to 15 K, a comparison of four data sets. Acta Cryst. 2005, B61, 115–121. [Google Scholar] [CrossRef]
  39. Munshi, P.; Guru Row, T.N. Topological analysis of charge density distribution in concomitant polymorphs of 3-acetylcoumarin, a case of packing polymorphism. Cryst. Growth Des. 2006, 6, 708–718. [Google Scholar] [CrossRef]
  40. Reji, T.; Lakshmi, S.; Pati, S.K.; Kulkarni, G.U. Role of Triple Bond in 1,2-Diphenylacetylene Crystal: A Combined Experimental andTheoretical Study. J. Phys. Chem. B 2006, 110, 24674–24677. [Google Scholar]
  41. Cremer, D.; Kraka, E. Role of triple bond in 1, 2-diphenylacetylene crystal: A combined experimental and theoretical study. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
  42. Bürgi, H.-B.; Capelli, S.C.; Goeta, A.E.; Howard, J.A.K.; Spackman, M.A.; Yufit, D.S. Electron Distribution and Molecular Motion in Crystalline Benzene: An Accurate Experimental Study Combining CCD X-ray Data on C6H6 with Multitemperature Neutron-Diffraction Results on C6D6. Chem. Eur. J. 2002, 8, 3512–3521. [Google Scholar] [CrossRef]
  43. Chopra, D.; Cameron, T.S.; Ferrara, J.D.; Guru Row, T.N. Pointers toward the Occurrence of C−F···F−C Interaction:  Experimental Charge Density Analysis of 1-(4-Fluorophenyl)-3,6,6-trimethyl-2-phenyl-1,5,6,7-tetrahydro-4H-indol-4-one and 1-(4-Fluorophenyl)-6-methoxy-2-phenyl-1,2,3,4-tetrahydroisoquinoline. J. Phys. Chem. A 2006, 110, 10465–10477. [Google Scholar] [CrossRef] [PubMed]
  44. Zhurova, E.A.; Matta, C.F.; Wu, N.; Zhurov, V.V.; Pinkerton, A.A. Experimental and theoretical electron density study of estrone. J. Am. Chem. Soc. 2006, 128, 8849–8861. [Google Scholar] [CrossRef] [PubMed]
  45. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  46. Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
  47. Becke, A.D. Density-functional thermochemistry III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  48. Lee, C.; Yang, W.; Parr, R.G. Density-functional exchange-energy approximation with correct asymptotic behaviour. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  49. Pauling, L. The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
  50. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  51. Mierzwicki, K.; Berski, S.; Latajka, Z. Nature of chemical bonds in MCCH (M = Li, Na, K) based on the topological analysis of electron localisation function (ELF) and electron density. Chem. Phys. Lett. 2000, 331, 538–546. [Google Scholar] [CrossRef]
  52. xd-a, version 4.10; Computer Program Package for Multipole Refinement and Anlysis of Electron Densities from Diffraction Data; Free University: Berlin, Germany, 1995.
  53. Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. 1978, A34, 909–921. [Google Scholar] [CrossRef]
  54. Bader, R.F. Atoms in Molecules—A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  55. CRYSTAL, version 2003; User’s Manual; University of Torino: Torino, Italy, 2003.
  56. Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
  57. Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theoret. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
  58. DGrid, version 4.2, Basin 4.2; Max Planck Institute for Chemical Physics of Solids: Dresden, Germany, 2007.
  59. The numerical grid value equaled 0.04 bohr was used. The “closed-shell” formula of ELF has been used.
  60. Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
  61. Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
  62. Gaussian, version 03, Revision D.02; Gaussian, Inc.: Wallingford, CT, USA, 2004.
  63. Molekel, version 4.1; Swiss National Supercomputing Centre: Manno, Switzerland, 2000–2001.
Sample Availability: Sample of the compound 1 is available from the authors.
Molecules 25 04388 g001 550
Figure 1. View of 1.
Figure 1. View of 1.
Molecules 25 04388 g001
Molecules 25 04388 g002 550
Figure 2. The final residue density (a) and the multipole deformation density (b) for 1.
Figure 2. The final residue density (a) and the multipole deformation density (b) for 1.
Molecules 25 04388 g002
Molecules 25 04388 g003 550
Figure 3. The electron density map ρbulk (r) of the R-(C11)-C(1)-C(2)-C(2A)-C(1A)-(C11A)-R fragment in the molecular plane. Lateral units in bohr and interval equal 0.005 e/bohr3.
Figure 3. The electron density map ρbulk (r) of the R-(C11)-C(1)-C(2)-C(2A)-C(1A)-(C11A)-R fragment in the molecular plane. Lateral units in bohr and interval equal 0.005 e/bohr3.
Molecules 25 04388 g003
Molecules 25 04388 g004 550
Figure 4. 3D plot of the Electron Localization Function (ELF) for 1 calculated at the B3LYP/6-311++G(d,p) computational level. The bonding localization domains V(C,C), V(C,H), non-bonding domains V1(O)∪V2(O) of the oxygen atoms, and core domains C(C), C(O) are visible. The basin populations for V(C,C) and V1(O)∪V2(O) are presented in the picture.
Figure 4. 3D plot of the Electron Localization Function (ELF) for 1 calculated at the B3LYP/6-311++G(d,p) computational level. The bonding localization domains V(C,C), V(C,H), non-bonding domains V1(O)∪V2(O) of the oxygen atoms, and core domains C(C), C(O) are visible. The basin populations for V(C,C) and V1(O)∪V2(O) are presented in the picture.
Molecules 25 04388 g004
Molecules 25 04388 g005 550
Figure 5. Percentage contributions of the Lewis structures representing the bonding in the R-(C11)-C(1)-C(2)-C(2A)-C(1A)-C(11A)-R carbon chain calculated using the basin populations ( N ¯ ) obtained from the topological analysis of the ELF function.
Figure 5. Percentage contributions of the Lewis structures representing the bonding in the R-(C11)-C(1)-C(2)-C(2A)-C(1A)-C(11A)-R carbon chain calculated using the basin populations ( N ¯ ) obtained from the topological analysis of the ELF function.
Molecules 25 04388 g005
Table
Table 1. Bond lengths in 1.
Table 1. Bond lengths in 1.
CRMP CRMP
O(1)-C(3)1.2231(8)1.2248(4)C(11)-C(12)1.4077(8)1.4080(5)
C(1)-C(2)1.2120(8)1.2169(4)C(11)-C(16)1.4055(8)1.4060(5)
C(1)-C(11)1.4300(9)1.4259(4)C(12)-C(13)1.3933(9)1.3934(4)
C(2)-C(2A)1.3670(11)1.3636(6)C(13)-C(14)1.3981(8)1.3987(4)
C(3)-C(4)1.5141(8)1.5109(4)C(14)-C(15)1.4039(8)1.4039(4)
C(3)-C(14)1.5016(9)1.5008(4)C(15)-C(16)1.3908(9)1.3924(4)
C(4)-C(5)1.5202(9)1.5237(5)
Table
Table 2. Pseudoatom charges for 1.
Table 2. Pseudoatom charges for 1.
AtomChargeAtomChargeAtomCharge
O(1)−0.59(5)C(12)0.10(4)H(51)0.12(9)
C(1)−0.30(4)C(13)0.04(4)H(52)−0.28(9)
C(2)−0.25(4)C(14)0.02(3)H(53)0.09(8)
C(3)0.05(4)C(15)0.14(5)H(12)0.06(6)
C(4)0.10(4)C(16)0.24(6)H(13)0.06(6)
C(5)0.30(6)H(41)0.07(6)H(15)0.06(6)
C(11)−0.05(3)H(42)0.16(5)H(16)−0.14(8)
Table
Table 3. Topological parameters of the charge distribution in 1.
Table 3. Topological parameters of the charge distribution in 1.
BondρcpΔρcpRijd1d2Hessian Eigenvaluesε
λ1λ2λ3
O(1)-C(3)2.78−6.31.22490.79440.4305−23.95−22.9340.590.04
C(1)-C(2)2.92−28.01.21700.64310.5739−18.45−18.148.540.02
C(1)-C(11)2.01−14.91.42600.72310.7029−13.43−12.8111.330.05
C(2)-C(2′)2.19−15.31.36360.68180.6818−13.95−13.3511.980.04
C(3)-C(4)1.77−12.61.51100.81740.6937−11.47−11.059.890.04
C(3)-C(14)1.85−14.81.50080.75210.7487−12.81−11.819.780.08
C(4)-C(5)1.66−10.21.52380.76550.7584−10.22−9.989.980.02
C(4)-H(41)1.97−19.71.08570.62400.4617−16.78−15.3312.370.09
C(4)-H(42)1.76−15.21.08400.68340.4006−15.43−14.5014.730.06
C(5)-H(51)2.08−22.71.08580.62760.4583−17.76−16.6411.730.07
C(5)-H(52)1.97−15.51.08510.54020.5449−15.04−13.9813.490.08
C(5)-H(53)1.94−19.11.08920.62960.4596−16.48−15.0512.450.10
C(11)-C(12)2.18−19.51.40810.72080.6873−15.57−13.619.680.14
C(11)-C(16)2.12−19.01.40610.68810.7180−15.36−13.139.520.17
C(12)-C(13)2.21−19.51.39360.68880.7048−15.48−13.809.780.12
C(12)-H(12)2.06−21.81.08350.61860.4649−17.36−16.8712.430.03
C(13)-C(14)2.14−18.81.39880.68110.7177−14.92−13.669.730.09
C(13)-H(13)2.08−22.71.08360.63830.4453−18.12−17.5913.040.03
C(14)-C(15)2.21−20.21.40410.69040.7137−15.73−14.069.610.12
C(15)-C(16)2.21−20.11.39240.67830.7141−15.81−13.669.380.16
C(15)-H(15)2.10−23.41.08340.60680.4766−17.76−17.4411.780.02
C(16)-H(16)2.20−23.41.08430.52320.5610−18.18−17.4112.210.04
Table
Table 4. Lattice energies (Ecryst) before and after counterpoise correction calculated with different exchange and correlational functionals (all energies are in kcal/mol) using the 6-31G(d,p) basis set. The experimental geometry has been adopted.
Table 4. Lattice energies (Ecryst) before and after counterpoise correction calculated with different exchange and correlational functionals (all energies are in kcal/mol) using the 6-31G(d,p) basis set. The experimental geometry has been adopted.
EnergySVWNPWGGAB3LYPB3PW
Ecryst−100.7−81.4−54.9−28.2
Ecryst + BSSE−78.3−58.1−32.3−8.4

Share and Cite

MDPI and ACS Style

Starynowicz, P.; Berski, S.; Gulia, N.; Osowska, K.; Lis, T.; Szafert, S. Is It Conjugated or Not? The Theoretical and Experimental Electron Density Map of Bonding in p-CH3CH2COC6H4-C≡C-C≡C-p-C6H4COCH3CH2. Molecules 2020, 25, 4388. https://doi.org/10.3390/molecules25194388

AMA Style

Starynowicz P, Berski S, Gulia N, Osowska K, Lis T, Szafert S. Is It Conjugated or Not? The Theoretical and Experimental Electron Density Map of Bonding in p-CH3CH2COC6H4-C≡C-C≡C-p-C6H4COCH3CH2. Molecules. 2020; 25(19):4388. https://doi.org/10.3390/molecules25194388

Chicago/Turabian Style

Starynowicz, Przemysław, Sławomir Berski, Nurbey Gulia, Karolina Osowska, Tadeusz Lis, and Sławomir Szafert. 2020. "Is It Conjugated or Not? The Theoretical and Experimental Electron Density Map of Bonding in p-CH3CH2COC6H4-C≡C-C≡C-p-C6H4COCH3CH2" Molecules 25, no. 19: 4388. https://doi.org/10.3390/molecules25194388

APA Style

Starynowicz, P., Berski, S., Gulia, N., Osowska, K., Lis, T., & Szafert, S. (2020). Is It Conjugated or Not? The Theoretical and Experimental Electron Density Map of Bonding in p-CH3CH2COC6H4-C≡C-C≡C-p-C6H4COCH3CH2. Molecules, 25(19), 4388. https://doi.org/10.3390/molecules25194388

Article Metrics

Back to TopTop