From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations
Abstract
:1. Introduction
2. Results and Discussion
2.1. Structure-H Hydrate of Neohexane
2.2. IR Spectra of Different sH Hydrate Structures at Equilibrium
Effect of Filling and Guest Type on the IR Spectra of sH Hydrate
2.3. Bond Strength and Hydrate’s Young’s Modulus from IR Spectra
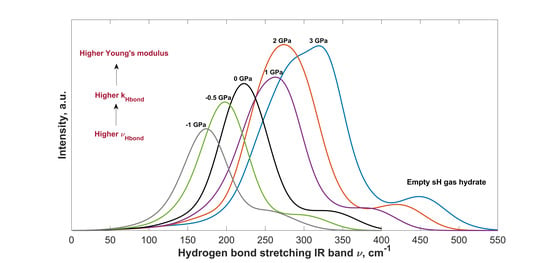
2.4. Effect of Hydrostatic Pressure on IR Spectra
2.4.1. Vibrational Frequencies and Intensities under Pressure
2.4.2. Change in Bond Strength and Young’s Modulus with Pressure
2.4.3. Vibrational Frequency vs. Interatomic Distances
2.4.4. sH Hydrate Vibrational Frequency Shifts
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sloan, E.D. Gas Hydrates: Review of Physical/Chemical Properties. Energy Fuels 1998, 12, 191–196. [Google Scholar] [CrossRef]
- Khokhar, A.; Gudmundsson, J.; Sloan, E. Gas Storage in Structure H Hydrates. Fluid Phase Equilibria 1998, 150, 383–392. [Google Scholar] [CrossRef]
- Lee, Y.; Seo, Y.-j.; Ahn, T.; Lee, J.; Lee, J.Y.; Kim, S.-J.; Seo, Y. CH4–Flue Gas Replacement Occurring in sH Hydrates and its Significance for CH4 Recovery and CO2 Sequestration. Chem. Eng. J. 2017, 308, 50–58. [Google Scholar] [CrossRef]
- Murayama, K.; Takeya, S.; Alavi, S.; Ohmura, R. Anisotropic Lattice Expansion of Structure H Clathrate Hydrates Induced by Help Guest: Experiments and Molecular Dynamics Simulations. J. Phys. Chem. C 2014, 118, 21323–21330. [Google Scholar] [CrossRef]
- Alavi, S.; Ripmeester, J.; Klug, D. Stability of Rare Gas Structure H Clathrate Hydrates. J. Chem. Phys. 2006, 125, 104501. [Google Scholar] [CrossRef]
- Ning, F.; Yu, Y.; Kjelstrup, S.; Vlugt, T.J.H.; Glavatskiy, K. Mechanical Properties of Clathrate Hydrates: Status and Perspectives. Energy Environ. Sci. 2012, 5, 6779. [Google Scholar] [CrossRef]
- Erfan-Niya, H.; Modarress, H. Molecular Dynamics Simulation of Structure H Clathrate-Hydrates of Binary Guest Molecules. J. Nat. Gas Chem. 2011, 20, 577–584. [Google Scholar] [CrossRef]
- Susilo, R.; Alavi, S.; Ripmeester, J.A.; Englezos, P. Molecular Dynamics Study of Structure H Clathrate Hydrates of Methane and Large Guest Molecules. J. Chem. Phys. 2008, 128, 194505. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Y.; Chen, G.; Hou, J.; Yan, Y.; Liu, H.; Li, S.; Zhang, J. Prediction of Efficient Promoter Molecules of sH Hydrogen Hydrate: An Ab Initio Study. Chem. Phys. 2019, 516, 15–21. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Y.; Zhang, J.; Xu, J.; Chen, G.; Hou, J. Theoretical Investigation of Storage Capacity of Hydrocarbon Gas in sH Hydrate. Chem. Phys. 2019, 525, 110393. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. Structural Properties of sH Hydrate: A DFT Study of Anisotropy and Equation of State. Mol. Simul. 2019, 45, 1524–1537. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. Elastic Properties and Anisotropic Behavior of Structure-H (sH) Gas Hydrate from First Principles. Chem. Eng. Sci. 2020, 227, 115948. [Google Scholar] [CrossRef]
- Hiratsuka, M.; Ohmura, R.; Sum, A.K.; Yasuoka, K. Vibrational Modes of Methane in the Structure H Clathrate Hydrate from Ab Initio Molecular Dynamics Simulation. J. Chem. Phys. 2012, 137, 144306. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.C. Infrared Spectral Interpretation: A Systematic Approach; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Chazallon, B.; Noble, J.A.; Desmedt, A. Spectroscopy of Gas Hydrates: From Fundamental Aspects to Chemical Engineering, Geophysical and Astrophysical Applications. In Gas Hydrates 1: Fundamentals, Characterization and Modeling, 1st ed.; Broseta, D., Ruffine, L., Desmedt, A., Eds.; ISTE Ltd.: London, UK; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 63–112. [Google Scholar]
- Rauh, F.; Mizaikoff, B. Spectroscopic Methods in Gas Hydrate Research. Anal. Bioanal. Chem. 2012, 402, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.M.; Wang, Y.; Liu, H.; Mancini, J.S. Ab Initio Quantum Approaches to the IR Spectroscopy of Water and Hydrates. J. Phys. Chem. Lett. 2015, 6, 366–373. [Google Scholar] [CrossRef]
- John, S.T. Vibrations of Methane in Structure I Clathrate Hydrate—An Ab Initio Density Functional Molecular Dynamics Study. J. Supramol. Chem. 2002, 2, 429–433. [Google Scholar]
- Martı’n-Llorente, B.; Fernández-Torre, D.; Ortega, I.K.; Escribano, R.; Maté, B. Vibrational Spectra of Crystalline Hydrates of Atmospheric Relevance: Bands of Hydrated Protons. Chem. Phys. Lett. 2006, 427, 300–304. [Google Scholar] [CrossRef]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. Infrared Spectra of Gas Hydrates from First-Principles. J. Phys. Chem. B 2019, 123, 936–947. [Google Scholar] [CrossRef]
- Kumar, R.; Lang, S.; Englezos, P.; Ripmeester, J. Application of the ATR-IR Spectroscopic Technique to the Characterization of Hydrates Formed by CO2, CO2/H2 and CO2/H2/C3H8. J. Phys. Chem. A 2009, 113, 6308–6313. [Google Scholar] [CrossRef]
- Rauh, F.; Pfeiffer, J.; Mizaikoff, B. Infrared Spectroscopy on the Role of Surfactants During Methane Hydrate Formation. RSC Adv. 2017, 7, 39109–39117. [Google Scholar] [CrossRef] [Green Version]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. THF Hydrates as Model Systems for Natural Gas Hydrates: Comparing Their Mechanical and Vibrational Properties. Ind. Eng. Chem. Res. 2019, 58, 16588–16596. [Google Scholar] [CrossRef]
- Cao, X.; Su, Y.; Liu, Y.; Zhao, J.; Liu, C. Storage Capacity and Vibration Frequencies of Guest Molecules in CH4 and CO2 Hydrates by First-Principles Calculations. J. Phys. Chem. A 2014, 118, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Uchida, T.; Ohmura, R.; Ikeda, I.Y.; Nagao, J.; Takeya, S.; Hori, A. Phase Equilibrium Measurements and Crystallographic Analyses on Structure-H Type Gas Hydrate Formed from the CH4−CO2−Neohexane−Water System. J. Phys. Chem. B 2006, 110, 4583–4588. [Google Scholar] [CrossRef]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. Effect of Guest Size on the Mechanical Properties and Molecular Structure of Gas Hydrates from First-Principles. Cryst. Growth Des. 2017, 17, 6407–6416. [Google Scholar] [CrossRef]
- Jendi, Z.M.; Servio, P.; Rey, A.D. Ideal Strength of Methane Hydrate and Ice Ih from First-Principles. Cryst. Growth Des. 2015, 15, 5301–5309. [Google Scholar] [CrossRef]
- Shimanouchi, T. Tables of Molecular Vibrational Frequencies; U.S. Dept. of Commerce, National Bureau of Standards: Washington, WA, USA, 1972. Available online: https://permanent.fdlp.gov/gpo23507/NSRDS-NBS-39.pdf (accessed on 8 February 2020).
- Benedict, W.S.; Gailar, N.; Plyler, E.K. Rotation-Vibration Spectra of Deuterated Water Vapor. J. Chem. Phys. 1956, 24, 1139–1165. [Google Scholar] [CrossRef]
- Zelsmann, H.R. Temperature Dependence of the Optical Constants for Liquid H2O and D2O in the Far IR Region. J. Mol. Struct. 1995, 350, 95–114. [Google Scholar] [CrossRef]
- Fukazawa, H.; Ikeda, S.; Mae, S. Incoherent Inelastic Neutron Scattering Measurements on Ice XI; the Proton-Ordered Phase of Ice Ih Doped with KOH. Chem. Phys. Lett. 1998, 282, 215–218. [Google Scholar] [CrossRef]
- Burnham, C.; Reiter, G.; Mayers, J.; Abdul-Redah, T.; Reichert, H.; Dosch, H. On the Origin of the Redshift of the OH Stretch in Ice Ih: Evidence from the Momentum Distribution of the Protons and the Infrared Spectral Density. Phys. Chem. Chem. Phys. 2006, 8, 3966–3977. [Google Scholar] [CrossRef]
- Gu, Q.; Trindle, C.; Knee, J.L. Communication: Frequency Shifts of an Intramolecular Hydrogen Bond as a Measure of Intermolecular Hydrogen Bond Strengths. J. Chem. Phys. 2012, 137, 091101. [Google Scholar] [CrossRef]
- Tulk, C.; Klug, D.; Ripmeester, J. Raman Spectroscopic Studies of THF Clathrate Hydrate. J. Phys. Chem. A 1998, 102, 8734–8739. [Google Scholar] [CrossRef]
- Hermansson, K.; Ojamäe, L. From Molecule to Cluster to Bulk: Water OH Vibrations in Different Surroundings. Int. J. Quantum Chem. 1992, 42, 1251–1270. [Google Scholar] [CrossRef]
- Choi, J.-H.; Cho, M. Computational IR Spectroscopy of Water: OH Stretch Frequencies, Transition Dipoles, and Intermolecular Vibrational Coupling Constants. J. Chem. Phys. 2013, 138, 174108. [Google Scholar] [CrossRef] [PubMed]
- Schicks, J.M.; Erzinger, J.; Ziemann, M.A. Raman Spectra of Gas Hydrates—Differences and Analogies to Ice 1h and (Gas Saturated) Water. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2005, 61, 2399–2403. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ojamaäe, L. Raman and IR Spectra of Ice Ih and Ice XI with an Assessment of DFT Methods. J. Phys. Chem. B 2016, 120, 11043–11051. [Google Scholar] [CrossRef] [Green Version]
- Synder, R.G.; Schachtschneider, J.H. A Valence Force Field for Saturated Hydrocarbons. Spectrochim. Acta 1965, 21, 169–195. [Google Scholar] [CrossRef]
- Mirkin, N.G.; Krimm, S. Ab Initio Analysis of the Vibrational Spectra of Conformers of Some Branched Alkanes. J. Mol. Struct. 2000, 550–551, 67–91. [Google Scholar] [CrossRef]
- Lin-Vien, D.; Colthup, N.B.; Fateley, W.G.; Grasselli, J.G. Chapter 2—Alkanes. In The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules; Lin-Vien, D., Colthup, N.B., Fateley, W.G., Grasselli, J.G., Eds.; Academic Press: San Diego, CA, USA, 1991; pp. 9–28. [Google Scholar]
- Greathouse, J.A.; Cygan, R.T.; Simmons, B.A. Vibrational Spectra of Methane Clathrate Hydrates from Molecular Dynamics Simulation. J. Phys. Chem. B 2006, 110, 6428–6431. [Google Scholar] [CrossRef]
- Kumar, R.; Englezos, P.; Moudrakovski, I.; Ripmeester, J.A. Structure and Composition of CO₂/H₂ and CO₂/H₂/C₃H₈ Hydrate in Relation to Simultaneous CO₂ Capture and H₂ Production. AIChE J. 2009, 55, 1584–1594. [Google Scholar] [CrossRef]
- Fleyfel, F.; Devlin, J.P. Carbon Dioxide Clathrate Hydrate Epitaxial Growth: Spectroscopic Evidence for Formation of the Simple Type-II Carbon Dioxide Hydrate. J. Phys. Chem. 1991, 95, 3811–3815. [Google Scholar] [CrossRef]
- Jones, D.R.H.; Ashby, M.F. Chapter 6—Physical Basis of Young’s Modulus. In Engineering Materials 1, 4th ed.; Jones, D.R.H., Ashby, M.F., Eds.; Butterworth-Heinemann: Oxford, UK, 2012; pp. 83–93. [Google Scholar]
- Vlasic, T.M.; Servio, P.; Rey, A.D. Atomistic Modeling of Structure II Gas Hydrate Mechanics: Compressibility and Equations of State. AIP Adv. 2016, 6, 085317. [Google Scholar] [CrossRef] [Green Version]
- Li, X.-Z.; Walker, B.; Michaelides, A. Quantum Nature of the Hydrogen Bond. Proc. Natl. Acad. Sci. USA 2011, 108, 6369–6373. [Google Scholar] [CrossRef] [Green Version]
- Hermansson, K.; Gajewski, G.; Mitev, P. Pressure-Induced OH Frequency Downshift in Brucite: Frequency-Distance and Frequency-Field Correlations. J. Phys. Conf. Ser. 2008, 117, 012018. [Google Scholar] [CrossRef]
- Umemura, J.; Birnbaum, G.; Bundle, D.; Murphy, W.; Bernstein, H.; Mantsch, H. The Correlation Between O—H Stretching Frequencies and Hydrogen Bond Distances in a Crystalline Sugar Monohydrate. Can. J. Chem. 1979, 57, 2640–2645. [Google Scholar] [CrossRef]
- Libowitzky, E. Correlation of OH Stretching Frequencies and OH···O Hydrogen Bond Lengths in Minerals. Mon. Für Chem. Chem. Mon. 1999, 130, 1047–1059. [Google Scholar] [CrossRef]
- Servio, P.; Lagers, F.; Peters, C.; Englezos, P. Gas Hydrate Phase Equilibrium in the System Methane-Carbon Dioxide-Neohexane and Water. Fluid Phase Equilibria 1999, 158, 795–800. [Google Scholar] [CrossRef]
- Ripmeester, J.A.; Ratcliffe, C.I. The Diverse Nature of Dodecahedral Cages in Clathrate Hydrates As Revealed by 129Xe and 13C NMR Spectroscopy: CO2 as a Small-Cage Guest. Energy Fuels 1998, 12, 197. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745–2779. [Google Scholar]
- Schaftenaar, G.; Noordik, J.H. Molden: A Pre-and Post-Processing Program for Molecular and Electronic Structures. J. Comput.-Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Okano, Y.; Yasuoka, K. Free-Energy Calculation of Structure-H Hydrates. J. Chem. Phys. 2006, 124, 024510. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Fernandez-Torre, D.; Escribano, R.; Archer, T.; Pruneda, J.; Artacho, E. First-Principles Infrared Spectrum of Nitric Acid and Nitric Acid Monohydrate Crystals. J. Phys. Chem. A 2004, 108, 10535–10541. [Google Scholar] [CrossRef]
- Benoit, D.M. Vibrational Signature of a Single Water Molecule Adsorbed on Pt (111): Toward a Reliable Anharmonic Description. J. Phys. Chem. A 2015, 119, 11583–11590. [Google Scholar] [CrossRef] [PubMed]
- Katari, M.; Nicol, E.; Steinmetz, V.; van der Rest, G.; Carmichael, D.; Frison, G. Improved Infrared Spectra Prediction by DFT from a New Experimental Database. Chem. A Eur. J. 2017, 23, 8414–8423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Sample Availability: Samples of the compounds are not available from the authors. |











| sH Hydrate | a, Å | c, Å | V, Å3 | O···O, Å | O···H, Å | O-H, Å |
|---|---|---|---|---|---|---|
| Empty | 11.93 | 9.76 | 1206.15 | 2.702 | 1.698 | 1.009 |
| CH4-NH | 12.33 | 10.12 | 1330.95 | 2.792 | 1.797 | 1.000 |
| Xe-NH | 12.48 | 10.10 | 1349.53 | 2.806 | 1.810 | 1.000 |
| CO2-NH | 12.86 | 9.88 | 1350.21 | 2.808 | 1.813 | 0.999 |
| CO2-CH4-NH | 12.37 | 10.05 | 1334.05 | 2.795 | 1.799 | 1.000 |
| sH Hydrate | Hbond Stretch | H2O Libration | H2O Bending | OH Sym. Stretch | OH Asym. Stretch | |
|---|---|---|---|---|---|---|
| Empty | 223 | 703 | 1009 | 1640 | 2954 | 3204 |
| CH4-NH | 186 | 657 | 904 | 1636 | 3067 | 3269 |
| Xe-NH | 186 | 645 | 892 | 1626 | 3119 | 3314 |
| CO2-NH | 182 | 615 | 886 | 1629 | 3102 | 3283 |
| CO2-CH4-NH | 183 | 622 | 898 | 1635 | 3067 | 3272 |
| sH Hydrate | C-C-C Bend | CO2 Bend | CH2/CH3 Rock | CH4 Bend | CH3 Sym. Bend | CH3 Asym. Bend | CH4 Rock | CO2 Asym. Stretch |
|---|---|---|---|---|---|---|---|---|
| CH4-NH | 408/474 | - | 1196 | 1252 | 1344 | 1431 | 1478 | - |
| Xe-NH | 406/483 | - | 1209 | - | 1347 | 1435 | - | - |
| CO2-NH | 404/480 | * | 1203 | - | 1344 | 1430 | - | 2284 |
| CO2-CH4-NH | 408/474 | * | 1196 | 1251 | 1344 | 1430 | 1478 | 2284 |
| sH Hydrate | k, N.m−1 | E (IR Analysis), GPa | E (Elastic Constants), GPa [12] |
|---|---|---|---|
| Empty | 2.778 | 16.36 | 14.317 |
| CH4-NH | 1.933 | 10.76 | 16.569 |
| Xe-NH | 1.933 | 10.68 | 17.002 |
| CO2-NH | 1.850 | 10.20 | - |
| CO2-CH4-NH | 1.871 | 10.40 | - |
| Guest Vibrational Frequencies, cm−1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Pressure, GPa | C-C-C Bend | CO2 Bend | CH2/CH3 Rock | CH4 Bend | CH3 Sym. Bend | CH3 Asym. Bend | CH4 Rock | CO2 Asym. Stretch |
| Xe-NH sH Hydrate | ||||||||
| −1 | 404/479 | - | 1204 | - | 1349 | 1437 | - | - |
| −0.5 | 405/480 | - | 1207 | - | 1348 | 1434 | - | - |
| 0 | 406/483 | - | 1209 | - | 1347 | 1435 | - | - |
| 1 | 408/488 | - | 1214 | - | 1350 | 1439 | - | - |
| 2 | 491 | - | - | - | 1353 | 1442 | - | - |
| 2.9 | 494 | - | - | - | 1353 | 1443 | - | - |
| 4 | - | - | - | - | 1354 | 1447 | - | - |
| CO2-NH sH Hydrate | ||||||||
| −0.955 | 403/475 | - | 1197 | - | 1343 | 1428 | - | 2270 |
| −0.5 | 403/477 | - | 1201 | - | 1344 | 1429 | - | 2278 |
| 0 | 404/480 | - | 1203 | - | 1344 | 1430 | - | 2284 |
| 1 | 404/482 | 612 | 1206 | - | 1346 | 1432 | - | 2292 |
| 2 | 483 | 609 | - | - | 1346 | 1433 | - | 2299 |
| 3 | 486 | 607 | - | - | 1347 | 1435 | - | 2304 |
| CO2-CH4-NH sH Hydrate | ||||||||
| −0.5 | 405/472 | - | 1194 | 1250 | 1343 | 1429 | 1477 | 2277 |
| 0 | 408/474 | - | 1196 | 1251 | 1344 | 1430 | 1478 | 2284 |
| 2 | 478 | 611 | 1199 | 1255 | 1345 | 1433 | 1483 | 2301 |
| 3 | 479 | 610 | - | 1253 | 1346 | 1434 | 1484 | 2308 |
| Empty sH | Pressure, GPa | k, N.m−1 | E, GPa |
| −1.405 | 0.778 | 3.92 | |
| −1 | 1.691 | 9.30 | |
| −0.5 | 2.190 | 12.53 | |
| 0 | 2.778 | 16.36 | |
| 1 | 3.864 | 23.65 | |
| 2 | 4.194 | 26.48 | |
| 3 | 5.685 | 36.81 | |
| Xe-NH sH | −1 | 1.003 | 5.16 |
| −0.5 | 1.308 | 7.02 | |
| 0 | 1.933 | 10.68 | |
| 1 | 2.394 | 13.79 | |
| 2 | 3.164 | 18.81 | |
| 2.9 | 4.012 | 24.38 | |
| 4 | 4.164 | 25.90 | |
| CO2-NH sH | −0.955 | 0.652 | 3.27 |
| −0.5 | 1.342 | 7.15 | |
| 0 | 1.850 | 10.20 | |
| 1 | 2.704 | 15.59 | |
| 2 | 3.381 | 20.09 | |
| 3 | 3.747 | 22.81 | |
| CO2-CH4-NH sH | −0.5 | 1.325 | 7.11 |
| 0 | 1.871 | 10.40 | |
| 2 | 3.548 | 21.26 | |
| 3 | 3.983 | 24.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daghash, S.M.; Servio, P.; Rey, A.D. From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations. Molecules 2020, 25, 5568. https://doi.org/10.3390/molecules25235568
Daghash SM, Servio P, Rey AD. From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations. Molecules. 2020; 25(23):5568. https://doi.org/10.3390/molecules25235568
Chicago/Turabian StyleDaghash, Shaden M., Phillip Servio, and Alejandro D. Rey. 2020. "From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations" Molecules 25, no. 23: 5568. https://doi.org/10.3390/molecules25235568
APA StyleDaghash, S. M., Servio, P., & Rey, A. D. (2020). From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations. Molecules, 25(23), 5568. https://doi.org/10.3390/molecules25235568