Next Article in Journal
Antimicrobial, Antioxidant, and Anticancer Activities of Some Novel Isoxazole Ring Containing Chalcone and Dihydropyrazole Derivatives
Next Article in Special Issue
A Halogen Bonding Perspective on Iodothyronine Deiodinase Activity
Previous Article in Journal
Chemometrics-Assisted Identification of Anti-Inflammatory Compounds from the Green Alga Klebsormidium flaccidum var. zivo
Previous Article in Special Issue
Anion Recognition by Neutral and Cationic Iodotriazole Halogen Bonding Scaffolds
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 25
Issue 5
10.3390/molecules25051045
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Application of Halogen Bonding to Organocatalysis: A Theoretical Perspective

by
Hui Yang
and
Ming Wah Wong
*
Department of Chemistry, National University of Singapore, 3 Science Drive 3, Singapore 117543, Singapore
*
Author to whom correspondence should be addressed.
Molecules 2020, 25(5), 1045; https://doi.org/10.3390/molecules25051045
Submission received: 30 December 2019 / Revised: 23 February 2020 / Accepted: 24 February 2020 / Published: 26 February 2020
(This article belongs to the Special Issue Halogen Bonding: Insights from Computational Tools)
Browse Figures
Versions Notes

Abstract

:
The strong, specific, and directional halogen bond (XB) is an ideal supramolecular synthon in crystal engineering, as well as rational catalyst and drug design. These attributes attracted strong growing interest in halogen bonding in the past decade and led to a wide range of applications in materials, biological, and catalysis applications. Recently, various research groups exploited the XB mode of activation in designing halogen-based Lewis acids in effecting organic transformation, and there is continual growth in this promising area. In addition to the rapid advancements in methodology development, computational investigations are well suited for mechanistic understanding, rational XB catalyst design, and the study of intermediates that are unstable when observed experimentally. In this review, we highlight recent computational studies of XB organocatalytic reactions, which provide valuable insights into the XB mode of activation, competing reaction pathways, effects of solvent and counterions, and design of novel XB catalysts.

Graphical Abstract

1. Introduction

Halogen bonding attracted growing interest in recent years, due to its wide range of applications as highly directional motifs in supramolecular chemistry, crystal engineering, materials science, organocatalysis, and drug design [1]. Halogen bond (XB) is defined by the International Union of Pure and Applied Chemistry (IUPAC) as “a net attractive interaction between an electrophilic region associated with a halogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity” [2]. Essentially, the halogen atom serves as an electron-deficient moiety (XB-donor) to interact with a nucleophilic region of a Lewis base (XB-acceptor) to form a halogen bond (Figure 1). Since XB interaction features high directionality, it has excellent molecular recognition ability.
The σ-hole concept of Politzer et al. [3,4] represents the most widely accepted model to explain the origin of the halogen bond. In this model, the halogen atom is characterized by anisotropic distribution of electron density with a localized region of positive electrostatic potential (ESP) along the extension of the R–X bond (Figure 1). This model readily accounts for the close contact between halogen and nucleophile (Nu), as well as the linearity of the R–X…Nu angle. The magnitude of the σ-hole of XB-donors, which affects the strength of XB, depends on two key electronic factors: (i) polarizability of the halogen atom (X = I > Br > Cl > F), and (ii) electron-withdrawing ability of the group bonded to the halogen. The origin of halogen bond can also be explained by molecular orbital theory [5,6,7]. The σ* orbital of a halogen atom (i.e., the lowest unoccupied molecular orbital (LUMO) of R–X) interacts with an electron pair (lone pair or π bond) of a nucleophile (i.e., the highest occupied molecular orbital (HOMO) of Nu) leading to stabilizing the HOMO–LUMO interaction (Figure 1). The stronger frontier orbital interaction derives from the lower energy of the σ* LUMO of R–X. Thus, this model also explains the trend of XB strength for XB-donors I > Br > Cl > F and linearity of XB interaction. It is important to note that the molecular orbital interaction provides a proper description of the charge transfer contribution in XB formation. Various energy decomposition analyses showed strong supporting evidence for the role of charge transfer [8,9,10]. In particular, the frontier orbital interaction explains the site specificity of XB involving aromatic XB-acceptors, while the electrostatic model based on ESP fails to explain the site specificity [5]. Intriguingly, a few examples of strong halogen bonds with a large degree of covalency were reported [11,12,13], e.g., the N∙∙∙Br bond in bis(3-methylpyridine)bromonium perchlorate [13]. The XB interaction of this type is better represented as a coordinate (dative covalent) bond (XBA→XBD), rather than the significantly less covalent interaction (XBA∙∙∙XBD). We note that all these strong XB-bonded systems are charge-assisted XB interactions. The molecular orbital model (Figure 1) readily explains the strong donor–acceptor interaction with a large degree of charge transfer.
The parallel between the hydrogen bond (HB) and halogen bond in terms of high directionality and strength is well recognized [7,14,15]. Although the XB is generally weaker than the corresponding HB, XB has a stronger directionality. In addition, XB has a unique feature of tenability of the halogen donor as compared to hydrogen in HB. As a consequence, the halogen bonding interaction is considered to be a promising alternative to the hydrogen bonding interaction in catalysis. The haloperfluoroalkane-catalyzed reduction of quinoline derivatives using Hantzsch ester by Bolm et al. in 2008 represents the seminal work in applying XB to organocatalysis [16]. Subsequently, several groups made substantial contributions to halogen bonding in organocatalysis. These authors developed a variety of XB-donors bearing strong electron-withdrawing moieties such as perfluoro-aryls or cationic heterocycles to form strong XB with Lewis basic substrates. This led to the development of new methods in organic synthesis, e.g., nucleophilic substitution/addition, cyclization, and transfer hydrogenation reactions. Several recent excellent reviews were published on the experimental studies on XB organocatalysis [17,18]. As this review focuses on the computational studies on XB organocatalysis, we do not discuss the experimental studies in detail and ask the readers to read these reviews to appreciate the progress in recent years.
In the early proof-of-principle stage of halogen bond catalysis, starting from the pioneering work of Bolm et al. (Scheme 1) [16], mechanistic studies were almost exclusively conducted in experiments. The catalysts’ ability to form halogen bonds was unambiguously established via X-ray crystallography studies [19,20,21,22,23,24,25,26,27,28,29], which clearly showed the close contacts between halogen atoms and counter anions in the case of ionic catalysts, or other XB-acceptors in the case of neutral ones. In addition, NMR studies allowed probing the interaction between XB catalysts and substrates in various organic solvents [30,31]. Together with isothermal calorimetric titration [21,32], these experiments allowed the binding constants of XB-donors and XB-acceptors to be experimentally determined. Some of the largest binding constants determined experimentally are on the order of 103 M−1 at room temperature, e.g., XB binding between tridentate polyfluorinated XB-donors and nitrogen-based XB-acceptors in non-polar organic solvents [22]. Taken together, these experimental studies provided strong support to the hypothesized halogen bond binding, which is the basis of XB catalysis. Furthermore, carefully designed control experiments were conducted, whose results showed that the halogen bond catalysis pathway was probably the most favorable one among a few other viable competitive pathways, e.g., Brønsted acid pathway and radical pathway [19,33,34].
Computational chemistry provides a useful and complementary role in understanding the mechanistic features of XB catalysis. Firstly, reliable quantum chemical calculations aid in understanding the thermodynamics and kinetics of catalytic reactions. Secondly, theory enables the characterization of the transition state, which is crucial in the understanding of the XB mode of activation and stereoselectivity. Thirdly, electronic structure calculations help to understand the governing factors in stabilizing the transition state, which in turn shed light on the origin of reactivity and stereoselectivity. Finally, theoretical calculations can be employed to design novel XB catalysts. Numerous computational studies on XB-based organocatalytic reactions demonstrated that quantum chemical calculations provide important insight into the XB mode of activation, competing reaction pathways, effects of solvent and counterions, and design of novel XB catalysts. Herein, we present a brief review of recent computational studies on this subject. Special emphasis is placed on theoretical calculations which elucidate the role of XB activation, allowing for a careful comparison with uncatalyzed reactions and competing reaction pathways.

2. Computational Methods for XB Organocatalysis

Over the past decade, a large number of computational studies were reported for halogen-bonded systems and various XB applications. One of the most accurate quantum chemical methods is CCSD(T), coupled cluster with single, double, and perturbative triple excitations [35]. Unfortunately, it is expensive and not practical for normal application studies. Thus, it is mainly used for benchmarking purposes for small halogen-bonded systems [36,37,38,39]. Density functional theory (DFT) methods are popular alternatives because they provide sufficient accuracy with significantly lower computational expense. Based on an extensive comparison of wave function and DFT methods on geometries and dissociation energies of halogen-bonded systems, Kozuch and Martin concluded that functionals with high exact exchange or long-range corrections, e.g., M06-2X [40], ωB97XD [41], and double hybrids, are suitable [36]. As the M06-2X functional and other latest versions of Minnesota functionals, e.g., MN15 [42], are well parametrized for noncovalent interactions and kinetics [36,37,38], M06-2X is a popular choice for studying XB organocatalysis [43]. For liquid-phase studies, the SMD universal solvation model [44] is a popular method to study the implicit solvation effect. Engelage et al. showed that the standard radii for bromine and iodine are incorrect, and the authors redefined the SMD parameters for these two halogen atoms [45]. While the majority of the reviewed papers in this article employed DFT methods, we note that the recently developed domain-based local pair–natural coupled cluster (DLPNO-CCSD(T)) method [46] is a very promising method in terms of speed and accuracy [47]. The DLPNO-CCSD(T) energy reproduces more than 99.9% of the CCSD(T) correlation energy at a computational cost of only 2–4 times that of a typical DFT method [48]. Bickelhaupt and co-workers applied this state-of-the-art method in a recent computational study on halogen bond organocatalysis [49].
To gauge the performance of various computational methods, we computed here the XB binding free energies (ΔG298) between iodopentafluorobenzene and triethylamine using a few popular DFT and Grimme’s dispersion-corrected [50] functionals, namely, B3LYP, B3LYP-D3, M06-2X, MN15, ω-B97XD, PBE0, and PBE0-D3, together with a moderately large 6-311++G(2d,p) basis set (Table 1). These values were benchmarked against an experimentally determined binding free energy at 298 K in cyclohexane [51]. As evidenced in Table 1, most DFT-calculated binding free energies (ΔG298 in cyclohexane) are in agreement with the experimental value except for the methods without dispersion correction. Recent theoretical studies [38] highlighted the importance of dispersion for accurate description of halogen bonding interactions. It is important to note that the entropic corrections to binding free energy are fairly large (9–10 kcal/mol) for all DFT methods (Table 1). Thus, it is essential to include the entropic contribution for comparison with experiment.

3. Computational XB Organocatalysis Studies

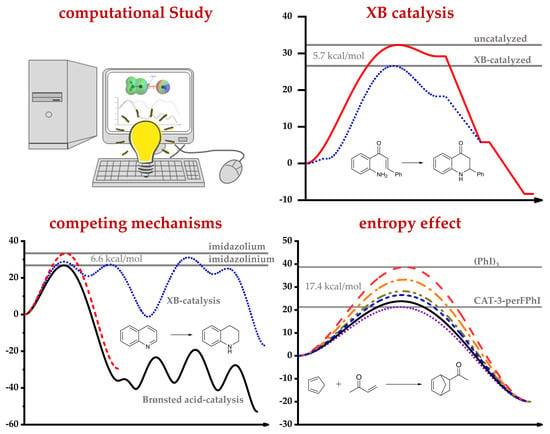
3.1. Transition State and Binding XB Complex Studies

Along with the experimental development of halogen bond catalysis, computational studies are playing an increasingly important role in establishing XB catalysis. For many catalyzed reactions reported by Huber et al., calculations of catalyzed transition states (TSs) or binding complexes were often performed to further support the hypothesized XB catalysis pathway (Figure 2) [23,52,53,54,55,56]. For the investigated halogen bond catalysts, especially those of bidentate and tridentate nature, calculated structures helped chemists to gain important insights, e.g., the number of halogen bonds formed and XB-acceptor atoms involved, XB interaction distances, and structural changes upon binding. These important structural insights are difficult to obtain through experimental means. While computational studies calculating XB-catalyzed TSs and/or binding complexes will continue to be an important tool to help understand XB activation, we believe that there is high demand for fuller and more comprehensive computational studies of reaction mechanisms, particularly those that calculate and compare different possible pathways. Insights from such studies could help understand the anion effect, catalyst substituent effect, solvent effect, and reaction kinetics. When combined with experiments, they can potentially lead to discovery of better catalysts. Currently, there are only a small number of such computational studies. Not surprisingly, the iodine atom, being the strongest XB-donor among the halogens, is the focus of almost all the studies.
At the start of halogen bond catalysis, the catalysts employed were neutral XB-donors [16,20,57]. At length, it was discovered experimentally that charge-enhanced XB catalysts are more potent donors than the charge-neutral ones, as the latter often failed to give any detectable product yields in a few reported experimental attempts [19,21,23,25,58]. Despite the comparatively weaker donor strength, neutral XB catalysts have several advantages over cationic catalysts. They dissolve better in organic solvents, and they are more stable and less prone to decomposition or other side reactions. Most importantly, there is less mechanistic consideration regarding the mode of activation of a neutral XB catalyst than a cationic type.
Among the neutral XB catalysts, molecular iodine, which is perhaps the simplest iodine-based donor, was an active reagent in a wide range of organic reactions [59,60,61,62,63,64]. The earliest example of catalysis by molecular iodine in the dehydration of diacetone alcohol was discovered back in 1915 [65]. Other catalytic reactions followed. However, the mechanisms of these catalytic reactions were often not well understood, and different mechanisms were often proposed for the same reactions, all with partial experimental support. While the majority of halogen bonds reported so far are based on iodine (I), there are a few studies of hypervalent iodine(III)-catalyzed reactions [57,66]. The activation of substrates was also proposed to originate from the halogen bond.
In this review, we cover and discuss iodine-based catalysts in three sections, emphasizing the mechanistic aspects, especially in terms of a comparison to uncatalyzed and other plausible side reactions. The first section deals with computational mechanistic studies of neutral halogen bond catalysts, including molecular iodine, the second section deals with ionic XB catalysts, and the third section deals with hypervalent iodine(III) catalysts.

3.2. Neutral Halogen Bond Catalysts

3.2.1. Computational Study of XB-Catalyzed Hydrocyanation of Imines

Hydrocyanation of imines is an important reaction to synthesize amino acids [67]. Recently, Heinz et al. reported a computational investigation of feasibility of the reaction being catalyzed by neutral fluoroiodobenzene catalysts 9–12 (Scheme 2) [68].
The DFT method BP86 [69], together with the def2-TZVP basis set for all atoms and ecp-28-mdf pseudopotential for iodine, was used. Both gas- and solution-phase energies were computed. In the latter case, the conductor-like screening model (COSMO) polarizable continuum model (PCM) was employed to study the solvent effect of the calculated gas-phase structures, with toluene used as a solvent. Zero-point energy correction was included in the calculated energies.
The authors firstly investigated the uncatalyzed hydrocyanation reaction in both the gas phase and in toluene (Figure 3). Catalyzed reactions by four XB catalysts (9–12) were next investigated, and results indicated that all catalysts lowered the activation energy in toluene significantly, with 12, having the most electron-withdrawing aryl ring, lowering it the most by 10.6 kcal/mol and 9 the least by 4.8 kcal/mol.
The reduction of reaction barrier of hydrocyanation reaction of imine by 4–10 kcal/mol via XB catalysis using various fluoroiodobenzenes (9–12) seems to be a remarkable result, given their monodentate nature. Experimentally, only in a very few cases were monodentate XB compounds found to be catalytic [16,26,70]. However, these calculations were performed without considering the effect of entropy (see Table 1), which cannot be ignored when comparing catalyzed to uncatalyzed reactions. Furthermore, the reference points of the reaction profiles were chosen to be the weakly hydrogen bonded (6-I1) or halogen-bonded complexes (6-I1-XB) rather than the usual free reactants and catalysts. Hence, the conclusion is likely to change upon inclusion of entropy correction and optimization in a solvent medium.

3.2.2. Computational Design of Neutral XB Catalysts

In 2016, our group reported a computational study of an in silico designed tridentate halogen bond catalyst, with due consideration of reaction free energies and reaction kinetics [71]. All the calculations were performed using the M06-2X functional. For geometry optimizations, a small basis set, 6-31G(d) for non-iodine atoms and aug-cc-pVTZ for iodine, referred to as the SMALL basis set, was used, while, for single-point energy calculations, a large one, 6-311+G(d,p) for non-iodine atoms and aug-cc-pVTZ for iodine, referred to as the BIG basis set, was used. Reported relative free energies correspond to the M06-2X/BIG//M06-2X/SMALL level of theory at 298.15 K.
Firstly, Diels–Alder addition between cyclopentadiene (13) and buten-2-one (14) was studied. The effect of increasing the number of XBs on the reaction activation free energy was examined, by adding one more iodobenzene molecule systematically as the catalytic system (up to three iodobenzene molecules). It was observed that the activation enthalpy is decreased by about 4–5 kcal/mol for each addition of iodobenzene, in line with the increased number of XBs. However, bringing together catalyst and substrates in the tightly bound TS leads to a notable decrease in entropy, the effect of which cannot be ignored. Indeed, the activation free energy increases by 5 kcal/mol for each addition of iodobenzene (Figure 4).
One plausible strategy to overcome the unfavorable entropy effect is to design a molecule with a suitable geometric arrangement that could form three XBs at the same time. The unfavorable entropy contribution would be paid for in the synthesis stage when the three donors are brought together. Accordingly, a tripodal catalyst CAT-3-perFPhI (18) was designed, incorporating three fluorinated iodobenzene moieties (Figure 4). When the test Diels–Alder reaction was calculated for CAT-3-perFPhI, a lowered reaction free energy barrier of 21.3 kcal/mol was obtained, compared to 23.8 kcal/mol for the uncatalyzed reaction, indicating the success of the design introducing multiple XBs simultaneously to reduce the entropy penalty. Importantly, the interaction distances of three XBs observed in CAT-3-perFPhI-TS-endo, measured at 2.98, 3.00, and 3.61 Å, are very close to the corresponding distances in PhI-3-TS-endo, at 2.96, 3.01, and 3.73 Å (Figure 5). The XB strengths in CAT-3-perFPhI-TS-endo were estimated using a fragment-based approach to be 6.6, 6.2, and 4.1 kcal/mol, respectively.
The reaction kinetics was also assessed for the uncatalyzed and CAT-3-perFPhI-catalyzed Diels–Alder reaction, using the energetic span model of Shaik and Kozuch [72,73,74]. It was found that the computed turnover frequency (TOF) for the catalyzed reaction increases with decreasing temperature, while, for the uncatalyzed reaction, the rate constant decreases with decreasing temperature. For instance, upon lowering the temperature from 298.15 to 248.15 K, TOF for the catalyzed reaction increases from 5.5 h−1 to 28 h−1; for the uncatalyzed reaction, the rate constant decreases from 5.7 × 10−2 to 1.9 × 10−3 M·h−1.
Results from SMD modeling of common organic solvents chloroform and n-hexane showed that free energy of activation for both uncatalyzed and CAT-3-perFPhI-catalyzed reactions increases compared to the gas-phase results, and the catalyzed reaction is still faster in both solvents.
Catalysis by CAT-3-perFPhI of a Claisen rearrangement reaction was also studied (Table 2). In n-hexane, the catalyzed reaction was predicted to have a slightly higher reaction barrier of 28.3 kcal/mol at 318 K than 26.5 kcal/mol for the uncatalyzed reaction, but TOF of the catalyzed reaction is in the same order of magnitude as the kKeq of the uncatalyzed reaction. TOF calculations showed that, when the temperature is lowered to 273 K, TOF of the catalyzed reaction becomes two orders of magnitude higher than kKeq of the uncatalyzed reaction, allowing for catalytic Claisen rearrangement by CAT-3-perFPhI.
It should be noted that, when compared to the similar and well-studied H-bond catalysis [75,76,77,78,79,80], there are far fewer studies of catalysts design based on XB. The larger sizes of halogen atoms and the more stringent structural requirement of XB make the design of multidentate XB catalysts more challenging. Despite being able to form three XBs simultaneously, the designed neutral tridentate catalyst CAT-3-perFPhI (18) only lowers the reaction barrier of the benchmark Diels–Alder reaction by 2.5 kcal/mol (Figure 4). This is to be compared to the bidentate cationic catalyst developed by Huber’s group, which lowers the reaction barrier of the same reaction by 3.0 kcal/mol (Figure 2a) [52], in agreement with experimental observation that cationic XB catalysts are more potent than neutral ones. However, as noted in Section 3.1, there are several advantages of neutral XB catalysts, which still make them an attractive target for catalyst design. As of today, the designed catalyst is yet to be synthesized and verified experimentally.

3.2.3. I2 as an XB Catalyst in Organic Reactions

In recent years, much effort was devoted to computational and experimental studies of the mechanism of I2-catalyzed reactions. By far, the most comprehensive computational mechanistic study was carried out by the Breugst group [81], who investigated the mechanism of four different organic transformations apparently catalyzed by molecular iodine at the B2PLYP-D3/aug-cc-pVTZ/IEFPCM//M06-2X-D3/6-311+G(d,p)/IEFPCM level, with the aug-cc-pVTZ-pp basis set for iodine atoms.
The first reaction studied was intramolecular cyclization of aminochalcone (Figure 6). The mechanism of the uncatalyzed reaction was explored initially, and the free energy barrier of the intramolecular nucleophilic addition of the aniline moiety on the Michael acceptor was determined to be rather high at 32.3 kcal/mol, explaining why the reaction does not occur without a catalyst. Subsequent proton transfer and tautomerization furnish the product.
In the I2-catalyzed cyclization, the free energy barrier of the nucleophilic addition step is lowered by 5.7 kcal/mol compared to the uncatalyzed reaction of 26.6 kcal/mol. The authors attributed this to the stabilization of the developing partial negative charge on the Michael acceptor by a very short halogen bond to I2, measured at 2.47 Å.
Similarly, I2 was found to lower the free energy barrier of intermolecular Michael addition of pyrrolidine to methyl acrylate, from 18.3 kcal/mol of the uncatalyzed reaction to 15.9 kcal/mol, of intermolecular Michael addition of methyl pyrrole to nitrostyrene from 26.6 kcal/mol to 24.7 kcal/mol, and of intermolecular Michael addition of indole to trans-crotonophenone from 34.7 kcal/mol to 27.1 kcal/mol (Figure 7).
Analysis of the halogen bonding interaction of various species of two selected reactions by natural bond orbital (NBO) population analysis [82] showed that XB interaction energies increase along the reaction profile, in line with the developing partial negative charges on corresponding XB-donors. The interaction energies could reach a remarkable magnitude of more than 50 kcal/mol in the zwitterionic intermediates (Figure 8).
One other possible mechanistic pathway, namely, hidden Brønsted acid catalysis, was also investigated. Several possible pathways to generate hydroiodic acid (HI) were calculated but were found to be highly endergonic. Nevertheless, the authors calculated HI-catalyzed addition of indole to trans-crotonophenone (Figure 7) and found that HI is also an excellent catalyst for this reaction. The reaction barrier is even slightly lower than the I2-catalyzed pathway, with 22.6 kcal/mol for the former versus 27.1 kcal/mol for the latter. To help determining the reaction mechanism, the authors carried out careful experiments to directly compare the reaction rates of I2 and HI-catalyzed reactions in acetonitrile. Results showed that I2 gave on average 72% ± 3% yield in 3 min while HI gave only 40% ± 3% yield for the same duration, in support of the XB catalysis mechanism. In 2017, the same group performed a detailed experimental investigation and, based on their new experimental result, they ruled out the Brønsted acid catalysis in favor of the XB catalysis mechanism [33].

3.2.4. I2-Catalyzed iso-Nazarov Cyclization of Conjugated Dienals

The XB-catalyzed Nazarov cyclization attracted much attention recently [54,83,84]. Breugst and co-workers reported a combined experimental and computational study of I2-catalyzed Nazarov cyclization [84]. Based on their results of kinetic studies, i.e., the reaction being first order in I2, and the reaction barrier, as well as comparative control studies, the authors could rule out the Brønsted acid pathway in favor of the XB pathway. Their calculated activation barrier of the XB pathway (84 kJ/mol) is in close agreement with the experimental determined value (ΔG≠298 = 86.8 kJ/mol). The reaction profile and transition state structure are similar to those presented in Figure 6.
Riveira and coworkers recently studied a similar I2-catalyzed iso-Nazarov cyclization of conjugated dienals at the PCM (ethyl acetate)/M06-2X/6-311+G(d,p) (aug-cc-pVTZ-PP basis set for I) level (Figure 9) [83]. The reaction barrier (ΔG≠393) of I2-catalyzed cyclization of 31a was computed to be quite high at 29.9 kcal/mol, although it is lower than the barrier of the uncatalyzed reaction at 38.1 kcal/mol. The authors then proposed a new catalytic pathway involving two I2 molecules in the cyclization step TS, namely, 31b-TS (Figure 9). The reaction barrier was further reduced by 5.8 kcal/mol to 24.1 kcal/mol. In further support of this proposed pathway, the reaction barrier for the substrate of 31c (R = H) was computed to be very high at 32.6 kcal/mol, in line with the experimental finding where only traces amount of product could be obtained for this substrate.
It should be noted that the reference used to calculate reaction barriers is the XB-bonded pre-TS complexes rather than the free catalyst and substrates. The complexation process of catalysts and substrates via halogen bond is not necessarily favorable in terms of free energy [81]. Use of binding complexes as an energy reference might lead to an inaccurate comparison between pathways that differ in molecularity, resulting in a bias favoring higher-molecularity pathways. As pointed out in our early discussion, Breugst et al. determined the reaction order with respect to molecular iodine for a similar Nazarov cyclization reaction to be one.

3.2.5. Dihalogen-Catalyzed Michael Addition Reactions

By far, the majority of computational and experimental studies of XB catalysis focused on the element iodine. In 2019, Bickelhaupt and co-workers reported a comprehensive computational study of aza-Michael addition of pyrrolidine to methyl acrylate catalyzed by dihalogen molecules (X2), namely, F2, Cl2, Br2 and I2 [49]. All geometries were optimized and characterized at the M06-2X/def2-TZVP level. Scalar relativistic effects were accounted for using the zeroth-order regular approximation (ZORA) [85,86]. DLPNO-CCSD(T) calculations were performed using the def2-TZVP basis set on M06-2X/def2-TZVP geometries.
The authors calculated the four dihalogen molecule-catalyzed reactions at the M06-2X/def2-TZVP level and compared them to the uncatalyzed reaction (Figure 10) [49]. They observed a systematic decrease of the reaction barrier down Group 17, from 9.4 kcal/mol for F2 to 5.7 kcal/mol for I2. In comparison, the uncatalyzed reaction has an activation barrier of 11.2 kcal/mol. Correspondingly, the TSs are reached earlier and the formed C–N bonds are longer going down the group. Overlaid TSs (Figure 10) clearly show a systematic change of the TS structures. These observed trends are consistent with the experimental observation of the trend of activity within the halogen group.
The activation of substrates by XB interaction was commonly thought to originate from lowering the LUMO energies of the electrophiles and, hence, stronger HOMO (nucleophile)–LUMO (electrophile) interaction. Indeed, a good correlation (R2 = 0.97) was obtained between reaction barriers and HOMO–LUMO gaps (Figure 11). However, when the interaction was analyzed using the activation strain model (ASM) [87], the authors found unexpectedly that the physical factor controlling the computed reactivity trend is not the abovementioned enhanced donor–acceptor interaction, but rather a diminished Pauli repulsion between the lone pair of the nucleophile pyrrolidine and the Michael acceptor’s π-electron system. We refer interested readers to the original paper [49] for more in-depth discussion of the energy decomposition analysis, which is beyond the scope of the current review.
Understanding the origin of halogen bond activation is important in many aspects of XB catalysis, particularly the design of new catalysts. Thus, this new view could potentially change the way we understand XB catalysis and design new XB catalysts. However, several aspects of the computation need further improvement, which is discussed below, and the usefulness of the new interpretation in predicting catalyst activity needs corroboration from other studies.
The molecular structures used in the ASM energy analyses were optimized in the gas phase, which is not ideal for the nucleophilic addition reaction studied here since the addition product is a zwitterionic intermediate. In comparison, Breugst and co-workers reported a very different free energy reaction profile for the same I2-catalyzed Michael addition reaction, calculated using the SMD solvent model [81], from the one presented in Figure 10. For example, in Figure 10, I2-INT has the same energy as I2-TS, ΔG298 = 19.2 kcal/mol, whereas Breugst calculated an energy difference of 6.5 kcal/mol for the same two species in the presence of dichloromethane solvent. Unless the solvent effect is considered, which is certainly critical for accurate geometries and energies for catalytic reactions happening in solution, the gas-phase analysis might have limited relevance to experimental XB catalysis.
Similar to the I2-catalyzed iso-Nazarov cyclization reaction discussed in Section 3.2.4, reaction barriers were calculated with reference to the halogen bonded complexes. This could lead to potential bias toward catalyzed reactions. Furthermore, we are yet to see experimental studies employing F2 or Cl2 as a catalyst in organic reactions that involve reactive compounds such as pyrrolidine.

3.2.6. XB in Metal Acetate-Catalyzed Halolactonization

The above examples are computational studies of neutral XB-catalyzed reactions. There are many literature reports of halogenation reactions where, prior to the halogenation step, halogen bonds are formed between some Lewis base and the halogenation agents [88,89,90]. Such XBs are transient in nature, as the X–A (X is the halogen and A is some heteroatom) bonds are cleaved in TSs. Recently, Arai and co-workers reported a metal acetate-catalyzed asymmetric halolactonization, where halogen bonding interaction was proposed as a key secondary interaction in the transition state [91]. Experimentally, the authors found that molecular iodine has a significant impact on the acceleration of the reaction. In their computational study, two TS models were proposed, Model-A and Model-B (Scheme 3). In Model-A, iodination of the double bond occurs directly from N-iodosuccinimide (NIS), whereas, in Model-B, it is from I2, which simultaneously forms a key XB with NIS. Calculated results showed that the Model-B TS is 12.6 kcal/mol lower in energy than the corresponding Model-A TS, in good agreement with experiments. Molecular iodine and NIS are reactive reagents, and each is susceptible to several plausible reaction pathways. It will require further careful mechanistic studies considering different reaction pathways to confirm the role of XB in this reaction.

3.3. Cationic XB Catalysts

Over the past decade, advancements of XB catalysis were largely centered on cationic iodine-containing catalysts based on nitrogen heterocycle scaffolds, e.g., imidazoliniums, imidazoliums, and triazoliums, which were reported to catalyze a variety of organic transformations.

3.3.1. XB-Catalyzed Reduction of Quinolines by Hantzsch Ester

Reduction of quinoline by Hantzsch ester is an important organic reaction that was explored many times in the literature as a benchmark reaction for new XB catalysts [16,21,26]. In 2014, Tan et al. reported that iodoimidazolinium compound (39) (Scheme 4) can catalyze the reduction of quinoline by Hantzsch ester to give 91% yield in dichloromethane at room temperature. Interestingly, a related iodoimidazolium catalyst (40) gave only a trace amount of product yield. Recently, our group reported a comprehensive computational mechanistic study of the reaction at the M06-2X/6-311+G(d,p)(def2-TZVPD for iodine)//M06-2X/6-31G(d)(def2-SVP for iodine) level, with the SMD solvent model and SMD18 correction [43]. For all calculations involving 39 and 40, the triflate anion was included to neutralize the catalytic systems.
Similarly, the mechanism of the XB-catalyzed reaction pathway was investigated. The lowest energy pathway is presented in Figure 12 and compared to the uncatalyzed pathway. One major finding is that it is preferable for the iodine atom of 39 to bind to the deprotonated nitrogen atom of Hantzsch ester in the key hydride transfer transition states, namely, 39-TS2-XB and 39-TS4-XB, instead of the nitrogen atom of quinoline [21]. Compared to the uncatalyzed reactions, XBs lower the reaction free energy barriers of hydride transfer steps by about 5 kcal/mol. However, they do not appreciably lower the barriers of the proton transfer steps.
More significantly, the report is the first one of which we are aware that discovered a Brønsted acid pathway (Figure 13) that was predicted to be competitive to the hypothesized XB catalysis. Hantzsch ester, being a reductant, can reduce the charged iodoimidazolinium moiety of 39 to generate a Brønsted acid with a relatively low barrier of 26.8 kcal/mol, which is lower than that of the first transition state of the XB catalysis pathway (28.8 kcal/mol). Following the generation of acid catalyst, the reduction can be catalyzed very efficiently. In comparison, when reduction of 40 by Hantzsch ester was calculated, the barrier was higher at 33.4 kcal/mol, reflecting the aromatic nature of the imidazolium core of 40. The result is in good agreement with the experimental finding where 40 failed to catalyze the reaction (Scheme 4).
This computational study highlights the necessity and challenges of comparing XB to other possible pathways, particularly the Brønsted acid catalysis pathway. Unlike the XB pathway, the Brønsted acid pathway requires the acid to be generated before the catalysis initiates, which may be accomplished in many unexpected ways and from many overlooked sources. Future computational mechanistic studies should take precaution to avoid too narrow a consideration of the Brønsted acid pathway in favor of the XB pathway. The view is echoed by a recent experimental report of the Scheidt group [28], who discovered through control studies that, for cationic XB catalysts, the activity may stem from a trace amount of Brønsted acid produced from adventitious water.

3.3.2. XB-Catalyzed Conjugate Addition of Thiophenes to Enones and Enals

Tan et al. reported an XB-catalyzed conjugate addition of thiophenes to enones and enals [92]. A bidentate imidazolinium-based catalyst (47) was found to be the most active catalysts tested. The mechanism of this reaction was investigated by our group using the MN15 functional. The solvent effect was modeled with the SMD method and dichloroethane (DCE) was used as the solvent. Relative free energies at 298 K (ΔG298) were reported (Figure 14).
The catalyzed reaction was firstly investigated and it was found to be an asynchronous concerted reaction. The C–C bond formation was immediately followed by a proton transfer, yielding an enol intermediate (45), which readily tautomerizes to give the final addition product (46). The reaction barrier was calculated to be very high at 40.4 kcal/mol, in accordance with experiment that the reaction does not occur without a catalyst.
In comparison, catalysis by 47 through a pincer type XB binding to the enone substrate changes the reaction mechanism to follow a stepwise pathway (Figure 14). A stable intermediate, 43-INT-XB, in which catalyst 47 forms two strong XBs to the negatively charged enolate, at 2.51 and 2.49 Å, could be located at a reasonable energy level of 22.1 kcal/mol. The magnitude of XB stabilization in this intermediate was estimated through a distortion-interaction model, assuming the interaction comes mainly from the XBs. A large stabilization energy of 37.8 kcal/mol was calculated and found to be the largest along the reaction profile. This magnitude of stabilization is more than enough to compensate for the entropy loss of forming two XBs simultaneously, which is typically beyond the reach of monodentate XB catalysts except perhaps the strongest ones. The rate-limiting step of the catalyzed reaction was determined to be the first C–C bond-formation step. The reaction free energy barrier was reduced by 12.8 kcal/mol to 27.6 kcal/mol when compared to the uncatalyzed reaction.
The competing Brønsted acid pathway was not investigated computationally. Instead, the experimental result in the same study showed that, in the presence of Cs2CO3 base, the yield of 46 decreased from 88% to 56%, indicating that a substantial portion of the reaction might go through the Brønsted acid catalysis pathway. However, the source and mechanism of the acid catalyst generation is still unclear.

3.3.3. Catalysis by C–I···π Type of XB Interaction

Unlike most reported studies of XB catalysis, in which the halogen atoms bind to lone pairs of some heteroatoms, Arai et al. very recently reported the first catalyzed [4+2] cycloaddition whose substrate was proposed to be activated through C–I···π interaction [93]. Calculations done at the M06-2X/6-31G(d) (LANL2DZdp for iodine atoms) level showed that the C–I···π complex between a cationic XB donor (48) and 2-alkenylindole (49) was 2.3 kcal/mol lower in energy than the π···π complex, which was attributed to the destabilization effect of phenyl moieties of the XB catalyst (Figure 15).
When the TS catalyzed by C–I···π interaction, namely, 49-TS-XB-Syn, was compared to the uncatalyzed TS, 49-TS-UN, the reaction free energy barrier was reduced significantly by 5.4 kcal/mol. Calculations also revealed that the π···π interaction-catalyzed TS, 49-TS-ππ, was slightly higher in energy, with a reaction barrier of 25.5 kcal/mol (Figure 16). Overall, there is a good agreement between the calculated diastereoselectivity, ΔΔG≠ = 0.7 kcal/mol between the anti and syn TSs, and the experimental results.
The claim of the C–I···π type of XB interaction being able to catalyze an organic reaction in preference to other well-established interactions seems quite promising and may in time lead to more discovery of XB-catalyzed reactions. However, given the scarcity of the reported difference between complexes and TSs of different activation modes, further investigation is needed to establish the C–I···π interaction unambiguously as a new type of XB activation.

3.4. Hypervalent Iodine(III)-Catalyzed Reactions

ICl3-Catalyzed Ring-Opening Polymerization of l-Lactide

Hypervalent iodine(III) compounds are versatile reagents that are used in many organic reactions. The high oxidation state of +3 renders them electrophilic. Therefore, they are able to interact with lone pairs of electronegative atoms to form noncovalent XBs. One of the earliest reports of XB catalysis is the ICl3-catalyzed ring-opening polymerization of l-lactide by Coulembier et al. [57]. In 2019, Zeng et al. reported a computational study of the mechanism of this reaction [94].
Two different pathways, concerted and stepwise, together with the corresponding catalyzed pathways, were investigated at the PBE0/6-311+G(d,p) (aug-cc-pVDZ-PP for iodine) level, and the results are summarized in Figure 17. All calculated pathways have substantially high activation barriers of more than 35 kcal/mol. A third pathway, in which the ICl3 catalyst forms covalent bonds with l-lactide instead of through noncovalent XB, was calculated to be more favorable compared to XB-catalysis pathways.
The apparent high barriers of the XB pathways, notwithstanding the exclusion of the entropic component which could further add to the reaction barriers, indicate that other mechanistic pathways other than the reported four-membered ring TSs might be in operation. Furthermore, as noted above, hypervalent iodine(III) compounds are often used as reagents instead of catalysts. In the presence of an alcohol reagent 54, the possibility of Brønsted acid generation should be thoroughly investigated and compared to the XB catalysis pathway.

4. Summary and Outlook

Halogen bonding is now established clearly as a reliable noncovalent motif in organocatalysis. We witnessed a continued progress in the application of XB to organocatalysis in recent years. Although computational mechanistic studies of reactions catalyzed by halogen-containing catalysts are still very few, there seems to now be sufficient computational evidence in support of the possibility of XB activation in organocatalysis. Calculated TS structures reported in the literature showed that the catalysts employed can activate substrates through interaction at the halogen site, with features characteristic of a typical halogen bond, e.g., close to linear binding angle and less than the sum of van der Waals radii binding distance. Various energy decomposition analyses of the strength of XB binding seem to indicate that it could be strong enough to attain a lowering of the reaction free energy barrier.
To provide stronger support for the XB activation mode through computational studies, several practices are recommended in future studies. Firstly, the entropic contribution to reaction barrier, if possible, should be included, or at least assessed in some empirical ways when it is difficult to calculate. Failing to include it may result in overestimation of XB activation with respect to the uncatalyzed reaction and poor agreement with experiments. Secondly, for cationic halogen bond catalysts, the effect of counter anions on the reaction barriers needs to be examined. It is common practice to omit them when calculating catalyzed transition states, assuming they have a minimal effect. Experimentally, there is evidence that the effect may not be as minimal as once thought. On the other hand, calculated reaction free energy barriers are sometimes rather close to those of uncatalyzed reactions. Thirdly, comparison to other possible pathways is highly desirable, especially to the Brønsted acid pathway. It was noted experimentally and theoretically by Breugst et al. [81], Scheidt et al. [28], and our group [43,92] that the Brønsted acid catalysis pathway is competitive or superior to the XB catalysis pathway for the investigated reactions. However, the understanding of how a trace amount of acid could be generated is quite limited, perhaps because there are not many experimental reports, if any, of such a nature. Further computational studies founded on more extensive evidence are needed. Finally, a whole reaction profile, detailing every elementary step, is necessary to understand the reaction kinetics, to which, corresponding experimental data, e.g., reaction orders and kinetic isotope effects, could be directly compared (if they exist).
Computational studies could also help to advance this growing field through screening new catalysts before experimental synthesis of selected top candidates. The experimental design of new and novel XB catalysts is always highly sought after but very challenging, owing to the fact that, to overcome the unfavorable entropy penalty, it is usually necessary to form multiple halogen bonding interactions with the substrates. Furthermore, XB is highly directional and usually weaker than the corresponding hydrogen bond, and design of multidentate XB catalysts to achieve close-to-optimal binding in key transition states poses a very strict requirement on molecular geometry. Moreover, the atom σ-bonded to the halogen atoms is currently restricted only to carbon, while other atoms like nitrogen and oxygen, which are commonly found in hydrogen bond catalysis, will render the σ bond liable to homolysis or other reaction channels.
On the other hand, the computational design of new halogen bond catalysts can benefit from the speed of computational design relative to actual synthesis and experimental testing of designed catalysts, which is both challenging and tedious. More importantly, it seems quite plausible that computational design could also benefit from design strategies already well developed in the field of de novo drug design. The quest for a scaffold or linker connecting isolated halogen bond donors to achieve maximal catalyst–substrate interaction parallels well to computer-aided drug discovery. Reports of such an approach might be expected in the near future. Thus, we believe that in silico design will play a very important role in designing the right catalyst with optimal halogen bonding interactions with the substrate.
Lastly, asymmetric catalysis utilizing halogen bond as a control element is starting to appear in literature [95]. We expect that many more papers may appear, and the strategy may mature to a standard protocol in organocatalysis. We certainly will see more contribution by the computational chemistry community in this respect. In summary, theoretical studies will continue to play critical roles in the mechanistic understanding and design of next-generation novel XB-based organocatalysts.

Supplementary Materials

The following are available online, Table S1: Cartesian coordinates (Å), thermodynamics of the optimized structures at DFT/6-31G+(d)+def2-SVP(I) level, and single point energies at DFT/6-311++G(2d,p)+def2-TZVPD(I)level.

Author Contributions

Conceptualization, H.Y. and M.W.W.; formal analysis, H.Y. and M.W.W.; investigation, H.Y. and M.W.W.; writing—original draft preparation, H.Y. and M.W.W.; writing—review and editing, H.Y. and M.W.W.; funding acquisition, M.W.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Education (Singapore), MOE2016-T2-1-087.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
  3. Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. Proceedings of “Modeling interactions in biomolecules II”, Prague, September 5th-9th, 2005. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef]
  4. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
  5. Ang, S.J.; Mak, A.M.; Sullivan, M.B.; Wong, M.W. Site specificity of halogen bonding involving aromatic acceptors. Phys. Chem. Chem. Phys. 2018, 20, 8685–8694. [Google Scholar] [CrossRef] [PubMed]
  6. Angarov, V.; Kozuch, S. On the σ, π and δ hole interactions: A molecular orbital overview. New J. Chem. 2018, 42, 1413–1422. [Google Scholar] [CrossRef]
  7. Wolters, L.P.; Bickelhaupt, F.M. Halogen bonding versus hydrogen bonding: A molecular orbital perspective. ChemistryOpen 2012, 1, 96–105. [Google Scholar] [CrossRef]
  8. Ang, S.J.; Mak, A.M.; Wong, M.W. Nature of halogen bonding involving π-systems, nitroxide radicals and carbenes: A highlight of the importance of charge transfer. Phys. Chem. Chem. Phys. 2018, 20, 26463–26478. [Google Scholar] [CrossRef]
  9. Thirman, J.; Engelage, E.; Huber, S.M.; Head-Gordon, M. Characterizing the interplay of Pauli repulsion, electrostatics, dispersion and charge transfer in halogen bonding with energy decomposition analysis. Phys. Chem. Chem. Phys. 2018, 20, 905–915. [Google Scholar] [CrossRef]
  10. Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On the nature of the halogen bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef]
  11. Robinson, S.W.; Mustoe, C.L.; White, N.G.; Brown, A.; Thompson, A.L.; Kennepohl, P.; Beer, P.D. Evidence for halogen bond covalency in acyclic and interlocked halogen-bonding receptor anion recognition. J. Am. Chem. Soc. 2015, 137, 499–507. [Google Scholar] [CrossRef]
  12. Mustoe, C.L.; Gunabalasingam, M.; Yu, D.; Patrick, B.O.; Kennepohl, P. Probing covalency in halogen bonds through donor K-edge X-ray absorption spectroscopy: Polyhalides as coordination complexes. Faraday Discuss. 2017, 203, 79–91. [Google Scholar] [CrossRef]
  13. Erakovic, M.; Cincic, D.; Molcanov, K.; Stilinovic, V. A crystallographic charge density study of the partial covalent nature of strong NBr halogen bonds. Angew. Chem. Int. Ed. 2019, 58, 15702–15706. [Google Scholar] [CrossRef]
  14. Grabowski, S.J. Hydrogen and halogen bonds are ruled by the same mechanisms. Phys. Chem. Chem. Phys. 2013, 15, 7249–7259. [Google Scholar] [CrossRef]
  15. Politzer, P.; Murray, J.S.; Lane, P. σ-Hole bonding and hydrogen bonding: Competitive interactions. Int. J. Quantum Chem. 2007, 107, 3046–3052. [Google Scholar] [CrossRef]
  16. Bolm, C.; Bruckmann, A.; Pena, M. Organocatalysis through halogen-bond activation. Synlett 2008, 2008, 900–902. [Google Scholar] [CrossRef]
  17. Bulfield, D.; Huber, S.M. Halogen bonding in organic synthesis and organocatalysis. Chem. Eur. J. 2016, 22, 14434–14450. [Google Scholar] [CrossRef]
  18. Sutar, R.L.; Huber, S.M. Catalysis of organic reactions through halogen bonding. ACS Catal. 2019, 9, 9622–9639. [Google Scholar] [CrossRef]
  19. Walter, S.M.; Kniep, F.; Herdtweck, E.; Huber, S.M. Halogen-bond-induced activation of a carbon–heteroatom bond. Angew. Chem. Int. Ed. 2011, 50, 7187–7191. [Google Scholar] [CrossRef]
  20. Kniep, F.; Jungbauer, S.H.; Zhang, Q.; Walter, S.M.; Schindler, S.; Schnapperelle, I.; Herdtweck, E.; Huber, S.M. Organocatalysis by neutral multidentate halogen-bond donors. Angew. Chem. Int. Ed. 2013, 52, 7028–7032. [Google Scholar] [CrossRef]
  21. He, W.; Ge, Y.C.; Tan, C.H. Halogen-bonding-induced hydrogen transfer to C=N bond with Hantzsch ester. Org. Lett. 2014, 16, 3244–3247. [Google Scholar] [CrossRef]
  22. Jungbauer, S.H.; Bulfield, D.; Kniep, F.; Lehmann, C.W.; Herdtweck, E.; Huber, S.M. Toward molecular recognition: Three-point halogen bonding in the solid state and in solution. J. Am. Chem. Soc. 2014, 136, 16740–16743. [Google Scholar] [CrossRef]
  23. Jungbauer, S.H.; Huber, S.M. Cationic multidentate halogen-bond donors in halide abstraction organocatalysis: Catalyst optimization by preorganization. J. Am. Chem. Soc. 2015, 137, 12110–12120. [Google Scholar] [CrossRef]
  24. Bergamaschi, G.; Lascialfari, L.; Pizzi, A.; Martinez Espinoza, M.I.; Demitri, N.; Milani, A.; Gori, A.; Metrangolo, P. A halogen bond-donor amino acid for organocatalysis in water. Chem. Commun. 2018, 54, 10718–10721. [Google Scholar] [CrossRef]
  25. Dreger, A.; Engelage, E.; Mallick, B.; Beer, P.D.; Huber, S.M. The role of charge in 1,2,3-triazol(ium)-based halogen bonding activators. Chem. Commun. 2018, 54, 4013–4016. [Google Scholar] [CrossRef] [Green Version]
  26. Matsuzaki, K.; Uno, H.; Tokunaga, E.; Shibata, N. Fluorobissulfonylmethyl iodides: An efficient scaffold for halogen bonding catalysts with an sp3-hybridized carbon–iodine moiety. ACS Catal. 2018, 8, 6601–6605. [Google Scholar] [CrossRef]
  27. Schulz, N.; Sokkar, P.; Engelage, E.; Schindler, S.; Erdelyi, M.; Sanchez-Garcia, E.; Huber, S.M. The interaction modes of haloimidazolium salts in solution. Chem. Eur. J. 2018, 24, 3464–3473. [Google Scholar] [CrossRef]
  28. Squitieri, R.A.; Fitzpatrick, K.P.; Jaworski, A.A.; Scheidt, K.A. Synthesis and evaluation of azolium-based halogen-bond donors. Chem. Eur. J. 2019, 25, 10069–10073. [Google Scholar] [CrossRef]
  29. Szell, P.M.J.; Zablotny, S.; Bryce, D.L. Halogen bonding as a supramolecular dynamics catalyst. Nat. Commun. 2019, 10, 916. [Google Scholar] [CrossRef] [Green Version]
  30. Erdélyi, M. Halogen bonding in solution. Chem. Soc. Rev. 2012, 41, 3547–3557. [Google Scholar]
  31. Beale, T.M.; Chudzinski, M.G.; Sarwar, M.G.; Taylor, M.S. Halogen bonding in solution: Thermodynamics and applications. Chem. Soc. Rev. 2013, 42, 1667–1680. [Google Scholar] [CrossRef]
  32. Walter, S.M.; Kniep, F.; Rout, L.; Schmidtchen, F.P.; Herdtweck, E.; Huber, S.M. Isothermal calorimetric titrations on charge-assisted halogen bonds: Role of entropy, counterions, solvent, and temperature. J. Am. Chem. Soc. 2012, 134, 8507–8512. [Google Scholar] [CrossRef]
  33. Von der Heiden, D.; Bozkus, S.; Klussmann, M.; Breugst, M. Reaction mechanism of iodine-catalyzed Michael additions. J. Org. Chem. 2017, 82, 4037–4043. [Google Scholar] [CrossRef]
  34. Chan, Y.C.; Yeung, Y.Y. Halogen-bond-catalyzed addition of carbon-based nucleophiles to N-acylimminium ions. Org. Lett. 2019, 21, 5665–5669. [Google Scholar] [CrossRef]
  35. Purvis, G.D.; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  36. Kozuch, S.; Martin, J.M.L. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef]
  37. Kesharwani, M.K.; Manna, D.; Sylvetsky, N.; Martin, J.M.L. The X40 × 10 halogen bonding benchmark revisited: Surprising importance of (n-1)d subvalence correlation. J. Phys. Chem. A 2018, 122, 2184–2197. [Google Scholar] [CrossRef]
  38. Anderson, L.N.; Aquino, F.W.; Raeber, A.E.; Chen, X.; Wong, B.M. Halogen bonding interactions: Revised benchmarks and a new assessment of exchange vs. dispersion. J. Chem. Theory Comput. 2018, 14, 180–190. [Google Scholar] [CrossRef] [Green Version]
  39. Ang, S.J.; Ser, C.T.; Wong, M.W. Modeling halogen bonding with planewave density functional theory: Accuracy and challenges. J. Comput. Chem. 2019, 40, 1829–1835. [Google Scholar] [CrossRef]
  40. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  41. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
  42. Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn-Sham global-hybrid exchange-correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [Green Version]
  43. Ser, C.T.; Yang, H.; Wong, M.W. Iodoimidazolinium-catalyzed reduction of quinoline by Hantzsch ester: Halogen bond or Brønsted acid catalysis. J. Org. Chem. 2019, 84, 10338–10348. [Google Scholar] [CrossRef] [Green Version]
  44. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
  45. Engelage, E.; Schulz, N.; Heinen, F.; Huber, S.M.; Truhlar, D.G.; Cramer, C.J. Refined SMD parameters for bromine and iodine accurately model halogen-bonding interactions in solution. Chem. Eur. J. 2018, 24, 15983–15987. [Google Scholar] [CrossRef]
  46. Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef]
  47. Yepes, D.; Neese, F.; List, B.; Bistoni, G. Unveiling the delicate balance of steric and dispersion interactions in organocatalysis using high-level computational methods. J. Am. Chem. Soc. 2020, 142, 3613–3625. [Google Scholar] [CrossRef] [Green Version]
  48. Liakos, D.G.; Neese, F. Is it possible to obtain coupled cluster quality energies at near density functional theory cost? Domain-based local pair natural orbital coupled cluster vs. modern density functional theory. J. Chem. Theory Comput. 2015, 11, 4054–4063. [Google Scholar] [CrossRef]
  49. Hamlin, T.A.; Fernandez, I.; Bickelhaupt, F.M. How dihalogens catalyze Michael addition reactions. Angew. Chem. Int. Ed. 2019, 58, 8922–8926. [Google Scholar] [CrossRef] [Green Version]
  50. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
  51. Sarwar, M.G.; Dragisic, B.; Salsberg, L.J.; Gouliaras, C.; Taylor, M.S. Thermodynamics of halogen bonding in solution: Substituent, structural, and solvent effects. J. Am. Chem. Soc. 2010, 132, 1646–1653. [Google Scholar] [CrossRef] [PubMed]
  52. Jungbauer, S.H.; Walter, S.M.; Schindler, S.; Rout, L.; Kniep, F.; Huber, S.M. Activation of a carbonyl compound by halogen bonding. Chem. Commun. 2014, 50, 6281–6284. [Google Scholar] [CrossRef] [PubMed]
  53. Gliese, J.P.; Jungbauer, S.H.; Huber, S.M. A halogen-bonding-catalyzed Michael addition reaction. Chem. Commun. 2017, 53, 12052–12055. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  54. Dreger, A.; Wonner, P.; Engelage, E.; Walter, S.M.; Stoll, R.; Huber, S.M. A halogen-bonding-catalysed Nazarov cyclisation reaction. Chem. Commun. 2019, 55, 8262–8265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  55. Stoesser, J.; Rojas, G.; Bulfield, D.; Hidalgo, P.I.; Pasán, J.; Ruiz-Pérez, C.; Jiménez, C.A.; Huber, S.M. Halogen bonding two-point recognition with terphenyl derivatives. New J. Chem. 2018, 42, 10476–10480. [Google Scholar] [CrossRef]
  56. Linke, A.; Jungbauer, S.H.; Huber, S.M.; Waldvogel, S.R. Potent affinity material for tracing acetone and related analytes based on molecular recognition by halogen bonds. Chem. Commun. 2015, 51, 2040–2043. [Google Scholar] [CrossRef] [Green Version]
  57. Coulembier, O.; Meyer, F.; Dubois, P. Controlled room temperature ROP of L-lactide by ICl3: A simple halogen-bonding catalyst. Polym. Chem. 2010, 1, 434–437. [Google Scholar] [CrossRef]
  58. Chan, Y.C.; Yeung, Y.Y. Halogen bond catalyzed bromocarbocyclization. Angew. Chem. Int. Ed. 2018, 57, 3483–3487. [Google Scholar] [CrossRef]
  59. Togo, H.; Iida, S. Synthetic use of molecular iodine for organic synthesis. Synlett 2006, 2006, 2159–2175. [Google Scholar] [CrossRef]
  60. Thakur, A.; Das, S.; Borah, R.; Devi, R. Molecular iodine in protection and deprotection chemistry. Synlett 2008, 2008, 2741–2762. [Google Scholar] [CrossRef]
  61. Jereb, M.; Vražič, D.; Zupan, M. Iodine-catalyzed transformation of molecules containing oxygen functional groups. Tetrahedron 2011, 67, 1355–1387. [Google Scholar] [CrossRef]
  62. Parvatkar, P.T.; Parameswaran, P.S.; Tilve, S.G. Recent developments in the synthesis of five- and six-membered heterocycles using molecular iodine. Chem. Eur. J. 2012, 18, 5460–5489. [Google Scholar] [CrossRef] [PubMed]
  63. Ren, Y.-M.; Cai, C.; Yang, R.-C. Molecular iodine-catalyzed multicomponent reactions: An efficient catalyst for organic synthesis. RSC Adv. 2013, 3, 7182–7204. [Google Scholar] [CrossRef]
  64. Breugst, M.; von der Heiden, D. Mechanisms in iodine catalysis. Chem. Eur. J. 2018, 24, 9187–9199. [Google Scholar] [CrossRef]
  65. Hibbert, H. Use of iodine as a dehydrating and condensing agent. J. Am. Chem. Soc. 1915, 37, 1748–1763. [Google Scholar] [CrossRef] [Green Version]
  66. Heinen, F.; Engelage, E.; Dreger, A.; Weiss, R.; Huber, S.M. Iodine(III) derivatives as halogen bonding organocatalysts. Angew. Chem. Int. Ed. 2018, 57, 3830–3833. [Google Scholar] [CrossRef]
  67. Corey, E.J.; Grogan, M.J. Enantioselective synthesis of α-amino nitriles from N-benzhydryl imines and HCN with a chiral bicyclic guanidine as catalyst. Org. Lett. 1999, 1, 157–160. [Google Scholar] [CrossRef]
  68. Heinz, N.; Dolg, M.; Berkessel, A. A theoretical study of imine hydrocyanation catalyzed by halogen-bonding. J. Comput. Chem. 2015, 36, 1812–1817. [Google Scholar] [CrossRef]
  69. Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
  70. Matsuzawa, A.; Takeuchi, S.; Sugita, K. Iodoalkyne-based catalyst-mediated activation of thioamides through halogen bonding. Chem. Asian J. 2016, 11, 2863–2866. [Google Scholar] [CrossRef]
  71. Kee, C.W.; Wong, M.W. In silico design of halogen-bonding-based organocatalyst for Diels–Alder reaction, Claisen rearrangement, and Cope-type hydroamination. J. Org. Chem. 2016, 81, 7459–7470. [Google Scholar] [CrossRef] [PubMed]
  72. Kozuch, S.; Shaik, S. A combined kinetic−quantum mechanical model for assessment of catalytic cycles:  Application to cross-coupling and Heck reactions. J. Am. Chem. Soc. 2006, 128, 3355–3365. [Google Scholar] [CrossRef] [PubMed]
  73. Kozuch, S.; Shaik, S. How to conceptualize catalytic cycles? The energetic span model. Acc. Chem. Res. 2011, 44, 101–110. [Google Scholar] [CrossRef]
  74. Uhe, A.; Kozuch, S.; Shaik, S. Automatic analysis of computed catalytic cycles. J. Comput. Chem. 2011, 32, 978–985. [Google Scholar] [CrossRef]
  75. Mitsumori, S.; Zhang, H.; Ha-Yeon Cheong, P.; Houk, K.N.; Tanaka, F.; Barbas, C.F. Direct asymmetric anti-Mannich-type reactions catalyzed by a designed amino acid. J. Am. Chem. Soc. 2006, 128, 1040–1041. [Google Scholar] [CrossRef] [PubMed]
  76. Shinisha, C.B.; Sunoj, R.B. Bicyclic proline analogues as organocatalysts for stereoselective aldol reactions: An in silico DFT study. Org. Biomol. Chem. 2007, 5, 1287–1294. [Google Scholar] [CrossRef] [PubMed]
  77. Malerich, J.P.; Hagihara, K.; Rawal, V.H. Chiral squaramide derivatives are excellent hydrogen bond donor catalysts. J. Am. Chem. Soc. 2008, 130, 14416–14417. [Google Scholar] [CrossRef] [Green Version]
  78. Neel, A.J.; Hehn, J.P.; Tripet, P.F.; Toste, F.D. Asymmetric cross-dehydrogenative coupling enabled by the design and application of chiral triazole-containing phosphoric acids. J. Am. Chem. Soc. 2013, 135, 14044–14047. [Google Scholar] [CrossRef] [Green Version]
  79. Markad, D.; Mandal, S.K. Design of a primary-amide-functionalized highly efficient and recyclable hydrogen-bond-donating heterogeneous catalyst for the Friedel–Crafts alkylation of indoles with β-nitrostyrenes. ACS Catal. 2019, 9, 3165–3173. [Google Scholar] [CrossRef]
  80. Yang, H.; Wong, M.W. b-amino acid catalyzed asymmetric Michael additions: Design of organocatalysts with catalytic acid/base dyad inspired by serine proteases. J. Org. Chem. 2011, 76, 7399–7405. [Google Scholar] [CrossRef]
  81. Breugst, M.; Detmar, E.; von der Heiden, D. Origin of the catalytic effects of molecular iodine: A computational analysis. ACS Catal. 2016, 6, 3203–3212. [Google Scholar] [CrossRef]
  82. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  83. Marsili, L.A.; Pergomet, J.L.; Gandon, V.; Riveira, M.J. Iodine-catalyzed iso-Nazarov cyclization of conjugated dienals for the synthesis of 2-cyclopentenones. Org. Lett. 2018, 20, 7298–7303. [Google Scholar] [CrossRef]
  84. Koenig, J.J.; Arndt, T.; Gildemeister, N.; Neudorfl, J.M.; Breugst, M. Iodine-catalyzed Nazarov cyclizations. J. Org. Chem. 2019, 84, 7587–7605. [Google Scholar] [CrossRef]
  85. Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
  86. Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
  87. Van Zeist, W.J.; Bickelhaupt, F.M. The activation strain model of chemical reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. [Google Scholar] [CrossRef]
  88. Denmark, S.E.; Kuester, W.E.; Burk, M.T. Catalytic, asymmetric halofunctionalization of alkenes—A critical perspective. Angew. Chem. Int. Ed. 2012, 51, 10938–10953. [Google Scholar] [CrossRef] [Green Version]
  89. Cheng, Y.A.; Yu, W.Z.; Yeung, Y.-Y. Recent advances in asymmetric intra- and intermolecular halofunctionalizations of alkenes. Org. Biomol. Chem. 2014, 12, 2333–2343. [Google Scholar] [CrossRef]
  90. Guha, S.; Kazi, I.; Nandy, A.; Sekar, G. Role of Lewis-base-coordinated halogen(I) intermediates in organic synthesis: The journey from unstable intermediates to versatile reagents. Eur. J. Org. Chem. 2017, 2017, 5497–5518. [Google Scholar] [CrossRef]
  91. Arai, T.; Horigane, K.; Watanabe, O.; Kakino, J.; Sugiyama, N.; Makino, H.; Kamei, Y.; Yabe, S.; Yamanaka, M. Association of halogen bonding and hydrogen bonding in metal acetate-catalyzed asymmetric halolactonization. iScience 2019, 12, 280–292. [Google Scholar] [CrossRef] [PubMed]
  92. Ge, Y.-C.; Yang, H.; Heusler, A.; Chua, Z.; Wong, M.W.; Tan, C.-H. Halogen-bonding-induced conjugate addition of thiophenes to enones and enals. Chem. Asian J. 2019, 14, 2656–2661. [Google Scholar] [CrossRef] [PubMed]
  93. Kuwano, S.; Suzuki, T.; Yamanaka, M.; Tsutsumi, R.; Arai, T. Catalysis based on C−I⋅⋅⋅π halogen bonds: Electrophilic activation of 2-alkenylindoles by cationic halogen-bond donors for [4+2] cycloadditions. Angew. Chem. Int. Ed. 2019, 58, 10220–10224. [Google Scholar] [CrossRef] [PubMed]
  94. Guo, S.; Sun, C.; Meng, L.; Zeng, Y. The mechanism of ring-opening polymerization of L-lactide by ICl3 catalysts: Halogen bond catalysis or participating in reactions? J. Comput. Chem. 2019, 40, 2827–2833. [Google Scholar] [CrossRef]
  95. Sutar, R.L.; Engelage, E.; Stoll, R.; Huber, S.M. Bidentate chiral bis(imidazolium)-based halogen bond donors: Synthesis and first applications in enantioselective recognition and catalysis. Angew. Chem. Int. Ed. 2020. [Google Scholar] [CrossRef] [Green Version]
Molecules 25 01045 g001 550
Figure 1. (a) Electrostatic (σ-hole) and (b) molecular orbital models of halogen bond (XB) formation. The formation of an XB complex between CF3I (XB-donor) and H2O (XB-acceptor) is used as an illustration.
Figure 1. (a) Electrostatic (σ-hole) and (b) molecular orbital models of halogen bond (XB) formation. The formation of an XB complex between CF3I (XB-donor) and H2O (XB-acceptor) is used as an illustration.
Molecules 25 01045 g001
Molecules 25 01045 sch001 550
Scheme 1. Perfluoroidoalkane (5)-catalyzed reduction of quinolines (1) by Hantzsch ester (2).
Scheme 1. Perfluoroidoalkane (5)-catalyzed reduction of quinolines (1) by Hantzsch ester (2).
Molecules 25 01045 sch001
Molecules 25 01045 g002 550
Figure 2. Calculated transition states for halogen bond-catalyzed (a) Diels–Alder cycloaddition [52], (b) Michael addition of indole to trans-crotonophenone [53], and (c) Nazarov cyclization reaction [54]. XB distances are in Å and A–I···B angles are in degrees. Hydrogen atoms are omitted for clarity.
Figure 2. Calculated transition states for halogen bond-catalyzed (a) Diels–Alder cycloaddition [52], (b) Michael addition of indole to trans-crotonophenone [53], and (c) Nazarov cyclization reaction [54]. XB distances are in Å and A–I···B angles are in degrees. Hydrogen atoms are omitted for clarity.
Molecules 25 01045 g002
Molecules 25 01045 sch002 550
Scheme 2. Fluoroiodobenzene-catalyzed hydrocyanation of imines.
Scheme 2. Fluoroiodobenzene-catalyzed hydrocyanation of imines.
Molecules 25 01045 sch002
Molecules 25 01045 g003 550
Figure 3. Schematic reaction profiles of (a) uncatalyzed hydrocyanation of imine in the gas phase (black solid line), in toluene (red dashed line), 9-catalyzed in toluene (blue dotted line), and 12-catalyzed in toluene (purple short dashed line); (b) mechanism of the uncatalyzed reaction; (c) mechanism of the XB-catalyzed reaction.
Figure 3. Schematic reaction profiles of (a) uncatalyzed hydrocyanation of imine in the gas phase (black solid line), in toluene (red dashed line), 9-catalyzed in toluene (blue dotted line), and 12-catalyzed in toluene (purple short dashed line); (b) mechanism of the uncatalyzed reaction; (c) mechanism of the XB-catalyzed reaction.
Molecules 25 01045 g003
Molecules 25 01045 g004 550
Figure 4. Calculated reaction barriers for uncatalyzed and XB-catalyzed Diels–Alder reactions.
Figure 4. Calculated reaction barriers for uncatalyzed and XB-catalyzed Diels–Alder reactions.
Molecules 25 01045 g004
Molecules 25 01045 g005 550
Figure 5. Optimized transition states, PhI-3-TS-endo and CAT-3-perFPhI-TS-endo, showing the similar halogen bond lengths. Interaction distances are shown in Å. Hydrogen atoms are omitted for clarity.
Figure 5. Optimized transition states, PhI-3-TS-endo and CAT-3-perFPhI-TS-endo, showing the similar halogen bond lengths. Interaction distances are shown in Å. Hydrogen atoms are omitted for clarity.
Molecules 25 01045 g005
Molecules 25 01045 g006 550
Figure 6. Uncatalyzed (red solid line) and I2-calculated (blue dotted line) reaction profiles for intramolecular cyclization of aminochalcone (21).
Figure 6. Uncatalyzed (red solid line) and I2-calculated (blue dotted line) reaction profiles for intramolecular cyclization of aminochalcone (21).
Molecules 25 01045 g006
Molecules 25 01045 g007 550
Figure 7. Calculated reaction profiles of uncatalyzed (black solid line), I2 (blue dotted line), and HI-catalyzed (red dashed line) intermolecular Michael addition of indole to trans-crotonophenone (25).
Figure 7. Calculated reaction profiles of uncatalyzed (black solid line), I2 (blue dotted line), and HI-catalyzed (red dashed line) intermolecular Michael addition of indole to trans-crotonophenone (25).
Molecules 25 01045 g007
Molecules 25 01045 g008 550
Figure 8. NBO population analysis of XB interaction energies for selected reactions.
Figure 8. NBO population analysis of XB interaction energies for selected reactions.
Molecules 25 01045 g008
Molecules 25 01045 g009 550
Figure 9. Calculated reaction profiles for the cyclization step of I2-catalyzed iso-Nazarov cyclization of conjugated dienals. Interaction distances are given in Å.
Figure 9. Calculated reaction profiles for the cyclization step of I2-catalyzed iso-Nazarov cyclization of conjugated dienals. Interaction distances are given in Å.
Molecules 25 01045 g009
Molecules 25 01045 g010 550
Figure 10. Calculated reaction profiles for the C–C bond addition step of the uncatalyzed and dihalogen (X2)-catalyzed Michael addition reactions, at the M06-2X/def2-TZVP level. Reaction energies are reported in kcal/mol and free energies at 298.15 K and 1 atm are given in parentheses. Overlaid transition state (TS) structures are shown at the bottom and colored as follows: uncatalyzed black, F2 cyan, Cl2 green, Br2 red, and I2 purple.
Figure 10. Calculated reaction profiles for the C–C bond addition step of the uncatalyzed and dihalogen (X2)-catalyzed Michael addition reactions, at the M06-2X/def2-TZVP level. Reaction energies are reported in kcal/mol and free energies at 298.15 K and 1 atm are given in parentheses. Overlaid transition state (TS) structures are shown at the bottom and colored as follows: uncatalyzed black, F2 cyan, Cl2 green, Br2 red, and I2 purple.
Molecules 25 01045 g010
Molecules 25 01045 g011 550
Figure 11. Calculated activation barriers for Michael addition reactions catalyzed by dihalogens versus the HOMOpy–LUMO gap Δε, at the M06-2X/def2-TZVP level.
Figure 11. Calculated activation barriers for Michael addition reactions catalyzed by dihalogens versus the HOMOpy–LUMO gap Δε, at the M06-2X/def2-TZVP level.
Molecules 25 01045 g011
Molecules 25 01045 sch003 550
Scheme 3. Zinc acetate-catalyzed iodolactonization reaction of allyl acetic acid (35).
Scheme 3. Zinc acetate-catalyzed iodolactonization reaction of allyl acetic acid (35).
Molecules 25 01045 sch003
Molecules 25 01045 sch004 550
Scheme 4. Reduction of quinoline by Hantzsch ester catalyzed by imidazolinium and imidazolium.
Scheme 4. Reduction of quinoline by Hantzsch ester catalyzed by imidazolinium and imidazolium.
Molecules 25 01045 sch004
Molecules 25 01045 g012 550
Figure 12. Calculated reaction profiles for the uncatalyzed (red solid line) and halogen bond-catalyzed (blue dotted line) pathways. Distances are in Å and A–I···B angles are in degrees. C–H hydrogen atoms except for the transferring hydride or proton are omitted for clarity.
Figure 12. Calculated reaction profiles for the uncatalyzed (red solid line) and halogen bond-catalyzed (blue dotted line) pathways. Distances are in Å and A–I···B angles are in degrees. C–H hydrogen atoms except for the transferring hydride or proton are omitted for clarity.
Molecules 25 01045 g012
Molecules 25 01045 g013 550
Figure 13. Calculated pathways for Brønsted acid-catalyzed (black solid line) and XB-catalyzed (blue dotted line) reduction of quinoline by 39. For comparison, the decomposition of 40 to generate Brønsted acid catalyst is shown in red dashed line.
Figure 13. Calculated pathways for Brønsted acid-catalyzed (black solid line) and XB-catalyzed (blue dotted line) reduction of quinoline by 39. For comparison, the decomposition of 40 to generate Brønsted acid catalyst is shown in red dashed line.
Molecules 25 01045 g013
Molecules 25 01045 g014 550
Figure 14. Calculated reaction profiles for uncatalyzed (red solid line) and iodoimidazolinium 47-catalyzed (blue dotted line) conjugate addition of methylthiophene to enone.
Figure 14. Calculated reaction profiles for uncatalyzed (red solid line) and iodoimidazolinium 47-catalyzed (blue dotted line) conjugate addition of methylthiophene to enone.
Molecules 25 01045 g014
Molecules 25 01045 g015 550
Figure 15. Calculated XB and π···π interaction complexes between 48 and 49. Interaction distances are in Å and A–I···B angles are in degrees. Hydrogen atoms are omitted for clarity.
Figure 15. Calculated XB and π···π interaction complexes between 48 and 49. Interaction distances are in Å and A–I···B angles are in degrees. Hydrogen atoms are omitted for clarity.
Molecules 25 01045 g015
Molecules 25 01045 g016 550
Figure 16. Transition states of [4+2] cycloaddition between indoles. Interaction distances are in Å and A–I···B angles are in degrees. Hydrogen atoms are omitted for clarity.
Figure 16. Transition states of [4+2] cycloaddition between indoles. Interaction distances are in Å and A–I···B angles are in degrees. Hydrogen atoms are omitted for clarity.
Molecules 25 01045 g016
Molecules 25 01045 g017 550
Figure 17. Calculated reaction profiles for the uncatalyzed and ICl3-catalyzed ring-opening polymerization of l-lactide. The uncatalyzed concerted pathway is shown as a black solid line, the uncatalyzed stepwise pathway is shown as a red dotted line, the XB-catalyzed concerted pathway is shown as a blue dashed line, and the catalyzed stepwise pathway is shown as a purple dash-dotted line.
Figure 17. Calculated reaction profiles for the uncatalyzed and ICl3-catalyzed ring-opening polymerization of l-lactide. The uncatalyzed concerted pathway is shown as a black solid line, the uncatalyzed stepwise pathway is shown as a red dotted line, the XB-catalyzed concerted pathway is shown as a blue dashed line, and the catalyzed stepwise pathway is shown as a purple dash-dotted line.
Molecules 25 01045 g017
Table
Table 1. Calculated binding energies (ΔG298 and ΔG298) and interaction distances (DXB) of the XB complex between iodopentafluorobenzene and triethylamine using various density functional theory (DFT) methods.
Table 1. Calculated binding energies (ΔG298 and ΔG298) and interaction distances (DXB) of the XB complex between iodopentafluorobenzene and triethylamine using various density functional theory (DFT) methods.
DFT aΔH298
(kcal/mol)		ΔG298 b
(kcal/mol)		DXB
(Å)
MN15−10.1−1.02.75
B3LYP−1.67.22.87
B3LYP-D3−8.11.42.79
M06-2X−8.21.22.80
ω-B97XD−6.92.42.85
PBE0−4.15.02.78
PBE0-D3−8.21.12.74
a All calculations were performed at the DFT/6-311++G(2d,p)//DFT/6-31+G(d) level. Detailed computational results are given in Supplementary Materials. Free energy corrections were calculated at 298 K and with correction to the standard state. b Experimentally determined binding free energy at 298 K in cyclohexane: ΔG298 = −0.2 ± 0.1 kcal/mol [51].
Table
Table 2. Comparison of reaction kinetics between uncatalyzed and CAT-3-perFPhI-catalyzed Claisen rearrangement reaction.
Table 2. Comparison of reaction kinetics between uncatalyzed and CAT-3-perFPhI-catalyzed Claisen rearrangement reaction.
Molecules 25 01045 i001
Uncatalyzed18-Catalyzed
T(k)ΔG≠
(kcal/mol)		kKeq
(M h−1)		ΔG≠n-hexane (kcal/mol)TOF
(h−1)
318.1526.55.3×10−428.38.6×10−4
298.1526.53.3×10−527.32.3×10−4
273.1526.45.3×10−726.02.5×10−5

Share and Cite

MDPI and ACS Style

Yang, H.; Wong, M.W. Application of Halogen Bonding to Organocatalysis: A Theoretical Perspective. Molecules 2020, 25, 1045. https://doi.org/10.3390/molecules25051045

AMA Style

Yang H, Wong MW. Application of Halogen Bonding to Organocatalysis: A Theoretical Perspective. Molecules. 2020; 25(5):1045. https://doi.org/10.3390/molecules25051045

Chicago/Turabian Style

Yang, Hui, and Ming Wah Wong. 2020. "Application of Halogen Bonding to Organocatalysis: A Theoretical Perspective" Molecules 25, no. 5: 1045. https://doi.org/10.3390/molecules25051045

APA Style

Yang, H., & Wong, M. W. (2020). Application of Halogen Bonding to Organocatalysis: A Theoretical Perspective. Molecules, 25(5), 1045. https://doi.org/10.3390/molecules25051045

Article Metrics

Back to TopTop