Anharmonic Thermal Motion Modelling in the Experimental XRD Charge Density Determination of 1-Methyluracil at T = 23 K
Abstract
:1. Introduction
2. Experimental
Multipolar Refinement of Four Models
3. Results and Discussion
3.1. Hamilton’s Test
3.2. Analysis of Charge Density Residuals
3.3. Molecular Dynamics
3.4. The Positional Parameters
3.5. The Anharmonicity Gram–Charlier Coefficients
3.6. The Nuclear Anisotropic Thermal Parameters
3.7. Atomic Charges and Volumes
3.8. Molecular Electrostatic Moments
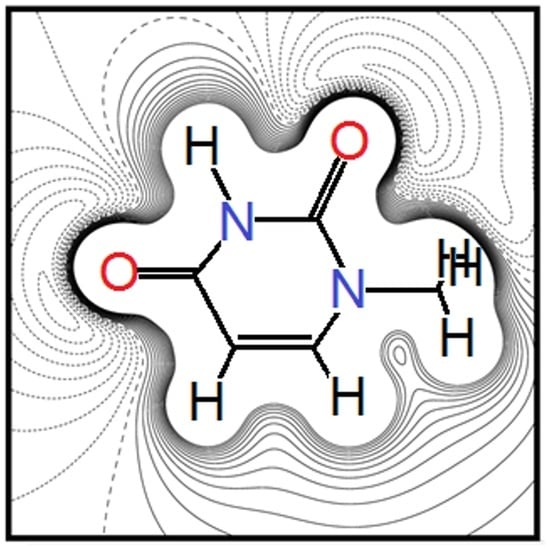
3.9. The Electrostatic Potential Φmol
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Taylor, R.; Wood, P.A. A Million Crystal Structures: The Whole Is Greater than the Sum of Its Parts. Chem. Rev. 2019, 119, 9427–9477. [Google Scholar] [CrossRef]
- Pullen, S.; Hiller, W.G.; Lippert, B. Regarding the diamagnetic components in Rosenberg’s “platinum pyrimidine blues”: Species in the cis-Pt(NH3)2-1-methyluracil system. Inorg. Chim. Acta 2019, 494, 168–180. [Google Scholar] [CrossRef]
- Ostakhov, S.S.; Ovchinnikov, M.Y.; Masyagutova, G.A.; Khursan, S.L. Luminescent and DFT Study of Keto–Enol Tautomers of 5-Fluorouracil and Its Derivatives in Aqueous Solutions. J. Phys. Chem. A 2019, 123, 7956–7964. [Google Scholar] [CrossRef] [PubMed]
- Portalone, G.; Rissanen, K. Multifacial Recognition in Binary and Ternary Cocrystals from 5-Halouracil and Aminoazine Derivatives. Cryst. Growth Des. 2018, 18, 5904–5918. [Google Scholar] [CrossRef] [Green Version]
- Brela, M.Z.; Boczar, M.; Malec, L.M.; Wójcik, M.J.; Nakajima, T. Spectroscopic study of uracil, 1-methyluracil and 1-methyl-4-thiouracil: Hydrogen bond interactions in crystals and ab-initio molecular dynamics. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 197, 194–201. [Google Scholar] [CrossRef] [PubMed]
- Huan, G.; Xu, T.; Momen, R.; Wang, L.; Ping, Y.; Kirk, S.R.; Jenkins, S.; van Mourik, T. A QTAIM exploration of the competition between hydrogen and halogen bonding in halogenated 1-methyluracil: Water systems. Chem. Phys. Lett. 2016, 662, 67–72. [Google Scholar] [CrossRef] [Green Version]
- Vogt, N.; Marochkin, I.I.; Rykov, A.N.; Dorofeeva, O.V. Interplay of Experiment and Theory: Determination of an Accurate Equilibrium Structure of 1-Methyluracil by the Gas Electron Diffraction Method and Coupled-Cluster Computations. J. Phys. Chem. A 2013, 117, 11374–11381. [Google Scholar] [CrossRef]
- Bader, R.F.M. Atoms in Molecules. A Quantum Theory; Clarendon Press: Oxford, UK, 1995; ISBN 0198558651. [Google Scholar]
- Köhler, C.; Lübben, J.; Krause, L.; Hoffmann, C.; Herbst-Irmer, R.; Stalke, D. Comparison of different strategies for modelling hydrogen atoms in charge density analyses. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2019, 75, 434–441. [Google Scholar] [CrossRef] [Green Version]
- Fugel, M.; Jayatilaka, D.; Hupf, E.; Overgaard, J.; Hathwar, V.R.; Macchi, P.; Turner, M.J.; Howard, J.A.K.K.; Dolomanov, O.V.; Puschmann, H.; et al. Probing the accuracy and precision of Hirshfeld atom refinement with HARt interfaced with Olex2. IUCrJ 2018, 5, 32–44. [Google Scholar] [CrossRef]
- Malaspina, L.A.; Hoser, A.A.; Edwards, A.J.; Woińska, M.; Turner, M.J.; Price, J.R.; Sugimoto, K.; Nishibori, E.; Bürgi, H.-B.; Jayatilaka, D.; et al. Hydrogen atoms in bridging positions from quantum crystallographic refinements: Influence of hydrogen atom displacement parameters on geometry and electron density. CrystEngComm 2020, 22, 4778–4789. [Google Scholar] [CrossRef]
- Chodkiewicz, M.L.; Woińska, M.; Woźniak, K. Hirshfeld atom like refinement with alternative electron density partitions. IUCrJ 2020, 7, 1199–1215. [Google Scholar] [CrossRef]
- Dittrich, B.; Lübben, J.; Mebs, S.; Wagner, A.; Luger, P.; Flaig, R. Accurate Bond Lengths to Hydrogen Atoms from Single-Crystal X-ray Diffraction by Including Estimated Hydrogen ADPs and Comparison to Neutron and QM/MM Benchmarks. Chem. A Eur. J. 2017, 23, 4605–4614. [Google Scholar] [CrossRef] [PubMed]
- Madsen, A.Ø.; Hoser, A.A. SHADE3 server: A streamlined approach to estimate H-atom anisotropic displacement parameters using periodic ab initio calculations or experimental information. J. Appl. Crystallogr. 2014, 47, 2100–2104. [Google Scholar] [CrossRef]
- Munshi, P.; Madsen, A.Ø.; Spackman, M.A.; Larsen, S.; Destro, R. Estimated H-atom anisotropic displacement parameters: A comparison between different methods and with neutron diffraction results. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Whitten, A.E.; Spackman, M.A. Anisotropic displacement parameters for H atoms using an ONIOM approach. Acta Crystallogr. Sect. B Struct. Sci. 2006, 62, 875–888. [Google Scholar] [CrossRef] [Green Version]
- Roversi, P.; Destro, R. Approximate anisotropic displacement parameters for H atoms in molecular crystals. Chem. Phys. Lett. 2004, 386, 472–478. [Google Scholar] [CrossRef]
- Stewart, R.F.; Spackman, M.A.; Flensburg, C. VALRAY User’s Manual (Version 2.1); Carnegie Mellon University: Pittsburg, PA, USA; University of Copenhagen: Copenhagen, Denmark, 2000. [Google Scholar]
- Restori, R.; Schwarzenbach, D. Anharmonic Motion vs Chemical Bonding: On the Interpretation of Electron Densities Determined by X-ray Diffraction. Acta Crystallogr. Sect. A Found. Crystallogr. 1996, 52, 369–378. [Google Scholar] [CrossRef]
- Destro, R.; Ruffo, R.; Roversi, P.; Soave, R.; Loconte, L.; Lo Presti, L. Anharmonic motions versus dynamic disorder at the Mg ion from the charge densities in pyrope (Mg3Al2Si3O12) crystals at 30 K: Six of one, half a dozen of the other. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2017, 73, 722–736. [Google Scholar] [CrossRef] [Green Version]
- Finocchio, G.; Rizzato, S.; Macetti, G.; Tusha, G.; Lo Presti, L. Unravelling the Chemistry of the [Cu(4,7-Dichloroquinoline)2Br2]2 Dimeric Complex through Structural Analysis: A Borderline Ligand Field Case. Crystals 2020, 10, 477. [Google Scholar] [CrossRef]
- Kuhs, W.F. The Anharmonic Temperature Factor in Crystallographic Structure Analysis. Aust. J. Phys. 1988, 41, 369–382. [Google Scholar] [CrossRef]
- Kuhs, W.F. Generalized atomic displacements in crystallographic structure analysis. Acta Crystallogr. Sect. A Found. Crystallogr. 1992, 48, 80–98. [Google Scholar] [CrossRef]
- Mallinson, P.R.; Koritsanszky, T.; Elkaim, E.; Li, N.; Coppens, P. The Gram–Charlier and multipole expansions in accurate X-ray diffraction studies: Can they be distinguished? Acta Crystallogr. Sect. A Found. Crystallogr. 1988, 44, 336–343. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, H.O.; Stewart, R.F.; McIntyre, G.J.; Larsen, S. Simultaneous variation of multipole parameters and Gram–Charlier coefficients in a charge-density study of tetrafluoroterephthalonitrile based on X-ray and neutron data. Acta Crystallogr. Sect. A Found. Crystallogr. 2003, 59, 540–550. [Google Scholar] [CrossRef]
- Lo Presti, L.; Sist, M.; Loconte, L.; Pinto, A.; Tamborini, L.; Gatti, C. Rationalizing the lacking of inversion symmetry in a noncentrosymmetric polar racemate: An experimental and theoretical study. Cryst. Growth Des. 2014, 14, 5822–5833. [Google Scholar] [CrossRef] [Green Version]
- Meindl, K.; Herbst-Irmer, R.; Henn, J. On the effect of neglecting anharmonic nuclear motion in charge density studies. Acta Crystallogr. Sect. A Found. Crystallogr. 2010, 66, 362–371. [Google Scholar] [CrossRef] [PubMed]
- Herbst-Irmer, R.; Henn, J.; Holstein, J.J.; Hübschle, C.B.; Dittrich, B.; Stern, D.; Kratzert, D.; Stalke, D. Anharmonic Motion in Experimental Charge Density Investigations. J. Phys. Chem. A 2013, 117, 633–641. [Google Scholar] [CrossRef]
- McMullan, R.K.; Craven, B.M. Crystal structure of 1-methyluracil from neutron diffraction at 15, 60 and 123 K. Acta Crystallogr. Sect. B Struct. Sci. 1989, 45, 270–276. [Google Scholar] [CrossRef]
- Klooster, W.T.; Swaminathan, S.; Nanni, R.; Craven, B.M. Electrostatic properties of 1-methyluracil from diffraction data. Acta Crystallogr. Sect. B Struct. Sci. 1992, 48, 217–227. [Google Scholar] [CrossRef]
- Hamilton, W.C. Significance tests on the crystallographic R factor. Acta Crystallogr. 1965, 18, 502–510. [Google Scholar] [CrossRef]
- Barzaghi, M. PAMoC (Version RV-2021). 2021. Available online: https://www.pamoc.it (accessed on 25 March 2021).
- Destro, R.; Loconte, L.; Lo Presti, L.; Roversi, P.; Soave, R. On the role of data quality in experimental charge-density studies. Acta Crystallogr. Sect. A Found. Crystallogr. 2004, 60, 365–370. [Google Scholar] [CrossRef] [Green Version]
- Samson, S.; Goldish, E.; Dick, C.J. A novel low-temperature X-ray goniometer with closed-cycle cooling to about 18 K. J. Appl. Crystallogr. 1980, 13, 425–432. [Google Scholar] [CrossRef]
- Destro, R.; Roversi, P.; Barzaghi, M.; Marsh, R.E. Experimental Charge Density of α-Glycine at 23 K. J. Phys. Chem. A 2000, 104, 1047–1054. [Google Scholar] [CrossRef] [Green Version]
- Roversi, P.; Merati, F.; Destro, R.; Barzaghi, M. Charge density in crystalline citrinin from X-ray diffraction at 19 K. Can. J. Chem. 1996, 74, 1145–1161. [Google Scholar] [CrossRef]
- Destro, R.; Marsh, R.E.; Bianchi, R. A low-temperature (23 K) study of L-alanine. J. Phys. Chem. 1988, 92, 966–973. [Google Scholar] [CrossRef]
- Destro, R.; Marsh, R.E. Scan-truncation corrections in single-crystal diffractometry: An empirical method. Acta Crystallogr. Sect. A Found. Crystallogr. 1987, 43, 711–718. [Google Scholar] [CrossRef]
- Destro, R. Experimental Determination of Scan-truncation Losses from Low-temperature (16 K) Single-crystal X-ray Measurements. Aust. J. Phys. 1988, 41, 503–510. [Google Scholar] [CrossRef] [Green Version]
- Destro, R.; Marsh, R.E. On predicting scan profiles: The nature of the ‘aberration function2019’. Acta Crystallogr. Sect. A Found. Crystallogr. 1993, 49, 183–190. [Google Scholar] [CrossRef] [Green Version]
- Stewart, R.F. Generalized X-ray Scattering Factors. J. Chem. Phys. 1969, 51, 4569–4577. [Google Scholar] [CrossRef]
- Stewart, R.F. Electron population analysis with rigid pseudoatoms. Acta Crystallogr. Sect. A 1976, 32, 565–574. [Google Scholar] [CrossRef]
- Jeffrey, G.A.; Piniella, J.F. (Eds.) The Application of Charge Density Research to Chemistry and Drug Design; NATO ASI Series; Nato Scien; Springer: Boston, MA, USA, 1991; Volume 250, ISBN 978-0-306-43880-6. [Google Scholar]
- Becker, P.J.; Coppens, P. Extinction within the limit of validity of the Darwin transfer equations. I. General formalism for primary and secondary extinction and their applications to spherical crystals. Acta Crystallogr. Sect. A 1974, 30, 129–147. [Google Scholar] [CrossRef]
- Spackman, M.A. Expressions for first and second derivatives in least-squares refinements including extinction. J. Appl. Crystallogr. 1987, 20, 256–258. [Google Scholar] [CrossRef]
- Meindl, K.; Henn, J. Foundations of residual-density analysis. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 404–418. [Google Scholar] [CrossRef] [PubMed]
- Soper, D.S. Critical F-Value Calculator. Available online: https://www.danielsoper.com/statcalc (accessed on 24 January 2021).
- Henn, J.; Meindl, K. More about systematic errors in charge-density studies. Acta Crystallogr. Sect. A Found. Adv. 2014, 70, 499–513. [Google Scholar] [CrossRef] [PubMed]
- Gavezzotti, A.; Lo Presti, L. Molecular dynamics simulation of organic crystals: Introducing the CLP-dyncry environment. J. Appl. Crystallogr. 2019, 52, 1253–1263. [Google Scholar] [CrossRef]
- Lo Presti, L.; Gavezzotti, A. MiCMoS—Milano Chemistry Molecular Simulation. In MiCMoS User’s Manual v1.2. 2020. Available online: https://sites.unimi.it/xtal_chem_group (accessed on 15 February 2021).
- Rizzato, S.; Gavezzotti, A.; Lo Presti, L. Molecular Dynamics Simulation of Molecular Crystals under Anisotropic Compression: Bulk and Directional Effects in Anthracene and Paracetamol. Cryst. Growth Des. 2020, 20, 7421–7428. [Google Scholar] [CrossRef]
- Gavezzotti, A.; Lo Presti, L.; Rizzato, S. Mining the Cambridge Database for theoretical chemistry. Mi-LJC: A new set of Lennard-Jones–Coulomb atom–atom potentials for the computer simulation of organic condensed matter. CrystEngComm 2020, 22, 7350–7360. [Google Scholar] [CrossRef]
- Colombo, V.; Lo Presti, L.; Gavezzotti, A. Two-component organic crystals without hydrogen bonding: Structure and intermolecular interactions in bimolecular stacking. CrystEngComm 2017, 19, 2413–2423. [Google Scholar] [CrossRef] [Green Version]
- Macetti, G.; Loconte, L.; Rizzato, S.; Gatti, C.; Lo Presti, L. Intermolecular Recognition of the Antimalarial Drug Chloroquine: A Quantum Theory of Atoms in Molecules-Density Functional Theory Investigation of the Hydrated Dihydrogen Phosphate Salt from the 103 K X-ray Structure. Cryst. Growth Des. 2016, 16, 6043–6054. [Google Scholar] [CrossRef] [Green Version]
- Thornley, F.R.; Kennedy, N.S.J.; Nelmes, R.J. Structural studies of boracites. IV. Thermal motion in cubic Ni 3 B 7 O 13 I at 77 K. J. Phys. C Solid State Phys. 1976, 9, 681–692. [Google Scholar] [CrossRef]
- Destro, R.; Roversi, P.; Soave, R.; Hovestad, A.; Lo Presti, L. Experimental Charge Density Analysis and Electrostatic Properties of Crystalline 1,3-Bis(Dimethylamino)Squaraine and Its Dihydrate from Low Temperature (T = 18 and 20 K) XRD Data. Crystals 2020, 10, 894. [Google Scholar] [CrossRef]
- Destro, R.; Soave, R.; Barzaghi, M.; Lo Presti, L. Progress in the understanding of drug-receptor interactions, Part 1: Experimental charge-density study of an angiotensin II receptor antagonist (C30H30N6O3S) at T = 17 K. Chem. A Eur. J. 2005, 11, 4621–4634. [Google Scholar] [CrossRef] [PubMed]
- Destro, R.; Soave, R.; Barzaghi, M. Physicochemical properties of zwitterionic L- and DL-alanine crystals from their experimental and theoretical charge densities. J. Phys. Chem. B 2008, 112, 5163–5174. [Google Scholar] [CrossRef] [PubMed]
- Flensburg, C.; Madsen, D. Atoms in crystals–from experimental charge densities. Acta Crystallogr. Sect. A Found. Crystallogr. 2000, 56, 24–28. [Google Scholar] [CrossRef] [Green Version]
- Flensburg, C.; Larsen, S.; Stewart, R.F. Experimental charge density study of methylammonium hydrogen succinate monohydrate. A salt with a very short O-H-O hydrogen bond. J. Phys. Chem. 1995, 99, 10130–10141. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Spackman, M.A. Molecular electric moments from X-ray diffraction data. Chem. Rev. 1992, 92, 1769–1797. [Google Scholar] [CrossRef]
- Kulakowska, I.; Geller, M.; Lesyng, B.; Wierzchowski, K.L. Dipole moments of 2,4-diketopyrimidines: Part II: Uracil, thymine and their derivatives. Biochim. Biophys. Acta Nucleic Acids Protein Synth. 1974, 361, 119–130. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian16 (Revision, A.03); Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Soave, R.; Barzaghi, M.; Destro, R. Progress in the Understanding of Drug–Receptor Interactions, Part 2: Experimental and Theoretical Electrostatic Moments and Interaction Energies of an Angiotensin II Receptor Antagonist (C30H30N6O3S). Chem. A Eur. J. 2007, 13, 6942–6956. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Appendix 2. A Deformation Density Refinement Program. Isr. J. Chem. 1977, 16, 226–229. [Google Scholar] [CrossRef]
- Lo Presti, L.; Orlando, A.M.; Loconte, L.; Destro, R.; Ortoleva, E.; Soave, R.; Gatti, C. Single N-C bond becomes shorter than a formally double N=C bond in a thiazete-1,1-dioxide crystal: An experimental and theoretical study of strong crystal field effects. Cryst. Growth Des. 2014, 14, 4418–4429. [Google Scholar] [CrossRef]
- Gionda, A.; Macetti, G.; Loconte, L.; Rizzato, S.; Orlando, A.M.; Gatti, C.; Lo Presti, L. A variable-temperature X-ray diffraction and theoretical study of conformational polymorphism in a complex organic molecule (DTC). RSC Adv. 2018, 8, 38445–38454. [Google Scholar] [CrossRef] [Green Version]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL 14: User’s Manual; University of Torino: Torino, Italy, 2014; pp. 1–382. [Google Scholar]
- Peintinger, M.F.; Oliveira, D.V.; Bredow, T. Consistent Gaussian basis sets of triple-zeta valence with polarization quality for solid-state calculations. J. Comput. Chem. 2013, 34, 451–459. [Google Scholar] [CrossRef]
- Lo Presti, L. On the significance of weak hydrogen bonds in crystal packing: A large databank comparison of polymorphic structures. CrystEngComm 2018, 20, 5976–5989. [Google Scholar] [CrossRef] [Green Version]
- Gavezzotti, A.; Lo Presti, L. Building Blocks of Crystal Engineering: A Large-Database Study of the Intermolecular Approach between C–H Donor Groups and O, N, Cl, or F Acceptors in Organic Crystals. Cryst. Growth Des. 2016, 16, 2952–2962. [Google Scholar] [CrossRef]
- Welberry, T.R.; Weber, T. One hundred years of diffuse scattering. Crystallogr. Rev. 2016, 22, 2–78. [Google Scholar] [CrossRef]







| Sample Information | |
|---|---|
| Empirical formula | C5H6N2O2 |
| Formula wt/g mol−1 | 126.12 |
| Crystal system | Orthorhombic |
| Space group | Ibam |
| Z | 8 |
| Crystal dimensions/mm | 0.20 × 0.28 × 0.34 |
| T/K | 23 (1) |
| a/Å | 13.208 (1) |
| b/Å | 13.164 (1) |
| c/Å | 6.1620 (6) |
| V/Å3 | 1071.4 (2) |
| Dx/g cm−3 | 1.564 |
| F (000) | 528 |
| Absorption coeff., µ/mm−1 | 0.124 |
| Data Collection | |
| Cryostat | He/closed-cycle |
| Diffractometer | Four-circle |
| λ/Å | 0.71073 |
| Monochromator | Graphite |
| (sinθ/λ)max (Å−1) | 1.143 |
| Scan technique | ω/2θ |
| Scan rate (2θ)/°min−1 | 3 |
| Scan range (2θ)/° | 2.5 + Sα1–α2 † |
| No. collected refln.s | 11,985 |
| no. unique refln.s | 3568 |
| No. obsd refln.s (I > 0, Nobs) | 3344 |
| No. refln.s with I > 3σ (I), N1 | 2614 |
| Model a | A C,N,O: lmax = 3 H: lmax = 2 | B C,N,O: lmax = 4 H: lmax = 2 | C Model B + Cijk (All Atoms) | D Model C + Dijkl (C, N, O) |
|---|---|---|---|---|
| Scale factor | 1.00027 (273) | 1.00017 (275) | 0.99982 (293) | 0.99975 (359) |
| Extinc. coeff. g11 | 0.527 (9) | 0.533 (9) | 0.531 (9) | 0.529 (9) |
| No. variables | 179 | 224 | 312 | 393 |
| On all 3344 observed (I > 0) data | ||||
| ΣwΔ2 | 3062.70858 | 2920.61101 | 2780.51474 | 2645.12507 |
| G.o.f. | 0.9837 | 0.9675 | 0.9576 | 0.9468 |
| R (F) | 0.0289 | 0.0285 | 0.0282 | 0.0277 |
| R (F2) | 0.0205 | 0.0195 | 0.0191 | 0.0185 |
| wR (F2) | 0.0337 | 0.0329 | 0.0321 | 0.0314 |
| On 115 data with (sinθ/λ) ≤ 0.35 (low-angle data) | ||||
| R (F) | 0.0053 | 0.0049 | 0.0047 | 0.0043 |
| R (F2) | 0.0120 | 0.0104 | 0.0104 | 0.0100 |
| wR (F2) | 0.0118 | 0.0110 | 0.0104 | 0.0100 |
| On 663 data with (sinθ/λ) ≤ 0.65 (i.e., within the Cu sphere) | ||||
| R (F) | 0.0111 | 0.0103 | 0.0098 | 0.0096 |
| R (F2) | 0.0123 | 0.0110 | 0.0106 | 0.0103 |
| wR (F2) | 0.0189 | 0.0171 | 0.0164 | 0.0159 |
| On 2681 data with 0.65 < (sinθ/λ) ≤ 1.15 (high-angle data) | ||||
| R (F) | 0.0389 | 0.0387 | 0.0385 | 0.0379 |
| R (F2) | 0.0339 | 0.0335 | 0.0330 | 0.0321 |
| wR (F2) | 0.0469 | 0.0465 | 0.0456 | 0.0445 |
| On 2614 data with I > 3σ (I) | ||||
| R (F) | 0.0181 | 0.0177 | 0.0173 | 0.0169 |
| R (F2) | 0.0188 | 0.0179 | 0.0174 | 0.0168 |
| wR (F2) | 0.0309 | 00301 | 0.0293 | 0.0285 |
| ΣwΔ2 | 2570.44048 | 2432.65591 | 2302.79838 | 2187.30982 |
| Δρ min | −0.23 | −0.22 | −0.21 | −0.19 |
| at X,Y (e/Å3) | 0.448; 0.067 | 0.448; 0.067 | 0.448; 0.064 | 0.329; 0.310 |
| Δρ max | +0.53 | +0.49 | +0.44 | +0.37 |
| at X,Y (e/Å3) | 0.441; 0.097 | 0.441; 0.097 | 0.443; 0.095 | 0.440; 0.095 |
| Compared Models | A vs. B | B vs. C | C vs. D | |
|---|---|---|---|---|
| b = dimension of the hypothesis | 224 − 179 = 45 | 312 − 224 = 88 | 393 − 312 = 81 | |
| n-m = degrees of freedom | 3344 − 224 = 3120 | 3344 − 312 = 3032 | 3344 − 393 = 2951 | |
| Actual R-factor ratio | √ (3062.709/2920.611) = 1.0240 | √ (2920.611/2780.515) = 1.0249 | √ (2780.515/2645.125) = 1.0253 | |
| Significance b,n-m,α | α = 0.001 | 1.0128 | 1.0222 | 1.0213 |
| α = 0.0005 | 1.0133 | 1.0227 | 1.0219 | |
| Model | A | B | C | D | Arithmetic Averages | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Atom | q | V | q | V | q | V | q | V | q | V |
| C1 | −0.040 | 12.03 | −0.022 | 11.88 | −0.012 | 11.58 | −0.018 | 11.54 | −0.02 (1) | 11.8 (2) |
| C2 | 1.369 | 4.96 | 1.393 | 4.89 | 1.437 | 4.87 | 1.390 | 4.90 | 1.40 (3) | 4.90 (3) |
| C4 | 1.125 | 6.42 | 1.173 | 6.38 | 1.212 | 6.36 | 1.232 | 6.31 | 1.19 (4) | 6.37 (4) |
| C5 | −0.027 | 12.40 | −0.047 | 12.60 | −0.022 | 12.13 | −0.059 | 12.66 | −0.04 (2) | 12.5 (2) |
| C6 | 0.148 | 9.69 | 0.145 | 9.64 | 0.146 | 9.70 | 0.174 | 9.63 | 0.15 (1) | 9.66 (3) |
| N1 | −0.962 | 10.98 | −0.952 | 10.84 | −0.978 | 10.88 | −1.003 | 10.98 | −0.97 (2) | 10.92 (6) |
| N3 | −1.036 | 13.69 | −1.022 | 13.36 | −1.021 | 13.29 | −1.058 | 13.41 | −1.03 (2) | 13.4 (2) |
| O2 | −0.948 | 16.73 | −0.982 | 16.88 | −1.033 | 16.98 | −0.975 | 16.89 | −0.99 (3) | 16.87 (9) |
| O4 | −1.005 | 16.73 | −1.053 | 17.07 | −1.071 | 17.06 | −1.045 | 16.96 | −1.04 (2) | 17.0 (1) |
| H3 | 0.565 | 1.88 | 0.563 | 1.88 | 0.537 | 2.00 | 0.546 | 2.01 | 0.55 (1) | 1.94 (6) |
| H5 | 0.136 | 6.19 | 0.128 | 6.23 | 0.129 | 6.19 | 0.140 | 6.25 | 0.133 (5) | 6.22 (3) |
| H6 | 0.180 | 5.04 | 0.183 | 5.00 | 0.183 | 4.95 | 0.196 | 4.90 | 0.185 (6) | 4.97 (5) |
| H11 | 0.164 | 4.95 | 0.169 | 5.01 | 0.175 | 4.87 | 0.173 | 4.90 | 0.170 (4) | 4.93 (5) |
| H12 | 0.165 | 6.26 | 0.161 | 6.30 | 0.160 | 6.34 | 0.154 | 6.43 | 0.160 (4) | 6.33 (6) |
| H12 | 0.165 | 6.26 | 0.161 | 6.30 | 0.160 | 6.34 | 0.154 | 6.43 | 0.160 (4) | 6.33 (6) |
| ∑ | 0 | 134.21 | 0 | 134.26 | 0 | 133.53 | 0 | 134.16 | 0 | 134.0 (3) |
| Model | ||||||
|---|---|---|---|---|---|---|
| <O (r)> # | A | B | C | D | Weighted Mean ‡ | Mulliken DMA § |
| <q> | 0 | 0 | 0 | 0 | 0 | 0.00 |
| <x> | 3.5 (3) | 3.7 (3) | 3.8 (4) | 3.6 (4) | 3.7 (2) | 3.35 |
| <y> | 4.5 (2) | 4.7 (2) | 4.4 (2) | 4.4 (2) | 4.5 (1) | 3.58 |
| |µ| * | 5.7 (3) | 6.0 (3) | 5.9 (4) | 5.7 (4) | 5.8 (2) | 4.90 |
| <xx> | −9.8 (8) | −9.9 (8) | −9 (1) | −10 (1) | −9.6 (4) | −11.27 |
| <xy> | 12.3 (7) | 12.8 (7) | 12.5 (8) | 12.5 (9) | 12.5 (4) | 9.46 |
| <yy> | 13.9 (7) | 13.9 (8) | 13.3 (9) | 13.4 (9) | 13.7 (4) | 8.60 |
| <zz> | −4.2 (5) | −4.0 (5) | −4.6 (6) | −3.8 (6) | −4.1 (3) | 2.67 |
| α | 6.4 (1) | 6.4 (1) | 6.3 (1) | 6.4 (1) | 6.38 (6) | 4.91 |
| <xxx> | 70 (3) | 70 (3) | 64 (3) | 61 (4) | 67 (2) | 69.46 |
| <yyy> | −5 (2) | −5 (2) | −5 (2) | −5 (2) | −5 (1) | −10.03 |
| <xyy> | −50 (2) | −51 (2) | −46 (2) | −44 (2) | −48 (1) | −51.30 |
| <xxy> | 33 (2) | 34 (2) | 33 (2) | 33 (2) | 33 (1) | 32.84 |
| <xzz> | −20 (2) | −20 (2) | −18 (2) | −17 (2) | −18.8 (9) | −16.80 |
| <yzz> | −28 (1) | −29 (1) | −28 (1) | −28 (1) | −28.5 (6) | −22.81 |
| <xxxx> | −112 (8) | −126 (8) | −115 (9) | −126 (10) | −119 (4) | −102.94 |
| <yyyy> | 31 (6) | 22 (6) | 23 (7) | 18 (7) | 24 (3) | 18.58 |
| <zzzz> | 11 (6) | 6 (6) | 12 (7) | 8 (7) | 9 (3) | −18.70 |
| <xxxy> | −40 (7) | −41 (7) | −31 (8) | −30 (8) | −36 (4) | −51.71 |
| <yyyx> | 72 (6) | 75 (6) | 65 (7) | 64 (7) | 70 (3) | 74.62 |
| <xxyy> | 45 (7) | 55 (7) | 52 (8) | 58 (8) | 52 (4) | 32.83 |
| <xxzz> | 66 (5) | 71 (6) | 63 (6) | 68 (6) | 67 (3) | 70.11 |
| <yyzz> | −77 (4) | −77 (4) | −76 (4) | −76 (4) | −77 (2) | −51.41 |
| <zzxy> | −33 (3) | −34 (3) | −34 (4) | −34 (4) | −33 (2) | −22.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Destro, R.; Roversi, P.; Barzaghi, M.; Lo Presti, L. Anharmonic Thermal Motion Modelling in the Experimental XRD Charge Density Determination of 1-Methyluracil at T = 23 K. Molecules 2021, 26, 3075. https://doi.org/10.3390/molecules26113075
Destro R, Roversi P, Barzaghi M, Lo Presti L. Anharmonic Thermal Motion Modelling in the Experimental XRD Charge Density Determination of 1-Methyluracil at T = 23 K. Molecules. 2021; 26(11):3075. https://doi.org/10.3390/molecules26113075
Chicago/Turabian StyleDestro, Riccardo, Pietro Roversi, Mario Barzaghi, and Leonardo Lo Presti. 2021. "Anharmonic Thermal Motion Modelling in the Experimental XRD Charge Density Determination of 1-Methyluracil at T = 23 K" Molecules 26, no. 11: 3075. https://doi.org/10.3390/molecules26113075
APA StyleDestro, R., Roversi, P., Barzaghi, M., & Lo Presti, L. (2021). Anharmonic Thermal Motion Modelling in the Experimental XRD Charge Density Determination of 1-Methyluracil at T = 23 K. Molecules, 26(11), 3075. https://doi.org/10.3390/molecules26113075