Next Article in Journal
Decaffeination and Neuraminidase Inhibitory Activity of Arabica Green Coffee (Coffea arabica) Beans: Chlorogenic Acid as a Potential Bioactive Compound
Next Article in Special Issue
From Electronegativity towards Reactivity—Searching for a Measure of Atomic Reactivity
Previous Article in Journal
Antioxidant Fusion Protein SOD1-Tat Increases the Engraftment Efficiency of Total Bone Marrow Cells in Irradiated Mice
Previous Article in Special Issue
The Topological Analysis of the ELFx Localization Function: Quantitative Prediction of Hydrogen Bonds in the Guanine–Cytosine Pair
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 26
Issue 11
10.3390/molecules26113401
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Large Stabilization Effects by Intramolecular Beryllium Bonds in Ortho-Benzene Derivatives

by
Tsai I-Ting
1,
M. Merced Montero-Campillo
1,*,
Ibon Alkorta
2,*,
José Elguero
2 and
Manuel Yáñez
1,*
1
Departamento de Química, Módulo 13, Facultad de Ciencias, and Institute of Advanced Chemical Sciences (IAdChem), Universidad Autónoma de Madrid, Campus de Excelencia UAM-CSIC, Cantoblanco, 28049 Madrid, Spain
2
Instituto de Química Médica, IQM-CSIC, Juan de la Cierva, 3, 28006 Madrid, Spain
*
Authors to whom correspondence should be addressed.
Molecules 2021, 26(11), 3401; https://doi.org/10.3390/molecules26113401
Submission received: 13 May 2021 / Revised: 31 May 2021 / Accepted: 1 June 2021 / Published: 4 June 2021
(This article belongs to the Special Issue Chemical Bonding: A Commemorative Special Issue Honoring Professor Linus Pauling)
Browse Figures
Versions Notes

Abstract

:
Intramolecular interactions are shown to be key for favoring a given structure in systems with a variety of conformers. In ortho-substituted benzene derivatives including a beryllium moiety, beryllium bonds provide very large stabilizations with respect to non-bound conformers and enthalpy differences above one hundred kJ·mol−1 are found in the most favorable cases, especially if the newly formed rings are five or six-membered heterocycles. These values are in general significantly larger than hydrogen bonds in 1,2-dihidroxybenzene. Conformers stabilized by a beryllium bond exhibit the typical features of this non-covalent interaction, such as the presence of a bond critical point according to the topology of the electron density, positive Laplacian values, significant geometrical distortions and strong interaction energies between the donor and acceptor quantified by using the Natural Bond Orbital approach. An isodesmic reaction scheme is used as a tool to measure the strength of the beryllium bond in these systems in terms of isodesmic energies (analogous to binding energies), interaction energies and deformation energies. This approach shows that a huge amount of energy is spent on deforming the donor–acceptor pairs to form the new rings.

Graphical Abstract

1. Introduction

Non-covalent interactions (NCI), first introduced by J. D. van der Waals in the late 19th century [1], occupy a well-deserved relevant place in modern chemistry, biochemistry and material science and they are responsible, for instance, for the self-assembly in supramolecular structures in living beings, the efficiency of new materials for hydrogen storage or simply the properties of water and possess important implications for life on Earth [2,3,4,5]. However, a great variety of interactions covering a considerable range of energies (from a few to more than 100 kJ·mol−1) are included under the NCI label. They present some common features but are in fact associated to many different elements from the periodic table acting as Lewis acceptors towards Lewis donors. The characterization of NCI has certainly enriched the concept of chemical bonding initially associated, in a seminal work by Linus Pauling [6], to electron sharing, which is an idea that will be expanded by including, in addition to conventional covalent or ionic bonds, new weak interactions such as the hydrogen bonds [7,8]. Nowadays, there is a long list of NCIs according to the acceptor nature [9]: the aforementioned hydrogen bonds (H) [10], dihydrogen bonds (H) [11,12], alkaline-earth bonds (atoms of column 2 of the periodic table) [13,14], triel bonds (column 13) [15,16], tetrel bonds (column 14) [17], pnictogen bonds (N, P, As) [18,19], chalcogen bonds (O, S, Se, Te) [20] or halogen bonds (F, Cl, Br, I) [21,22].
Beryllium bonds, which are a type of alkaline-earth bond, are stabilized by electrostatic forces in combination with a certain amount of charge transfer [13] such as common hydrogen bonds. The electron-deficient nature of beryllium leads to strong interactions with typical Lewis bases holding lone pairs such as nitrogen or oxygen-containing bases, but also unexpectedly with boron acting as a Lewis base and it demonstrates the versatility and excellent capabilities of beryllium as a Lewis acid [23]. When a donor forms a beryllium bond with a given BeX2 moiety, the p empty Be orbital and the σ* antibonding Be-X orbital are involved in the closed-shell interaction accepting charge, with some consequences on the BeX2 geometry such as the elongation of the Be-X bonds and the bending of the X-Be-X linear arrangement. Deformation is, therefore, a clear signature of the strength of this kind of bond [24]. The charge redistribution upon beryllium bond formation provokes great changes on the intrinsic physicochemical properties of the system acting as a Lewis base to the point that strong acids can behave as bases and vice versa [25,26].
Taking into account the ability of a beryllium bond to dramatically change the nature of the donor system, it is reasonable to think of beryllium bonds as powerful modulators of the intramolecular stability of a system containing a potential Lewis pair involving beryllium [27]. Intramolecular magnesium bonds, a related alkaline-earth NCI, have been shown to play an important role on malonaldehyde-like systems [28]. Similarly, intramolecular hydrogen bonds (IMHBs) are considered responsible for the stability of the most stable conformer in 1,2-dihidroxybenzene (catechol) based on several experimental [29,30,31,32] and theoretical studies [33,34,35], although the real existence of such IMHB has been questioned by some authors [36]. What is true is that ortho-substituted benzene derivatives, thanks to its structural simplicity and a certain rigidity, can be an excellent model for testing the stability given by a non-covalent intramolecular interaction between the substituents at positions 1 and 2 and that allows a systematic modification of the ortho substituents without further modifications of the hosting molecular framework.
Following this idea, in this work we intend to evaluate the importance that a beryllium bond may have on ortho-substituted benzenes (see Scheme 1) in which a set of substituents containing beryllium (-BeH, -BeF, and -BeCl, within carbon chains of different length), acting as Lewis acids, is attached to position 1 and a set of substituents containing donors of different types (Y = OH, NH2, SH, PH2, COOH, and CONH2), acting as Lewis bases, is attached to position 2. Our goal is to analyze the effects that the intramolecular beryllium bonds formed between the basic sites of the Y substituent and the Be atom (dotted line in Scheme 1) will have on the stabilization of the corresponding ortho-substituted benzene and the origin of these effects. It should be noted that for substituents COOH and CONH2 and the two different binding sites O or N are available to form the beryllium bond. The compounds have been selected based on their potential scientific interest although they are not known experimentally.

2. Computational Details

All the structures were fully optimized at the M06-2X/6-31+G(d,p) level of theory, with a posterior refinement of the energies with a larger 6-311+G(d,p) basis set. This density functional is well suited for the description of non-covalent interactions [37] and the chosen basis set is a good compromise between computational cost and accuracy given the size of the largest systems considered in this work. An ultrafine grid was used for all these DFT calculations. The Gaussian16 program [38] was used to obtain the different stationary points, which were characterized as the minima of the potential energy surface by computing the harmonic vibrational frequencies. Enthalpies are obtained by adding the M06-2X/6-31+G(d,p) thermal enthalpy correction to the electronic energy at the M06-2X/6-311+G(d,p) level.
The topology of the electron density was studied using the AIMAll program [39] within the Quantum Theory of Atoms in Molecules (QTAIM) framework [40]. This analysis identifies the points of topological interest of chemical relevance of different kinds: bond critical points (BCPs), ring critical points (RCP), cage critical points (CCP) and nuclear attractors (NA). Among these points, we are particularly interested in the ρ values at the BCPs as they are good indicators of the strength of a given bond embedded in different chemical frameworks. The Laplacian of the electron density (∇2ρ) and the total energy density (H) are a reflection of the nature of the bond. For a beryllium bond, we would expect positive Laplacian densities and energy densities around zero or slightly below zero. We have also used the NCI (Non-Covalent interaction) index [41] to characterize the intramolecular interactions observed in one of the structures. This method is based on the reduced density gradient and allows us to visualize, in the real space, strongly attractive, strongly repulsive and weakly attractive or repulsive non-covalent interactions. For an easier interpretation, we only used the 3D-plots with a simple color code in this work where blue, red and green stand for strongly attractive, strongly repulsive and van der Waals-range interactions, respectively. The natural bond orbital (NBO) analysis [42], which is based on the generation of localized hybrid orbitals corresponding to Lewis-type representations of the molecular structures, permits the calculation of second-order orbital interaction to quantitatively characterize donations and backdonations among occupied and empty localized molecular orbitals involved in intermolecular and/or intramolecular interactions.
Common methods to estimate the strength of intramolecular bonding are changes in geometrical parameters and topological descriptors. The estimation of the energy involved in the intramolecular interaction is also useful but admits more than one definition. The relative stability between conformers, depending on the presence or absence of the interaction, is one of the definitions. The electronic energy associated to an isodesmic reaction is another tool for calculating intramolecular interaction energies [43,44,45,46,47] and, in particular, intramolecular hydrogen bonds [48,49,50,51,52,53]. An intramolecular interaction may be formally built up by a fictitious chemical reaction and the energy of this reaction is representative of the interaction energy. The energies for the isodesmic reactions were computed according to the energy difference between products and reactants shown in Scheme 2.
Once the isodesmic energies (Eiso) are obtained, we can further refine our analysis by decomposing this energy into two terms, the deformation energy (Edef) and the interaction energy (Eint) such that Eiso = Eint + Edef, in a similar manner as was proposed in the previous literature to analyze reaction rates [54]. The interaction energy is the result of subtracting the energy of the reactants from the energy of the product in Scheme 2 but with the geometry they present in the product. Hence, the distorted geometry of the first reactant is obtained by replacing the Y substituent of the product by a H atom. For the second reactant, it is the BeX substituent (the one replaced by H) and for the third reactant both substituents are replaced by H. The deformation energy is just the difference between the energy of the isodesmic reaction and the aforementioned defined interaction energy.

3. Results and Discussion

In this section, we firstly discuss the energy differences between conformers to estimate the stabilization caused by the formation of beryllium bonds and the trends observed according to the substitution patterns. The observed trends are then rationalized in a second step by means of the NBO decomposition scheme and the topological analysis of the beryllium bond. Finally, the isodesmic energies and the decomposition of these energies into deformation and interaction energies will help to fully understand the stabilization provided by the different substituents.

3.1. Stabilization Gained by Beryllium Bond Formation

A total of 108 conformers were obtained at the M06-2X/6-311+G(d,p)//M06-2X/6-31+G(d,p) level (see Table S1 in the Supporting Information for more details). The structures will be labelled, if it is required, by simply writing the interacting pair Y:(CH2)nBeX (donor–acceptor; example: NH2:BeCl).
The stabilization energy gained by the formation of the intramolecular beryllium bond for donors Y = (OH, SH, NH2, PH2) is reported in Table 1 as the enthalpy difference ΔH1 between the conformer exhibiting a beryllium bond and the most stable one in which this interaction is not present (see Figure 1a for the particular case NH2:BeCl). For donors Y = (COOH, CONH2), there are two conformers stabilized by a beryllium bond depending on the binding site (O from carbonyl group or the OH/NH2 groups) and the stability difference between them is reported in Table 1 as enthalpy ΔH2 (see Figure 1b for the particular case COOH:CH2BeCl).
From the ΔH1 values in Table 1 it can be seen that the stabilization provided by the beryllium bond goes from 2.2 kJ·mol−1 (OH:BeH) to 87.0 kJ·mol−1 (NH2:C2H4BeCl), where in all cases the global minimum corresponds to the conformer stabilized by an intramolecular beryllium bond. Furthermore, for the set of compounds in which Y = COOH and CONH2, the global minimum and the second most stable conformer correspond to conformers stabilized by intramolecular beryllium bonds. Any other non-bound conformers for these donors, where found, is situated much higher in terms of energy (see Table S2). Our results show that in all cases the most stable of the two conformers is that in which the carbonyl oxygen is involved.
It is also important to note, as illustrated in Figure 2, that the appearance of the beryllium bond between the basic site of the Y substituent and the Be atom implies the formation of new four-membered, five-membered, six-membered or seven-membered heterocycles, depending in the length of the –(CH2)n (n = 0, 1, 2) carbon chain to which the BeX is attached.
This is a crucial feature because if we look in detail at the values in Table 1 for the donors OH, SH, NH2 and PH2, it is clear that the length of the carbon chain from zero to two carbon atoms in the acceptor (BeX, CH2BeX, and C2H4BeX) has a huge effect on the stabilization energies since this chain determines the size of the new heterocyclic ring formed on the BeB conformer. Four membered-rings (acceptor BeX), where formed, provide small stabilization with respect to the non-bound conformer, while five-membered (CH2BeX) and six-membered (C2H4BeX) rings are largely stabilized in comparison with the open form. This is, at the moment, something already expected. However, it is interesting to note that when looking at the effect of X on the beryllium unit, the stabilization gained by replacing H by F is pretty similar in many cases or even lower for F. One would expect that a more electronegative atom would make Be a better acceptor in almost all situations. Results with a BeCl moiety are pretty similar to the BeF ones in the case of four-membered rings but stabilization energies are significantly larger for five-membered and six-membered rings. The highest reported value is 87.0 kJ·mol−1 for the NH2:C2H4BeCl pair. The effect of the halogen would later be clarified in the posterior sections.
It is also worth noting that, as in all Lewis pair interactions, the quality of the electron donor plays a crucial role. It is easy to appreciate that interactions of CH2BeX and C2H4BeX acceptors with first-row donors such as OH and NH2 give place to larger stabilizations than when compared to second-row donors SH and PH2, where the stabilization decreases in the order NH2 > OH > SH > PH2. The size effect O/S and N/P is something already observed in regular intermolecular beryllium bonds [13].
The geometrical parameters in Table 2 point in the same direction and indicates strong stabilizations by the formation of the beryllium bonds. Indeed, the C-Be-X angle, which in the absence of interaction is strictly linear, becomes significantly distorted, especially for X = Cl as a sign of the strength of the interactions. It is clear, for instance, that the newly formed four-membered rings present high deviations of this angle from 180° for OH and NH2 strong donors, while much modest deviations are found for SH or PH2. Interestingly, when the length of the carbon chain increases favoring the formation of five-membered and six-membered rings, the C-Be-X angles are closer to 120° than to 180° in all cases, indicating that we can properly speak of tri-coordinated beryllium atoms.
The BeX acceptor series (the formation of a four-member ring) deserves some additional discussion. Only NH2, which is the best donor in general terms, displays significant stabilizations for the formation of a four-member ring through a beryllium bond. Very large donor-Be distances and very small deformations of the C-Be-X angle (see Table 2) are found along with the relatively low stabilization energies of the BeX series. Interestingly, for the pairs interacting at long distances, a soft atom, such as S, gives rise to slightly larger stabilizations than O, regardless of whether we take BeH (2.2 vs. 12.5 kJ·mol−1), BeF (6.7 vs. 11.3 kJ·mol−1) or BeCl (7.1 vs. 11.7 kJ·mol−1). In other words, for four-member rings, the rigidity of the benzene framework does not allow the substituents to reach significant interactions and only an extremely good donor such as N in NH2 gives rise to considerable stabilizations (NH2:BeCl, 31.3 kJ·mol−1, the case illustrated in Figure 1a). This is also consistent with the fact that for these compounds no BCP associated with the Be-Y interaction is found (see electron densities at BCP in Table S3). Furthermore, coherently, for this set the second-order NBO interaction energies are about one order of magnitude smaller than those found for the remaining derivatives (see Table S4 of the Supporting Information). Hence, we conclude that the SH and PH2 values seem to be a reflection of the dispersion forces involved more than a reflection of the beryllium bonds themselves. In other words, the absence of a BCP between the Be atoms and the basic site in these compounds does not mean that no interaction is taking place between the donor and acceptor. For regions of the 3D-space in which the electron density is deformed by weak non-covalent interactions, but not enough to give rise to a BCP, the NCI plots (see Computational Details) are very useful. Figure 3 illustrates the particular case of the PH2:BeCl structure in which a green isosurface denotes an interaction within the van der Waals range between P and Be, as is suggested when looking at the stabilization energies found for these compounds (1.4 kJ·mol−1, Table 1). However, the reason is still not obvious as to why -OH results are similar (or even smaller) than the results for -SH or -PH2 in the four-membered ring cases. We will later observe that the energy analysis might provide some answers in this respect.
The last two rows of Table 1, as mentioned above, permitted the conclusion that for Y = COOH and CONH2, the intramolecular beryllium bond involving the carbonyl group is systematically more stabilizing than the one involving the hydroxyl or the amino group, up to a maximum of 30.6 kJ·mol−1 and 57.6 kJ·mol−1, respectively. This is coherent with the relative basicity of the lone pairs in the COOH and CONH2 groups; although, in general, the isolated N is a better donor than O and resonance with the carbonyl group makes NH2 more available to donate its pair towards carbonyl than OH. These basicity differences are very well reflected in the corresponding molecular graphs. In Figure 4 we show, as a suitable example, a comparison between CO*OH:BeCl, COO*H:BeCl, CO*NH2:BeCl and CON*H2:BeCl. It can be observed that when the interaction takes place with the carbonyl group, the electron density at the BCP is larger for CONH2 (0.072 au) than for COOH (0.064 au). The role of the carbonyl group as good donors for the formation of hydrogen bonds is very well known since the 1970s and 1980s for acids, esters and amides [55,56,57,58,59]. Moreover, when the interactions involve the hydroxyl (0.058 au) or the amino group (0.065 au), they are weaker than those involving the carbonyl group but the interaction involving the amino is stronger than the interaction involving the hydroxyl group.
This picture is also consistent with the values obtained for the NBO second-order perturbation energies (see Table S4 of the Supporting Information), where CO*NH2:BeCl is 15 kJ·mol−1 larger than CO*OH:BeCl. Similarly, they are 51 kJ·mol−1 and 37 kJ·mol−1 larger for CO*OH:BeCl and CO*NH2:BeCl than for COO*H:BeCl and CON*H2:BeCl, respectively.
We previously showed in Figure 2 that the extra rings formed by the beryllium bonds may contain five members, six members and seven members in total. It is important, however, to keep in mind that a direct comparison between some of the five-member or six-member rings formed could be tricky (see Figure 5 as a suitable example). For the second subset of donors, COOH and CONH2, the ΔH1 values (not shown in Table 1, see Table S2), i.e., the differences between the conformers stabilized by an intramolecular beryllium bond and those that do not present this feature can be very high for six-member rings and reaches differences larger than one hundred kJ·mol−1 and thus showing the much larger nucleophilicity of the oxygen atom in the carbonyl group than that of the isolated OH group. Different kinds of five member and six member rings will be compared in the following section from the topological point of view.

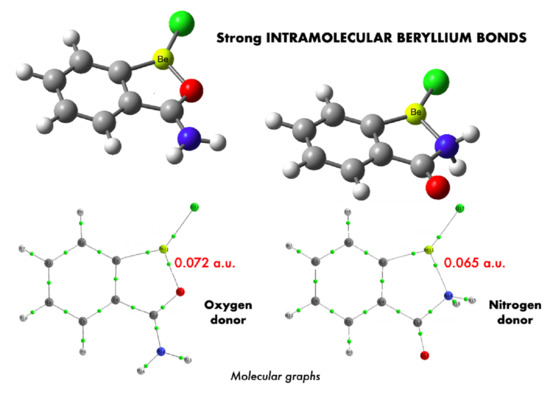
3.2. Nature of the Intramolecular Beryllium Bond

The electron density at the bond critical point (BCP) allows the comparison of the same kind of beryllium bond (O-Be, N-Be, P-Be and S-Be) in different structures. Figure 6, along with Figure S1 and Table S3 in the Supporting Information, summarizes the results for the electron density of the studied beryllium bonds culminated with the collection of molecular graphs.
The electron density ρ in Figure 6 shows at a glance the effect of the carbon chain and X at the beryllium acceptor (CH2)nBeX (n = 0, 1, 2; X = H, F, Cl) as well as the contrast between the different kinds of oxygens (black lines) and nitrogens (red lines) as donors. Firstly, it is important to note, as mentioned above, that no BCP is found for OH:BeX (X=H), SH:BeX and PH2:BeX (n = 0) derivatives, in agreement with the very low stabilization effects due essentially to van der Waals interactions found for this subset. It can be also observed that for donors OH, SH, NH2 and PH2, beryllium bonds forming five-member and six-member rings exhibit larger electron densities than four-member rings. For donors COOH and CONH2, five-member and six-member rings also have larger electron densities than seven-member rings. This is a well-known effect of geometry that is already described in proton-transfer processes in pyrazoles assisted by water where the optimum number is three and if a fourth water molecule is added the effect is worsened [60]. We confirm that Cl gives place to the highest values for the electron density; the strongest beryllium bond being that of CO*NH2:CH2BeCl. Regarding the Laplacian of the density, the values are positive, which is in agreement with typical ionic or closed shell interactions, and total energy densities are around zero or eventually slightly negative.
Typical strong beryllium bonds used to present [61] electron density values that correlate really well with the interatomic Y-Be distances according to an exponential fit (see Figure 7). This is the case we observe here for the strongest interactions (R2OH = 0.98 and R2NH2 = 0.98), while poorer donors exhibit poorer correlations (R2PH2 = 0.72 and R2SH = 0.78). Interactions through the carbonyl oxygen for both COOH and CONH2 groups present significantly shorter distances and a moderate correlation compared to larger beryllium bonds (R2CO* = 0.77), likely reflecting the stabilizing effects of the cyclization process. All correlation plots are shown in Figure S2.
For an easier comparison between O and N donor abilities and the influence of the sp2/sp3 character (which might be tricky, as pointed out before in Figure 5), in Figure 8 we focused on the effect on the beryllium bond electron density of these groups looking only at five-member and six-member rings of different kinds. As a suitable example, we selected (CH2)nBeCl substituents as acceptors. In this comparison, the ability of O as a donor increases in the order OH < COO*H < CO*OH < CO*NH2 and N is a better donor in the case of the amide group, although the difference between NH2 and CON*H2 is almost negligible on forming six-member rings. This might lead to the apparent conclusion that the sp2 character of lone pairs in carboxylic and amide groups makes them better donors towards beryllium.

3.3. Isodesmic Reactions

The NBO second-order interaction energies can only be used, strictly speaking, in relative terms. In order to have an energetic viewpoint on the intramolecular beryllium bonds that are investigated, we decided to use isodesmic reactions (see Scheme 2) which can provide some clues about the interaction between the donor and acceptor from a different perspective. Taking into account the conformational richness of the largest systems, we have analyzed the trends for the simplest n = 0 case (BeX as acceptor) for all donors since these are expected to present the lowest deformation energy values. In other words, the isodesmic energy (Eiso), as explained in the Computational details section, is decomposed in contributions arising from the interaction (Eint) and the deformation (Edef) of the reactants. Table 3 summarizes all these terms depending on the different donor–acceptor pairs.
Looking at the Eint column, we can immediately observe that the interaction energies increase in the order PH2 < SH < < OH < NH2 for the same BeX acceptor, which is in agreement with what we observed from the electron density results and the NBO second-order energies. This is not exactly the same trend observed when only looking at the stabilization energies in Table 1 because of the very low values obtained for OH. The explanation is also clear by looking at the values of the deformation energies, which are larger for OH than for NH2 and much larger than for SH or PH2, leading to isodesmic reactions for this donor that is smaller than the ones obtained for the other three since it was the also case for the stabilization energies.
Looking now to the CONH2 and COOH donors at the bottom of Table 3, we can also observe, for the same BeX acceptor, larger values for the carbonyl group in the former than in the latter, which is in agreement with a better nucleophilic character of the carbonyl oxygen in amides and that was already discussed in previous sections.
A second interesting trend is the acceptor ability of beryllium on the series BeH, BeF, BeCl. If we look at the Eint values (i.e., no deformation taken into account), we now find that interactions are always stronger along the H, F, Cl series and this is a trend that, again, is not exactly the same and is found neither in the stabilization energies (see Table 1) nor in the Eiso values, demonstrating again the role of the Edef term. In summary, although obtained differently, the interaction energy values extracted from the isodesmic scheme are in line with the second-order energies of the NBO method and the electron densities at the BCP, while the isodesmic energies are similar to the stabilization energies associated with the formation of the intramolecular beryllium bond in Table 1.

4. Conclusions

Intramolecular beryllium bonds are able to strongly stabilize 1,2-benzene derivatives, in particular, when forming five-membered or six-membered rings. In those cases, simple nitrogen (-NH2) and oxygen (-OH) donors give place to stabilization energies above 60 kJ·mol−1 and up to almost 90 kJ·mol−1 with respect to not bound conformers. The beryllium bonds have been characterized by the existence of a bond critical point of the electron density with positive Laplacian values and total energy density values around zero. Carbonyl oxygen and amide oxygen can give place to even larger electron density values. The acceptor ability of beryllium is increased when replacing hydrogen by halogen atoms. Interaction energies obtained with NBO and an isodesmic reaction scheme indicate that the intramolecular beryllium bond itself is very strong but a significant amount of energy is used in deforming the structure to fit into the newly formed ring. This is something that is particularly clear when looking at the angle formed between beryllium and its substituents, which is far from linearity (180°).

Supplementary Materials

The following are available, Table S1: Relative enthalpies at the M06-2X/6-31+G(d,p) level of theory, Table S2: Relative enthalpies at the M06-2X/6-311+G(d,p)//M06-2X/6-31+G(d,p) level of theory for the (CH2)nBeX:COOH not bound conformers with respect to the beryllium bond-containing ones, Table S3: Electron density at the beryllium bond BCP obtained at the M06-2X/6-311+G(d,p)//M062X/6-31+G(d,p) level of theory, Table S4: Second-order interaction energies obtained within the NBO approach between donors and the Be acceptor, Table S5: Cartesian coordinates for the Y:(CH2)nBeX 1,2-benzene derivatives (n = 0, 1, 2; X = H, F, Cl; Y = OH, NH2, SH, PH2, COOH, CONH2) optimized at the M06-2X/6-31+G(d,p) level of theory, Figure S1: Molecular graphs for the beryllium-bonded complexes at the M06-2X/6-311+G(d,p) level of theory. Values for the corresponding topological parameters are detailed in Table S3, Figure S2: Correlation between bond distances and electron energy densities for different donor groups.

Author Contributions

Conceptualization, M.Y. and J.E.; methodology, M.M.M.-C., I.A., and M.Y.; software, T.I.-T.; validation, M.M.M.-C., I.A., M.Y., and J.E.; formal analysis, M.M.M.-C., I.A., and M.Y.; investigation, M.M.M.-C., I.A., M.Y., and J.E.; resources, I.A. and M.Y.; data curation, T.I.-T. and M.M.M.-C.; writing—original draft preparation, M.Y.; writing—review and editing, M.M.M.-C., I.A., M.Y., and J.E.; visualization, M.M.M.-C.; supervision, M.Y. and J.E.; project administration, I.A. and M.Y.; funding acquisition, I.A. and M.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was carried out with financial support from the Ministerio de Ciencia, Innovación y Universidades of Spain (Project No. PGC2018-094644-B-C21 and PGC2018–094644-B-C22).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in the article and in the Supplementary Material.

Acknowledgments

This work was carried out with financial support from the projects PGC2018-094644-B-C21, PGC2018-094644-B-C22 of the Ministerio de Ciencia, Innovación y Universidades of Spain. Gratitude is also given to the CTI (CSIC) the Centro de Computación Científica of the UAM (CCC-UAM) for the generous allocation of computer time and for their continued technical support. We also thank Professor Otilia Mó for very helpful discussions.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Van der Waals, J.D. On the Continuity of the Gaseous and Liquid States. Ph.D. Thesis, Hoogeschool te Leiden, Leiden, The Netherlands. Edited by J. S. Rowlinson. Dover Phoenix Ed.: New York, NY, USA, 2004.
  2. Muller-Dethlefs, K.; Hobza, P. Noncovalent interactions: A challenge for experiment and theory. Chem. Rev. 2000, 100, 143–167. [Google Scholar] [CrossRef]
  3. Dill, K.A. Dominant forces in protein folding. Biochemistry 1990, 29, 7133–7155. [Google Scholar] [CrossRef] [PubMed]
  4. Newberry, R.W.; Raines, R.T. Secondary Forces in Protein Folding. ACS Chem. Biol. 2019, 14, 1677–1686. [Google Scholar] [CrossRef] [PubMed]
  5. Uddin, M.A.; Lee, T.H.; Xu, S.; Park, S.Y.; Kim, T.; Song, S.; Nguyen, T.L.; Ko, S.J.; Hwang, S.; Kim, J.Y.; et al. Interplay of Intramolecular Noncovalent Coulomb Interactions for Semicrystalline Photovoltaic Polymers. Chem. Mater. 2015, 27, 5997–6007. [Google Scholar] [CrossRef]
  6. Pauling, L. The Shared-Electron Chemical Bond. Proc. Nat. Acad. Sci. USA 1929, 14, 359–362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Pauling, L. The Nature of the Chemical Bond; Cornell University Press: Ithaca, NY, USA, 1939. [Google Scholar]
  8. Pauling, L. The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
  9. Alkorta, I.; Elguero, J.; Frontera, A. Not only hydrogen bonds: Other noncovalent interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef] [Green Version]
  10. Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef]
  11. Yao, W.B.; Crabtree, R.H. An eta(1)-aldehyde complex and the role of hydrogen bonding in its conversion to an eta(1)-imine complex. Inorg. Chem. 1996, 35, 3007–3011. [Google Scholar] [CrossRef]
  12. Alkorta, I.; Elguero, J.; Foces-Foces, C. Dihydrogen bonds (A-H ··· H-B). Chem. Commun. 1996, 14, 1633–1634. [Google Scholar] [CrossRef]
  13. Yáñez, M.; Sanz, P.; Mó, O.; Alkorta, I.; Elguero, J. Beryllium Bonds, do they exist? J. Chem. Theor. Comput. 2009, 5, 2763–2771. [Google Scholar] [CrossRef]
  14. Yang, X.; Li, Q.Z.; Cheng, J.B.; Li, W.Z. A new interaction mechanism of LiNH2 with MgH2: Magnesium bond. J. Mol. Model. 2013, 19, 247–253. [Google Scholar] [CrossRef]
  15. Costa, P.; Mieres-Perez, J.; Ozkan, N.; Sander, W. Activation of the B-F Bond by Diphenylcarbene: A Reversible 1,2-Fluorine Migration between Boron and Carbon. Angew. Chem. Int. Ed. 2017, 56, 1760–1764. [Google Scholar] [CrossRef]
  16. Grabowski, S.J. Boron and other Triel Lewis Acid Centers: From Hypovalency to Hypervalency. Chemphyschem 2014, 15, 2985–2993. [Google Scholar] [CrossRef] [PubMed]
  17. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
  18. Zahn, S.; Frank, R.; Hey-Hawkins, E.; Kirchner, B. Pnicogen Bonds: A New Molecular Linker? Chem. A Eur. J. 2011, 17, 6034–6038. [Google Scholar] [CrossRef] [PubMed]
  19. Del Bene, J.E.; Alkorta, I.; Elguero, J. The Pnicogen Bond in Review: Structures, Binding Energies, Bonding Properties, and Spin-Spin Coupling Constants of Complexes Stabilized by Pnicogen Bonds. In Noncovalent Forces; Scheiner, S., Ed.; Springer International Publisher: Cham, Germany, 2015; pp. 191–263. [Google Scholar]
  20. Wang, W.Z.; Ji, B.M.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef] [PubMed]
  21. Metrangolo, P.; Resnati, G. Halogen bonding: A paradigm in supramolecular chemistry. Chem. Eur. J. 2001, 7, 2511–2519. [Google Scholar] [CrossRef]
  22. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other s-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
  23. Montero-Campillo, M.M.; Alkorta, I.; Elguero, J. Fostering the Basic Instinct of Boron in Boron-Beryllium Interactions. J. Phys. Chem. A 2018, 122, 3313–3319. [Google Scholar] [CrossRef] [PubMed]
  24. Martín-Sómer, A.; Montero-Campillo, M.M.; Mó, O.; Yáñez, M.; Alkorta, I.; Elguero, J. Some Interesting Features of Non-Covalent Interactions. Croat. Chem. Acta 2014, 87, 291–306. [Google Scholar] [CrossRef]
  25. Hurtado, M.; Yáñez, M.; Herrero, R.; Guerrero, A.; Dávalos, J.Z.; Abboud, J.-L.M.; Khater, B.; Guillemin, J.C. The Ever-Surprising Boron Chemistry. Enhanced Acidity of Phosphine-boranes. Chem. Eur. J. 2009, 15, 4622–4629. [Google Scholar] [CrossRef] [PubMed]
  26. Martín-Fernández, C.; Montero-Campillo, M.M.; Alkorta, I.; Yáñez, M.; Mó, O.; Elguero, J. Large Proton-Affinity Enhancements Triggered by Noncovalent Interactions. Chem. Eur. J. 2018, 24, 1971–1977. [Google Scholar] [CrossRef]
  27. Brea, O.; Alkorta, I.; Corral, I.; Mó, O.; Yáñez, M.; Elguero, J. Intramolecular Beryllium Bonds. Further Insights into Resonance Asistance Phenomena. In Intermolecular Interactions in Crystals: Fundamentals of Crystal Engineering; Novoa, J.J., Ed.; The Royal Society of Chemistry: London, UK, 2018. [Google Scholar]
  28. Sanz, P.; Montero-Campillo, M.M.; Mó, O.; Yáñez, M.; Alkorta, I.; Elguero, J. Intramolecular magnesium bonds in malonaldehyde-like systems: A critical view of the resonance-assisted phenomena. Theor. Chem. Acc. 2018, 137, 97. [Google Scholar] [CrossRef] [Green Version]
  29. Foti, M.C.; Barclay, L.R.C.; Ingold, K.U. The role of hydrogen bonding on the H-atom-donating abilities of catechols and naphthalene diols and on a previously overlooked aspect of their infrared spectra. J. Am. Chem. Soc. 2002, 124, 12881–12888. [Google Scholar] [CrossRef]
  30. Kjaergaard, H.G.; Howard, D.L.; Schofield, D.P.; Robinson, T.W.; Ishiuchi, S.; Fujii, M. OH- and CH-stretching overtone spectra of catechol. J. Phys. Chem. A 2002, 106, 258–266. [Google Scholar] [CrossRef]
  31. Hunt, N.T.; Turner, A.R.; Wynne, K. Inter- and intramolecular hydrogen bonding in phenol derivatives: A model system for poly-L-tyrosine. J. Phys. Chem. B 2005, 109, 19008–19017. [Google Scholar] [CrossRef]
  32. Varfolomeev, M.A.; Abaidullina, D.I.; Gainutdinova, A.Z.; Solomonov, B.N. FTIR study of H-bonds cooperativity in complexes of 1,2-dihydroxybenzene with proton acceptors in aprotic solvents: Influence of the intramolecular hydrogen bond. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2010, 77, 965–972. [Google Scholar] [CrossRef] [PubMed]
  33. Vedernikova, I.; Proynov, E.; Salahub, D.; Haemers, A. Local atomic and orbital reactivity indices from density functional calculations for hydrogen-bonded 1,2-dihydroxybenzene. Int. J. Quantum Chem. 2000, 77, 161–173. [Google Scholar] [CrossRef]
  34. Rozas, I.; Alkorta, I.; Elguero, J. Intramolecular hydrogen bonds in ortho-substituted hydroxybenzenes and in 8-susbtituted 1-hydroxynaphthalenes: Can a methyl group be an acceptor of hydrogen bonds? J. Phys. Chem. A 2001, 105, 10462–10467. [Google Scholar] [CrossRef]
  35. Zhang, H.Y.; Sung, Y.M.; Wang, X.L. Substituent effects on O-H bond dissociation enthalpies and ionization potentials of catechols: A DFT study and its implications in the rational design of phenolic antioxidants and elucidation of structure-Activity relationships for flavonoid antioxidants. Chem. Eur. J. 2003, 9, 502–508. [Google Scholar] [CrossRef]
  36. Mandado, M.; Graña, A.M.; Mosquera, R.A. Do 1,2-ethanediol and 1,2-dihydroxybenzene present intramolecular hydrogen bond? Phys. Chem. Chem. Phys. 2004, 6, 4391–4396. [Google Scholar] [CrossRef]
  37. Gu, J.D.; Wang, J.; Leszczynski, J.; Xie, Y.M.; Schaefer III, H.F. To stack or not to stack: Performance of a new density functional for the uracil and thymine dimers. Chem. Phys. Lett. 2008, 459, 164–166. [Google Scholar] [CrossRef]
  38. Frisch, M.J.T.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  39. Keith, T.A. AIMAll (Version 19.10.12); TK Gristmill Software: Overland Park, KS, USA, 2019. [Google Scholar]
  40. Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
  41. Boto, R.A.; Peccati, F.; Laplaza, R.; Quan, C.; Carbone, A.; Piquemal, J.P.; Maday, Y.; Contreras-García, J. Fast, Robust, and Quantitative Analysis of Noncovalent Interactions. J. Chem. Theory Comput. 2020, 16, 4150–4158. [Google Scholar] [CrossRef]
  42. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  43. Song, J.W.; Tsuneda, T.; Sato, T.; Hirao, K. Calculations of alkane energies using long-range corrected DFT combined with intramolecular van der waals correlation. Org. Lett. 2010, 12, 1440–1443. [Google Scholar] [CrossRef]
  44. Snitsiriwat, S.; Bozzelli, J.W. Thermochemical properties for isooctane and carbon radicals: Computational study. J. Phys. Chem. A 2013, 117, 421–429. [Google Scholar] [CrossRef]
  45. Sánchez-Sanz, G.; Alkorta, I.; Trujillo, C.; Elguero, J. Intramolecular pnicogen interactions in PHF-(CH2) n-PHF (n=2-6) systems. ChemPhysChem 2013, 14, 1656–1665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. Mezei, P.D.; Csonka, G.I.; Ruzsinszky, A.; Kállay, M. Construction and Application of a New Dual-Hybrid Random Phase Approximation. J. Chem. Theory Comput. 2015, 11, 4615–4626. [Google Scholar] [CrossRef] [PubMed]
  47. Channar, P.A.; Saeed, A.; Larik, F.A.; Flörke, U.; El-Seedi, H.; Rodríguez Pirani, L.S.; Erben, M.F. An intramolecular 1,5-chalcogen bond on the conformational preference of carbonyl thiocarbamate species. New J. Chem. 2020, 44, 5243–5253. [Google Scholar] [CrossRef]
  48. Kovács, A.; Hargittai, I. Hydrogen-bonding interactions of the trifluoromethyl group: 2-Trifluoromethylvinyl alcohol. Int. J. Quant. Chem. 1997, 62, 645–652. [Google Scholar] [CrossRef]
  49. Howard, S.T.; Abernethy, C.D. Intramolecular C-H...Ccarbene Hydrogen Bonds and Competing Interactions in Monoprotonated Tripodal Carbenes. J. Comput. Chem. 2004, 25, 649–659. [Google Scholar] [CrossRef]
  50. Sanz, P.; Mó, O.; Yáñez, M.; Elguero, J. Bonding in Tropolone, 2-Aminotropone and Aminotroponimine. No Evidence of Resonance Assisted Hydrogen Bond (RAHB) Effects. Chem. Eur. J. 2008, 14, 4225–4232. [Google Scholar] [CrossRef]
  51. Rosado, M.T.S.; Jesus, A.J.L.; Reva, I.D.; Fausto, R.; Redinha, J.S. Conformational cooling dynamics in matrix-isolated 1,3-butanediol. J. Phys. Chem. A 2009, 113, 7499–7507. [Google Scholar] [CrossRef] [Green Version]
  52. Jesus, A.J.L.; Redinha, J.S. Conformational study of charged cyclohexyldiamines and their gas phase acid-base properties. Struct. Chem. 2011, 22, 999–1006. [Google Scholar] [CrossRef]
  53. Zhang, L.; Li, D. An insight into intramolecular blue-shifting C–H⋯π hydrogen bonds in 1,3-hexadien-5-yne and its halogen-substituted derivatives. Chem. Phys. 2019, 518, 58–68. [Google Scholar] [CrossRef]
  54. Bickelhaupt, F.M.; Houk, K.N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  55. Johansson, A.; Kollman, P.; Rothenberg, S.; McKelvey, J. Hydrogen Bonding Ability of the Amide Group. J. Am. Chem. Soc. 1974, 96, 3794–3800. [Google Scholar] [CrossRef]
  56. Emsley, J.; Hoyte, O.P.A.; Overill, R.E. Ab Initio Calculations on the Very Strong Hydrogen Bond of the Biformate Anion and Comparative Esterification Studies. J. Am. Chem. Soc. 1978, 100, 3303–3306. [Google Scholar] [CrossRef]
  57. Ewbank, J.D.; Klimkowski, V.J.; Siam, K.; Schäfer, L. Conformational analysis of the methyl ester of alanine by gas electron diffraction and Ab initio geometry optimization. J. Mol. Struct. 1987, 160, 275–285. [Google Scholar] [CrossRef]
  58. Wu, J.; Lebrilla, C.B. Gas-Phase Basicities and Sites of Protonation of Glycine Oligomers (GLYn; n = 1–5). J. Am. Chem. Soc. 1993, 115, 3270–3275. [Google Scholar] [CrossRef]
  59. Mikshiev, V.Y.; Pozharskii, A.F.; Filarowski, A.; Novikov, A.S.; Antonov, A.S.; Tolstoy, P.M.; Vovk, M.A.; Khoroshilova, O.V. How Strong is Hydrogen Bonding to Amide Nitrogen? ChemPhysChem 2020, 21, 651–658. [Google Scholar] [CrossRef] [PubMed]
  60. Oziminski, W.P. The kinetics of water-assisted tautomeric 1,2-proton transfer in azoles: A computational approach. Struct. Chem. 2016, 27, 1845–1854. [Google Scholar] [CrossRef] [Green Version]
  61. Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Universal features of the electron density distribution in hydrogen- bonding regions: A comprehensive study involving H···X (X=H, C, N, O, F, S, Cl, π) interactions. Chem. Eur. J. 2010, 16, 2442–2452. [Google Scholar] [CrossRef] [PubMed]
Molecules 26 03401 sch001 550
Scheme 1. Ortho-substituted benzene derivatives studied including a Be moiety as a Lewis acid that is capable of forming intramolecular beryllium bonds.
Scheme 1. Ortho-substituted benzene derivatives studied including a Be moiety as a Lewis acid that is capable of forming intramolecular beryllium bonds.
Molecules 26 03401 sch001
Molecules 26 03401 sch002 550
Scheme 2. Isodesmic reactions used to estimate the intramolecular interaction energy due to the beryllium bonds exemplified for the particular case of carbon chains with n = 0 (see Scheme 1).
Scheme 2. Isodesmic reactions used to estimate the intramolecular interaction energy due to the beryllium bonds exemplified for the particular case of carbon chains with n = 0 (see Scheme 1).
Molecules 26 03401 sch002
Molecules 26 03401 g001 550
Figure 1. (a) Meaning of enthalpy ΔH1 taking NH2:BeCl as a suitable example. Enthalpy ΔH1 gives the stabilization provided by the formation of a beryllium bond. (b) Meaning of enthalpy ΔH2 taking COOH:CH2BeCl as a suitable example. Enthalpy ΔH2 gives the energy difference depending on the binding site for a same donor. The color code for the atoms is the following: hydrogen: white; carbon: grey; nitrogen: blue; oxygen: red; chlorine: green; and beryllium: yellow.
Figure 1. (a) Meaning of enthalpy ΔH1 taking NH2:BeCl as a suitable example. Enthalpy ΔH1 gives the stabilization provided by the formation of a beryllium bond. (b) Meaning of enthalpy ΔH2 taking COOH:CH2BeCl as a suitable example. Enthalpy ΔH2 gives the energy difference depending on the binding site for a same donor. The color code for the atoms is the following: hydrogen: white; carbon: grey; nitrogen: blue; oxygen: red; chlorine: green; and beryllium: yellow.
Molecules 26 03401 g001
Molecules 26 03401 g002 550
Figure 2. Suitable examples of the global minima where the formation of the intramolecular beryllium bond leads to the formation of an extra four-(NH2:BeH), five-(NH2:CH2BeH), six-(NH2:C2H4BeH) or seven-(CONH2:C2H4BeH) membered heterocycle. The atoms color code is the same as in Figure 1.
Figure 2. Suitable examples of the global minima where the formation of the intramolecular beryllium bond leads to the formation of an extra four-(NH2:BeH), five-(NH2:CH2BeH), six-(NH2:C2H4BeH) or seven-(CONH2:C2H4BeH) membered heterocycle. The atoms color code is the same as in Figure 1.
Molecules 26 03401 g002
Molecules 26 03401 g003 550
Figure 3. NCI plot for the PH2:BeCl structure showing the weak interaction between the donor and acceptor (green-colored isosurface) and a slightly red-colored region denoting a certain connection between the four atoms susceptible of forming a ring through a BeB.
Figure 3. NCI plot for the PH2:BeCl structure showing the weak interaction between the donor and acceptor (green-colored isosurface) and a slightly red-colored region denoting a certain connection between the four atoms susceptible of forming a ring through a BeB.
Molecules 26 03401 g003
Molecules 26 03401 g004 550
Figure 4. Molecular graphs for CO*OH:BeCl, COO*H:BeCl, CO*NH2:BeCl and CON*H2:BeCl derivatives showing the electron density (au) (red color) at the intramolecular beryllium bond.
Figure 4. Molecular graphs for CO*OH:BeCl, COO*H:BeCl, CO*NH2:BeCl and CON*H2:BeCl derivatives showing the electron density (au) (red color) at the intramolecular beryllium bond.
Molecules 26 03401 g004
Molecules 26 03401 g005 550
Figure 5. Comparison between different kinds of five-member rings depending on the donor (OH and COO*H). The same applies for larger rings. Distances are provided in Å.
Figure 5. Comparison between different kinds of five-member rings depending on the donor (OH and COO*H). The same applies for larger rings. Distances are provided in Å.
Molecules 26 03401 g005
Molecules 26 03401 g006 550
Figure 6. Electron density values (au) according to substitution patterns for ortho-substituted benzenes. The number of (CH2) groups in the different systems is indicated in the X axis.
Figure 6. Electron density values (au) according to substitution patterns for ortho-substituted benzenes. The number of (CH2) groups in the different systems is indicated in the X axis.
Molecules 26 03401 g006
Molecules 26 03401 g007 550
Figure 7. Exponential correlation between the Be-O distance and the density values at the bond critical point for the whole -OH series.
Figure 7. Exponential correlation between the Be-O distance and the density values at the bond critical point for the whole -OH series.
Molecules 26 03401 g007
Molecules 26 03401 g008 550
Figure 8. Comparison of density values for the pairs between (CH2)nBeX, where X = Cl and O, N donors for the formation of five-member and six-member rings of different kinds (see Figure 2).
Figure 8. Comparison of density values for the pairs between (CH2)nBeX, where X = Cl and O, N donors for the formation of five-member and six-member rings of different kinds (see Figure 2).
Molecules 26 03401 g008
Table
Table 1. M06-2X/6-311+G(d,p)//M06-2X/6-31+G(d,p) relative enthalpies ΔH1 (kJ·mol−1) between the beryllium bound conformer and the most stable non-bound conformer, taking the beryllium bound conformer as zero. At the bottom of the table and for substituents COOH and CONH2, the enthalpy difference, ΔH2 (kJ·mol−1), between the two possible conformers exhibiting a beryllium bond, the one involving the carbonyl group (systematically the most stable) and the one involving the OH (NH2) group, is given.
Table 1. M06-2X/6-311+G(d,p)//M06-2X/6-31+G(d,p) relative enthalpies ΔH1 (kJ·mol−1) between the beryllium bound conformer and the most stable non-bound conformer, taking the beryllium bound conformer as zero. At the bottom of the table and for substituents COOH and CONH2, the enthalpy difference, ΔH2 (kJ·mol−1), between the two possible conformers exhibiting a beryllium bond, the one involving the carbonyl group (systematically the most stable) and the one involving the OH (NH2) group, is given.
ΔH1AcceptorBeHCH2BeHC2H4BeHBeFCH2BeFC2H4BeFBeClCH2BeClC2H4BeCl
Donor
OH2.260.461.86.759.962.57.167.671.0
SH12.541.835.811.340.932.511.747.839.8
NH223.169.674.526.873.674.331.381.087.0
PH24.421.826.41.620.221.91.426.329.9
ΔH2AcceptorBeHCH2BeHC2H4BeHBeFCH2BeFC2H4BeFBeClCH2BeClC2H4BeCl
Donor
COOH14.828.025.219.030.624.718.831.827.9
CONH251.353.950.556.257.654.154.157.256.4
Table
Table 2. Be-Y distances (Å, Y atom donor of the Lewis base) and C-Be-X angle (italic characters) for the ortho-substituted benzenes considered in Scheme 1. Stars on COOH and CONH2 donors indicate which donor atom is involved in the interaction.
Table 2. Be-Y distances (Å, Y atom donor of the Lewis base) and C-Be-X angle (italic characters) for the ortho-substituted benzenes considered in Scheme 1. Stars on COOH and CONH2 donors indicate which donor atom is involved in the interaction.
Molecules 26 03401 i001
BeHCH2BeHC2H4BeHBeFCH2BeFC2H4BeFBeClCH2BeClC2H4BeCl
OH1.838
159.4		1.695
149.1		1.694
146.4		1.830
159.7		1.710
149.4		1.703
146.8		1.794
157.7		1.679
148.0		1.672
144.2
SH2.727
168.9		2.241
149.2		2.246
147.1		2.648
166.4		2.290
149.9		2.311
148.1		2.487
160.6		2.228
145.9		2.232
143.3
NH21.855
154.6		1.787
145.5		1.794
141.7		1.847
154.7		1.796
145.2		1.796
142.1		1.819
153.7		1.769
144.0		1.767
139.7
PH23.007
172.5		2.310
146.4		2.280
142.6		2.987
171.3		2.365
147.8		2.353
144.2		2.984
170.1		2.285
143.4		2.266
139.9
CO*OH
COO*H		1.697
143.3
1.690
148.8		1.650
137.0
1.674
144.8		1.690
138.6
1.740
144.9		1.694
143.3
1.701
149.0		1.652
138.0
1.681
145.2		1.693
138.0
1.742
145.4		1.675
141.6
1.676
147.2		1.631
135.7
1.685
142.8		1.663
135.8
1.710
141.1
CO*NH2
CON*H2		1.660
141.5
1.773
144.4		1.635
136.5
1.779
140.4		1.660
135.8
1.828
142.2		1.657
141.3
1.779
144.5		1.633
136.8
1.787
140.7		1.662
135.1
1.832
142.3		1.639
139.8
1.751
142.7		1.613
140.7
1.761
138.4		1.636
133.2
1.797
139.3
Table
Table 3. Isodesmic energies (Eiso), interaction energies (Eint) and deformation energies (Edef) for the different compounds at the M06-2X/6-311+G(d,p) level of theory. For COOH and CONH2 groups, the first line corresponds to O(CO) and the second line corresponds to OH/NH2.
Table 3. Isodesmic energies (Eiso), interaction energies (Eint) and deformation energies (Edef) for the different compounds at the M06-2X/6-311+G(d,p) level of theory. For COOH and CONH2 groups, the first line corresponds to O(CO) and the second line corresponds to OH/NH2.
Interacting Pairs EisoEintEdef
OHBeH−6.1−86.680.5
BeF−9.0−99.190.1
BeCl−10.6−103.993.3
NH2BeH−49.7−128.178.4
BeF−53.6−143.089.3
BeCl−59.2−148.289.0
SHBeH−13.7−29.315.7
BeF−14.3−37.423.0
BeCl−15.7−53.137.4
PH2BeH−7.4−11.84.4
BeF−7.9−13.25.3
BeCl−8.4−13.55.2
COOHBeH−82.6−166.383.7
−66.1−130.964.8
BeF−85.1−173.488.3
−64.3−129.765.4
BeCl−91.2−182.791.5
−70.4−141.471.0
CONH2BeH−111.2−198.186.9
−59.5−168.4109.0
BeF−114.1−206.692.5
−57.9−172.8114.9
BeCl−122.2−216.994.7
−67.8−189.8122.0
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

I-Ting, T.; Montero-Campillo, M.M.; Alkorta, I.; Elguero, J.; Yáñez, M. Large Stabilization Effects by Intramolecular Beryllium Bonds in Ortho-Benzene Derivatives. Molecules 2021, 26, 3401. https://doi.org/10.3390/molecules26113401

AMA Style

I-Ting T, Montero-Campillo MM, Alkorta I, Elguero J, Yáñez M. Large Stabilization Effects by Intramolecular Beryllium Bonds in Ortho-Benzene Derivatives. Molecules. 2021; 26(11):3401. https://doi.org/10.3390/molecules26113401

Chicago/Turabian Style

I-Ting, Tsai, M. Merced Montero-Campillo, Ibon Alkorta, José Elguero, and Manuel Yáñez. 2021. "Large Stabilization Effects by Intramolecular Beryllium Bonds in Ortho-Benzene Derivatives" Molecules 26, no. 11: 3401. https://doi.org/10.3390/molecules26113401

APA Style

I-Ting, T., Montero-Campillo, M. M., Alkorta, I., Elguero, J., & Yáñez, M. (2021). Large Stabilization Effects by Intramolecular Beryllium Bonds in Ortho-Benzene Derivatives. Molecules, 26(11), 3401. https://doi.org/10.3390/molecules26113401

Article Metrics

Back to TopTop