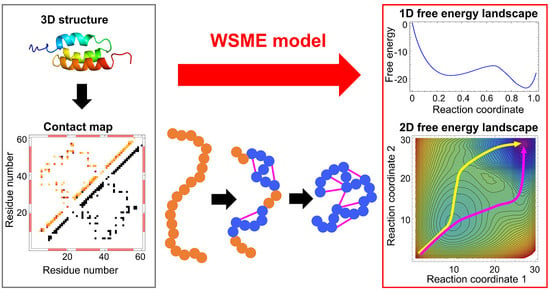
The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics
Abstract
:1. Introduction
2. WSME Model
2.1. Description of the Model
2.2. Calculation of the Partition Function
2.3. Contact Energy
3. Prediction of Folding Mechanisms
3.1. One-Dimensional Free-Energy Landscape: Two-State Versus Downhill Folding
3.2. Two-Dimensional Free-Energy Landscape: Multiple Folding Pathways
3.3. Effects of Amino-Acid Substitutions on Stability and Folding
3.4. Effects of External Forces on Protein (un)Folding
3.5. Folding Kinetics and Transition State
4. Folding Mechanisms of Multi-Domain Proteins
4.1. Tandem Connection of Multiple Domains
4.2. Domain Insertions
5. Applications beyond Protein Folding
5.1. Intrinsically Disordered Proteins
5.2. Conformational Changes Associated with Protein Function
5.3. Other Applications
6. Summary and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Levinthal, C. How to fold graciously. In Mössbauer Spectroscopy in Biological Systems, Proceedings of the Meeting Held at Allerton House, Monticello, IL, USA, 17–18 March 1969; Department of Chemistry and Physics, University of Illinois: Champaign, IL, USA, 1969; Volume 67, pp. 22–24. [Google Scholar]
- Dobson, C.M.; Evans, P.A.; Radford, S.E. Understanding how proteins fold: The lysozyme story so far. Trends Biochem. Sci. 1994, 19, 31–37. [Google Scholar] [CrossRef]
- Jackson, S.E. How do small single-domain proteins fold? Fold. Des. 1998, 3, R81–R91. [Google Scholar] [CrossRef] [Green Version]
- Arai, M.; Kuwajima, K. Role of the molten globule state in protein folding. Adv. Protein Chem. 2000, 53, 209–282. [Google Scholar] [CrossRef]
- Arai, M. Unified understanding of folding and binding mechanisms of globular and intrinsically disordered proteins. Biophys. Rev. 2018, 10, 163–181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Šali, A.; Shakhnovich, E.; Karplus, M. How does a protein fold? Nature 1994, 369, 248–251. [Google Scholar] [CrossRef]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef] [Green Version]
- Dill, K.A.; Bromberg, S.; Yue, K.; Fiebig, K.M.; Yee, D.P.; Thomas, P.D.; Chan, H.S. Principles of protein folding—A perspective from simple exact models. Protein Sci. 1995, 4, 561–602. [Google Scholar] [CrossRef] [Green Version]
- Dobson, C.M.; Šali, A.; Karplus, M. Protein folding: A perspective from theory and experiment. Angew. Chem. Int. Ed. 1998, 37, 868–893. [Google Scholar] [CrossRef]
- Mayor, U.; Guydosh, N.R.; Johnson, C.M.; Grossmann, J.G.; Sato, S.; Jas, G.S.; Freund, S.M.; Alonso, D.O.; Daggett, V.; Fersht, A.R. The complete folding pathway of a protein from nanoseconds to microseconds. Nature 2003, 421, 863–867. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How fast-folding proteins fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef]
- Dill, K.A.; Ozkan, S.B.; Shell, M.S.; Weikl, T.R. The protein folding problem. Annu. Rev. Biophys. 2008, 37, 289–316. [Google Scholar] [CrossRef]
- Muñoz, V.; Eaton, W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11311–11316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alm, E.; Baker, D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11305–11310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galzitskaya, O.V.; Finkelstein, A.V. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc. Natl. Acad. Sci. USA 1999, 96, 11299–11304. [Google Scholar] [CrossRef] [Green Version]
- Onuchic, J.N.; Wolynes, P.G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004, 14, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Sasai, M.; Chikenji, G.; Terada, T.P. Cooperativity and modularity in protein folding. Biophys. Phys. 2016, 13, 281–293. [Google Scholar] [CrossRef] [Green Version]
- Wako, H.; Saitô, N. Statistical mechanical theory of the protein conformation. I. General considerations and the application to homopolymers. J. Phys. Soc. Jpn. 1978, 44, 1931–1938. [Google Scholar] [CrossRef]
- Wako, H.; Saitô, N. Statistical mechanical theory of the protein conformation. II. Folding pathway for protein. J. Phys. Soc. Jpn. 1978, 44, 1939–1945. [Google Scholar] [CrossRef]
- Bruscolini, P.; Pelizzola, A. Exact solution of the Muñoz-Eaton model for protein folding. Phys. Rev. Lett. 2002, 88, 258101. [Google Scholar] [CrossRef] [Green Version]
- Gopi, S.; Devanshu, D.; Krishna, P.; Naganathan, A.N. pStab: Prediction of stable mutants, unfolding curves, stability maps and protein electrostatic frustration. Bioinformatics 2018, 34, 875–877. [Google Scholar] [CrossRef] [Green Version]
- Gopi, S.; Devanshu, D.; Rajasekaran, N.; Anantakrishnan, S.; Naganathan, A.N. pPerturb: A server for predicting long-distance energetic couplings and mutation-induced stability changes in proteins via perturbations. ACS Omega 2020, 5, 1142–1146. [Google Scholar] [CrossRef] [PubMed]
- Gō, N.; Abe, H. Non-interacting local-structure model of folding and unfolding transition in globular-proteins. 1. Formulation. Biopolymers 1981, 20, 991–1011. [Google Scholar] [CrossRef] [PubMed]
- Gō, N. Theoretical studies of protein folding. Annu. Rev. Biophys. Bioeng. 1983, 12, 183–210. [Google Scholar] [CrossRef]
- Takada, S. Gō-ing for the prediction of protein folding mechanisms. Proc. Natl. Acad. Sci. USA 1999, 96, 11698–11700. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Itoh, K.; Sasai, M. Flexibly varying folding mechanism of a nearly symmetrical protein: B domain of protein A. Proc. Natl. Acad. Sci. USA 2006, 103, 7298–7303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyazawa, S.; Jernigan, R.L. Most probable intermediates in protein folding-unfolding with a noninteracting globule-coil model. Biochemistry 1982, 21, 5203–5213. [Google Scholar] [CrossRef] [PubMed]
- Abe, H.; Gō, N. Non-interacting local-structure model of folding and unfolding transition in globular-proteins. 2. Application to two-dimensional lattice proteins. Biopolymers 1981, 20, 1013–1031. [Google Scholar] [CrossRef] [PubMed]
- Saitô, N. Statistical-mechanics of DNA and protein suitable for computer calculation. Cell Biophys. 1987, 11, 321–329. [Google Scholar] [CrossRef]
- Matouschek, A.; Kellis, J.T., Jr.; Serrano, L.; Fersht, A.R. Mapping the transition state and pathway of protein folding by protein engineering. Nature 1989, 340, 122–126. [Google Scholar] [CrossRef]
- Fersht, A.R.; Matouschek, A.; Serrano, L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 1992, 224, 771–782. [Google Scholar] [CrossRef]
- Fersht, A.R.; Sato, S. Φ-value analysis and the nature of protein-folding transition states. Proc. Natl. Acad. Sci. USA 2004, 101, 7976–7981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Udgaonkar, J.B.; Baldwin, R.L. NMR evidence for an early framework intermediate on the folding pathway of ribonuclease A. Nature 1988, 335, 694–699. [Google Scholar] [CrossRef]
- Roder, H.; Elöve, G.A.; Englander, S.W. Structural characterization of folding intermediates in cytochrome c by H-exchange labelling and proton NMR. Nature 1988, 335, 700–704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radford, S.E.; Dobson, C.M.; Evans, P.A. The folding of hen lysozyme involves partially structured intermediates and multiple pathways. Nature 1992, 358, 302–307. [Google Scholar] [CrossRef] [PubMed]
- Jennings, P.A.; Wright, P.E. Formation of a molten globule intermediate early in the kinetic folding pathway of apomyoglobin. Science 1993, 262, 892–896. [Google Scholar] [CrossRef] [PubMed]
- Henry, E.R.; Eaton, W.A. Combinatorial modeling of protein folding kinetics: Free energy profiles and rates. Chem. Phys. 2004, 307, 163–185. [Google Scholar] [CrossRef]
- Cellmer, T.; Henry, E.R.; Kubelka, J.; Hofrichter, J.; Eaton, W.A. Relaxation rate for an ultrafast folding protein is independent of chemical denaturant concentration. J. Am. Chem. Soc. 2007, 129, 14564–14565. [Google Scholar] [CrossRef]
- Cellmer, T.; Henry, E.R.; Hofrichter, J.; Eaton, W.A. Measuring internal friction of an ultrafast-folding protein. Proc. Natl. Acad. Sci. USA 2008, 105, 18320–18325. [Google Scholar] [CrossRef] [Green Version]
- Godoy-Ruiz, R.; Henry, E.R.; Kubelka, J.; Hofrichter, J.; Muñoz, V.; Sanchez-Ruiz, J.M.; Eaton, W.A. Estimating free-energy barrier heights for an ultrafast folding protein from calorimetric and kinetic data. J. Phys. Chem. B 2008, 112, 5938–5949. [Google Scholar] [CrossRef] [Green Version]
- Kubelka, J.; Henry, E.R.; Cellmer, T.; Hofrichter, J.; Eaton, W.A. Chemical, physical, and theoretical kinetics of an ultrafast folding protein. Proc. Natl. Acad. Sci. USA 2008, 105, 18655–18662. [Google Scholar] [CrossRef] [Green Version]
- Henry, E.R.; Best, R.B.; Eaton, W.A. Comparing a simple theoretical model for protein folding with all-atom molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17880–17885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, J.K.; Kubelka, G.S.; Kubelka, J. Sequence, structure, and cooperativity in folding of elementary protein structural motifs. Proc. Natl. Acad. Sci. USA 2015, 112, 9890–9895. [Google Scholar] [CrossRef] [Green Version]
- Lai, J.K.; Kubelka, G.S.; Kubelka, J. Effect of mutations on the global and site-specific stability and folding of an elementary protein structural motif. J. Phys. Chem. B 2018, 122, 11083–11094. [Google Scholar] [CrossRef] [PubMed]
- Inanami, T.; Terada, T.P.; Sasai, M. Folding pathway of a multidomain protein depends on its topology of domain connectivity. Proc. Natl. Acad. Sci. USA 2014, 111, 15969–15974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flammini, A.; Banavar, J.R.; Maritan, A. Energy landscape and native-state structure of proteins—A simplified model. Eur. Lett. 2002, 58, 623–629. [Google Scholar] [CrossRef]
- Liang, K.K.; Hayashi, M.; Shiu, Y.J.; Mo, Y.; Shao, J.S.; Yan, Y.J.; Lin, S.H. Thermodynamics and kinetics of protein folding: A mean field theory. Phys. Chem. Chem. Phys. 2003, 5, 5300–5308. [Google Scholar] [CrossRef]
- Garcia-Mira, M.M.; Sadqi, M.; Fischer, N.; Sanchez-Ruiz, J.M.; Muñoz, V. Experimental identification of downhill protein folding. Science 2002, 298, 2191–2195. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.; Jung, Y. Calculations of free energy surfaces for small proteins and a protein-RNA complex using a lattice model approach. Bull. Korean Chem. Soc. 2011, 32, 3051–3056. [Google Scholar] [CrossRef] [Green Version]
- Zamparo, M.; Pelizzola, A. Kinetics of the Wako-Saitô-Muñoz-Eaton model of protein folding. Phys. Rev. Lett. 2006, 97, 068106. [Google Scholar] [CrossRef] [Green Version]
- Bruscolini, P.; Pelizzola, A.; Zamparo, M. Downhill versus two-state protein folding in a statistical mechanical model. J. Chem. Phys. 2007, 126, 215103. [Google Scholar] [CrossRef] [Green Version]
- Zamparo, M.; Pelizzola, A. Nearly symmetrical proteins: Folding pathways and transition states. J. Chem. Phys. 2009, 131, 035101. [Google Scholar] [CrossRef] [PubMed]
- Faccin, M.; Bruscolini, P.; Pelizzola, A. Analysis of the equilibrium and kinetics of the ankyrin repeat protein myotrophin. J. Chem. Phys. 2011, 134, 075102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radford, S.E.; Dobson, C.M.; Dobson, C.M.; Fersht, A.R. Insights into protein folding using physical techniques: Studies of lysozyme and α-lactalbumin. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1995, 348, 17–25. [Google Scholar] [CrossRef]
- Mizuguchi, M.; Arai, M.; Ke, Y.; Nitta, K.; Kuwajima, K. Equilibrium and kinetics of the folding of equine lysozyme studied by circular dichroism spectroscopy. J. Mol. Biol. 1998, 283, 265–277. [Google Scholar] [CrossRef] [PubMed]
- McCallister, E.L.; Alm, E.; Baker, D. Critical role of β-hairpin formation in protein G folding. Nat. Struct. Biol. 2000, 7, 669–673. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, T.K.; Arai, M.; Terada, T.P.; Ikura, T.; Kuwajima, K. Equilibrium and kinetic studies on folding of the authentic and recombinant forms of human α-lactalbumin by circular dichroism spectroscopy. Biochemistry 2000, 39, 15643–15651. [Google Scholar] [CrossRef] [PubMed]
- Karanicolas, J.; Brooks, C.L., 3rd. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002, 11, 2351–2361. [Google Scholar] [CrossRef] [Green Version]
- Schlepckow, K.; Wirmer, J.; Bachmann, A.; Kiefhaber, T.; Schwalbe, H. Conserved folding pathways of α-lactalbumin and lysozyme revealed by kinetic CD, fluorescence, NMR, and interrupted refolding experiments. J. Mol. Biol. 2008, 378, 686–698. [Google Scholar] [CrossRef]
- Nakamura, T.; Makabe, K.; Tomoyori, K.; Maki, K.; Mukaiyama, A.; Kuwajima, K. Different folding pathways taken by highly homologous proteins, goat α-lactalbumin and canine milk lysozyme. J. Mol. Biol. 2010, 396, 1361–1378. [Google Scholar] [CrossRef]
- Yu, W.; Chung, K.; Cheon, M.; Heo, M.; Han, K.H.; Ham, S.; Chang, I. Cooperative folding kinetics of BBL protein and peripheral subunit-binding domain homologues. Proc. Natl. Acad. Sci. USA 2008, 105, 2397–2402. [Google Scholar] [CrossRef] [Green Version]
- Halskau, O.; Perez-Jimenez, R.; Ibarra-Molero, B.; Underhaug, J.; Muñoz, V.; Martinez, A.; Sanchez-Ruiz, J.M. Large-scale modulation of thermodynamic protein folding barriers linked to electrostatics. Proc. Natl. Acad. Sci. USA 2008, 105, 8625–8630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naganathan, A.N. Predictions from an Ising-like statistical mechanical model on the dynamic and thermodynamic effects of protein surface electrostatics. J. Chem. Theory Comput. 2012, 8, 4646–4656. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Shin, Y.-K.; Yoon, J.-Y.; Nam, K.-H.; Munashingha, P.R.; Park, S.; Park, S.-Y.; Kim, S.; Lee, J.; Seo, M.J.; et al. Computational design of a thermolabile uracil-DNA glycosylase of Escherichia coli. Biophys. J. 2022, 121, 1276–1288. [Google Scholar] [CrossRef]
- Bruscolini, P.; Naganathan, A.N. Quantitative prediction of protein folding behaviors from a simple statistical model. J. Am. Chem. Soc. 2011, 133, 5372–5379. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Yuan, J.M.; Teranishi, Y.; Lin, S.H. Thermodynamics of protein folding using a modified Wako-Saitô-Muñoz-Eaton model. J. Biol. Phys. 2012, 38, 543–571. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Kim, S.; Jung, Y.; Han, J.; Yun, J.H.; Chang, I.; Lee, W. Probing the folding-unfolding transition of a thermophilic protein, MTH1880. PLoS ONE 2016, 11, e0145853. [Google Scholar] [CrossRef] [PubMed]
- Naganathan, A.N.; Orozco, M. The conformational landscape of an intrinsically disordered DNA-binding domain of a transcription regulator. J. Phys. Chem. B 2013, 117, 13842–13850. [Google Scholar] [CrossRef]
- Naganathan, A.N.; Muñoz, V. Thermodynamics of downhill folding: Multi-probe analysis of PDD, a protein that folds over a marginal free energy barrier. J. Phys. Chem. B 2014, 118, 8982–8994. [Google Scholar] [CrossRef]
- Naganathan, A.N.; Perez-Jimenez, R.; Muñoz, V.; Sanchez-Ruiz, J.M. Estimation of protein folding free energy barriers from calorimetric data by multi-model Bayesian analysis. Phys. Chem. Chem. Phys. 2011, 13, 17064–17076. [Google Scholar] [CrossRef]
- Rajasekaran, N.; Gopi, S.; Narayan, A.; Naganathan, A.N. Quantifying protein disorder through measures of excess conformational entropy. J. Phys. Chem. B 2016, 120, 4341–4350. [Google Scholar] [CrossRef]
- Gopi, S.; Singh, A.; Suresh, S.; Paul, S.; Ranu, S.; Naganathan, A.N. Toward a quantitative description of microscopic pathway heterogeneity in protein folding. Phys. Chem. Chem. Phys. 2017, 19, 20891–20903. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, S.; Golla, H.; Divakar, K.; Kannan, A.; de Sancho, D.; Naganathan, A.N. Slow folding of a helical protein: Large barriers, strong internal friction, or a shallow, bumpy landscape? J. Phys. Chem. B 2020, 124, 8973–8983. [Google Scholar] [CrossRef] [PubMed]
- Munshi, S.; Naganathan, A.N. Imprints of function on the folding landscape: Functional role for an intermediate in a conserved eukaryotic binding protein. Phys. Chem. Chem. Phys. 2015, 17, 11042–11052. [Google Scholar] [CrossRef] [PubMed]
- Sivanandan, S.; Naganathan, A.N. A disorder-induced domino-like destabilization mechanism governs the folding and functional dynamics of the repeat protein IκBα. PLoS Comput. Biol. 2013, 9, e1003403. [Google Scholar] [CrossRef] [Green Version]
- Jurrus, E.; Engel, D.; Star, K.; Monson, K.; Brandi, J.; Felberg, L.E.; Brookes, D.H.; Wilson, L.; Chen, J.; Liles, K.; et al. Improvements to the APBS biomolecular solvation software suite. Protein Sci. 2018, 27, 112–128. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharjee, K.; Gopi, S.; Naganathan, A.N. A disordered loop mediates heterogeneous unfolding of an ordered protein by altering the native ensemble. J. Phys. Chem. Lett. 2020, 11, 6749–6756. [Google Scholar] [CrossRef]
- Itoh, K.; Sasai, M. Multidimensional theory of protein folding. J. Chem. Phys. 2009, 130, 145104. [Google Scholar] [CrossRef] [Green Version]
- Chung, H.S.; Tokmakoff, A. Temperature-de pendent downhill unfolding of ubiquitin. II. Modeling the free energy surface. Proteins 2008, 72, 488–497. [Google Scholar] [CrossRef]
- Garniz-Arco, G.; Risso, V.A.; Gaucher, E.A.; Gavira, J.A.; Naganathan, A.N.; Ibarra-Molero, B.; Sanchez-Ruiz, J.M. Combining ancestral reconstruction with folding-landscape simulations to engineer heterologous protein expression. J. Mol. Biol. 2021, 433, 167321. [Google Scholar] [CrossRef]
- Naganathan, A.N.; Dani, R.; Gopi, S.; Aranganathan, A.; Narayan, A. Folding intermediates, heterogeneous native ensembles and protein function. J. Mol. Biol. 2021, 433, 167325. [Google Scholar] [CrossRef]
- Sato, S.; Religa, T.L.; Daggett, V.; Fersht, A.R. Testing protein-folding simulations by experiment: B domain of protein A. Proc. Natl. Acad. Sci. USA 2004, 101, 6952–6956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sato, S.; Fersht, A.R. Searching for multiple folding pathways of a nearly symmetrical protein: Temperature dependent Φ-value analysis of the B domain of protein A. J. Mol. Biol. 2007, 372, 254–267. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, N.; Naganathan, A.N. A self-consistent structural perturbation approach for determining the magnitude and extent of allosteric coupling in proteins. Biochem. J. 2017, 474, 2379–2388. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, N.; Suresh, S.; Gopi, S.; Raman, K.; Naganathan, A.N. A general mechanism for the propagation of mutational effects in proteins. Biochemistry 2017, 56, 294–305. [Google Scholar] [CrossRef]
- Garg, S.; Sagar, A.; Singaraju, G.S.; Dani, R.; Bari, N.K.; Naganathan, A.N.; Rakshit, S. Weakening of interaction networks with aging in tip-link protein induces hearing loss. Biochem. J. 2021, 478, 121–134. [Google Scholar] [CrossRef]
- Gopi, S.; Rajasekaran, N.; Singh, A.; Ranu, S.; Naganathan, A.N. Energetic and topological determinants of a phosphorylation-induced disorder-to-order protein conformational switch. Phys. Chem. Chem. Phys. 2015, 17, 27264–27269. [Google Scholar] [CrossRef]
- Naganathan, A.N.; Sanchez-Ruiz, J.M.; Munshi, S.; Suresh, S. Are protein folding intermediates the evolutionary consequence of functional constraints? J. Phys. Chem. B 2015, 119, 1323–1333. [Google Scholar] [CrossRef]
- Naganathan, A.N. Molecular origins of folding rate differences in the thioredoxin family. Biochem. J. 2020, 477, 1083–1087. [Google Scholar] [CrossRef] [Green Version]
- Narayan, A.; Gopi, S.; Lukose, B.; Naganathan, A.N. Electrostatic frustration shapes folding mechanistic differences in paralogous bacterial stress response proteins. J. Mol. Biol. 2020, 432, 4830–4839. [Google Scholar] [CrossRef]
- Naganathan, A.N.; Kannan, A. A hierarchy of coupling free energies underlie the thermodynamic and functional architecture of protein structures. Curr. Res. Struct. Biol. 2021, 3, 257–267. [Google Scholar] [CrossRef]
- Golla, H.; Kannan, A.; Gopi, S.; Murugan, S.; Perumalsamy, L.R.; Naganathan, A.N. Structural–energetic basis for coupling between equilibrium fluctuations and phosphorylation in a protein native ensemble. ACS Cent. Sci. 2022, 8, 282–293. [Google Scholar] [CrossRef]
- Imparato, A.; Pelizzola, A.; Zamparo, M. Ising-like model for protein mechanical unfolding. Phys. Rev. Lett. 2007, 98, 148102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imparato, A.; Pelizzola, A.; Zamparo, M. Protein mechanical unfolding: A model with binary variables. J. Chem. Phys. 2007, 127, 145105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caraglio, M.; Imparato, A.; Pelizzola, A. Pathways of mechanical unfolding of FnIII(10): Low force intermediates. J. Chem. Phys. 2010, 133, 065101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imparato, A.; Pelizzola, A. Mechanical unfolding and refolding pathways of ubiquitin. Phys. Rev. Lett. 2008, 100, 158104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caraglio, M.; Imparato, A.; Pelizzola, A. Direction-dependent mechanical unfolding and green fluorescent protein as a force sensor. Phys. Rev. E 2011, 84, 021918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imparato, A.; Pelizzola, A.; Zamparo, M. Equilibrium properties and force-driven unfolding pathways of RNA molecules. Phys. Rev. Lett. 2009, 103, 188102. [Google Scholar] [CrossRef] [Green Version]
- Ancona, M.; Bentivoglio, A.; Caraglio, M.; Gonnella, G.; Pelizzola, A. Emergence of effective temperatures in an out-of-equilibrium model of biopolymer folding. Phys. Rev. E 2021, 103, 062415. [Google Scholar] [CrossRef]
- Aioanei, D.; Tessari, I.; Bubacco, L.; Samori, B.; Brucale, M. Observing the osmophobic effect in action at the single molecule level. Proteins 2011, 79, 2214–2223. [Google Scholar] [CrossRef]
- Aioanei, D.; Brucale, M.; Tessari, I.; Bubacco, L.; Samori, B. Worm-like Ising model for protein mechanical unfolding under the effect of osmolytes. Biophys. J. 2012, 102, 342–350. [Google Scholar] [CrossRef] [Green Version]
- Caraglio, M.; Pelizzola, A. Effects of confinement on thermal stability and folding kinetics in a simple Ising-like model. Phys. Biol. 2012, 9, 016006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pelizzola, A.; Zamparo, M. Nonequilibrium dynamics of an exactly solvable Ising-like model and protein translocation. Eur. Lett. 2013, 102, 10001. [Google Scholar] [CrossRef] [Green Version]
- Bruscolini, P.; Pelizzola, A.; Zamparo, M. Rate determining factors in protein model structures. Phys. Rev. Lett. 2007, 99, 038103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niewieczerzal, S.; Cieplak, M. The folding transition state theory in simple model systems. J. Phys. Condens. Matter 2008, 20, 244134. [Google Scholar] [CrossRef]
- Narayan, A.; Naganathan, A.N. Evidence for the sequential folding mechanism in RNase H from an ensemble-based model. J. Phys. Chem. B 2014, 118, 5050–5058. [Google Scholar] [CrossRef]
- Chang, I.; Cieplak, M.; Banavar, J.R.; Maritan, A. What can one learn from experiments about the elusive transition state? Protein Sci. 2004, 13, 2446–2457. [Google Scholar] [CrossRef] [Green Version]
- Itoh, K.; Sasai, M. Cooperativity, connectivity, and folding pathways of multidomain proteins. Proc. Natl. Acad. Sci. USA 2008, 105, 13865–13870. [Google Scholar] [CrossRef] [Green Version]
- Wako, H.; Abe, H. Characterization of protein folding by a Φ-value calculation with a statistical-mechanical model. Biophys. Phys. 2016, 13, 263–279. [Google Scholar] [CrossRef] [Green Version]
- Gopi, S.; Paul, S.; Ranu, S.; Naganathan, A.N. Extracting the hidden distributions underlying the mean transition state structures in protein folding. J. Phys. Chem. Lett. 2018, 9, 1771–1777. [Google Scholar] [CrossRef]
- Gopi, S.; Naganathan, A.N. Non-specific DNA-driven quinary interactions promote structural transitions in proteins. Phys. Chem. Chem. Phys. 2020, 22, 12671–12677. [Google Scholar] [CrossRef]
- Gopi, S.; Lukose, B.; Naganathan, A.N. Diverse native ensembles dictate the differential functional responses of nuclear receptor ligand-binding domains. J. Phys. Chem. B 2021, 125, 3546–3555. [Google Scholar] [CrossRef] [PubMed]
- Hutton, R.D.; Wilkinson, J.; Faccin, M.; Sivertsson, D.M.; Pelizzola, A.; Lowe, A.R.; Bruscolini, P.; Itzhaki, L.S. Mapping the topography of a protein energy landscape. J. Am. Chem. Soc. 2015, 137, 14610–14625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gopi, S.; Aranganathan, A.; Naganathan, A.N. Thermodynamics and folding landscapes of large proteins from a statistical mechanical model. Curr. Res. Struct. Biol. 2019, 1, 6–12. [Google Scholar] [CrossRef]
- Pacheco-Garcia, J.L.; Anoz-Carbonell, E.; Vankova, P.; Kannan, A.; Palomino-Morales, R.; Mesa-Torres, N.; Salido, E.; Man, P.; Medina, M.; Naganathan, A.N.; et al. Structural basis of the pleiotropic and specific phenotypic consequences of missense mutations in the multifunctional NAD(P)H:quinone oxidoreductase 1 and their pharmacological rescue. Redox Biol. 2021, 46, 102112. [Google Scholar] [CrossRef] [PubMed]
- Sannigrahi, A.; Chowdhury, S.; Das, B.; Banerjee, A.; Halder, A.; Kumar, A.; Saleem, M.; Naganathan, A.N.; Karmakar, S.; Chattopadhyay, K. The metal cofactor zinc and interacting membranes modulate SOD1 conformation-aggregation landscape in an in vitro ALS model. eLife 2021, 10, e61453. [Google Scholar] [CrossRef] [PubMed]
- Apic, G.; Gough, J.; Teichmann, S.A. Domain combinations in archaeal, eubacterial and eukaryotic proteomes. J. Mol. Biol. 2001, 310, 311–325. [Google Scholar] [CrossRef] [Green Version]
- Han, J.H.; Batey, S.; Nickson, A.A.; Teichmann, S.A.; Clarke, J. The folding and evolution of multidomain proteins. Nat. Rev. Mol. Cell Biol. 2007, 8, 319–330. [Google Scholar] [CrossRef]
- Aroul-Selvam, R.; Hubbard, T.; Sasidharan, R. Domain insertions in protein structures. J. Mol. Biol. 2004, 338, 633–641. [Google Scholar] [CrossRef] [Green Version]
- Touchette, N.A.; Perry, K.M.; Matthews, C.R. Folding of dihydrofolate reductase from Escherichia coli. Biochemistry 1986, 25, 5445–5452. [Google Scholar] [CrossRef]
- Fersht, A.R. The sixth Datta Lecture. Protein folding and stability: The pathway of folding of barnase. FEBS Lett. 1993, 325, 5–16. [Google Scholar] [CrossRef] [Green Version]
- Jennings, P.A.; Finn, B.E.; Jones, B.E.; Matthews, C.R. A reexamination of the folding mechanism of dihydrofolate reductase from Escherichia coli: Verification and refinement of a four-channel model. Biochemistry 1993, 32, 3783–3789. [Google Scholar] [CrossRef] [PubMed]
- Jones, B.E.; Matthews, C.R. Early intermediates in the folding of dihydrofolate reductase from Escherichia coli detected by hydrogen exchange and NMR. Protein Sci. 1995, 4, 167–177. [Google Scholar] [CrossRef] [Green Version]
- Arai, M.; Kuwajima, K. Rapid formation of a molten globule intermediate in refolding of α-lactalbumin. Fold. Des. 1996, 1, 275–287. [Google Scholar] [CrossRef] [Green Version]
- Arai, M.; Hamel, P.; Kanaya, E.; Inaka, K.; Miki, K.; Kikuchi, M.; Kuwajima, K. Effect of an alternative disulfide bond on the structure, stability, and folding of human lysozyme. Biochemistry 2000, 39, 3472–3479. [Google Scholar] [CrossRef] [PubMed]
- Arai, M.; Ito, K.; Inobe, T.; Nakao, M.; Maki, K.; Kamagata, K.; Kihara, H.; Amemiya, Y.; Kuwajima, K. Fast compaction of α-lactalbumin during folding studied by stopped-flow X-ray scattering. J. Mol. Biol. 2002, 321, 121–132. [Google Scholar] [CrossRef]
- Arai, M.; Maki, K.; Takahashi, H.; Iwakura, M. Testing the relationship between foldability and the early folding events of dihydrofolate reductase from Escherichia coli. J. Mol. Biol. 2003, 328, 273–288. [Google Scholar] [CrossRef]
- Arai, M.; Kataoka, M.; Kuwajima, K.; Matthews, C.R.; Iwakura, M. Effects of the difference in the unfolded-state ensemble on the folding of Escherichia coli dihydrofolate reductase. J. Mol. Biol. 2003, 329, 779–791. [Google Scholar] [CrossRef]
- Arai, M.; Iwakura, M. Probing the interactions between the folding elements early in the folding of Escherichia coli dihydrofolate reductase by systematic sequence perturbation analysis. J. Mol. Biol. 2005, 347, 337–353. [Google Scholar] [CrossRef]
- Arai, M.; Kondrashkina, E.; Kayatekin, C.; Matthews, C.R.; Iwakura, M.; Bilsel, O. Microsecond hydrophobic collapse in the folding of Escherichia coli dihydrofolate reductase, an α/β-type protein. J. Mol. Biol. 2007, 368, 219–229. [Google Scholar] [CrossRef]
- Arai, M.; Iwakura, M.; Matthews, C.R.; Bilsel, O. Microsecond subdomain folding in dihydrofolate reductase. J. Mol. Biol. 2011, 410, 329–342. [Google Scholar] [CrossRef]
- Muñoz, V. A simple theoretical model goes a long way in explaining complex behavior in protein folding. Proc. Natl. Acad. Sci. USA 2014, 111, 15863–15864. [Google Scholar] [CrossRef] [Green Version]
- Wright, P.E.; Dyson, H.J. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunker, A.; Lawson, J.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef] [Green Version]
- Arai, M.; Sugase, K.; Dyson, H.J.; Wright, P.E. Conformational propensities of intrinsically disordered proteins influence the mechanism of binding and folding. Proc. Natl. Acad. Sci. USA 2015, 112, 9614–9619. [Google Scholar] [CrossRef] [Green Version]
- Matsushita, K.; Kikuchi, M. Frustration-induced protein intrinsic disorder. J. Chem. Phys. 2013, 138, 105101. [Google Scholar] [CrossRef]
- Matsushita, K.; Kikuchi, M. Short polypeptide with metastable structures. Interdiscip. Sci. Rev. 2013, 19, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Matsushita, K.; Kikuchi, M. Multicanonical simulation of coupled folding and binding of intrinsically disordered protein using an Ising-like protein model. J. Phys. Conf. Ser. 2013, 454, 012034. [Google Scholar] [CrossRef] [Green Version]
- Munshi, S.; Gopi, S.; Asampille, G.; Subramanian, S.; Campos, L.A.; Atreya, H.S.; Naganathan, A.N. Tunable order-disorder continuum in protein-DNA interactions. Nucleic Acids Res. 2018, 46, 8700–8709. [Google Scholar] [CrossRef] [Green Version]
- Rajendran, D.; Mitra, S.; Oikawa, H.; Madhurima, K.; Sekhar, A.; Takahashi, S.; Naganathan, A.N. Quantification of entropic excluded volume effects driving crowding-induced collapse and folding of a disordered protein. J. Phys. Chem. Lett. 2022, 13, 3112–3120. [Google Scholar] [CrossRef]
- Munshi, S.; Rajendran, D.; Naganathan, A.N. Entropic control of an excited folded-like conformation in a disordered protein ensemble. J. Mol. Biol. 2018, 430, 2688–2694. [Google Scholar] [CrossRef]
- Munshi, S.; Rajendran, D.; Ramesh, S.; Subramanian, S.; Bhattacharjee, K.; Kumar, M.R.; Naganathan, A.N. Controlling structure and dimensions of a disordered protein via mutations. Biochemistry 2020, 59, 171–174. [Google Scholar] [CrossRef] [PubMed]
- Itoh, K.; Sasai, M. Coupling of functioning and folding: Photoactive yellow protein as an example system. Chem. Phys. 2004, 307, 121–127. [Google Scholar] [CrossRef]
- Itoh, K.; Sasai, M. Dynamical transition and proteinquake in photoactive yellow protein. Proc. Natl. Acad. Sci. USA 2004, 101, 14736–14741. [Google Scholar] [CrossRef] [Green Version]
- Itoh, K.; Sasai, M. Entropic mechanism of large fluctuation in allosteric transition. Proc. Natl. Acad. Sci. USA 2010, 107, 7775–7780. [Google Scholar] [CrossRef] [Green Version]
- Itoh, K.; Sasai, M. Statistical mechanics of protein allostery: Roles of backbone and side-chain structural fluctuations. J. Chem. Phys. 2011, 134, 125102. [Google Scholar] [CrossRef] [PubMed]
- Hellingwerf, K.J.; Hendriks, J.; Gensch, T. Photoactive yellow protein, a new type of photoreceptor protein: Will this “yellow lab” bring us where we want to go? J. Phys. Chem. A 2003, 107, 1082–1094. [Google Scholar] [CrossRef] [Green Version]
- Narayan, A.; Campos, L.A.; Bhatia, S.; Fushman, D.; Naganathan, A.N. Graded structural polymorphism in a bacterial thermosensor protein. J. Am. Chem. Soc. 2017, 139, 792–802. [Google Scholar] [CrossRef] [PubMed]
- Narayan, A.; Naganathan, A.N. Tuning the continuum of structural states in the native ensemble of a regulatory protein. J. Phys. Chem. Lett. 2017, 8, 1683–1687. [Google Scholar] [CrossRef] [Green Version]
- Narayan, A.; Naganathan, A.N. Switching protein conformational substates by protonation and mutation. J. Phys. Chem. B 2018, 122, 11039–11047. [Google Scholar] [CrossRef] [Green Version]
- Chiti, F.; Dobson, C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006, 75, 333–366. [Google Scholar] [CrossRef] [Green Version]
- Iadanza, M.G.; Jackson, M.P.; Hewitt, E.W.; Ranson, N.A.; Radford, S.E. A new era for understanding amyloid structures and disease. Nat. Rev. Mol. Cell Biol. 2018, 19, 755–773. [Google Scholar] [CrossRef]
- Zamparo, M.; Trovato, A.; Maritan, A. Simplified exactly solvable model for β-amyloid aggregation. Phys. Rev. Lett. 2010, 105, 108102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, X.H.; Wu, M.C. Simplified lattice model for polypeptide fibrillar transitions. Phys. Rev. E 2014, 90, 042701. [Google Scholar] [CrossRef] [PubMed]
- Tokar, V.I.; Dreysse, H. A model of strained epitaxy on an alloyed substrate. J. Phys. Condens. Matter 2004, 16, S2203–S2210. [Google Scholar] [CrossRef]
- Tokar, V.I.; Dreysse, H. Transfer matrix solution of the Wako-Saitô-Muñoz-Eaton model augmented by arbitrary short range interactions. J. Stat. Mech. 2010, 2010, P08028. [Google Scholar] [CrossRef]
- Pelizzola, A. Exactness of the cluster variation method and factorization of the equilibrium probability for the Wako-Saitô-Muñoz-Eaton model of protein folding. J. Stat. Mech. 2005, 2005, P11010. [Google Scholar] [CrossRef] [Green Version]
- Pelizzola, A. Cluster variation method in statistical physics and probabilistic graphical models. J. Phys. A Math. Theory 2005, 38, R309–R339. [Google Scholar] [CrossRef]
- Zamparo, M.; Pelizzola, A. Rigorous results on the local equilibrium kinetics of a protein folding model. J. Stat. Mech. 2006, 2006, P12009. [Google Scholar] [CrossRef]
- Lee, J. Exact partition function zeros of the Wako-Saitô-Muñoz-Eaton β hairpin model. Phys. Rev. E 2013, 88, 022710. [Google Scholar] [CrossRef] [Green Version]
- Lee, J. Exact partition function zeros of the Wako-Saitô-Muñoz-Eaton protein model. Phys. Rev. Lett. 2013, 110, 248101. [Google Scholar] [CrossRef] [Green Version]
- Lee, J. Phase diagram of the Wako-Saitô-Muñoz-Eaton β hairpin model obtained from the partition-function zeros. J. Korean Phys. Soc. 2014, 65, 671–675. [Google Scholar] [CrossRef] [Green Version]
- Lee, J. Finite-size phase diagram of the Wako-Saitô-Muñoz-Eaton α-helix model. J. Korean Phys. Soc. 2015, 67, 1187–1191. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Outeiral, C.; Nissley, D.A.; Deane, C.M. Current structure predictors are not learning the physics of protein folding. Bioinformatics 2022, 38, 1881–1887. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ooka, K.; Liu, R.; Arai, M. The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics. Molecules 2022, 27, 4460. https://doi.org/10.3390/molecules27144460
Ooka K, Liu R, Arai M. The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics. Molecules. 2022; 27(14):4460. https://doi.org/10.3390/molecules27144460
Chicago/Turabian StyleOoka, Koji, Runjing Liu, and Munehito Arai. 2022. "The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics" Molecules 27, no. 14: 4460. https://doi.org/10.3390/molecules27144460
APA StyleOoka, K., Liu, R., & Arai, M. (2022). The Wako-Saitô-Muñoz-Eaton Model for Predicting Protein Folding and Dynamics. Molecules, 27(14), 4460. https://doi.org/10.3390/molecules27144460