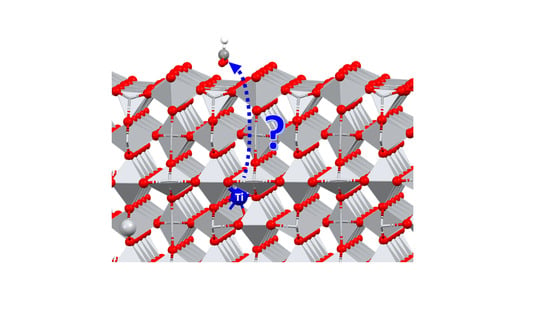
Effect of Formic Acid on the Outdiffusion of Ti Interstitials at TiO2 Surfaces: A DFT+U Investigation
Abstract
:1. Introduction
2. Results
2.1. Adsorption of Formic Acid at the Undefected Surfaces
2.2. Sites for Excess Ti Atoms at the Rutile Surface
2.3. Adsorption of Formic Acid at the Ti-Rich TiO2(110) Surface
2.4. Sites for Excess Ti Atoms at the Anatase Surface
2.5. Adsorption of Formic Acid at the Ti-Rich a-TiO2(101) Surface
3. Discussion
4. Computational Methods and Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wandelt, K. Properties and Influence of Surface Defects. Surf. Sci. 1991, 251–252, 387–395. [Google Scholar] [CrossRef]
- Chen, X.; Mao, S.S. Titanium Dioxide Nanomaterials: Synthesis, Properties, Modifications, and Applications. Chem. Rev. 2007, 107, 2891–2959. [Google Scholar] [CrossRef]
- Danish, M.S.S.; Bhattacharya, A.; Stepanova, D.; Mikhaylov, A.; Grilli, M.L.; Khosravy, M.; Senjyu, T. A Systematic Review of Metal Oxide Applications for Energy and Environmental Sustainability. Metals 2020, 10, 1604. [Google Scholar] [CrossRef]
- Kazachenko, A.; Vasilieva, N.; Fetisova, O.; Sychev, V.; Elsuf’ev, E.; Malyar, Y.; Issaoui, N.; Miroshnikova, A.; Borovkova, V.; Kazachenko, A.; et al. New Reactions of Betulin with Sulfamic Acid and Ammonium Sulfamate in the Presence of Solid Catalysts. Biomass Convers. Biorefinery 2022, 1265, 133394. [Google Scholar] [CrossRef]
- Bennett, R.A.; McCavish, N.D. Non-Stoichiometric Oxide Surfaces and Ultra-Thin Films: Characterisation of TiO2. Top. Catal. 2005, 36, 11–19. [Google Scholar] [CrossRef]
- Finazzi, E.; Di Valentin, C.; Pacchioni, G. Nature of Ti Interstitials in Reduced Bulk Anatase and Rutile TiO2. J. Phys. Chem. C 2009, 113, 3382–3385. [Google Scholar] [CrossRef]
- Mulheran, P.A.; Nolan, M.; Browne, C.S.; Basham, M.; Sanvillee, E.; Bennett, R.A. Surface and Interstitial Ti Diffusion at the Rutile TiO2(110) Surface. Phys. Chem. Chem. Phys. 2010, 12, 9763–9771. [Google Scholar] [CrossRef] [Green Version]
- Tanner, A.J.; Wen, B.; Ontaneda, J.; Zhang, Y.; Grau-Crespo, R.; Fielding, H.H.; Selloni, A.; Thornton, G. Polaron-Adsorbate Coupling at the TiO2(110)-Carboxylate Interface. J. Phys. Chem. Lett. 2021, 12, 3571–3576. [Google Scholar] [CrossRef]
- Yoon, Y.; Du, Y.; Garcia, J.C.; Zhu, Z.; Wang, Z.-T.; Petrik, N.G.; Kimmel, G.A.; Dohnalek, Z.; Henderson, M.A.; Rousseau, R.; et al. Anticorrelation between Surface and Subsurface Point Defects and the Impact on the Redox Chemistry of TiO2(110). ChemPhysChem 2015, 16, 313–321. [Google Scholar] [CrossRef]
- Xia, G.-J.; Lee, M.-S.; Glezakou, V.-A.; Rousseau, R.; Wang, Y.-G. Diffusion and Surface Segregation of Interstitial Ti Defects Induced by Electronic Metal–Support Interactions on a Au/TiO2 Nanocatalyst. ACS Catal. 2022, 12, 4455–4464. [Google Scholar] [CrossRef]
- Kremer, M.K.; Forrer, D.; Rogero, C.; Floreano, L.; Vittadini, A. Digging Ti Interstitials at the R-TiO2(110) Surface: Mechanism of Porphyrin Ti Sequestration by Iminic N Nucleophilic Attack. Appl. Surf. Sci. 2021, 564, 150403. [Google Scholar] [CrossRef]
- Koebl, J.; Wang, T.; Wang, C.; Drost, M.; Tu, F.; Xu, Q.; Ju, H.; Wechsler, D.; Franke, M.; Pan, H.; et al. Hungry Porphyrins: Protonation and Self-Metalation of Tetraphenylporphyrin on TiO2(110)-1 × 1. ChemistrySelect 2016, 1, 6103–6105. [Google Scholar] [CrossRef]
- Lovat, G.; Forrer, D.; Abadia, M.; Dominguez, M.; Casarin, M.; Rogero, C.; Vittadini, A.; Floreano, L. On-Surface Synthesis of a Pure and Long-Range-Ordered Titanium(IV)-Porphyrin Contact Layer on Titanium Dioxide. J. Phys. Chem. C 2017, 121, 13738–13746. [Google Scholar] [CrossRef]
- Bates, S.P.; Kresse, G.; Gillan, M.J. The Adsorption and Dissociation of ROH Molecules on TiO2(110). Surf. Sci. 1998, 409, 336–349. [Google Scholar] [CrossRef]
- Chambers, S.A.; Henderson, M.A.; Kim, Y.J.; Thevuthasan, S. Chemisorption Geometry, Vibrational Spectra, and Thermal Desorption of Formic Acid on TiO2(110). Surf. Rev. Lett. 1998, 5, 381–385. [Google Scholar] [CrossRef]
- Hayden, B.E.; King, A.; Newton, M.A. Fourier Transform Reflection−Absorption IR Spectroscopy Study of Formate Adsorption on TiO2(110). J. Phys. Chem. B 1999, 103, 203–208. [Google Scholar] [CrossRef]
- Vittadini, A.; Selloni, A.; Rotzinger, F.P.; Grätzel, M. Formic Acid Adsorption on Dry and Hydrated TiO2 Anatase (101) Surfaces by DFT Calculations. J. Phys. Chem. B 2000, 104, 1300–1306. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, B.; Dahal, A.; Kimmel, G.A.; Rousseau, R.; Selloni, A.; Petrik, N.G.; Dohnálek, Z. Binding of Formic Acid on Anatase TiO2(101). J. Phys. Chem. C 2020, 124, 20228–20239. [Google Scholar] [CrossRef]
- Kwon, S.; Lin, T.C.; Iglesia, E. Elementary Steps and Site Requirements in Formic Acid Dehydration Reactions on Anatase and Rutile TiO2 Surfaces. J. Catal. 2020, 383, 60–76. [Google Scholar] [CrossRef]
- Tabacchi, G.; Fabbiani, M.; Mino, L.; Martra, G.; Fois, E. The Case of Formic Acid on Anatase TiO2(101): Where Is the Acid Proton? Angew. Chem. Int. Ed. 2019, 58, 12431–12434. [Google Scholar] [CrossRef]
- Hu, S.; Bopp, P.A.; Österlund, L.; Broqvist, P.; Hermansson, K. Formic Acid on TiO2–x (110): Dissociation, Motion, and Vacancy Healing. J. Phys. Chem. C 2014, 118, 14876–14887. [Google Scholar] [CrossRef]
- Mattsson, A.; Hu, S.; Hermansson, K.; Österlund, L. Adsorption of Formic Acid on Rutile TiO2 (110) Revisited: An Infrared Reflection-Absorption Spectroscopy and Density Functional Theory Study. J. Chem. Phys. 2014, 140, 34705. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Selloni, A. Energetics and Diffusion of Intrinsic Surface and Subsurface Defects on Anatase TiO2(101). J. Chem. Phys. 2009, 131, 54703. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Noei, H.; Buchholz, M.; Muhler, M.; Wöll, C.; Wang, Y. Dissociation of Formic Acid on Anatase TiO2(101) Probed by Vibrational Spectroscopy. Catal. Today 2012, 182, 12–15. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Barone, V.; Casarin, M.; Forrer, D.; Pavone, M.; Sambi, M.; Vittadini, A. Role and Effective Treatment of Dispersive Forces in Materials: Polyethylene and Graphite Crystals as Test Cases. J. Comput. Chem. 2009, 30, 934–939. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Lichtenstein, A.I. First-Principles Calculations of the Electronic Structure and Spectra of Strongly Correlated Systems: The LDA + U Method. J. Phys. Condens. Matter 1997, 9, 767–808. [Google Scholar] [CrossRef] [Green Version]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band Theory and Mott Insulators: Hubbard U Instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Himmetoglu, B.; Floris, A.; de Gironcoli, S.; Cococcioni, M. Hubbard-Corrected DFT Energy Functionals: The LDA+U Description of Correlated Systems. Int. J. Quantum Chem. 2014, 114, 14–49. [Google Scholar] [CrossRef] [Green Version]
- Stausholm-Møller, J.; Kristoffersen, H.; Hinnemann, B.; Madsen, G.; Hammer, B. DFT+U Study of Defects in Bulk Rutile TiO2. J. Chem. Phys. 2010, 133, 144708. [Google Scholar] [CrossRef]
- Nolan, M.; Elliott, S.D.; Mulley, J.S.; Bennett, R.A.; Basham, M.; Mulheran, P. Electronic Structure of Point Defects in Controlled Self-Doping of the TiO2 Surface: Combined Photoemission Spectroscopy and Density Functional Theory Study. Phys. Rev. B 2008, 77, 235424. [Google Scholar] [CrossRef]
- Morita, K.; Shibuya, T.; Yasuoka, K. Stability of Excess Electrons Introduced by Ti Interstitial in Rutile TiO2(110) Surface. J. Phys. Chem. C 2017, 121, 1602–1607. [Google Scholar] [CrossRef]
- Lutfalla, S.; Shapovalov, V.; Bell, A.T. Calibration of the DFT/GGA+U Method for Determination of Reduction Energies for Transition and Rare Earth Metal Oxides of Ti, V, Mo, and Ce. J. Chem. Theory Comput. 2011, 7, 2218–2223. [Google Scholar] [CrossRef]
- Forrer, D.; Vittadini, A. 2D vs. 3D Titanium Dioxide: Role of Dispersion Interactions. Chem. Phys. Lett. 2011, 516, 72–75. [Google Scholar] [CrossRef]
- Bredow, T.; Giordano, L.; Cinquini, F.; Pacchioni, G. Electronic Properties of Rutile TiO2 Ultrathin Films: Odd-Even Oscillations with the Number of Layers. Phys. Rev. B 2004, 70, 35419. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forrer, D.; Vittadini, A. Effect of Formic Acid on the Outdiffusion of Ti Interstitials at TiO2 Surfaces: A DFT+U Investigation. Molecules 2022, 27, 6538. https://doi.org/10.3390/molecules27196538
Forrer D, Vittadini A. Effect of Formic Acid on the Outdiffusion of Ti Interstitials at TiO2 Surfaces: A DFT+U Investigation. Molecules. 2022; 27(19):6538. https://doi.org/10.3390/molecules27196538
Chicago/Turabian StyleForrer, Daniel, and Andrea Vittadini. 2022. "Effect of Formic Acid on the Outdiffusion of Ti Interstitials at TiO2 Surfaces: A DFT+U Investigation" Molecules 27, no. 19: 6538. https://doi.org/10.3390/molecules27196538
APA StyleForrer, D., & Vittadini, A. (2022). Effect of Formic Acid on the Outdiffusion of Ti Interstitials at TiO2 Surfaces: A DFT+U Investigation. Molecules, 27(19), 6538. https://doi.org/10.3390/molecules27196538