Redox Hyperactive MOF for Li+, Na+ and Mg2+ Storage
Abstract
:1. Introduction
2. Results and Discussion
2.1. Structure of Pristine MOF-S21
2.2. Metal Loading into MOF-S21
2.2.1. Lithiation of MOF-S21
2.2.2. Sodiation of MOF-S21
2.2.3. Magneziation of MOF-S21
2.3. Generalized Electrochemical Results
3. Models and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arroyo-de Dompablo, M.; Ponrouch, A.; Johansson, P.; Palacín, M. Achievements, Challenges, and Prospects of Calcium Batteries. Chem. Rev. 2020, 120, 6331–6357. [Google Scholar] [CrossRef]
- Elia, G.A.; Marquardt, K.; Hoeppner, K.; Fantini, S.; Lin, R.; Knipping, E.; Peters, W.; Drillet, J.-F.; Passerini, S.; Hahn, R. An Overview and Future Perspectives of Aluminum Batteries. Adv. Mater. 2016, 28, 7564–7579. [Google Scholar] [CrossRef] [PubMed]
- Qin, K.; Huang, J.; Holguin, K.; Luo, C. Recent advances in developing organic electrode materials for multivalent rechargeable batteries. Energy Environ. Sci. 2020, 13, 3950–3992. [Google Scholar] [CrossRef]
- Tian, Y.; Zeng, G.; Rutt, A.; Shi, T.; Kim, H.; Wang, J.; Koettgen, J.; Sun, Y.; Ouyang, B.; Chen, T.; et al. Promises and Challenges of Next-Generation “Beyond Li-ion” Batteries for Electric Vehicles and Grid Decarbonization. Chem. Rev. 2021, 121, 1623–1669. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.-Y.; Myung, S.-T.; Sun, Y.-K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muldoon, J.; Bucur, C.B.; Gregory, T. Quest for nonaqueous multivalent secondary batteries: Magnesium and beyond. Chem. Rev. 2014, 114, 11683–11720. [Google Scholar] [CrossRef] [PubMed]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research Development on Sodium-Ion Batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Fan, X.; Gao, T.; Sun, W.; Ma, Z.; Yang, C.; Han, F.; Xu, K.; Wang, C. High-Voltage Aqueous Magnesium Ion Batteries. ACS Cent. Sci. 2017, 3, 1121–1128. [Google Scholar] [CrossRef] [Green Version]
- Vanysek, P. Electrochemical series. In CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.-C.; Kitagawa, S. Metal–Organic Frameworks (MOFs). Chem. Soc. Rev. 2014, 43, 5415–5418. [Google Scholar] [CrossRef] [Green Version]
- Yaghi, O.M.; O’Keeffe, M.; Ockwig, N.W.; Chae, H.K.; Eddaoudi, M.; Kim, J. Reticular synthesis and the design of new materials. Nature 2003, 423, 705–714. [Google Scholar] [CrossRef]
- Lu, W.; Wei, Z.; Gu, Z.-Y.; Liu, T.-F.; Park, J.; Park, J.; Tian, J.; Zhang, M.; Zhang, Q.; Iii, T.G.; et al. Tuning the structure and function of metal–organic frameworks via linker design. Chem. Soc. Rev. 2014, 43, 5561–5593. [Google Scholar] [CrossRef]
- Odoh, S.O.; Cramer, C.; Truhlar, D.; Gagliardi, L. Quantum-Chemical Characterization of the Properties and Reactivities of Metal–Organic Frameworks. Chem. Rev. 2015, 115, 6051–6111. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Chen, J. Prospects of organic electrode materials for practical lithium batteries. Nat. Rev. Chem. 2020, 4, 127–142. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, Q.; Li, L.; Niu, Z.; Chen, J. Design Strategies toward Enhancing the Performance of Organic Electrode Materials in Metal-Ion Batteries. Chem 2018, 4, 2786–2813. [Google Scholar] [CrossRef] [Green Version]
- Esser, B.; Dolhem, F.; Becuwe, M.; Poizot, P.; Vlad, A.; Brandell, D. A perspective on organic electrode materials and technologies for next generation batteries. J. Power Sources 2021, 482, 228814. [Google Scholar] [CrossRef]
- Cui, X.; Dong, H.; Chen, S.; Wu, M.; Wang, Y. Progress and Perspective of Metal- and Covalent-Organic Frameworks and their Derivatives for Lithium-Ion Batteries. Batter. Supercaps 2020, 4, 72–97. [Google Scholar] [CrossRef]
- Wang, Z.; Tan, R.; Wang, H.; Yang, L.; Hu, J.; Chen, H.; Pan, F. A Metal-Organic-Framework-Based Electrolyte with Nanowetted Interfaces for High-Energy-Density Solid-State Lithium Battery. Adv. Mater. 2018, 30, 1704436. [Google Scholar] [CrossRef]
- Shrivastav, V.; Sundriyal, S.; Goel, P.; Kaur, H.; Tuteja, S.K.; Vikrant, K.; Kim, K.-H.; Tiwari, U.K.; Deep, A. Metal-organic frameworks (MOFs) and their composites as electrodes for lithium battery applications: Novel means for alternative energy storage. Coord. Chem. Rev. 2019, 393, 48–78. [Google Scholar] [CrossRef]
- Jaschin, P.W.; Gao, Y.; Li, Y.; Bo, S.-H. A materials perspective on magnesium-ion-based solid-state electrolytes. J. Mater. Chem. A 2020, 8, 2875–2897. [Google Scholar] [CrossRef]
- Calbo, J.; Golomb, M.J.; Walsh, A. Redox-active metal–organic frameworks for energy conversion and storage. J. Mater. Chem. A 2019, 7, 16571–16597. [Google Scholar] [CrossRef]
- Zhang, Z.; Yoshikawa, H.; Awaga, K. Monitoring the Solid-State Electrochemistry of Cu(2,7-AQDC) (AQDC = Anthraquinone Dicarboxylate) in a Lithium Battery: Coexistence of Metal and Ligand Redox Activities in a Metal–Organic Framework. J. Am. Chem. Soc. 2014, 136, 16112–16115. [Google Scholar] [CrossRef]
- Baumann, A.E.; Burns, D.A.; Liu, B.; Thoi, V.S. Metal-organic framework functionalization and design strategies for advanced electrochemical energy storage devices. Commun. Chem. 2019, 2, 86. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Wang, K.; Li, J.Z.; Zhang, Q. Nanostructured potassium–organic framework as an effective anode for potassium-ion batteries with a long cycle life. Nanoscale 2020, 12, 7870–7874. [Google Scholar] [CrossRef] [PubMed]
- Férey, G.; Millange, F.; Morcrette, M.; Serre, C.; Doublet, M.-L.; Grenèche, J.-M.; Tarascon, J.-M. Mixed-Valence Li/Fe-Based Metal–Organic Frameworks with Both Reversible Redox and Sorption Properties. Angew. Chem. Int. Ed. 2007, 46, 3259–3263. [Google Scholar] [CrossRef]
- Luo, D.; Lei, P.; Tian, G.; Huang, Y.; Ren, X.; Xiang, X. Insight into Electrochemical Properties and Reaction Mechanism of a Cobalt-Rich Prussian Blue Analogue Cathode in a NaSO3CF3 Electrolyte for Aqueous Sodium-Ion Batteries. J. Phys. Chem. C 2020, 124, 5958–5965. [Google Scholar] [CrossRef]
- Schon, T.B.; McAllister, B.T.; Li, P.-F.; Seferos, D.S. The rise of organic electrode materials for energy storage. Chem. Soc. Rev. 2016, 45, 6345–6404. [Google Scholar] [CrossRef] [Green Version]
- Huynh, M.; Anson, C.; Cavell, A.C.; Stahl, S.S.; Hammes-Schiffer, S. Quinone 1 e– and 2 e–/2 H+ Reduction Potentials: Identification and Analysis of Deviations from Systematic Scaling Relationships. J. Am. Chem. Soc. 2016, 138, 15903–15910. [Google Scholar] [CrossRef]
- Araujo, R.B.; Banerjee, A.; Panigrahi, P.; Yang, L.; Strømme, M.; Sjödin, M.; Araujo, C.M.; Ahuja, R. Designing strategies to tune reduction potential of organic molecules for sustainable high capacity battery application. J. Mater. Chem. A 2017, 5, 4430–4454. [Google Scholar] [CrossRef]
- Emanuelsson, R.; Sterby, M.; Strømme, M.; Sjödin, M. An All-Organic Proton Battery. J. Am. Chem. Soc. 2017, 139, 4828–4834. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.; Liu, L.; Shang, Z.; Li, Y.; Lu, Y.; Cheng, F.; Chen, J. The structure–electrochemical property relationship of quinone electrodes for lithium-ion batteries. Phys. Chem. Chem. Phys. 2018, 20, 13478–13484. [Google Scholar] [CrossRef] [PubMed]
- Oka, K.; Strietzel, C.; Emanuelsson, R.; Nishide, H.; Oyaizu, K.; Strømme, M.; Sjödin, M. Characterization of PEDOT-Quinone conducting redox polymers in water-in-salt electrolytes for safe and high-energy Li-ion batteries. Electrochem. Commun. 2019, 105, 106489. [Google Scholar] [CrossRef]
- Kim, K.C.; Liu, T.; Jung, K.H.; Lee, S.W.; Jang, S.S. Unveiled correlations between electron affinity and solvation in redox potential of quinone-based sodium-ion batteries. Energy Storage Mater. 2019, 19, 242–250. [Google Scholar] [CrossRef]
- Rasheev, H.G.; De Araújo, R.B.N.; Tadjer, A.; Johansson, P. Fundamental promise of anthraquinone functionalized graphene based next generation battery electrodes: A DFT study. J. Mater. Chem. A 2020, 8, 14152–14161. [Google Scholar] [CrossRef]
- Jung, K.H.; Jeong, G.; Go, C.Y.; Kim, K.C. Conjugacy of organic cathode materials for high-potential lithium-ion batteries: Carbonitriles versus quinones. Energy Storage Mater. 2019, 24, 237–246. [Google Scholar] [CrossRef]
- An, S.Y.; Schon, T.B.; Seferos, D.S. Stable, Dual Redox Unit Organic Electrodes. ACS Omega 2020, 5, 1134–1141. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Yi, X.; Liu, Z.X.; Shang, J.; Wang, D. Triphenylamine-Based Metal–Organic Frameworks as Cathode Materials in Lithium-Ion Batteries with Coexistence of Redox Active Sites, High Working Voltage, and High Rate Stability. ACS Appl. Mater. Interfaces 2016, 8, 14578–14585. [Google Scholar] [CrossRef]
- Gu, S.; Bai, Z.; Majumder, S.; Huang, B.; Chen, G. Conductive metal–organic framework with redox metal center as cathode for high rate performance lithium ion battery. J. Power Sources 2019, 429, 22–29. [Google Scholar] [CrossRef]
- Hmadeh, M.; Liu, Z.; Gándara, F.; Furukawa, H.; Wan, S.; Augustyn, V.; Chang, R.; Liao, L.; Zhou, F.; Perre, E.; et al. New Porous Crystals of Extended Metal-Catecholates. Chem. Mater. 2012, 24, 3511–3513. [Google Scholar] [CrossRef]
- Wu, Z.; Adekoya, D.; Huang, X.; Kiefel, M.J.; Xie, J.; Xu, W.; Zhang, Q.; Zhu, D.; Zhang, S. Highly Conductive Two-Dimensional Metal–Organic Frameworks for Resilient Lithium Storage with Superb Rate Capability. ACS Nano 2020, 14, 12016–12026. [Google Scholar] [CrossRef]
- Hameed, A.S.; Nagarathinam, M.; Schreyer, M.; Reddy, M.V.; Chowdari, B.V.R.; Vittal, J.J. A layered oxalatophosphate framework as a cathode material for Li-ion batteries. J. Mater. Chem. A 2013, 1, 5721–5726. [Google Scholar] [CrossRef]
- Wessells, C.D.; Peddada, S.V.; Huggins, R.A.; Cui, Y. Nickel Hexacyanoferrate Nanoparticle Electrodes for Aqueous Sodium and Potassium Ion Batteries. Nano Lett. 2011, 11, 5421–5425. [Google Scholar] [CrossRef]
- Li, X.; Cheng, F.; Zhang, S.; Chen, J. Shape-controlled synthesis and lithium-storage study of metal-organic frameworks Zn4O(1,3,5-benzenetribenzoate)2. J. Power Sources 2006, 160, 542–547. [Google Scholar] [CrossRef]
- Ogihara, N.; Yasuda, T.; Kishida, Y.; Ohsuna, T.; Miyamoto, K.; Ohba, N. Organic Dicarboxylate Negative Electrode Materials with Remarkably Small Strain for High-Voltage Bipolar Batteries. Angew. Chem. Int. Ed. 2014, 53, 11467–11472. [Google Scholar] [CrossRef] [PubMed]
- Hameed, S.; Petnikota, S.; Hassan, N.; Al-Qaradawi, S.; Karim, Z.; Reddy, M. Synthesis of Nickel Fumarate and Its Electrochemical Properties for Li-Ion Batteries. Electrochem 2021, 2, 439–451. [Google Scholar] [CrossRef]
- Lee, H.H.; Park, Y.; Kim, S.H.; Yeon, S.-H.; Kwak, S.K.; Lee, K.T.; Hong, S.Y. Mechanistic Studies of Transition Metal-Terephthalate Coordination Complexes upon Electrochemical Lithiation and Delithiation. Adv. Funct. Mater. 2015, 25, 4859–4866. [Google Scholar] [CrossRef]
- Lefebvre, J.; Chartrand, D.; Leznoff, D.B. Synthesis, structure and magnetic properties of 2-D and 3-D [cation]{M[Au(CN)2]3} (M=Ni,Co) coordination polymers. Polyhedron 2007, 26, 2189–2199. [Google Scholar] [CrossRef]
- Rasheev, H.; Stoyanova, R.; Tadjer, A. Rivalry at the Interface: Ion Desolvation and Electrolyte Degradation in Model Ethylene Carbonate Complexes of Li+, Na+, and Mg2+ with PF6– on the Li4Ti5O12 (111) Surface. ACS Omega 2021, 6, 29735–29745. [Google Scholar] [CrossRef]
- Tian, R.; Duan, H.; Guo, Y.; Li, H.; Liu, H. High-Coulombic-Efficiency Carbon/Li Clusters Composite Anode without Precycling or Prelithiation. Small 2018, 14, e1802226. [Google Scholar] [CrossRef] [PubMed]
- Bloi, L.M.; Hippauf, F.; Boenke, T.; Rauche, M.; Paasch, S.; Schutjajew, K.; Pampel, J.; Schwotzer, F.; Dörfler, S.; Althues, H.; et al. Mechanistic insights into the reversible lithium storage in an open porous carbon via metal cluster formation in all solid-state batteries. Carbon 2022, 188, 325–335. [Google Scholar] [CrossRef]
- Lyu, H.; Jafta, C.J.; Popovs, I.; Meyer, H.M.; Hachtel, J.A.; Huang, J.; Sumpter, B.G.; Dai, S.; Sun, X.-G. A dicyanobenzoquinone based cathode material for rechargeable lithium and sodium ion batteries. J. Mater. Chem. A 2019, 7, 17888–17895. [Google Scholar] [CrossRef]
- Bitenc, J.; Pavčnik, T.; Košir, U.; Pirnat, K. Quinone Based Materials as Renewable High Energy Density Cathode Materials for Rechargeable Magnesium Batteries. Materials 2020, 13, 506. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhang, C.; Xie, J.; Wang, K.; Li, J.; Zhang, Q. Ferrocene-based metal-organic framework as a promising cathode in lithium-ion battery. Chem. Eng. J. 2020, 404, 126463. [Google Scholar] [CrossRef]
- Cui, S.; Gao, M.; Li, G.; Gao, X. Insights into Li-Rich Mn-Based Cathode Materials with High Capacity: From Dimension to Lattice to Atom. Adv. Energy Mater. 2021, 2003885. [Google Scholar] [CrossRef]
- Do, J.; Kim, I.; Kim, H.; Jung, Y. Towards stable Na-rich layered transition metal oxides for high energy density sodium-ion batteries. Energy Storage Mater. 2020, 25, 62–69. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initiomolecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nosé, S. Constant Temperature Molecular Dynamics Methods. Prog. Theor. Phys. Suppl. 1991, 103, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. (Ser. I) 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Aydinol, M.; Kohan, A.F.; Ceder, G.; Cho, K.; Joannopoulos, J. Ab initiostudy of lithium intercalation in metal oxides and metal dichalcogenides. Phys. Rev. B 1997, 56, 1354–1365. [Google Scholar] [CrossRef] [Green Version]
- Araujo, R.B.; Banerjee, A.; Ahuja, R. Divulging the Hidden Capacity and Sodiation Kinetics of NaxC6Cl4O2: A High Voltage Organic Cathode for Sodium Rechargeable Batteries. J. Phys. Chem. C 2017, 121, 14027–14036. [Google Scholar] [CrossRef]
- Lambert, F.; Danten, Y.; Gatti, C.; Frayret, C. A tool for deciphering the redox potential ranking of organic compounds: A case study of biomass-extracted quinones for sustainable energy. Phys. Chem. Chem. Phys. 2020, 22, 20212–20226. [Google Scholar] [CrossRef] [PubMed]












| n(Li) | qave(Li) | q(Ni) | Volume of Unit Cell, ų | Coord. # of Ni R(CN…Ni) < 2.3 Å | # Li-Li Bonds R(Li-Li) < 2.67 Å |
|---|---|---|---|---|---|
| 0 | – | 1.25 | 1024.8 | 6 | |
| 2 | 0.88 | 1.21 | 795.3 | 6 | 0 |
| 4 | 0.87 | 1.21 | 753.9 | 6 | 0 |
| 8 | 0.87 | 0.75 | 763.9 | 4 | 5 |
| 18 | 0.86 | 0.32 | 770.7 | 3 | 7 |
| 24 | 0.84 | 0.24 | 794.1 | 2 | 10 |
| 26 | 0.75 | 0.05 | 872.9 | 2 | 13 |
| Metal | a, Å | b, Å | c, Å | α, ° | β, ° | γ, ° |
|---|---|---|---|---|---|---|
| 0 | 11.67 | 11.67 | 11.67 | 56.16 | 56.16 | 56.16 |
| 24 Li | 10.79 | 11.77 | 12.08 | 50.27 | 43.85 | 54.06 |
| 16 Na | 9.19 | 11.15 | 10.64 | 91.77 | 68.65 | 108.54 |
| 6 Mg | 10.08 | 10.83 | 11.15 | 61.92 | 61.15 | 65.21 |
| n(Na) | qavr(Na) | Volume of Unit Cell, ų | q(Ni) | Coord. # of Ni R(CN…Ni) < 2.3 Å | # Na-Na Bonds R(Na-Na) < 3.08 Å |
|---|---|---|---|---|---|
| 0 | – | 1024.8 | 1.25 | 6 | |
| 4 | 0.88 | 869.0 | 1.18 | 6 | 0 |
| 6 | 0.88 | 851.3 | 0.94 | 4 | 0 |
| 8 | 0.88 | 946.3 | 0.61 | 4 | 0 |
| 10 | 0.88 | 963.3 | 0.51 | 4 | 0 |
| 12 | 0.86 | 985.4 | 0.46 | 4 | 1 |
| 14 | 0.86 | 993.3 | 0.44 | 4 | 1 |
| 16 | 0.76 | 959.4 | 0.43 | 4 | 1 |
| 18 | 0.69 | 974.0 | 0.40 | 4 | 1 |
| n(Mg) | qave(Mg) | Volume of Unit Cell, ų | q(Ni) | Coord. # of Ni R(CN…Ni) < 2.3 Å | # Mg-Mg R(Mg-Mg) < 2.85 Å |
|---|---|---|---|---|---|
| 0 | - | 1024.8 | 1.25 | 6 | |
| 2 | 1.77 | 944.4 | 1.24 | 6 | 0 |
| 3 | 1.71 | 802.8 | 1.24 | 6 | 0 |
| 4 | 1.71 | 770.6 | 0.82 | 5 | 0 |
| 5 | 1.69 | 750.1 | 0.79 | 4 | 0 |
| 6 | 1.47 | 910.9 | 0.74 | 4 | 0 |
| 8 | 1.30 | 950.6 | 0.14 | 2 | 0 |
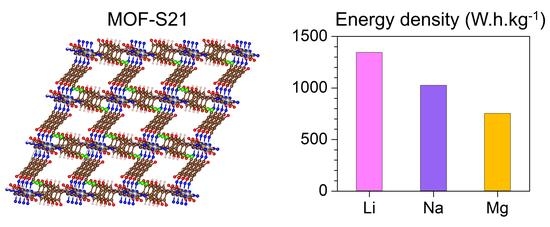
| Charge Carrier | Maximum Capacity | Gravimetric Energy Density |
|---|---|---|
| 24 Li | 1065 | 1343 |
| 16 Na | 710 | 1025 |
| 6 Mg | 533 | 753 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasheev, H.; Seremak, A.; Stoyanova, R.; Tadjer, A. Redox Hyperactive MOF for Li+, Na+ and Mg2+ Storage. Molecules 2022, 27, 586. https://doi.org/10.3390/molecules27030586
Rasheev H, Seremak A, Stoyanova R, Tadjer A. Redox Hyperactive MOF for Li+, Na+ and Mg2+ Storage. Molecules. 2022; 27(3):586. https://doi.org/10.3390/molecules27030586
Chicago/Turabian StyleRasheev, Hristo, Agnieszka Seremak, Radostina Stoyanova, and Alia Tadjer. 2022. "Redox Hyperactive MOF for Li+, Na+ and Mg2+ Storage" Molecules 27, no. 3: 586. https://doi.org/10.3390/molecules27030586
APA StyleRasheev, H., Seremak, A., Stoyanova, R., & Tadjer, A. (2022). Redox Hyperactive MOF for Li+, Na+ and Mg2+ Storage. Molecules, 27(3), 586. https://doi.org/10.3390/molecules27030586