Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS
Abstract
:1. Introduction
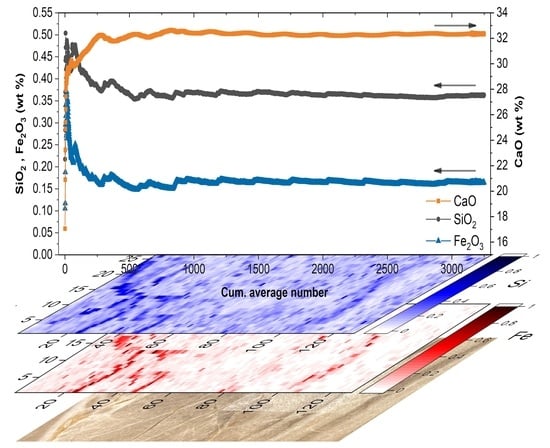
2. Results and Discussion
3. Materials and Methods
3.1. Setup
3.2. Samples
3.3. Analytical Methods
3.3.1. PLS Regression Method
3.3.2. MLP Regression Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Dowling, A.; O’Dwyer, J.; Adley, C.C. Lime in the limelight. J. Clean. Prod. 2015, 92, 13–22. [Google Scholar] [CrossRef]
- 2019–020 Activity Report of The European Lime Association. Available online: https://www.eula.eu/2019-2020-eula-activity-report/ (accessed on 10 February 2022).
- Bell, F.G. Lime stabilization of clay minerals and soils. Eng. Geol. 1996, 42, 223–237. [Google Scholar] [CrossRef]
- Manocha, S.; Ponchon, F. Management of Lime in Steel. Metals 2018, 8, 686. [Google Scholar] [CrossRef] [Green Version]
- Vola, G.; Sarandrea, L.; Della Porta, G.; Cavallo, A.; Jadoul, F.; Cruciani, G. The influence of petrography, mineralogy and chemistry on burnability and reactivity of quicklime produced in Twin Shaft Regenerative (TSR) kilns from Neoarchean limestone (Transvaal Supergroup, South Africa). Miner. Pet. 2018, 112, 555–576. [Google Scholar] [CrossRef]
- Vola, G.; Bresciani, P.; Rodeghero, E.; Sarandrea, L.; Cruciani, G. Impact of rock fabric, thermal behavior, and carbonate decomposition kinetics on quicklime industrial production and slaking reactivity. J. Therm. Anal. Calorim. 2019, 136, 967–993. [Google Scholar] [CrossRef]
- Singh, J.P.; Thakur, S.N. Laser-Induced Breakdown Spectroscopy, 2nd ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Grant, K.J.; Paul, G.L.; O’Neill, J.A. Time-resolved laser-induced breakdown spectroscopy of iron ore. Appl. Spectrosc. 1990, 44, 1711–1714. [Google Scholar] [CrossRef]
- Vadillo, J.M.; Laserna, J.J. Laser-induced breakdown spectroscopy of silicate, vanadate and sulfide rocks. Talanta 1996, 43, 1149–1154. [Google Scholar] [CrossRef]
- Sun, Q.; Tran, M.; Smith, B.W.; Winefordner, J.D. Determination of Mn and Si in iron ore by laser-induced plasma spectroscopy. Anal. Chim. Acta 2000, 413, 187–195. [Google Scholar] [CrossRef]
- Kaski, S.; Häkkänen, H.; Korppi-Tommola, J. Sulfide mineral identification using laser-induced plasma spectroscopy. Miner. Eng. 2003, 16, 1239–1243. [Google Scholar] [CrossRef]
- McMillan, N.J.; Harmon, R.S.; De Lucia, F.C.; Miziolek, A.M. Laser-induced breakdown spectroscopy analysis of minerals: Carbonates and silicates. Spectrochim. Acta Part B 2007, 62, 1528–1536. [Google Scholar] [CrossRef]
- Alvey, D.C.; Morton, K.; Harmon, R.S.; Gottfried, J.L.; Remus, J.J.; Collins, L.M.; Wise, M.A. Laser-induced breakdown spectroscopy-based geochemical fingerprinting for the rapid analysis and discrimination of minerals: The example of garnet. Appl. Opt. 2010, 49, C168–C180. [Google Scholar] [CrossRef] [Green Version]
- Bolger, J.A. Semi-Quantitative Laser-Induced Breakdown Spectroscopy for Analysis of Mineral Drill Core. Appl. Spectrosc. 2000, 54, 181–189. [Google Scholar] [CrossRef]
- Rosenwasse, S.; Asimellisa, G.; Bromleya, B.; Hazletta, R.; Martinb, J.; Pearceb, T.; Ziglera, A. Development of a method for automated quantitative analysis of ores using LIBS. Spectrochim. Acta Part B 2001, 56, 707–714. [Google Scholar] [CrossRef]
- Death, D.L.; Cunningham, A.P.; Pollard, L.J. Multi-element and mineralogical analysis of mineral ores using laser induced breakdown spectroscopy and chemometric analysis. Spectrochim. Acta Part B 2009, 64, 1048–1058. [Google Scholar] [CrossRef]
- Gaft, M.; Sapir-Sofer, I.; Modiano, H.; Stana, R. Laser induced breakdown spectroscopy for bulk minerals online analyses. Appl. Spectrosc. 2007, 62, 1496–1503. [Google Scholar] [CrossRef]
- Gaft, M.; Nagli, L.; Fasaki, I.; Kompitsas, M.; Wilsch, G. Laser-induced breakdown spectroscopy for on-line sulfur analyses of minerals in ambient conditions. Spectrochim. Acta Part B 2009, 64, 1098–1104. [Google Scholar] [CrossRef]
- Barrette, L.; Turmel, S. On-line iron-ore slurry monitoring for real-time process control of pellet making processes using laser-induced breakdown spectroscopy: Graphitic vs. total carbon detection. Spectrochim. Acta Part B 2001, 56, 715–723. [Google Scholar] [CrossRef]
- Pedarnig, J.D.; Trautner, S.; Grünberger, S.; Giannakaris, N.; Eschlböck-Fuchs, S.; Hofstadler, J. Review of Element Analysis of Industrial Materials by In-Line Laser—Induced Breakdown Spectroscopy (LIBS). Appl. Sci. 2021, 11, 9274. [Google Scholar] [CrossRef]
- Harmon, S.; Senesi, G.S. Laser-Induced Breakdown Spectroscopy—A geochemical tool for the 21st century. Appl. Geochem. 2021, 128, 104929. [Google Scholar] [CrossRef]
- Senesi, G.S.; Harmon, R.S.; Hark, R.R. Field-portable and handheld laser-induced breakdown spectroscopy: Historical review, current status and future prospects. Spectrochim. Acta Part B 2021, 175, 106013. [Google Scholar] [CrossRef]
- Osticioli, I.; Agresti, J.; Fornacelli, C.; Memmi, I.T.; Siano, S. Potential role of LIPS elemental depth profiling in authentication studies of unglazed earthenware artifacts. J. Anal. At. Spectrom. 2012, 27, 827–833. [Google Scholar] [CrossRef]
- Agresti, J.; Osticioli, I.; Guidotti, M.C.; Kardjilov, N.; Siano, S. Non-invasive archaeometallurgical approach to the investigations of bronze figurines using neutron, laser, and X-ray techniques. Microchem. J. 2016, 124, 765–774. [Google Scholar] [CrossRef]
- Dambruoso, P.; Siano, S.; Torreggiani, A.; Russo, O.; Marzocchi, S.; Dal Santo, V. The Italian National Research Council Operations within the EIT Raw Materials Framework. In Rare Metal Technology; Azimi, G., Ouchi, T., Forsberg, K., Kim, H., Alam, S., Baba, A.A., Neelameggham, N.R., Eds.; The Minerals, Metals & Materials Series; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Tucker, J.M.; Dyar, M.D.; Schaefer, M.W.; Clegg, S.M.; Wiens, R.C. Optimization of laser-induced breakdown spectroscopy for rapid geochemical analysis. Chem. Geol. 2010, 277, 137–148. [Google Scholar] [CrossRef]
- Motto-Ros, V.; Koujelev, A.; Osinski, G.; Dudelzak, A. Quantitative multi-elemental laser-induced breakdown spectroscopy using artificial neural networks. J. Eur. Opt. Soc. Rapid Publ. 2008, 3, 08011. [Google Scholar] [CrossRef]
- El Haddad, J.; Villot-Kadri, M.; Ismael, A.; Gallou, G.; Michel, K.; Bruyère, D.; Laperche, V.; Canioni, L.; Bousquet, B. Artificial neural network for on-site quantitative analysis of soils using laser induced breakdown spectroscopy. Spectrochim. Acta Part B 2013, 78–79, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Indelicato, C.; Osticioli, I.; Agresti, J.; Ciofini, D.; Mencaglia, A.A.; Perotti, M.; Viti, C.; Moreschi, R.; Siano, S. Exploring grain sizing of sedimentary calcareous rocks using Raman spectroscopy. Eur. Phys. J. Plus 2022, in press. [Google Scholar] [CrossRef]
- Sirven, J.-B.; Bousquet, B.; Canioni, L.; Sarger, L. Laser-Induced Breakdown Spectroscopy of Composite Samples: Comparison of Advanced Chemometrics Methods. Anal. Chem. 2006, 78, 1462–1469. [Google Scholar] [CrossRef]
- Pagnotta, S.; Lezzerini, M.; Campanella, B.; Legnaioli, S.; Poggialini, F.; Palleschi, V. A new approach to non-linear multivariate calibration in laser-induced breakdown spectroscopy analysis of silicate rocks. Spectrochim. Acta Part B 2020, 166, 105804. [Google Scholar] [CrossRef]
- Anderson, R.B.; Morris, R.V.; Clegg, S.M.; Bell, J.F.; Wiens, R.C.; Humphries, S.D.; Mertzman, S.A.; Graff, T.G.; McInroy, R. The influence of multivariate analysis methods and target grain size on the accuracy of remote quantitative chemical analysis of rocks using laser induced breakdown spectroscopy. Icarus 2011, 215, 608–627. [Google Scholar] [CrossRef]
- McCanta, M.C.; Dyar, M.D.; Dobosh, P.A. Extracting Bulk Rock Properties from Microscale Measurements: Subsampling and Analytical Guidelines. GSA Today 2017, 27, 4–9. [Google Scholar] [CrossRef]
- McCanta, M.C.; Dobosh, P.A.; Dyar, M.D.; Newsom, H.E. Testing the veracity of LIBS analyses on Mars using the LIBSSIM program. Planet. Space Sci. 2013, 81, 48–54. [Google Scholar] [CrossRef]
- Dyar, M.D.; Ytsma, C.R. Effect of data set size on geochemical quantification accuracy with laser-induced breakdown spec-troscopy. Spectrochim. Acta Part B 2021, 177, 106073. [Google Scholar] [CrossRef]
- Pagnotta, S.; Lezzerini, M.; Campanella, B.; Gallello, G.; Grifoni, E.; Legnaioli, S.; Lorenzetti, G.; Poggialini, F.; Raneri, S.; Safi, A.; et al. Fast quantitative elemental mapping of highly inhomogeneous materials by micro-Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta Part B 2018, 146, 9–15. [Google Scholar] [CrossRef] [Green Version]
- Chirinos, J.R.; Oropeza, D.D.; Gonzalez, J.J.; Hou, H.; Morey, M.; Zorba, V.; Russo, R.E. Simultaneous 3-dimensional elemental imaging with LIBS and LA-ICP-MS. J. Anal. At. Spectrom. 2014, 29, 1292–1298. [Google Scholar] [CrossRef]
- Lefebvre, C.; Catalá-Espí, A.; Sobron, P.; Koujelev, A.; Léveillé, R. Depth-resolved chemical mapping of rock coatings using Laser-Induced Breakdown Spectroscopy: Implications for geochemical investigations on Mars. Planet. Space Sci. 2016, 126, 24–33. [Google Scholar] [CrossRef]
- Senesi, G.S.; Campanella, B.; Grifoni, E.; Legnaioli, S.; Lorenzetti, G.; Pagnotta, S.; Poggialini, F.; Palleschi, V.; De Pascale, O. Elemental and mineralogical imaging of a weathered limestone rock by double-pulse micro-Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta Part B 2018, 143, 91–97. [Google Scholar] [CrossRef]
- Gervais, F.; Rifai, K.; Plamondon, P.; Özcan, L.; Doucet, F.; Vidal, F. Compositional tomography of a gold-bearing sample by Laser induced breakdown spectroscopy. Terra Nova 2019, 31, 479–484. [Google Scholar] [CrossRef]
- Labbé, N.; Swamidoss, I.M.; André, N.; Martin, M.Z.; Young, T.M.; Rials, T.G. Extraction of information from laser-induced breakdown spectroscopy spectral data by multivariate analysis. Appl. Opt. 2008, 47, G158–G165. [Google Scholar] [CrossRef]
- Boucher, T.F.; Ozanne, M.V.; Carmosino, M.L.; Dyar, M.D.; Mahadevan, S.; Breves, E.A.; Lepore, K.H.; Clegg, S.M. A study of machine learning regression methods for major elemental analysis of rocks using laser-induced breakdown spectroscopy. Spectrochim. Acta Part B 2015, 107, 1–10. [Google Scholar] [CrossRef]
- Li, L.-N.; Liu, X.-F.; Yang, F.; Xu, W.-M.; Wang, J.-Y.; Shu, R. A review of artificial neural network based chemometrics applied in laser-induced breakdown spectroscopy analysis. Spectrochim. Acta Part. B 2021, 180, 106183. [Google Scholar] [CrossRef]
- Ryan, C.G.; Clayton, E.; Griffin, W.L.; Sie, S.H.; Cousens, D.R. SNIP, a statistics-sensitive background treatment for the quantitative analysis of PIXE spectra in geoscience applications. Nucl. Instrum. Methods Phys. Res. Sect. B 1988, 34, 396–402. [Google Scholar] [CrossRef]
- Guezenoc, J.; Gallet-Budynek, A.; Bousquet, B. Critical review and advices on spectral-based normalization methods for LIBS quantitative analysis. Spectrochim. Acta Part B 2019, 160, 105688. [Google Scholar] [CrossRef]
- El Haddad, J.; Canioni, L.; Bousquet, B. Good practices in LIBS analysis: Review and advices. Spectrochim. Acta Part B 2014, 101, 171–182. [Google Scholar] [CrossRef] [Green Version]
- Cacciari, I.; Corradi, G. Common plastics THz classification via artificial neural networks: A discussion on a class of time domain features. Opt. Mater. 2021, 117, 111134. [Google Scholar] [CrossRef]
- Cacciari, I.; Pocobelli, G.F. Machine learning: A novel tool for archaeology. In Handbook of Cultural Heritage Analysis; D’Amico, S., Venuti, V., Eds.; Springer Nature: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]








| Oxide | Bands Exclusion + Avg. | Norm. + Avg. | Bands Exclusion + Norm. + Avg. | PLS Factors |
|---|---|---|---|---|
| CaO | +29% | −37% | −20% | 7 |
| MgO | +44% | −64% | −43% | 8 |
| SiO2 | −22% | −36% | −57% | 18 |
| Al2O3 | −21% | −55% | −73% | 17 |
| Fe2O3 | −22% | −46% | −56% | 13 |
| Oxide | Calibration Range (28 Samples) (wt.%) | Validation Range (5 Samples) (wt.%) | RMSECV (wt.%) | RMSEP (wt.%) | PLS Factors |
|---|---|---|---|---|---|
| CaO | 30.61–55.74 | 31.01–55.34 | 0.57 | 0.91 | 7 |
| MgO | 0.26–21.79 | 0.43–21.77 | 0.44 | 0.82 | 8 |
| SiO2 | 0–6.95 | 0.003–0.14 | 0.085 | 0.057 | 18 |
| Al2O3 | 0–2.24 | 0.009–0.076 | 0.033 | 0.038 | 17 |
| Fe2O3 | 0.002–0.68 | 0.007–0.045 | 0.019 | 0.015 | 13 |
| CaO | MgO | SiO2 | Fe2O3 | Al2O3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PLS | ANN | PLS | ANN | PLS | ANN | PLS | ANN | PLS | ANN | |
| P29 | 30.72 (0.27) | 31.05 (0.48) | 21.63 (0.37) | 21.64 (0.17) | 0.17 (0.03) | 0.10 (0.01) | 0.047 (0.016) | 0.040 (0.008) | 0.061 (0.021) | 0.070 (0.007) |
| P30 | 47.89 (0.24) | 48.96 (0.82) | 6.86 (0.22) | 5.25 (0.86) | 0.024 (0.029) | 0.084 (0.012) | 0.052 (0.012) | 0.047 (0.009) | 0.01 (0.01) | 0.052 (0.034) |
| P31 | 55.65 (0.09) | 55.36 (0.32) | 0.31 (0.12) | 0.42 (0.25) | 0.005 (0.021) | 0.004 (0.002) | 0.006 (0.007) | 0.006 (0.001) | 0.018 (0.006) | 0.012 (0.002) |
| P32 | 54.89 (0.10) | 54.37 (0.15) | 0.85 (0.11) | 0.61 (0.24) | 0.10 (0.01) | 0.030 (0.018) | 0.019 (0.011) | 0.008 (0.001) | 0.058 (0.015) | 0.023 (0.012) |
| P33 | 29.91 (0.27) | 31.83 (0.40) | 21.97 (0.30) | 20.44 (0.34) | 0.14 (0.02) | 0.177 (0.037) | 0.033 (0.014) | 0.022 (0.005) | 0.081 (0.024) | 0.071 (0.007) |
| Calibration Samples | CaO | MgO | SiO2 | Fe2O3 | Al2O3 |
| P1 | 30.610 | 21.570 | 0.070 | 0.050 | 0.030 |
| P2 | 31.481 | 21.744 | 0.059 | 0.037 | 0.053 |
| P3 | 31.100 | 21.787 | 0.000 | 0.018 | 0.009 |
| P4 | 46.170 | 8.010 | 0.040 | 0.030 | 0.040 |
| P5 | 50.640 | 1.150 | 4.410 | 0.460 | 1.550 |
| P6 | 30.750 | 21.380 | 0.050 | 0.050 | 0.040 |
| P7 | 47.960 | 1.470 | 6.950 | 0.680 | 2.240 |
| P8 | 52.760 | 0.860 | 2.580 | 0.220 | 0.710 |
| P9 | 54.930 | 0.580 | 0.290 | 0.020 | 0.130 |
| P10 | 31.860 | 20.330 | 0.060 | 0.070 | 0.040 |
| P11 | 43.540 | 10.170 | 0.370 | 0.060 | 0.070 |
| P12 | 50.730 | 4.120 | 0.250 | 0.030 | 0.110 |
| P13 | 33.380 | 18.220 | 1.180 | 0.160 | 0.420 |
| P14 | 30.900 | 21.047 | 0.205 | 0.045 | 0.127 |
| P15 | 31.430 | 21.322 | 0.167 | 0.037 | 0.095 |
| P16 | 46.470 | 7.977 | 0.148 | 0.049 | 0.093 |
| P17 | 38.637 | 14.548 | 0.347 | 0.075 | 0.176 |
| P18 | 53.380 | 1.333 | 0.193 | 0.048 | 0.110 |
| P19 | 55.220 | 0.420 | 0.119 | 0.024 | 0.060 |
| P20 | 55.530 | 0.301 | 0.025 | 0.016 | 0.022 |
| P21 | 55.600 | 0.192 | 0.100 | 0.032 | 0.072 |
| P22 | 55.750 | 0.590 | 0.082 | 0.016 | 0.043 |
| P23 | 31.920 | 20.575 | 0.173 | 0.031 | 0.111 |
| P24 | 32.820 | 20.505 | 0.034 | 0.007 | 0.030 |
| P25 | 54.730 | 0.822 | 0.193 | 0.045 | 0.081 |
| P26 | 51.220 | 0.717 | 3.366 | 0.442 | 1.112 |
| P27 | 55.130 | 0.390 | 0.033 | 0.009 | 0.013 |
| P28 | 55.350 | 0.258 | 0.004 | 0.002 | 0.000 |
| Validation Samples | CaO | MgO | SiO2 | Fe2O3 | Al2O3 |
| P29 | 31.013 | 21.766 | 0.114 | 0.035 | 0.076 |
| P30 | 48.574 | 5.602 | 0.094 | 0.045 | 0.060 |
| P31 | 55.339 | 0.432 | 0.003 | 0.007 | 0.010 |
| P32 | 54.155 | 0.580 | 0.031 | 0.009 | 0.019 |
| P33 | 31.568 | 20.787 | 0.140 | 0.027 | 0.074 |
| Wavelength (nm) | Element | Wavelength (nm) | Element |
|---|---|---|---|
| 251.61 | Si | 309.3 | Al |
| 259.94 | Fe | 393.37 | Ca |
| 274.91 | Fe | 396.85 | Ca |
| 279.55 | Mg | 422.67 | Ca |
| 285.21 | Mg | 438.35 | Fe |
| 288.16 | Si | 517.27 | Mg |
| 308.21 | Al |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agresti, J.; Indelicato, C.; Perotti, M.; Moreschi, R.; Osticioli, I.; Cacciari, I.; Mencaglia, A.A.; Siano, S. Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS. Molecules 2022, 27, 1813. https://doi.org/10.3390/molecules27061813
Agresti J, Indelicato C, Perotti M, Moreschi R, Osticioli I, Cacciari I, Mencaglia AA, Siano S. Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS. Molecules. 2022; 27(6):1813. https://doi.org/10.3390/molecules27061813
Chicago/Turabian StyleAgresti, Juri, Carlo Indelicato, Matteo Perotti, Roberto Moreschi, Iacopo Osticioli, Ilaria Cacciari, Andrea Azelio Mencaglia, and Salvatore Siano. 2022. "Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS" Molecules 27, no. 6: 1813. https://doi.org/10.3390/molecules27061813
APA StyleAgresti, J., Indelicato, C., Perotti, M., Moreschi, R., Osticioli, I., Cacciari, I., Mencaglia, A. A., & Siano, S. (2022). Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS. Molecules, 27(6), 1813. https://doi.org/10.3390/molecules27061813