New Generation of MOF-Monoliths Based on Metal Foams
Abstract
:1. Introduction
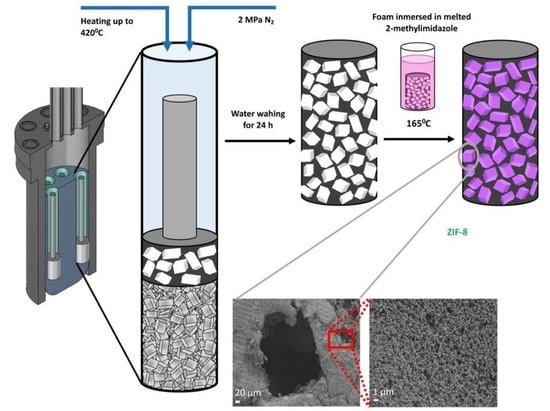
2. Experimental
3. Results
Manufacture and Characterization of Foam
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Rogge, S.M.J.; Bavykina, A.; Hajek, J.; Garcia, H.; Olivos-Suarez, A.I.; Sepúlveda-Escribano, A.; Vimont, A.; Clet, G.; Bazin, P.; Kapteijn, F.; et al. Metal-organic and covalent organic frameworks as single-site catalysts. Chem. Soc. Rev. 2017, 46, 3134–3184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rivero-Crespo, M.A.; Mon, M.; Ferrando-Soria, J.; Lopes, C.W.; Boronat, M.; Leyva-Pérez, A.; Corma, A.; Hernández-Garrido, J.C.; López-Haro, M.; Calvino, J.J.; et al. Confined Pt11+ Water Clusters in a MOF Catalyze the Low-Temperature Water–Gas Shift Reaction with both CO2 Oxygen Atoms Coming from Water. Angew. Chem.—Int. Ed. 2018, 57, 17094–17099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Casco, M.E.; Cheng, Y.Q.; Daemen, L.L.; Fairen-Jimenez, D.; Ramos-Fernández, E.V.; Ramirez-Cuesta, A.J.; Silvestre-Albero, J. Gate-opening effect in ZIF-8: The first experimental proof using inelastic neutron scattering. Chem. Commun. 2016, 52, 3639–3642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramos-Fernandez, E.V.; Grau-Atienza, A.; Farrusseng, D.; Aguado, S. A water-based room temperature synthesis of ZIF-93 for CO2 adsorption. J. Mater. Chem. A 2018, 6, 5598–5602. [Google Scholar] [CrossRef] [Green Version]
- Grancha, T.; Mon, M.; Ferrando-Soria, J.; Gascon, J.; Seoane, B.; Ramos-Fernandez, E.V.; Armentano, D.; Pardo, E. Tuning the selectivity of light hydrocarbons in natural gas in a family of isoreticular MOFs. J. Mater. Chem. A 2017, 5, 11032–11039. [Google Scholar] [CrossRef] [Green Version]
- Casco, M.E.; Fernández-Catalá, J.; Cheng, Y.; Daemen, L.; Ramirez-Cuesta, A.J.; Cuadrado-Collados, C.; Silvestre-Albero, J.; Ramos-Fernandez, E.V. Understanding ZIF-8 Performance upon Gas Adsorption by Means of Inelastic Neutron Scattering. ChemistrySelect 2017, 2, 2750–2753. [Google Scholar] [CrossRef]
- Wang, C.; Liu, D.; Lin, W. Metal-organic frameworks as a tunable platform for designing functional molecular materials. J. Am. Chem. Soc. 2013, 135, 13222–13234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, B.; He, Y.; Han, L.; Singh, V.; Xu, X.; Guo, T.; Meng, F.; Xu, X.; York, P.; Liu, Z.; et al. Microwave-Assisted Rapid Synthesis of γ-Cyclodextrin Metal–Organic Frameworks for Size Control and Efficient Drug Loading. Cryst. Growth Des. 2017, 17, 1654–1660. [Google Scholar] [CrossRef]
- Chu, Y.; Hou, J.; Boyer, C.; Richardson, J.J.; Liang, K.; Xu, J. Biomimetic synthesis of coordination network materials: Recent advances in MOFs and MPNs. Appl. Mater. Today 2018, 10, 93–105. [Google Scholar] [CrossRef]
- Lee, Y.R.; Jang, M.S.; Cho, H.Y.; Kwon, H.J.; Kim, S.; Ahn, W.S. ZIF-8: A comparison of synthesis methods. Chem. Eng. J. 2015, 271, 276–280. [Google Scholar] [CrossRef]
- Avci, C.; Ariñez-Soriano, J.; Carné-Sánchez, A.; Guillerm, V.; Carbonell, C.; Imaz, I.; Maspoch, D. Post-Synthetic Anisotropic Wet-Chemical Etching of Colloidal Sodalite ZIF Crystals. Angew. Chem. Int. Ed. 2015, 54, 14417–14421. [Google Scholar] [CrossRef] [PubMed]
- Pang, S.H.; Han, C.; Sholl, D.S.; Jones, C.W.; Lively, R.P. Facet-Specific Stability of ZIF-8 in the Presence of Acid Gases Dissolved in Aqueous Solutions. Chem. Mater. 2016, 28, 6960–6967. [Google Scholar] [CrossRef]
- Tanaka, S.; Fujita, K.; Miyake, Y.; Miyamoto, M.; Hasegawa, Y.; Makino, T.; Van der Perre, S.; Cousin Saint Remi, J.; Van Assche, T.; Baron, G.V.; et al. Adsorption and Diffusion Phenomena in Crystal Size Engineered ZIF-8 MOF. J. Phys. Chem. C 2015, 119, 28430–28439. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Duan, B.; Luo, Q.; Gu, Z.; Liu, J.; Duan, C. Facet-dependent catalytic activity of ZIF-8 nanocubes and rhombic dodecahedra based on tracing substrate diffusion in pores by SERS: A case study for surface catalysis of MOFs. Catal. Sci. Technol. 2016, 6, 1616–1620. [Google Scholar] [CrossRef]
- Hu, L.; Chen, L.; Fang, Y.; Wang, A.; Chen, C.; Yan, Z. Facile synthesis of zeolitic imidazolate framework-8 (ZIF-8) by forming imidazole-based deep eutectic solvent. Microporous Mesoporous Mater. 2018, 268, 207–215. [Google Scholar] [CrossRef]
- Qian, J.; Sun, F.; Qin, L. Hydrothermal synthesis of zeolitic imidazolate framework-67 (ZIF-67) nanocrystals. Mater. Lett. 2012, 82, 220–223. [Google Scholar] [CrossRef]
- Chen, M.; Gan, N.; Zhou, Y.; Li, T.; Xu, Q.; Cao, Y.; Chen, Y. A novel aptamer- metal ions- nanoscale MOF based electrochemical biocodes for multiple antibiotics detection and signal amplification. Sens. Actuators B Chem. 2017, 242, 1201–1209. [Google Scholar] [CrossRef]
- Narciso, J.; Ramos-Fernandez, E.V.; Delgado-Marín, J.J.; Affolter, C.W.; Olsbye, U.; Redekop, E.A. New route for the synthesis of Co-MOF from metal substrates. Microporous Mesoporous Mater. 2021, 324, 111310. [Google Scholar] [CrossRef]
- Juan-Alcañiz, J.; Gielisse, R.; Lago, A.B.; Ramos-Fernandez, E.V.; Serra-Crespo, P.; Devic, T.; Guillou, N.; Serre, C.; Kapteijn, F.; Gascon, J. Towards acid MOFs—Catalytic performance of sulfonic acid functionalized architectures. Catal. Sci. Technol. 2013, 3, 2311. [Google Scholar] [CrossRef] [Green Version]
- Nouar, F.; Breeze, M.I.; Campo, B.C.; Vimont, A.; Clet, G.; Daturi, M.; Devic, T.; Walton, R.I.; Serre, C. Tuning the properties of the UiO-66 metal organic framework by Ce substitution. Chem. Commun. 2015, 51, 14458–14461. [Google Scholar] [CrossRef]
- Cao, S.-L.; Yue, D.-M.; Li, X.-H.; Smith, T.J.; Li, N.; Zong, M.-H.; Wu, H.; Ma, Y.-Z.; Lou, W.-Y. Novel Nano-/Micro-Biocatalyst: Soybean Epoxide Hydrolase Immobilized on UiO-66-NH 2 MOF for Efficient Biosynthesis of Enantiopure (R)-1,2-Octanediol in Deep Eutectic Solvents. ACS Sustain. Chem. Eng. 2016, 4, 3586–3595. [Google Scholar] [CrossRef]
- Koutsianos, A.; Kazimierska, E.; Barron, A.R.; Taddei, M.; Andreoli, E. A new approach to enhancing the CO2 capture performance of defective UiO-66 via post-synthetic defect exchange. Dalton Trans. 2019, 48, 3349–3359. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.; Debgupta, J.; Singh, C.; Sarkar, R.; Basu, O.; Das, S.K. Designing UiO-66-Based Superprotonic Conductor with the Highest Metal–Organic Framework Based Proton Conductivity. ACS Appl. Mater. Interfaces 2019, 11, 13423–13432. [Google Scholar] [CrossRef] [PubMed]
- Tu, J.; Zeng, X.; Xu, F.; Wu, X.; Tian, Y.; Hou, X.; Long, Z. Microwave-induced fast incorporation of titanium into UiO-66 metal–organic frameworks for enhanced photocatalytic properties. Chem. Commun. 2017, 53, 3361–3364. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.W.; Didriksen, T.; Olsbye, U.; Blom, R.; Grande, C.A. Shaping of metal-organic framework UiO-66 using alginates: Effect of operation variables. Sep. Purif. Technol. 2020, 235, 116182. [Google Scholar] [CrossRef]
- Rouquerol, J.; Rouquerol, F.; Llewellyn, P.; Denoyel, R. Molecular Sciences and Chemical Engineering. In Principles and Applications of Calorimetry; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 978-0-12-409547-2. [Google Scholar]
- Kirkham, M.B. Chapter 18—Thermocouple Psychrometers. In Principles of Soil and Plant Water Relations, 2nd ed.; Academic Press: Boston, MA, USA, 2014; pp. 311–331. ISBN 978-0-12-420022-7. [Google Scholar]
- Kaskel, S. Sorption Filter Material and Use Thereof. U.S. Patent 8,647,419, 11 February 2014. [Google Scholar]
- Formisano, B.; Bonten, C. Extruded zeolitic honeycombs for sorptive heat storage. AIP Conf. Proc. 2016, 1779, 30003. [Google Scholar] [CrossRef] [Green Version]
- Piepenbrock, M.-O.M.; Lloyd, G.O.; Clarke, N.; Steed, J.W. Metal- and Anion-Binding Supramolecular Gels. Chem. Rev. 2010, 110, 1960–2004. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X.; Wu, Y.; Li, D.-S.; Zhang, Q. Surfactants as promising media in the field of metal-organic frameworks. Coord. Chem. Rev. 2019, 391, 30–43. [Google Scholar] [CrossRef]
- Ramos-Fernandez, E.V.; Garcia-Domingos, M.; Juan-Alcañiz, J.; Gascon, J.; Kapteijn, F. MOFs meet monoliths: Hierarchical structuring metal organic framework catalysts. Appl. Catal. A Gen. 2011, 391, 261–267. [Google Scholar] [CrossRef]
- Gancarz, T. Density, surface tension and viscosity of liquid ZnAl + X (X = Li, Na, Si) alloys. Fluid Phase Equilib. 2016, 427, 97–103. [Google Scholar] [CrossRef]
- Hogness, T.R. The surface tensions and densities of liquid mercury, cadmium, zinc, lead, tin and bismuth. J. Am. Chem. Soc. 1921, 43, 1621–1628. [Google Scholar] [CrossRef]
- Allioux, F.-M.; Merhebi, S.; Tang, J.; Idrus-Saidi, S.A.; Abbasi, R.; Saborio, M.G.; Ghasemian, M.B.; Han, J.; Namivandi-Zangeneh, R.; O’Mullane, A.P.; et al. Catalytic Metal Foam by Chemical Melting and Sintering of Liquid Metal Nanoparticles. Adv. Funct. Mater. 2020, 30, 1907879. [Google Scholar] [CrossRef]
- Ramos-Fernandez, E.V.; Redondo-Murcia, A.; Grau-Atienza, A.; Sepúlveda-Escribano, A.; Narciso, J. Clean production of Zeolitic Imidazolate Framework 8 using Zamak residues as metal precursor and substrate. J. Clean. Prod. 2020, 260, 121081. [Google Scholar] [CrossRef]
- Salavagione, H.; Prieto, R.; Morallón, E.; Narciso, J. 3D Electrodes from aluminium foams prepared by replication process. J. Appl. Electrochem. 2010, 40, 241–246. [Google Scholar] [CrossRef] [Green Version]
- Combaz, E.; Mortensen, A. Fracture toughness of Al replicated foam. Acta Mater. 2010, 58, 4590–4603. [Google Scholar] [CrossRef]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook, Eighth Edition, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2008; ISBN 9780071422949. [Google Scholar]
- Garcia-Cordovilla, C.; Louis, E.; Narciso, J. Pressure infiltration of packed ceramic particulates by liquid metals. Acta Mater. 1999, 47, 4461–4479. [Google Scholar] [CrossRef]
- Pinto, H.; Silva, F.J.G. Optimisation of Die Casting Process in Zamak Alloys. Procedia Manuf. 2017, 11, 517–525. [Google Scholar] [CrossRef]
- Kang, N.; Na, H.S.; Kim, S.J.; Kang, C.Y. Alloy design of Zn–Al–Cu solder for ultra high temperatures. J. Alloys Compd. 2009, 467, 246–250. [Google Scholar] [CrossRef]
- Molina, J.M.; Arpón, R.; Saravanan, R.A.; Garcı́a-Cordovilla, C.; Louis, E.; Narciso, J. Threshold pressure for infiltration and particle specific surface area of particle compacts with bimodal size distributions. Scr. Mater. 2004, 51, 623–627. [Google Scholar] [CrossRef]
- Kolaczkowski, S.T.; Awdry, S.; Smith, T.; Thomas, D.; Torkuhl, L.; Kolvenbach, R. Potential for metal foams to act as structured catalyst supports in fixed-bed reactors. Catal. Today 2016, 273, 221–233. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. (Eds.) The mechanics of foams: Basic results. In Cellular Solids: Structure and Properties; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 1997; pp. 175–234. ISBN 9780521499118. [Google Scholar]
- Clyne, T.W. 4.7 Thermal and Electrical Conduction in Metal Matrix Composites; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier: Oxford, UK, 2018; pp. 188–212. ISBN 978-0-08-100534-7. [Google Scholar]
- Coutts, T.J. Percolation conduction in mixed insulator-conductor systems. Thin Solid Film 1976, 38, 313–321. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structures and Properties, 2nd ed.; Cambridge University Press Location: Cambridge, UK, 1997. [Google Scholar]
- Caccia, M.; Camarano, A.; Sergi, D.; Ortona, A.; Narciso, J. Wetting and Navier-Stokes Equation—The Manufacture of Composites Material in Wetting and Wettability; IntechOpen Limited: London, UK, 2015; pp. 105–137. [Google Scholar]
- Prieto, R.; Molina, J.M.; Narciso, J.; Louis, E. Thermal Conductivity of graphite flakes-SiC particles/metal composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 190–197. [Google Scholar] [CrossRef]
- Pastor-Blas, M.M.; Martín-Martínez, J.M.; Boerio, F.J. Influence of Chlorinating Solution Concentration on the Interactions Produced Between Chlorinated Thermoplastic Rubber and Polyurethane Adhesive at the Interface. J. Adhes. 2002, 78, 39–77. [Google Scholar] [CrossRef]
- Caccia, M.; Giuranno, D.; Molina-Jorda, J.M.; Moral, M.; Nowak, R.; Ricci, E.; Sobczak, N.; Narciso, J.; Sanz, J.F. Graphene Translucency and Interfacial Interactions in the Gold/Graphene/SiC System. J. Phys. Chem. Lett. 2018, 9, 3850–3855. [Google Scholar] [CrossRef] [PubMed]
- Calderón, N.R.; Martínez-Escandell, M.; Narciso, J.; Rodríguez-Reinoso, F. The role of carbon biotemplate densisty in mechanical properties of biomorphic SiC. J. Eur. Ceram. Soc. 2009, 29, 465–472. [Google Scholar] [CrossRef]
- Gibson, L.J. Ashby, M.F. Ashby Cellular Solids, Structure and Properties; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Despois, J.F.; Mueller, R.; Mortensen, A. Uniaxial deformation of microcellular metals. Acta Mater. 2006, 54, 4129. [Google Scholar] [CrossRef]
- Mortensen, A.; Conde, Y.; Rossoll, A. Sacalling of conductivitu and Young´s modulus in replicated microcellular materials. J. Mater. Sci. 2013, 48, 8140–8146. [Google Scholar] [CrossRef]





| Sample | He Density (g/cm3) | Porosity (%) | t/l | E (GPa) | σ (MSm−1) |
|---|---|---|---|---|---|
| 150 mm | 6.75 6.78 | 0.69 0.71 | 0.185 0.178 | 1.9 0.7 | 1.7 1.4 |
| 270 mm | 6.77 6.81 | 0.695 0.73 | 0.183 0.172 | 1.4 0.46 | 1.4 1.2 |
| 420 mm | 6.79 6.78 6.80 | 0.705 0.715 0.72 | 0.179 0.175 0.174 | 0.962 0.586 0.501 | 1.2 1.3 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado-Marín, J.J.; Izan, D.P.; Molina-Sabio, M.; Ramos-Fernandez, E.V.; Narciso, J. New Generation of MOF-Monoliths Based on Metal Foams. Molecules 2022, 27, 1968. https://doi.org/10.3390/molecules27061968
Delgado-Marín JJ, Izan DP, Molina-Sabio M, Ramos-Fernandez EV, Narciso J. New Generation of MOF-Monoliths Based on Metal Foams. Molecules. 2022; 27(6):1968. https://doi.org/10.3390/molecules27061968
Chicago/Turabian StyleDelgado-Marín, José J., Dennis P. Izan, Miguel Molina-Sabio, Enrique V. Ramos-Fernandez, and Javier Narciso. 2022. "New Generation of MOF-Monoliths Based on Metal Foams" Molecules 27, no. 6: 1968. https://doi.org/10.3390/molecules27061968
APA StyleDelgado-Marín, J. J., Izan, D. P., Molina-Sabio, M., Ramos-Fernandez, E. V., & Narciso, J. (2022). New Generation of MOF-Monoliths Based on Metal Foams. Molecules, 27(6), 1968. https://doi.org/10.3390/molecules27061968