Adsorption of Chromium and Nickel Ions on Commercial Activated Carbon—An Analysis of Adsorption Kinetics and Statics
Abstract
:1. Introduction
2. Results and Discussion
2.1. Adsorption of Cr(III) Ions
2.1.1. Adsorption Kinetics
| Model | Parameter | WG-12 | ROW | F-300 |
|---|---|---|---|---|
| Pseudo-first order | qmax (mg/g) | 43.32 | 51.42 | 42.32 |
| k1 (h−1) | 1.588 | 2.254 | 1.236 | |
| R2 | 0.935 | 0.947 | 0.967 | |
| E, % | 3.51 | 2.05 | 3.29 | |
| Pseudo-second order | qmax (mg/g) | 49.30 | 54.36 | 47.27 |
| k2 (h−1) | 0.050 | 0.077 | 0.036 | |
| R2 | 0.996 | 0.989 | 0.996 | |
| E, % | 0.84 | 0.87 | 1.05 | |
| Elovich | α, mg/(g·h) | 821 | 15929 | 298 |
| β, g/mg | 0.148 | 0.186 | 0.125. | |
| R2 | 0.954 | 0.878 | 0.950 | |
| E, % | 3.12 | 3.33 | 4,43 | |
Intraparticle diffusion model (Weber–Morris) | kp1, mg/(g·h0.5) | 18.02 | 17.39 | 21.32 |
| C1, mg/g | 13.92 | 25.00 | 7.11 | |
| R2 | 0.926 | 0.958 | 0.940 | |
| kp2, mg/(g·h0.5) | 3.50 | 0.62 | 3.72 | |
| C2, mg/g | 35.52 | 50.42 | 33.665 | |
| R2 | 0.938 | 0.993 | 0.919 |
| Activated Carbon | Max. qm, mg/g | Adsorption Isotherms Equations Tested | The Equations of Adsorption Kinetics Studied | Ref. |
|---|---|---|---|---|
| From corncob waste | 84.64 | L > F | PSO > PFO | [41] |
| From macadamia | 69.61 | F > L | PSO > PFO | [35] |
| From wood | 185.18 | L > F > T > D–R | PSO > PFO | [40] |
| From leather industry solid wastes | 220 | T > F > L | PSO > Elovich > IDP > PFO | [42] |
| From olive waste | 12.46 | L = T > F | PSO > PFO | [43] |
| From fish scale | 18.34 | L > F | PSO > PFO | [44] |
| From cordia africana | 0.011 | F > L | PFO > PSO | [27] |
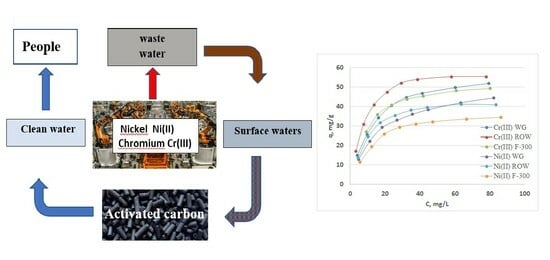
2.1.2. Adsorption Statics
- -
- On amphoteric and basic activated carbons:
- -
- On “acidic” activated carbon:
| Parameter | Unit | Activated Carbon | ||
|---|---|---|---|---|
| WG-12 | ROW 08 | F-300 | ||
| Bulk density (PN-EN 12915) | g/dm3 | 424 ± 27 | 381 ± 16 | 542 ± 36 |
| Surface area (BET) | m2/g | 1098 ± 38 | 897 ± 30 | 847 ± 29 |
| pH of the water extract (PN-82/C-97555) | - | 6.7 | 8.6 | 6.8 |
| Pore structure Vtotal Vmacr Vmezo. Vmicr. | cm3/g cm3/g cm3/g cm3/g | 0.990 0.400 0.066 0.524 | 1.135 0.246 0.453 0.436 | 0.987 0.217 0.294 0.476 |
| Iodine adsorption, LI (PN-EN 12902) | mg/g | 1050 | 1096 | 1065 |
| Methylene blue number, LM (PN-82/C-97555.03) | cm3 | 30 | 30 | 28 |
| Grain composition—sieve analysis (PN-EN 12902) >2.0 mm 2.0 ÷ 1.5 mm 1.5 ÷ 1.0 mm 1.0 ÷ 0.5 mm <0.5 mm | % | 4.9 57.4 34.3 2.2 1.0 | 36.4 41.2 21.7 0.3 0.1 | 31.4 23.4 30.2 10.2 4.6 |
| Activated Carbon | WG-12 | ROW 08 | F-300 | |
|---|---|---|---|---|
| Isoelectric Point, pHPZC | - | 6.4 | 6.5 | 6.6 |
| Acidic groups (Boehm method) Carboxylic groups -COOH Lactonic group -COO- Phenolic groups -OH Carbonyl groups =CO Basic groups/sites | mmol/g | 0.586 0.182 0.209 0.110 0.085 0.467 | 0.434 0.063 0.120 0.409 0.021 0.592 | 0.544 0.138 0.048 0.316 0.060 0.512 |
2.2. Adsorption of Ni(II) Ions
2.2.1. Adsorption Kinetics
2.2.2. Adsorption Statics
2.3. Adsorption of Tested Ions from Natural Waters
2.4. Mechanism of Adsorption of Cr(III) and Ni(II) Cations
3. Materials and Methods
3.1. Adsorbents Used in this Research
3.2. Solutions of Heavy Metals Used in this Research
3.3. Adsorption Kinetics and Statics Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balali-Mood, M.; Naseri, K.; Tahergorabi, Z.; Khazdair, M.R.; Sadeghi, M. Toxic mechanisms of five heavy metals: Mercury, Lead, Chromium, Cadmium and Arsenic. Front. Pharmacol. 2021, 12, 227. [Google Scholar] [CrossRef] [PubMed]
- Bibaj, E.; Lysigaki, K.; Nolan, J.W.; Seyedsalehi, M.; Deliyanni, E.A.; Mitropoulos, A.C.; Kyzas, G.Z. Activated carbons from banana peels for the removal of nickel ions. Int. J. Environ. Sci. Technol. 2019, 16, 667–680. [Google Scholar] [CrossRef]
- El-Sadaawy, M.; Abdelwahab, O. Adsorptive removal of nickel from aqueous solutions by activated carbons from doum seed (Hyphaenethebaica) coat Manal. Alex. Eng. J. 2014, 53, 399–408. [Google Scholar] [CrossRef]
- Rehmana, K.; Fatima, F.; Waheed, I.; Akash, M.S.H. Prevalence of exposure of heavy metals and their impact on health consequences. J. Cell Biochem. 2018, 119, 157–184. [Google Scholar] [CrossRef]
- Guidelines for Drinking Water Quality Recommendations; World Health Organization: Geneva, Switzerland, 2017.
- Vieira, M.G.A.; Almeida Neto, A.F.; Gimenes, M.L.; da Silva, M.G.C. Sorption kinetics and equilibrium for the removal of nickel ions from aqueous phase on calcined Bofe bentonite clay. J. Hazard. Mater. 2020, 177, 362–371. [Google Scholar] [CrossRef]
- Begum, W.; Rai, S.; Banerjee, S.; Bhattacharjee, S.; Mondal, M.H.; Bhattarai, A.; Saha, B. A comprehensive review on the sources, essentiality and toxicological profile of nickel. RSC Adv. 2022, 12, 9139–9153. [Google Scholar] [CrossRef] [PubMed]
- Lakherwal, D. Adsorption of heavy metals: A review. Int. J. Environ. Res. Dev. 2014, 4, 41–48. [Google Scholar] [CrossRef]
- Costa, F.; Tavares, T. Bioremoval of Ni and Cd in the presence of diethylketone by fungi and by bacteria—A comparative study. IBBS 2017, 120, 115–123. [Google Scholar] [CrossRef]
- Lindsay, D.R.; Farley, K.J.; Carbonaro, R.F. Oxidation of CrIII to CrVI during chlorination of drinking water. J. Environ. Monitor. 2012, 7, 1789–1797. [Google Scholar] [CrossRef]
- Imanaka, S.; Hayashi, H. Behavior of hexavalent chromium in the water supply system by IC-ICP-MS method. Water Supply 2013, 13, 96–103. [Google Scholar] [CrossRef]
- Chebeir, M.; Liu, H. Kinetics and mechanisms of Cr(VI) formation via the oxidation of Cr(III) solid phases by chlorine in drinking water. Environ. Sci. Technol. 2016, 50, 701–710. [Google Scholar] [CrossRef] [PubMed]
- Katsoyiannis, I.A.; Gachet, C.; von Gunten, U. Fate of Cr(III) during ozonation of secondary municipal wastewater effluent. Ozone Sci. Eng. 2018, 40, 441–447. [Google Scholar] [CrossRef]
- Arellano-Sánchez, M.G.; Devouge-Boyer, C.; Hubert-Roux, M.; Afonso, C.; Mignot, M. Quantitative extraction of chromium VI and III from garbned leather: A comparative study of pretreatment methods. Crit. Rev. Anal. Chem. 2022, 52, 1537–1556. [Google Scholar] [CrossRef] [PubMed]
- Khedri, A.; Jafari, D.; Esfandyari, M. Adsorption of Nickel(II) ions from synthetic wastewater using activated carbon prepared from Mespilus germanica Lea. Arab. J. Sci. Eng. 2022, 47, 6155–6166. [Google Scholar] [CrossRef]
- Report on the State of the Footwear Industry in Poland; Poland Leather Industry: Łódź, Poland, 2023.
- Kahu, S.S.; Shekhawat, A.; Saravanan, D.; Jugade, R.M. Two fold modified chitosan for enhanced adsorption of hexavalent chromium from simulated wastewater and industrial effluents. Carbohydr. Polym. 2016, 146, 264–273. [Google Scholar] [CrossRef] [PubMed]
- Vasudevan, M.; Ajithkumar, P.S.; Singh, R.P.; Natarajan, N. Mass transfer kinetics using two-site interface model for removal of Cr (VI) from aqueous solution with cassava peel and rubber tree bark as adsorbents. Environ. Eng. Res. 2016, 21, 152–163. [Google Scholar] [CrossRef]
- Oncel, M.S.; Muhcu, A.; Demirbas, E.; Kobya, M. A comparative study of chemical precipitation and electrocoagulation for treatment of coal acid drainage wastewater. J. Environ. Chem. Eng. 2013, 1, 989–995. [Google Scholar] [CrossRef]
- Qasem, N.A.A.; Mohammed, R.H.; Lawal, D.U. Removal of heavy metal ions from wastewater: A comprehensive and critical review. Clean. Water 2021, 4, 36. [Google Scholar] [CrossRef]
- Karimi-Maleh, H.; Ayati, A.; Ghanbari, S.; Orooji, Y.; Tanhaei, B.; Karimi, F.; Alizadeh, M.; Rouhi, J.; Fu, L.; Sillanpää, M. Recent advances in removal techniques of Cr(VI) toxic ion from aqueous solution: A comprehensive review. J. Mol. Liq. 2021, 329, 115062. [Google Scholar] [CrossRef]
- Ianăşi, C.; Ianăşi, P.; Negrea, A.; Ciopec, M.; Ivankov, O.I.; Kuklin, A.I.; Almásy, L.; Putz, A.M. Effects of catalysts on structural and adsorptive properties of iron oxide-silica nanocomposites. Kor. J. Chem. Eng. 2021, 38, 292–305. [Google Scholar] [CrossRef]
- Liakos, E.V.; Mone, M.; Lambropoulou, D.A.; Bikiaris, D.N.; Kyzas, G.Z. Adsorption evaluation for the removal of nickel, mercury, and barium ions from single-component and mixtures of aqueous solutions by using an optimized biobased chitosan derivative. Polymers 2021, 13, 232. [Google Scholar] [CrossRef]
- Lakshmipathy, R.; Sarada, N.C. Application of watermelon rind as sorbent for removal of Nickel and Cobalt from aqueous solution. Int. J. Miner. Process. 2013, 122, 63–65. [Google Scholar] [CrossRef]
- Aranda-García, E.; Cristiani-Urbina, E. Kinetic, equilibrium, and thermodynamic analyses of Ni(II) biosorption from aqueous solution by acorn shell of Quercus crassipes. Water Air Soil Pollut. 2018, 229, 119. [Google Scholar] [CrossRef]
- Flores-Garnica, J.G.; Morales-Barrera, L.; Pineda-Camacho, G.; Cristiani-Urbina, E. Biosorption of Ni(II) from aqueous solutions by Litchi chinensis seeds. Bioresour. Technol. 2013, 136, 635–643. [Google Scholar] [CrossRef] [PubMed]
- Kassahun, E.; Fito, J.; Tibebu, S.; Nkambule, T.T.I.; Tadesse, T.; Sime, T.; Kloos, H. The application of the activated carbon from Cordia africana leaves for adsorption of Chromium (III) from an aqueous solution. J. Chem. 2022, 17, 4874502. [Google Scholar] [CrossRef]
- Samaraweera, A.P.G.M.V.; Priyantha, N.; Gunathilake, W.S.S.; Kotabewatta, P.A.; Kulasooriya, T.P.K. Biosorption of Cr (III) and Cr (VI) species on NaOH-modified peel of Artocarpus nobilis fruit. 1. Investigation of kinetics. Appl. Water Sci. 2020, 10, 115. [Google Scholar] [CrossRef]
- Castro-Castro, J.D.; Macías-Quiroga, I.F.; Giraldo-Gómez, G.I.; Sanabria-González, N.R.; Sanabria-González, N.R. Adsorption of Cr (VI) in aqueous solution using a surfactant-modified bentonite. Sci. World J. 2020, 2020, 3628163. [Google Scholar] [CrossRef]
- Kaźmierczak, B.; Molenda, J.; Swat, M. The adsorption of chromium (III) ions from water solutions on biocarbons obtained from plant waste. Environ. Technol. Innov. 2021, 23, 101737. [Google Scholar] [CrossRef]
- Bautista-Toledo, A.I.; Rivera-Utrilla, J.; Ocampo-Perez, R.; Carrasco-Marin, F.; Sanchez-Polo, M. Cooperative adsorption of bisphenol-A and chromium(III) ions from water on activated carbons prepared from olive-mill waste. Carbon 2014, 73, 338–350. [Google Scholar] [CrossRef]
- Duran, C.; Ozdes, D.; Gundogdu, A.; Imamoglu, M.; Senturk, H.B. Tea-industry waste activated carbon, as a novel adsorbent, for separation, preconcentration and speciation of chromium. Anal. Chim. Acta 2011, 688, 75–83. [Google Scholar] [CrossRef]
- Gupta, V.K.; Ali, I.; Seleh, T.A.; Siddigui, M.N.; Agawal, S. Chromium removal from water by activated carbon developed from waste rubber tires. Environ. Sci. Pollut. Rep. 2013, 20, 1261–1268. [Google Scholar] [CrossRef] [PubMed]
- Manilo, M.V.; Choma, Z.Z.; Barany, S. Comparative study of Cr(III) adsorption by carbon nanotubes and active carbons. Colloid. J. 2017, 79/2, 212–218. [Google Scholar] [CrossRef]
- Lesaoana, M.; Pakade, V.E.; Chimuka, L. Crosslinker-less surface-imprinted Macadamia derived activated carbons for trace Cr(III) removal from aqueous solution. Environ. Technol. Innov. 2019, 14, 100336. [Google Scholar] [CrossRef]
- Tran, H.N.; You, S.-J.; Hosseini-Bandegharaei, A.; Chao, H.-P. Mistakes and inconsistencies regarding adsorption of contaminants from aqueous solutions: A critical review. Water Res. 2017, 120, 88–116. [Google Scholar] [CrossRef] [PubMed]
- Płaziński, W.; Rudziński, W. Adsorption kinetics at solid/solution interfaces the meaning of the pseudo-first- and pseudo-second-order equations. Chem. News 2011, 65, 1055–1067. Available online: http://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-article-BUS8-0017-0041 (accessed on 1 September 2023).
- Borysiak, M.; Gabruś, E. Adsorptive removal of cochineal red a dye from aqueous solutions using yeast. Chem. Process Eng. 2020, 41, 105–117. [Google Scholar] [CrossRef]
- Sun, L.; Chen, D.; Wan, S.; Yu, Z. Performance, kinetics, and equilibrium of methylene blue adsorption on biochar derived from eucalyptus saw dust modified with citric, tartaric, and acetic acids. Bioresour. Technol. 2015, 198, 300–308. [Google Scholar] [CrossRef]
- Wei, X.; Wu, Z.; Wu, Z.; Ye, B.-C. Adsorption behaviors of atrazine and Cr(III) onto different activated carbons in single and co-solute systems. Powder Technol. 2018, 329, 207–216. [Google Scholar] [CrossRef]
- Fonseca-Correa, R.; Giraldo, L.; Moreno-Pirajan, J.C. Trivalent chromium removal from aqueous solution with physically and chemically modified corncob waste. J. Anal. Appl. Pyrol. 2013, 101, 132–141. [Google Scholar] [CrossRef]
- Jimenez-Paz, J.; Lozada-Castro, J.J.; Lester, E.; Williams, O.; Stevens, L.; Barraza-Burgos, J. Solutions to hazardous wastes issues in the leather industry: Adsorption of Chromium III and vi from leather industry wastewaters using activated carbons produced from leather industry solid wastes. J. Environ. Chem. Eng. 2023, 11, 109715. [Google Scholar] [CrossRef]
- Ba, S.; Ennaciri, K.; Yaacoubi, A.; Alagui, A.; Bacaoui, A. Activated carbon from olive wastes as an adsorbent for chromium ions removal. Iran. J. Chem. Chem. Eng. 2018, 37/6, 107–123. [Google Scholar] [CrossRef]
- Teshale, F.; Karthikeyan, R.; Sahu, O. Synthesized bioadsorbent from fish scale for chromium (III) removal. Micron 2020, 130, 102817. [Google Scholar] [CrossRef]
- Lach, J.; Ociepa-Kubicka, A.; Mrowiec, M. Oxytetracycline adsorption from aqueous solutions on commercial and high-temperature modified activated carbons. Energies 2021, 14, 3481. [Google Scholar] [CrossRef]
- Nerm, A.E.; Aboughaly, R.M.; Sikaily, A.E.; Masoud, M.S.; Ramadan, M.S.; Ragab, S. Microporous-activated carbons of type I adsorption isotherm derived from sugarcane bagasse impregnated with zinc chloride. Carbon. Lett. 2022, 2, 229–249. [Google Scholar] [CrossRef]
- Lach, J. Adsorption of sulfacetamide on commercial activated carbons: Statistics and kinetics of adsorption. Desalin. Water Treat. 2022, 274, 173–186. [Google Scholar] [CrossRef]
- Lach, J.; Szymonik, A. Adsorption of diclofenac sodium from aqueous solutions on commercial activated carbons. Desalin. Water Treat. 2020, 186, 418–429. [Google Scholar] [CrossRef]
- Kim, Y.; Bae, J.; Park, H.; Suh, J.-K.; You, Y.-W.; Choi, H. Adsorption dynamics of methyl violet onto granulated mesoporous carbon: Facile synthesis and adsorption kinetics. Water Res. 2016, 101, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Halder, G.; Khan, A.A.; Dhawane, S. Fluoride sorption onto a steam-activated biochar derived from cocos nucifera shell. CLEAN-Soil Air Water 2016, 44, 124–133. [Google Scholar] [CrossRef]
- Çalişkan, Ç.E.; Çiftçi, H.; Çiftçi, T.; Kariptaş, E.; Arslanoğlu, H.; Erdem, M. Use of activated carbon obtained from waste vine shoots in nickel adsorption in simulated stomach mediu. Biomass Convers. Biorefinery 2023, 13, 2391–2400. [Google Scholar] [CrossRef]
- Manjuladevi, M.; Anitha, R.; Manonmani, S. Kinetic study on adsorption of Cr(VI), Ni(II), Cd(II) and Pb(II) ions from aqueous solutions using activated carbon prepared from Cucumis melo peel. Appl. Water Sci. 2018, 8, 36. [Google Scholar] [CrossRef]
- Krishnan, K.A.; Sreejalekshmi, K.G.; Baiju, R.S. Nickel(II) adsorption onto biomass based activated carbon obtained from sugarcane bagasse pith. Bioresour. Technol. 2011, 102, 10239–10247. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Guo, Z.; Zhang, J.; Xie, H.; Liu, H.; Zhang, C. Enhancement of Ni(II) removal by urea-modified activated carbon derived from Pennisetum alopecuroides with phosphoric acid activation. J. Taiwan. Inst. Chem. Eng. 2016, 60, 335–341. [Google Scholar] [CrossRef]
- Bartczak, P.; Norman, M.; Klapiszewski, Ł.; Karwańska, N.; Kawalec, M.; Baczyńska, M.; Wysokowski, M.; Zdarta, J.; Ciesielczyk, F.; Jesionowski, T. Removal of nickel(II) and lead(II) ions from aqueous solution using peat as a low-cost adsorbent: A kinetic and equilibrium study. Arab. J. Chem. 2018, 11, 1209–1222. [Google Scholar] [CrossRef]
- Aboli, E.; Jafari, D.; Esmaeili, H. Heavy metal ions (lead, cobalt, and nickel) biosorption from aqueous solution onto activated carbon prepared from Citrus limetta leaves. Carbon. Lett. 2020, 30, 683–698. [Google Scholar] [CrossRef]
- Gonsalvesh, L.; Marinov, S.P.; Gryglewicz, G.; Carleer, R.; Yperman, J. Preparation, characterization and application of polystyrene based activated carbons for Ni(II) removal from aqueous solution. Fuel Process. Technol. 2016, 149, 75–85. [Google Scholar] [CrossRef]
- El-Maged, M.O.A.; Hassan, A.M.A.; Gad, H.M.H.; Mahammaden, T.F.; Youssef, M.A.M. Removal of nickel (II) ions from aqueous solutions using modified activated carbon: A kinetic and equilibrium study. J. Dispers. Sci. Technol. 2018, 39/6, 862–873. [Google Scholar] [CrossRef]
- Runtti, H.; Tuomikoski, S.; Kangas, T.; Lassi, U.; Kuokkanen, T.; Ramo, J. Chemically activated carbon residue from biomass gasification as a sorbent for iron(II), copper(II) and nickel(II) ions. J. Water Process Eng. 2014, 4, 12–24. [Google Scholar] [CrossRef]
- Nnaji, C.C.; Agim, A.E.; Mama, C.N.; Emenike, P.G.C.; Ogarekpe, N.M. Equilibrium and thermodynamic investigation of biosorption of nickel from water by activated carbon made from palm kernel chaff. Sci. Rep. 2021, 11, 7808. [Google Scholar] [CrossRef] [PubMed]
- Bouhamed, F.; Elouear, Z.; Bouzid, J.; Ouddane, B. Multi-component adsorption of copper, nickel and zinc from aqueous solutions onto activated carbon prepared from date Stones. Environ. Sci. Pollut. Res. 2016, 23, 15801–15806. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, B.; Gao, Y.; Xu, X.; Li, Q.; Wang, Y. Adsorption and cosorption of ciprofloxacin and Ni(II) on activated carbon-mechanism study. J. Taiwan. Inst. Chem. Eng. 2014, 45/2, 681–688. [Google Scholar] [CrossRef]
- Guo, Z.; Fan, J.; Zhang, J.; Kang, Y.; Liu, H.; Jiang, L.; Zhang, C. Sorption heavy metal ions by activated carbons with well-developed microporosity and amino groups derived from Phragmites australis by ammonium phosphates activation. J. Taiwan. Inst. Chem. Eng. 2016, 58, 290–296. [Google Scholar] [CrossRef]
- Li, G.; Wang, M.; Huang, J.; Bao, N.; Xue, J.; Liu, Q.; Huang, L. Preparation of activated carbon from Iris tectorum with different ammonium phosphates activation and removal of nickel from aqueous solution. J. Taiwan. Inst. Chem. Eng. 2016, 59, 341–347. [Google Scholar] [CrossRef]
- Sheng, P.X.; Ting, Y.-P.; Chen, J.P.; Hong, L. Sorption of lead, copper, cadmium, zinc, and nickel by marine algal biomass: Characterization of biosorptive capacity and investigation of mechanisms. J. Colloid. Interface Sci. 2004, 275/1, 131–141. [Google Scholar] [CrossRef]
- Dash, B.; Jena, S.K.; Rath, S.S. Adsorption of Cr (III) and Cr (VI) ions on muscovite mica: Experimental and molecular modeling studies. J. Mol. Liq. 2022, 357, 119116. [Google Scholar] [CrossRef]
- Saleh, T.A. Kinetic models and thermodynamics of adsorption processes: Classification. Interf. Sci. Technol. 2022, 34, 65–97. [Google Scholar] [CrossRef]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and interpretation of adsortion isotherms. J. Chem. 2017, 3039817. [Google Scholar] [CrossRef]









| Isotherm Model | Activated Carbon | Constants of the Isotherm Model | Model Accuracy Parameters | |||
|---|---|---|---|---|---|---|
| Langmuir | qm, mg/g | KL, L/mg | RL 1 | R2 | E, % | |
| WG-12 | 60.73 | 0.08 | 0.88–0.97 | 0.997 | 1.42 | |
| ROW 08 | 63.49 | 0.129 | 0.83–0.98 | 0.988 | 3.44 | |
| F-300 | 55.85 | 0.106 | 0.84–0.98 | 0.996 | 1.98 | |
| Freundlich | 1/n, - | KF, mg/g | - | R2 | E, % | |
| WG-12 | 0.341 | 12.58 | 0.929 | 9.97 | ||
| ROW 08 | 0.279 | 18.32 | 0.863 | 12.78 | ||
| F-300 | 0.298 | 14.41 | 0.907 | 10.24 | ||
| Temkin | A, L/mg | B, - | R2 | E, % | ||
| WG-12 | 0.817 | 13.026 | 0.999 | 0.31 | ||
| ROW 08 | 1.547 | 12.697 | 0.995 | 0.59 | ||
| F-300 | 1.202 | 11.451 | 0.998 | 0,. | ||
| Jovanovic | Kj, L/mg | qm, mg/g | R2 | E, % | ||
| WG-12 | 0.071 | 50.51 | 0.992 | 3.14 | ||
| ROW 08 | 0.104 | 54.94 | 0.997 | 2.01 | ||
| F-300 | 0.088 | 47.65 | 0.990 | 3.10 | ||
| Halsey | Kh, (mg·g−1/mg·L−1 | n, - | R2 | E, % | ||
| WG-12 | 192,276 | 4.196 | 0.855 | 14.74 | ||
| ROW 08 | 192,276 | 4.034 | 0.854 | 13.73 | ||
| F-300 | 192,276 | 4.214 | 0.874 | 12.32 | ||
| Redlich–Peterson | KR, L/g | aR, (L/mg)β | β | R2 | E, % | |
| WG-12 | 219,670 | 17,460 | 0.659 | 0.929 | 9.97 | |
| ROW 08 | 220,093 | 12,010 | 0.721 | 0.863 | 12.78 | |
| F-300 | 219,915 | 15,263 | 0.702 | 0.970 | 10.24 | |
| Toth | qm, mg/g | b, mg/g | v, - | R2 | E, % | |
| WG-12 | 68.90 | 0.092 | 0.773 | 0.992 | 2.94 | |
| ROW 08 | 57.90 | 0.097 | 1.524 | 0.998 | 1.35 | |
| F-300 | 52.42 | 0.90 | 1.264 | 0.999 | 0.85 | |
| Parameter | WG-12 | ROW | F-300 | |
|---|---|---|---|---|
| Pseudo-first order | qmax (mg/g) | 35.66 | 37.73 | 30.96 |
| k1 (h−1) | 0.986 | 0.965 | 0.751 | |
| R2 | 0.967 | 0.973 | 0.989 | |
| E, % | 3.77 | 3.67 | 3.06 | |
| Pseudo-second order | qmax (mg/g) | 40.68 | 43.16 | 36.61 |
| k2 (h−1) | 0.031 | 0.029 | 0.024 | |
| R2 | 0.996 | 0.997 | 0.996 | |
| E, % | 1.13 | 0.95 | 1.26 | |
| Elovich | α, mg/(g·h) | 135 | 135 | 60 |
| β, g/mg | 0.129 | 0.120 | 0.123 | |
| R2 | 0.969 | 0.968 | 0.971 | |
| E, % | 3.63 | 3.88 | 4.56 | |
| Intraparticle diffusion model (Weber–Morris) | kp1, mg/(g·h0.5) | 14.23 | 16.77 | 15.18 |
| C1, mg/g | 7.37 | 5.84 | 1.00 | |
| R2 | 0.976 | 0.978 | 0.983 | |
| kp2, mg/(g·h0.5) | 1.98 | 2.38 | 2.42 | |
| C2, mg/g | 31.10 | 32.10 | 24.71 | |
| R2 | 0.999 | 0.881 | 0.933 |
| Activated Carbon | Max. qm, mg/g | Adsorption Isotherms Equations Tested | The Equations of Adsorption Kinetics Studied | Ref. |
|---|---|---|---|---|
| Peat | 61.27 | L > F | PSO > PFO | [55] |
| From Mespilus germanica Lea | 13.08 | L > F | PSO > PFO | [15] |
| From Citrus limetta leaves | 58.14 | L > F | PSO > PFO | [56] |
| Polystyrene based | 40.82 | L > F | PSO > IPD > Elovich > PFO | [57] |
| Modified AC | 56.18 | L > T > F > D–R | PSO > PFO > Elovich | [58] |
| From biomass | 62.9 | L > F > D–R | PSO | [59] |
| From palm kernel chaff | 115.7 | L ≈ T ≈ D–R > F | PSO > PFO | [60] |
| From date stones | 16.12 | L ≥ F | - | [61] |
| From arundo donax | 8.61 | F > L | PSO > PFO > IPD | [62] |
| Isotherm Model | Activated Carbon | Constants of the Isotherm Model | Model Accuracy Parameters | |||
|---|---|---|---|---|---|---|
| Langmuir | qm, mg/g | KL, L/mg | RL | R2 | E, % | |
| WG-12 | 51.70 | 0.067 | 0.88–0.99 | 0.998 | 1.15 | |
| ROW 08 | 47.48 | 0.104 | 0.82–0.98 | 0.986 | 3.44 | |
| F-300 | 40.29 | 0.082 | 0.83–0.98 | 0.987 | 3.58 | |
| Freundlich | 1/n, - | KF, mg/g | - | R2 | E, % | |
| WG-12 | 0.361 | 9.497 | 0.960 | 7.25 | ||
| ROW 08 | 0.286 | 12.74 | 0.869 | 11.14 | ||
| F-300 | 0.312 | 9.30 | 0.888 | 10.68 | ||
| Temkin | A, L/mg | B, - | R2 | E, % | ||
| WG-12 | 0.677 | 11.21 | 0.999 | 0.13 | ||
| ROW 08 | 1.189 | 9.71 | 0.996 | 0.54 | ||
| F-300 | 0.838 | 8.59 | 0.997 | 0.49 | ||
| Jovanovic | Kj, L/mg | qm, mg/g | R2 | E, % | ||
| WG-12 | 0.061 | 42.45 | 0.978 | 5.04 | ||
| ROW 08 | 0.087 | 40.61 | 0.997 | 1.42 | ||
| F-300 | 0.071 | 33.82 | 0.997 | 1.65 | ||
| Halsey | Kh, (mg·g−1/mg·L−1 | n, - | R2 | E, % | ||
| WG-12 | 192,276 | 4.43 | 0.841 | 14.37 | ||
| ROW 08 | 192,276 | 4.41 | 0.836 | 13.22 | ||
| F-300 | 192,276 | 4.69 | 0.808 | 14.00 | ||
| Redlich–Peterson | KR, L/g | aR, (L/mg)β | β | R2 | E, % | |
| WG-12 | 219,372 | 23,097 | 0.639 | 0.960 | 7.25 | |
| ROW 08 | 219,986 | 17,262 | 0.714 | 0.869 | 11.14 | |
| F-300 | 219,489 | 23,600 | 0.688 | 0.888 | 10.68 | |
| Toth | qm, mg/g | b, mg/g | v, - | R2 | E, % | |
| WG-12 | 54.67 | 0.073 | 0.878 | 0.999 | 1.01 | |
| ROW 08 | 42.56 | 0.077 | 1.627 | 0.999 | 0.52 | |
| F-300 | 35.64 | 0.062 | 1.632 | 0.998 | 1.39 | |
| Water | Water Composition, mg/L | Adsorption Efficiency, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Anions | Cations | |||||||||
| F− | Cl− | Ca2+ | Mg2+ | Na+ | K+ | Cr(III) | Ni(II) | |||
| Demineralized | - | - | - | - | - | - | - | - | 61.5 ± 0.7 | 54.2 ± 1.0 |
| Spring water (A) | 131.06 | - | 0.07 | - | 41.69 | 5.62 | 9.65 | - | 60.4 ± 2.3 | 53.9 ± 0.8 |
| Spring water (B) | 180.90 | 14.82 | 0.12 | 3.19 | 46.09 | 8.51 | 6.25 | 2.00 | 59.7 ± 1.2 | 53.5 ± 1.1 |
| Spring water (C) | 216.60 | 10.90 | - | 4.96 | 71.14 | 5.47 | 1.87 | 0.50 | 58.6 ± 2.5 | 52.3 ± 1.4 |
| Spring water (D) | 168.00 | 14.71 | 0.09 | 2.80 | 50.10 | 6.08 | 2.50 | 1.19 | 58.3 ± 2.4 | 52.1 ± 2.3 |
| Low mineralized (E) | 186.70 | 43.62 | - | 3.19 | 44.09 | 17.01 | 11.10 | 1.00 | 57.7 ± 2.8 | 51.9 ± 2.1 |
| Medium mineralized (E) | 299.00 | 41.60 | 0.23 | - | 91.18 | 16.52 | 6.44 | 1.21 | 56.3 ± 1.8 | 50.7 ± 2.5 |
| Medium mineralized (F) | 432.7 | - | 0.23 | 2.50 | 102.2 | 16.00 | 11.25 | 2.34 | 55.8 ± 2.1 | 50.3 ± 2.6 |
| Highly mineralized (G) | 1403.7 | 32.0 | - | 7.0 | 180.9 | 142.7 | 63.0 | 7.5 | 48.3 ± 3.5 | 43.0 ± 3.2 |
| Spectrum | C | O | Na | Mg | Al | Si | S | K | Ca | Cr | Fe | Ni |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F-300 | 66.32 | 29.92 | - | - | 1.18 | 1.14 | 0.85 | - | - | - | 0.59 | - |
| 63.72 | 31.70 | - | - | 1.53 | 1.51 | 0.73 | - | - | - | 0.80 | - | |
| 66.15 | 29.98 | - | - | 1.24 | 1.24 | 0.83 | - | - | - | 0.56 | - | |
| ROW 08 Supra | 70.10 | 26.00 | - | - | 0.57 | 0.98 | 0.80 | - | 0.87 | - | 0.74 | - |
| 72.68 | 24.66 | - | - | 0.34 | 0.44 | 0.75 | - | 0.56 | - | 0.55 | - | |
| 72.20 | 25.15 | - | - | 0.33 | 0.52 | 0.75 | - | 0.52 | - | 0.52 | - | |
| WG-12 | 51.13 | 38.88 | - | - | 0.90 | 6.70 | 0.20 | 0.54 | - | - | 1.08 | - |
| 45.75 | 42.56 | - | - | 3.40 | 4.89 | 0.27 | 0.50 | - | - | 1.83 | - | |
| 48.63 | 40.88 | - | - | 2.88 | 4.18 | 0.27 | 0.56 | - | - | 1.78 | - |
| Process | Adsorption Time, h | Initial Concentration, mg/L | Sample Volume, L | pH of the Solution | Activated Carbon Dose, g/L |
|---|---|---|---|---|---|
| Adsorption kinetics | 0.5, 1, 2, 3, 4, 5, 6, 7 and 8 | 50 | 0.250 | 6 ± 0.2 | 0.4 |
| Statics of adsorption | 6 | 10, 20, 30, 40, 50, 60, 80 and 100 | 0.250 | 6 ± 0.2 | 0.4 |
| Influence of adsorption dose | 6 | 100 | 0.250 | 6 ± 0.2 | 0.5, 1, 2, 3, 4, 5 and 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lach, J.; Okoniewska, E. Adsorption of Chromium and Nickel Ions on Commercial Activated Carbon—An Analysis of Adsorption Kinetics and Statics. Molecules 2023, 28, 7413. https://doi.org/10.3390/molecules28217413
Lach J, Okoniewska E. Adsorption of Chromium and Nickel Ions on Commercial Activated Carbon—An Analysis of Adsorption Kinetics and Statics. Molecules. 2023; 28(21):7413. https://doi.org/10.3390/molecules28217413
Chicago/Turabian StyleLach, Joanna, and Ewa Okoniewska. 2023. "Adsorption of Chromium and Nickel Ions on Commercial Activated Carbon—An Analysis of Adsorption Kinetics and Statics" Molecules 28, no. 21: 7413. https://doi.org/10.3390/molecules28217413
APA StyleLach, J., & Okoniewska, E. (2023). Adsorption of Chromium and Nickel Ions on Commercial Activated Carbon—An Analysis of Adsorption Kinetics and Statics. Molecules, 28(21), 7413. https://doi.org/10.3390/molecules28217413