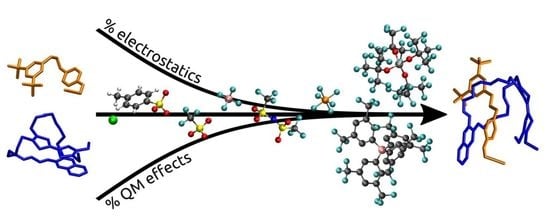
The Interplay of Weakly Coordinating Anions and the Mechanical Bond: A Systematic Study of the Explicit Influence of Counterions on the Properties of (Pseudo)rotaxanes
Abstract
:1. Introduction
2. Results
2.1. Pseudorotaxane Formation in ITC and NMR Experiments
2.2. Pseudorotaxane Formation In-Silico
2.3. Inter-Component Interactions in Pseudorotaxanes and Rotaxanes
3. Materials and Methods
3.1. Syntheses
3.2. ITC Experiments of MCAs and WCAs (BF, NTf, pf)
3.3. NMR Investigations of SCAs (BF, OTf)
3.4. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seppelt, K. Noncoordinating Anions, II. Angew. Chem. Int. Ed. 1993, 32, 1025–1027. [Google Scholar] [CrossRef]
- Gao, F.; Zhu, F.F.; Wang, X.Y.; Xu, Y.; Wang, X.P.; Zuo, J.L. Stabilizing Radical Cation and Dication of a Tetrathiafulvalene Derivative by a Weakly Coordinating Anion. Inorg. Chem. 2014, 53, 5321–5327. [Google Scholar] [CrossRef] [PubMed]
- Scholz, F.; Himmel, D.; Heinemann, F.W.; Schleyer, P.v.R.; Meyer, K.; Krossing, I. Crystal Structure Determination of the Nonclassical 2-Norbornyl Cation. Science 2013, 341, 62–64. [Google Scholar] [CrossRef] [PubMed]
- Krossing, I. Weakly Coordinating Anions: Fluorinated Alkoxyaluminates. In Comprehensive Inorganic Chemistry II; Elsevier: Amsterdam, The Netherlands, 2013; pp. 681–705. [Google Scholar] [CrossRef]
- Strauss, S.H. The search for larger and more weakly coordinating anions. Chem. Rev. 1993, 93, 927–942. [Google Scholar] [CrossRef]
- Riddlestone, I.M.; Kraft, A.; Schaefer, J.; Krossing, I. Taming the Cationic Beast: Novel Developments in the Synthesis and Application of Weakly Coordinating Anions. Angew. Chem. Int. Ed. 2018, 57, 13982–14024. [Google Scholar] [CrossRef] [PubMed]
- Krossing, I.; Raabe, I. Noncoordinating Anions—Fact or Fiction? A Survey of Likely Candidates. Angew. Chem. Int. Ed. 2004, 43, 2066–2090. [Google Scholar] [CrossRef]
- De, C.; Mitra, R.; List, B. Design and Synthesis of Enantiopure Tetrakis(pentafluorophenyl) Borate Analogues for Asymmetric Counteranion Directed Catalysis. Synlett 2017, 28, 2435–2438. [Google Scholar] [CrossRef] [Green Version]
- Levason, W.; Pugh, D.; Reid, G. Imidazolium-based ionic liquids with large weakly coordinating anions. New J. Chem. 2017, 41, 1677–1686. [Google Scholar] [CrossRef] [Green Version]
- Raabe, I.; Wagner, K.; Guttsche, K.; Wang, M.; Grätzel, M.; Santiso-Quiñones, G.; Krossing, I. Tetraalkylammonium Salts of Weakly Coordinating Aluminates: Ionic Liquids, Materials for Electrochemical Applications and Useful Compounds for Anion Investigation. Chem. Eur. J. 2009, 15, 1966–1976. [Google Scholar] [CrossRef]
- Tiessen, N.; Neumann, B.; Stammler, H.; Hoge, B. Synthesis and Characterization of Tetrakis(pentafluoroethyl)aluminate. Chem. Eur. J. 2020, 26, 13611–13614. [Google Scholar] [CrossRef]
- Riddlestone, I.M.; Keller, S.; Kirschenmann, F.; Schorpp, M.; Krossing, I. Towards Weakly Coordinating Anions with the Extremely Electron Withdrawing Perfluoropyridinoxy Ligand –OC5F4N. Eur. J. Inorg. Chem. 2019, 2019, 59–67. [Google Scholar] [CrossRef]
- Hoffmann, K.F.; Wiesner, A.; Subat, N.; Steinhauer, S.; Riedel, S. Salts of the Weakly Coordinating Anion [Al(OTeF5)4]- Containing Reactive Counterions. Z. Anorg. Allg. Chem. 2018, 644, 1344–1348. [Google Scholar] [CrossRef]
- Press, L.P.; McCulloch, B.J.; Gu, W.; Chen, C.H.; Foxman, B.M.; Ozerov, O.V. Triflyloxy-substituted carboranes as useful weakly coordinating anions. Chem. Commun. 2015, 51, 14034–14037. [Google Scholar] [CrossRef] [PubMed]
- Jenne, C.; Wegener, B. Silver Salts of the Weakly Coordinating Anion [Me3NB12Cl11]-. Z. Anorg. Allg. Chem. 2018, 644, 1123–1132. [Google Scholar] [CrossRef]
- Smidt, S.P.; Zimmermann, N.; Studer, M.; Pfaltz, A. Enantioselective Hydrogenation of Alkenes with Iridium–PHOX Catalysts: A Kinetic Study of Anion Effects. Chem. Eur. J. 2004, 10, 4685–4693. [Google Scholar] [CrossRef]
- Antoniotti, S.; Dalla, V.; Duñach, E. Metal Triflimidates: Better than Metal Triflates as Catalysts in Organic Synthesis-The Effect of a Highly Delocalized Counteranion. Angew. Chem. Int. Ed. 2010, 49, 7860–7888. [Google Scholar] [CrossRef]
- Si, G.; Tan, C.; Chen, M.; Chen, C. A Cocatalyst Strategy to Enhance Ruthenium-Mediated Metathesis Reactivity towards Electron-Deficient Substrates. Angew. Chem. Int. Ed. 2022, 61, e202203796. [Google Scholar] [CrossRef]
- Schröder, H.V.; Schalley, C.A. Tetrathiafulvalene—A redox-switchable building block to control motion in mechanically interlocked molecules. Beilstein J. Org. Chem. 2018, 14, 2163–2185. [Google Scholar] [CrossRef]
- Schenk, C.; Henke, F.; Santiso-Quiñones, G.; Krossing, I.; Schnepf, A. [Si(SiMe3)3]6Ge18M (M = Cu, Ag, Au): Metalloid cluster compounds as unusual building blocks for a supramolecular chemistry. Dalton Trans. 2008, 4436–4441. [Google Scholar] [CrossRef]
- Schmidbaur, H.; Schier, A. π-Complexation of Post-Transition Metals by Neutral Aromatic Hydrocarbons: The Road from Observations in the 19th Century to New Aspects of Supramolecular Chemistry. Organometallics 2008, 27, 2361–2395. [Google Scholar] [CrossRef]
- Barrière, F.; Geiger, W.E. Use of Weakly Coordinating Anions to Develop an Integrated Approach to the Tuning of ΔE 1/2 Values by Medium Effects. J. Am. Chem. Soc. 2006, 128, 3980–3989. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; McGonigal, P.R.; Schneebeli, S.T.; Li, H.; Vermeulen, N.A.; Ke, C.; Stoddart, J.F. An artificial molecular pump. Nat. Nanotechnol. 2015, 10, 547–553. [Google Scholar] [CrossRef] [PubMed]
- Schröder, H.V.; Mekic, A.; Hupatz, H.; Sobottka, S.; Witte, F.; Urner, L.H.; Gaedke, M.; Pagel, K.; Sarkar, B.; Paulus, B.; et al. Switchable synchronisation of pirouetting motions in a redox-active [3]rotaxane. Nanoscale 2018, 10, 21425–21433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Sun, R.; Zheng, R.; Huang, Y. Anions-responsive supramolecular gels: A review. Mater. Des. 2021, 205, 109759. [Google Scholar] [CrossRef]
- Wang, X.Q.; Wang, W.; Li, W.J.; Chen, L.J.; Yao, R.; Yin, G.Q.; Wang, Y.X.; Zhang, Y.; Huang, J.; Tan, H.; et al. Dual stimuli-responsive rotaxane-branched dendrimers with reversible dimension modulation. Nat. Commun. 2018, 9, 3190. [Google Scholar] [CrossRef] [PubMed]
- Evans, N.H.; Beer, P.D. Advances in Anion Supramolecular Chemistry: From Recognition to Chemical Applications. Angew. Chem. Int. Ed. 2014, 53, 11716–11754. [Google Scholar] [CrossRef] [Green Version]
- Cera, L.; Chiappisi, L.; Böttcher, C.; Schulz, A.; Schoder, S.; Gradzielski, M.; Schalley, C.A. PolyWhips: Directional Particle Transport by Gradient-Directed Growth and Stiffening of Supramolecular Assemblies. Adv. Mater. 2017, 29, 1604430. [Google Scholar] [CrossRef]
- Maynard, J.R.J.; Galmés, B.; Stergiou, A.D.; Symes, M.D.; Frontera, A.; Goldup, S.M. Anion–π Catalysis Enabled by the Mechanical Bond. Angew. Chem. Int. Ed. 2022, 61. [Google Scholar] [CrossRef]
- Hein, R.; Beer, P.D.; Davis, J.J. Electrochemical Anion Sensing: Supramolecular Approaches. Chem. Rev. 2020, 120, 1888–1935. [Google Scholar] [CrossRef]
- Langton, M.J.; Beer, P.D. Rotaxane and Catenane Host Structures for Sensing Charged Guest Species. Acc. Chem. Res. 2014, 47, 1935–1949. [Google Scholar] [CrossRef]
- Caballero, A.; Zapata, F.; Beer, P.D. Interlocked host molecules for anion recognition and sensing. Coord. Chem. Rev. 2013, 257, 2434–2455. [Google Scholar] [CrossRef]
- Amano, S.; Fielden, S.D.P.; Leigh, D.A. A catalysis-driven artificial molecular pump. Nature 2021, 594, 529–534. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Qiu, Y.; Liu, W.G.; Chen, H.; Shen, D.; Song, B.; Cai, K.; Wu, H.; Jiao, Y.; Feng, Y.; et al. An electric molecular motor. Nature 2023, 613, 280–286. [Google Scholar] [CrossRef]
- Farràs, P.; Escudero-Adán, E.C.; Viñas, C.; Teixidor, F. Controlling the Pirouetting Motion in Rotaxanes by Counterion Exchange. Inorg. Chem. 2014, 53, 8654–8661. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements ( Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef] [PubMed]
- Kitaura, K.; Ikeo, E.; Asada, T.; Nakano, T.; Uebayasi, M. Fragment molecular orbital method: An approximate computational method for large molecules. Chem. Phys. Lett. 1999, 313, 701–706. [Google Scholar] [CrossRef]
- Fedorov, D.G.; Kitaura, K. Pair interaction energy decomposition analysis. J. Comput. Chem. 2007, 28, 222–237. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.W.; Gibson, H.W. Ion Pairing and Host-Guest Complexation in Low Dielectric Constant Solvents. J. Am. Chem. Soc. 2003, 125, 7001–7004. [Google Scholar] [CrossRef]
- Gibson, H.W.; Jones, J.W.; Zakharov, L.N.; Rheingold, A.L.; Slebodnick, C. Complexation Equilibria Involving Salts in Non-Aqueous Solvents: Ion Pairing and Activity Considerations. Chem. Eur. J. 2011, 17, 3192–3206. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef] [PubMed]
- Hupatz, H.; Gaedke, M.; Schröder, H.V.; Beerhues, J.; Valkonen, A.; Klautzsch, F.; Müller, S.; Witte, F.; Rissanen, K.; Sarkar, B.; et al. Thermodynamic and electrochemical study of tailor-made crown ethers for redox-switchable (pseudo)rotaxanes. Beilstein J. Org. Chem. 2020, 16, 2576–2588. [Google Scholar] [CrossRef] [PubMed]
- Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325–340. [Google Scholar] [CrossRef]
- Morokuma, K. Molecular Orbital Studies of Hydrogen Bonds. III. C=O···H–O Hydrogen Bond in H2 CO···H2O and H2CO···2H2O. J. Chem. Phys. 1971, 55, 1236–1244. [Google Scholar] [CrossRef]
- Raghavachari, K.; Saha, A. Accurate Composite and Fragment-Based Quantum Chemical Models for Large Molecules. Chem. Rev. 2015, 115, 5643–5677. [Google Scholar] [CrossRef]
- Bannwarth, C.; Caldeweyher, E.; Ehlert, S.; Hansen, A.; Pracht, P.; Seibert, J.; Spicher, S.; Grimme, S. Extended tight-binding quantum chemistry methods. WIREs Comput. Mol. Sci. 2021, 11, e1493. [Google Scholar] [CrossRef]
- Sure, R.; Brandenburg, J.G.; Grimme, S. Small Atomic Orbital Basis Set First-Principles Quantum Chemical Methods for Large Molecular and Periodic Systems: A Critical Analysis of Error Sources. ChemistryOpen 2016, 5, 94–109. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for Mixing Exact Exchange with Density Functional Approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Sure, R.; Grimme, S. Comprehensive Benchmark of Association (Free) Energies of Realistic Host–Guest Complexes. J. Chem. Theory Comput. 2015, 11, 3785–3801. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory. Chem. Eur. J. 2012, 18, 9955–9964. [Google Scholar] [CrossRef]
- Spicher, S.; Grimme, S. Single-Point Hessian Calculations for Improved Vibrational Frequencies and Rigid-Rotor-Harmonic-Oscillator Thermodynamics. J. Chem. Theory Comput. 2021, 17, 1701–1714. [Google Scholar] [CrossRef]
- Eckert, F.; Klamt, A. Fast solvent screening via quantum chemistry: COSMO-RS approach. AIChE J. 2002, 48, 369–385. [Google Scholar] [CrossRef] [Green Version]
- Young Lee, G.; Bay, K.L.; Houk, K.N. Evaluation of DFT Methods and Implicit Solvation Models for Anion-Binding Host-Guest Systems. Helv. Chim. Acta 2019, 102, e1900032. [Google Scholar] [CrossRef]
- Ehrlich, S.; Moellmann, J.; Grimme, S. Dispersion-Corrected Density Functional Theory for Aromatic Interactions in Complex Systems. Acc. Chem. Res. 2013, 46, 916–926. [Google Scholar] [CrossRef]
- Witte, F.; Rietsch, P.; Sinha, S.; Krappe, A.; Joswig, J.O.; Götze, J.P.; Nirmalananthan-Budau, N.; Resch-Genger, U.; Eigler, S.; Paulus, B. Fluorescence Quenching in J-Aggregates through the Formation of Unusual Metastable Dimers. J. Phys. Chem. B 2021, 125, 4438–4446. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Schröder, H.V.; Sobottka, S.; Nößler, M.; Hupatz, H.; Gaedke, M.; Sarkar, B.; Schalley, C.A. Impact of mechanical bonding on the redox-switching of tetrathiafulvalene in crown ether–ammonium [2]rotaxanes. Chem. Sci. 2017, 8, 6300–6306. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.J.; Zhang, H.Y.; Wang, H.; Liu, Y. A Twin-Axial Hetero[7]rotaxane. Angew. Chem. Int. Ed. 2011, 50, 10834–10838. [Google Scholar] [CrossRef]
- Pracht, P.; Bohle, F.; Grimme, S. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [Green Version]
- Ehlert, S.; Stahn, M.; Spicher, S.; Grimme, S. Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods. J. Chem. Theory Comput. 2021, 17, 4250–4261. [Google Scholar] [CrossRef]
- Grimme, S.; Brandenburg, J.G.; Bannwarth, C.; Hansen, A. Consistent structures and interactions by density functional theory with small atomic orbital basis sets. J. Chem. Phys. 2015, 143, 054107. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.; Hansen, A.; Grimme, S. Best-Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. Int. Ed. 2022, 61, e202205735. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic Structure Calculations on Workstation Computers: The Program System Turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comp. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- COSMOtherm Program Suite COSMOlogic GmbH & Co KG. Available online: http://www.cosmologic.de (accessed on 29 March 2023).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]






| SCAs | MCAs | WCAs | ||||||
|---|---|---|---|---|---|---|---|---|
| X | Cl | OTs | OTf | BF | NTf | PF | BArF | pf |
| 1 | — 2 | 1 | 3 | 3 | ||||
| A1@TTFC8 | A1@TTFC8 | A1@TTFC8 | |
|---|---|---|---|
| 0.042 | 0.067 | 0.149 | |
| 0.058 | 0.051 | 0.043 |
| A1@TTFC8 | 375.8 | |||
| A1@TTFC8 | 451.9 |
| X | Cl | OTs | OTf | BF | NTf | PF | BArF | pf |
|---|---|---|---|---|---|---|---|---|
| (A1-X) | 4.0 | 19.9 | 26.8 | |||||
| (A1-X) | 0.82 | 0.70 | 0.73 | 0.80 | 0.69 | 0.75 | 0.47 | 0.55 |
| (A1@TTFC8) | 0.8 | |||||||
| (A1@TTFC8) | 0.37 | 0.38 | 0.38 | 0.39 | 0.39 | 0.38 | 0.40 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witte, J.F.; Wasternack, J.; Wei, S.; Schalley, C.A.; Paulus, B. The Interplay of Weakly Coordinating Anions and the Mechanical Bond: A Systematic Study of the Explicit Influence of Counterions on the Properties of (Pseudo)rotaxanes. Molecules 2023, 28, 3077. https://doi.org/10.3390/molecules28073077
Witte JF, Wasternack J, Wei S, Schalley CA, Paulus B. The Interplay of Weakly Coordinating Anions and the Mechanical Bond: A Systematic Study of the Explicit Influence of Counterions on the Properties of (Pseudo)rotaxanes. Molecules. 2023; 28(7):3077. https://doi.org/10.3390/molecules28073077
Chicago/Turabian StyleWitte, J. Felix, Janos Wasternack, Shenquan Wei, Christoph A. Schalley, and Beate Paulus. 2023. "The Interplay of Weakly Coordinating Anions and the Mechanical Bond: A Systematic Study of the Explicit Influence of Counterions on the Properties of (Pseudo)rotaxanes" Molecules 28, no. 7: 3077. https://doi.org/10.3390/molecules28073077
APA StyleWitte, J. F., Wasternack, J., Wei, S., Schalley, C. A., & Paulus, B. (2023). The Interplay of Weakly Coordinating Anions and the Mechanical Bond: A Systematic Study of the Explicit Influence of Counterions on the Properties of (Pseudo)rotaxanes. Molecules, 28(7), 3077. https://doi.org/10.3390/molecules28073077