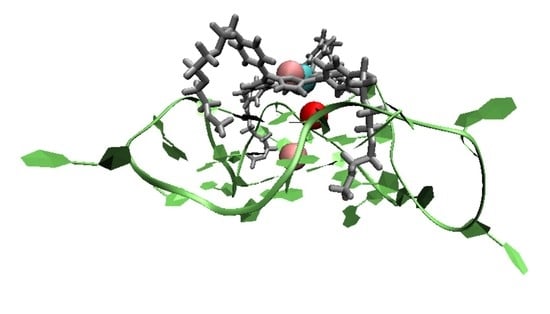
Towards Computational Modeling of Ligand Binding to the ILPR G-Quadruplex
Abstract
:1. Introduction

2. Results and Discussions
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neidle, S. Quadruplex nucleic acids as targets for anticancer therapeutics. Nat. Rev. Chem. 2017, 1, 41. [Google Scholar] [CrossRef]
- Wong, H.; Payet, L.; Huppert, J. Function and Targeting of G-Quadruplexes. Curr. Opin. Mol. Ther. 2009, 11, 146–155. [Google Scholar] [PubMed]
- Bochman, M.L.; Paeschke, K.; Zakian, V.A. DNA secondary structures: Stability and function of G-quadruplex structures. Nat. Rev. Genet. 2012, 13, 770–780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varshney, D.; Spiegel, J.; Zyner, K.; Tannahill, D.; Balasubramanian, S. The regulation and functions of DNA and RNA G-quadruplexes. Nat. Rev. Mol. Cell Biol. 2020, 21, 459–474. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Hurley, L.H. The Importance of Negative Superhelicity in Inducing the Formation of G-Quadruplex and i-Motif Structures in the c-Myc Promoter: Implications for Drug Targeting and Control of Gene Expression. J. Med. Chem. 2009, 52, 2863–2874. [Google Scholar] [CrossRef] [Green Version]
- Keith, W.N.; Evans, T.R.J.; Glasspool, R.M. Telomerase and cancer: Time to move from a promising target to a clinical reality. J. Pathol. 2001, 195, 404–414. [Google Scholar] [CrossRef] [PubMed]
- Huppert, J.L.; Balasubramanian, S. G-quadruplexes in promoters throughout the human genome. Nucleic Acids Res. 2006, 35, 406–413. [Google Scholar] [CrossRef] [Green Version]
- Spiegel, J.; Cuesta, S.M.; Adhikari, S.; Hänsel-Hertsch, R.; Tannahill, D.; Balasubramanian, S. G-quadruplexes are transcription factor binding hubs in human chromatin. Genome Biol. 2021, 22, 1–15. [Google Scholar] [CrossRef]
- Tian, T.; Chen, Y.-Q.; Wang, S.-R.; Zhou, X. G-Quadruplex: A Regulator of Gene Expression and Its Chemical Targeting. Chem 2018, 4, 1314–1344. [Google Scholar] [CrossRef] [Green Version]
- Fedeles, B.I. G-quadruplex–forming promoter sequences enable transcriptional activation in response to oxidative stress. Proc. Natl. Acad. Sci. USA 2017, 114, 2788–2790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lew, A.; Rutter, W.J.; Kennedy, G.C. Unusual DNA structure of the diabetes susceptibility locus IDDM2 and its effect on transcription by the insulin promoter factor Pur-1/MAZ. Proc. Natl. Acad. Sci. USA 2000, 97, 12508–12512. [Google Scholar] [CrossRef] [Green Version]
- Hammond-Kosack, M.C.U.; Dobrinski, B.; Lurz, R.; Docherty, K.; Kilpatrick, M.W. The human insulin gene linked polymorphic region exhibits an altered DNA structure. Nucleic Acids Res. 1992, 20, 231–236. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, G.C.; Rutter, W.J. Pur-1, a zinc-finger protein that binds to purine-rich sequences, transactivates an insulin promoter in heterologous cells. Proc. Natl. Acad. Sci. USA 1992, 89, 11498–11502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bell, G.I.; Karam, J.H.; Rutter, W.J. Polymorphic DNA region adjacent to the 5′ end of the human insulin gene. Proc. Natl. Acad. Sci. USA 1981, 78, 5759–5763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Connor, A.C.; Frederick, K.A.; Morgan, E.J.; McGown, L.B. Insulin Capture by an Insulin-Linked Polymorphic Region G-Quadruplex DNA Oligonucleotide. J. Am. Chem. Soc. 2006, 128, 4986–4991. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schonhoft, J.D.; Das, A.; Achamyeleh, F.; Samdani, S.; Sewell, A.; Mao, H.; Basu, S. ILPR repeats adopt diverse G-quadruplex conformations that determine insulin binding. Biopolymers 2009, 93, 21–31. [Google Scholar] [CrossRef]
- Yu, Z.; Schonhoft, J.D.; Dhakal, S.; Bajracharya, R.; Hegde, R.; Basu, S.; Mao, H. ILPR G-Quadruplexes Formed in Seconds Demonstrate High Mechanical Stabilities. J. Am. Chem. Soc. 2009, 131, 1876–1882. [Google Scholar] [CrossRef]
- Liu, H.-Y.; Zhao, Q.; Zhang, T.-P.; Wu, Y.; Xiong, Y.-X.; Wang, S.-K.; Ge, Y.-L.; He, J.-H.; Lv, P.; Ou, T.-M.; et al. Conformation Selective Antibody Enables Genome Profiling and Leads to Discovery of Parallel G-Quadruplex in Human Telomeres. Cell Chem. Biol. 2016, 23, 1261–1270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moye, A.L.; Porter, K.C.; Cohen, S.B.; Phan, T.; Zyner, K.G.; Sasaki, N.; Lovrecz, G.O.; Beck, J.L.; Bryan, T.M. Telomeric G-quadruplexes are a substrate and site of localization for human telomerase. Nat. Commun. 2015, 6, 7643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seenisamy, J.; Rezler, E.M.; Powell, T.J.; Tye, D.; Gokhale, V.; Joshi, C.S.; Siddiqui-Jain, A.; Hurley, L.H. The Dynamic Character of the G-Quadruplex Element in the c-MYC Promoter and Modification by TMPyP4. J. Am. Chem. Soc. 2004, 126, 8702–8709. [Google Scholar] [CrossRef] [PubMed]
- Martino, L.; Pagano, B.; Fotticchia, I.; Neidle, S.; Giancola, C. Shedding Light on the Interaction between TMPyP4 and Human Telomeric Quadruplexes. J. Phys. Chem. B 2009, 113, 14779–14786. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Guang, T.; Ye, X. Sedimentation velocity analysis of TMPyP4-induced dimer formation of human telomeric G-quadruplex. RSC Adv. 2017, 7, 55098–55105. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Bansal, M.; Bhattacharya, S. Ligand 5,10,15,20-Tetra(N-methyl-4-pyridyl)porphine (TMPyP4) Prefers the Parallel Propeller-Type Human Telomeric G-Quadruplex DNA over Its Other Polymorphs. J. Phys. Chem. B 2014, 119, 5–14. [Google Scholar] [CrossRef]
- Huang, X.-X.; Zhu, L.-N.; Wu, B.; Huo, Y.-F.; Duan, N.-N.; Kong, D.-M. Two cationic porphyrin isomers showing different multimeric G-quadruplex recognition specificity against monomeric G-quadruplexes. Nucleic Acids Res. 2014, 42, 8719–8731. [Google Scholar] [CrossRef] [Green Version]
- Laguerre, A.; Chang, Y.; Pirrotta, M.; Desbois, N.; Gros, C.P.; Lesniewska, E.; Monchaud, D. Surface-promoted aggregation of amphiphilic quadruplex ligands drives their selectivity for alternative DNA structures. Org. Biomol. Chem. 2015, 13, 7034–7039. [Google Scholar] [CrossRef] [PubMed]
- Diabate, P.D.; Laguerre, A.; Pirrotta, M.; Desbois, N.; Boudon, J.; Gros, C.P.; Monchaud, D. DNA structure-specific sensitization of a metalloporphyrin leads to an efficient in vitro quadruplex detection molecular tool. New J. Chem. 2016, 40, 5683–5689. [Google Scholar] [CrossRef]
- Myszka, D.G. Survey of the 1998 Optical Biosensor Literature. J. Mol. Recognit. 1999, 12, 390–408. [Google Scholar] [CrossRef]
- Dutta, A.K.; Rösgen, J.; Rajarathnam, K. Using Isothermal Titration Calorimetry to Determine Thermodynamic Parameters of Protein–Glycosaminoglycan Interactions. Methods Mol. Biol. 2015, 1229, 315–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, N.; Wickstrom, L.; Cieplak, P.; Lin, C.; Yang, D. Resolving the Ligand-Binding Specificity in c-MYC G-Quadruplex DNA: Absolute Binding Free Energy Calculations and SPR Experiment. J. Phys. Chem. B 2017, 121, 10484–10497. [Google Scholar] [CrossRef]
- Moraca, F.; Amato, J.; Ortuso, F.; Artese, A.; Pagano, B.; Novellino, E.; Alcaro, S.; Parrinello, M.; Limongelli, V. Ligand binding to telomeric G-quadruplex DNA investigated by funnel-metadynamics simulations. Proc. Natl. Acad. Sci. USA 2017, 114, E2136–E2145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Hagan, M.P.; Haldar, S.; Morales, J.C.; Mulholland, A.J.; Galan, M.C. Enhanced sampling molecular dynamics simulations correctly predict the diverse activities of a series of stiff-stilbene G-quadruplex DNA ligands. Chem. Sci. 2020, 12, 1415–1426. [Google Scholar] [CrossRef]
- Freyer, M.W.; Buscaglia, R.; Kaplan, K.; Cashman, D.; Hurley, L.H.; Lewis, E.A. Biophysical Studies of the c-MYC NHE III1 Promoter: Model Quadruplex Interactions with a Cationic Porphyrin. Biophys. J. 2007, 92, 2007–2015. [Google Scholar] [CrossRef] [Green Version]
- Clovis, N.S.; Sen, S. G-Tetrad-Selective Ligand Binding Kinetics in G-Quadruplex DNA Probed with Fluorescence Correlation Spectroscopy. J. Phys. Chem. B 2022, 126, 6007–6015. [Google Scholar] [CrossRef]
- Shapiro, A.J.; Lakey, J.R.; Ryan, E.A.; Korbutt, G.S.; Toth, E.; Warnock, G.L.; Kneteman, N.M.; Rajotte, R.V. Islet Transplantation in Seven Patients with Type 1 Diabetes Mellitus Using a Glucocorticoid-Free Immunosuppressive Regimen. N. Engl. J. Med. 2000, 343, 230–238. [Google Scholar] [CrossRef] [PubMed]
- Pagliuca, F.W.; Millman, J.R.; Gürtler, M.; Segel, M.; Van Dervort, A.; Ryu, J.H.; Peterson, Q.P.; Greiner, D.; Melton, D.A. Generation of Functional Human Pancreatic β Cells In Vitro. Cell 2014, 159, 428–439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rezania, A.; Bruin, J.E.; Arora, P.; Rubin, A.; Batushansky, I.; Asadi, A.; O’Dwyer, S.; Quiskamp, N.; Mojibian, M.; Albrecht, T.; et al. Reversal of diabetes with insulin-producing cells derived in vitro from human pluripotent stem cells. Nat. Biotechnol. 2014, 32, 1121–1133. [Google Scholar] [CrossRef]
- Paritala, H.; Firestine, S.M. Characterization of Insulin Ilpr Sequences for Their Ability to Adopt a G-Quadruplex Structure. Nucleosides Nucleotides Nucleic Acids 2010, 29, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Hammond-Kosack, M.C.U.; Kilpatrick, M.W.; Docherty, K. The human insulin gene-linked polymorphic region adopts a G-quartet structure in chromatin assembled in vitro. J. Mol. Endocrinol. 1993, 10, 121–126. [Google Scholar] [CrossRef] [PubMed]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera?A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [Green Version]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef] [Green Version]
- Lindahl, E.; Hess, B.; Van Der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Model. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Perez, A.; Marchán, I.; Svozil, D.; Sponer, J.; Cheatham, T.E., III; Laughton, C.A.; Orozco, M. Refinement of the AMBER Force Field for Nucleic Acids: Improving the Description of α/γ Conformers. Biophys. J. 2007, 92, 3817–3829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haider, S.; Neidle, S. Molecular Modeling and Simulation of G-Quadruplexes and Quadruplex-Ligand Complexes. In G-Quadruplex DNA; Baumann, P., Ed.; Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2010; Volume 608, pp. 17–37. ISBN 978-1-58829-950-5. [Google Scholar]
- Galindo-Murillo, R.; Robertson, J.C.; Zgarbová, M.; Šponer, J.; Otyepka, M.; Jurečka, P.; Cheatham, T.E. Assessing the Current State of Amber Force Field Modifications for DNA. J. Chem. Theory Comput. 2016, 12, 4114–4127. [Google Scholar] [CrossRef] [PubMed]
- Ivani, I.; Dans, P.D.; Noy, A.; Pérez, A.; Faustino, I.; Hospital, A.; Walther, J.; Andrio, P.; Goñi, R.; Balaceanu, A.; et al. Parmbsc1: A refined force field for DNA simulations. Nat. Methods 2016, 13, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Hou, X.-M.; Fu, Y.-B.; Wu, W.-Q.; Wang, L.; Teng, F.-Y.; Xie, P.; Wang, P.-Y.; Xi, X.-G. Involvement of G-triplex and G-hairpin in the multi-pathway folding of human telomeric G-quadruplex. Nucleic Acids Res. 2017, 45, 11401–11412. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Wu, Q.; Wang, T.; Li, L.-P.; Zhao, X.; Chen, K.; Qian, J.; Yuan, L.; Xu, H.; Mei, W.-J. Selective stabilization of multiple promoter G-quadruplex DNA by using 2-phenyl-1H-imidazole-based tanshinone IIA derivatives and their potential suppressing function in the metastatic breast cancer. Bioorganic Chem. 2020, 106, 104433. [Google Scholar] [CrossRef] [PubMed]
- Pandith, A.; Nagarajachari, U.; Siddappa, R.K.G.; Lee, S.; Park, C.; Sannathammegowda, K.; Seo, Y.J. Loop-mediated fluorescent probes for selective discrimination of parallel and antiparallel G-Quadruplexes. Bioorg. Med. Chem. 2021, 35, 116077. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef] [PubMed]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pettitt, B.M.; Karplus, M. The potential of mean force surface for the alanine dipeptide in aqueous solution: A theoretical approach. Chem. Phys. Lett. 1985, 121, 194–201. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Engin, O.; Villa, A.; Sayar, M.; Hess, B. Driving Forces for Adsorption of Amphiphilic Peptides to the Air−Water Interface. J. Phys. Chem. B 2010, 114, 11093–11101. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]






| ILPR G4-Ligand Systems | (kcal·mol−1) | (kcal·mol−1) | (kcal·mol−1) | (kcal·mol−1) | (kcal·mol−1) |
|---|---|---|---|---|---|
| ILPR G4-TEGPy a | −15.42 (±0.53) | −0.01 (±0.0006) | 9.54 (±0.0) | −5.62 (±0.27) | −11.50 (±0.59) |
| ILPR G4-TMPyP4 a | −12.88 (±0.43) | −0.02(±0.0007) | 9.43 (±0.0) | −5.73 (±0.05) | −9.18 (±0.43) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Barrow, J.; van Mourik, T.; Bühl, M. Towards Computational Modeling of Ligand Binding to the ILPR G-Quadruplex. Molecules 2023, 28, 3447. https://doi.org/10.3390/molecules28083447
Zhang X, Barrow J, van Mourik T, Bühl M. Towards Computational Modeling of Ligand Binding to the ILPR G-Quadruplex. Molecules. 2023; 28(8):3447. https://doi.org/10.3390/molecules28083447
Chicago/Turabian StyleZhang, Xiaotong, John Barrow, Tanja van Mourik, and Michael Bühl. 2023. "Towards Computational Modeling of Ligand Binding to the ILPR G-Quadruplex" Molecules 28, no. 8: 3447. https://doi.org/10.3390/molecules28083447
APA StyleZhang, X., Barrow, J., van Mourik, T., & Bühl, M. (2023). Towards Computational Modeling of Ligand Binding to the ILPR G-Quadruplex. Molecules, 28(8), 3447. https://doi.org/10.3390/molecules28083447