Phosphorus Modification of Iron: Mechanistic Insights into Ammonia Synthesis on Fe2P Catalyst
Abstract
:1. Introduction
2. Results and Discussion
2.1. Optimized Adsorbates and Their Binding Energies
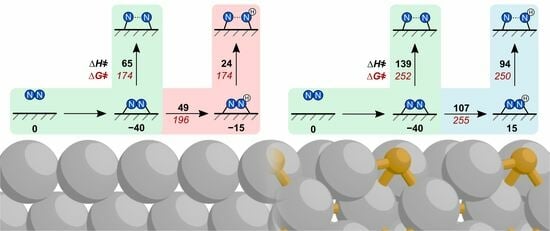
2.2. N–N Bond Activation Pathways on Fe(110)
2.3. N–N Bond Activation Pathways on Fe2P(001)
2.4. DFT-Predicted N–N Bond Cleavage Turnover Rate
3. Computational Methods
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- MacFarlane, D.R.; Cherepanov, P.V.; Choi, J.; Suryanto, B.H.R.; Hodgetts, R.Y.; Bakker, J.M.; Ferrero Vallana, F.M.; Simonov, A.N. A Roadmap to the Ammonia Economy. Joule 2020, 4, 1186–1205. [Google Scholar] [CrossRef]
- Smil, V. Enriching the Earth: Fritz Haber, Carl Bosch, and the Transformation of World Food Production; MIT Press: Cambridge, MA, USA, 2004; ISBN 0262693135. [Google Scholar]
- Pfromm, P.H. Towards Sustainable Agriculture: Fossil-Free Ammonia. J. Renew. Sustain. Energy 2017, 9, 034702. [Google Scholar] [CrossRef]
- Boudart, M. Kinetics and Mechanism of Ammonia Synthesis. Catal. Rev. 1981, 23, 1–15. [Google Scholar] [CrossRef]
- Honkala, K.; Hellman, A.; Remediakis, I.N.; Logadottir, A.; Carlsson, A.; Dahl, S.; Christensen, C.H.; Nørskov, J.K. Ammonia Synthesis from First-Principles Calculations. Science 2005, 307, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Schlögl, R. Catalytic Synthesis of Ammonia—A “Never-Ending Story”? Angew. Chem. Int. Ed. 2003, 42, 2004–2008. [Google Scholar] [CrossRef] [PubMed]
- Ertl, G. Surface Science and Catalysis—Studies on the Mechanism of Ammonia Synthesis: The P. H. Emmett Award Address. Catal. Rev. 1980, 21, 201–223. [Google Scholar] [CrossRef]
- Logadóttir, Á.; Nørskov, J.K. Ammonia Synthesis over a Ru(0001) Surface Studied by Density Functional Calculations. J. Catal. 2003, 220, 273–279. [Google Scholar] [CrossRef]
- Vojvodic, A.; Medford, A.J.; Studt, F.; Abild-Pedersen, F.; Khan, T.S.; Bligaard, T.; Nørskov, J.K. Exploring the Limits: A Low-Pressure, Low-Temperature Haber-Bosch Process. Chem. Phys. Lett. 2014, 598, 108–112. [Google Scholar] [CrossRef]
- Logadottir, A.; Rod, T.H.; Nørskov, J.K.; Hammer, B.; Dahl, S.; Jacobsen, C.J.H. The Brønsted-Evans-Polanyi Relation and the Volcano Plot for Ammonia Synthesis over Transition Metal Catalysts. J. Catal. 2001, 197, 229–231. [Google Scholar] [CrossRef]
- Munter, T.R.; Bligaard, T.; Christensen, C.H.; Nørskov, J.K. BEP Relations for N2 Dissociation over Stepped Transition Metal and Alloy Surfaces. Phys. Chem. Chem. Phys. 2008, 10, 5202–5206. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T.; Hvolbæk, B.; Abild-Pedersen, F.; Chorkendorff, I.; Christensen, C.H. The Nature of the Active Site in Heterogeneous Metal Catalysis. Chem. Soc. Rev. 2008, 37, 2163–2171. [Google Scholar] [CrossRef] [PubMed]
- Medford, A.J.; Vojvodic, A.; Hummelshøj, J.S.; Voss, J.; Abild-Pedersen, F.; Studt, F.; Bligaard, T.; Nilsson, A.; Nørskov, J.K. From the Sabatier Principle to a Predictive Theory of Transition-Metal Heterogeneous Catalysis. J. Catal. 2015, 328, 36–42. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T.; Logadottir, A.; Bahn, S.; Hansen, L.B.; Bollinger, M.; Bengaard, H.; Hammer, B.; Sljivancanin, Z.; Mavrikakis, M.; et al. Universality in Heterogeneous Catalysis. J. Catal. 2002, 209, 275–278. [Google Scholar] [CrossRef]
- Jacobsen, C.J.H.; Dahl, S.; Clausen, B.G.S.; Bahn, S.; Logadottir, A.; Nørskov, J.K. Catalyst Design by Interpolation in the Periodic Table: Bimetallic Ammonia Synthesis Catalysts. J. Am. Chem. Soc. 2001, 123, 8404–8405. [Google Scholar] [CrossRef] [PubMed]
- Zeinalipour-Yazdi, C.D.; Hargreaves, J.S.J.; Catlow, C.R.A. Nitrogen Activation in a Mars–van Krevelen Mechanism for Ammonia Synthesis on Co3Mo3N. J. Phys. Chem. C 2015, 119, 28368–28376. [Google Scholar] [CrossRef]
- Jacobsen, C.J.H. Novel Class of Ammonia Synthesis Catalysts. Chem. Commun. 2000, 1057–1058. [Google Scholar] [CrossRef]
- Wang, P.; Chang, F.; Gao, W.; Guo, J.; Wu, G.; He, T.; Chen, P. Breaking Scaling Relations to Achieve Low-Temperature Ammonia Synthesis through LiH-Mediated Nitrogen Transfer and Hydrogenation. Nat. Chem. 2017, 9, 64–70. [Google Scholar] [CrossRef]
- Vojvodic, A.; Calle-Vallejo, F.; Guo, W.; Wang, S.; Toftelund, A.; Studt, F.; Martínez, J.I.; Shen, J.; Man, I.C.; Rossmeisl, J.; et al. On the Behavior of Brønsted-Evans-Polanyi Relations for Transition Metal Oxides. J. Chem. Phys. 2011, 134, 244509. [Google Scholar] [CrossRef]
- Somorjai, G.A.; Materer, N. Surface Structures in Ammonia Synthesis. Top. Catal. 1994, 1, 215–231. [Google Scholar] [CrossRef]
- Qian, J.; An, Q.; Fortunelli, A.; Nielsen, R.J.; Goddard, W.A. Reaction Mechanism and Kinetics for Ammonia Synthesis on the Fe(111) Surface. J. Am. Chem. Soc. 2018, 140, 6288–6297. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, T.; Zhang, H.; Li, X.; Shi, A.; Li, X.; Wang, Q.; Hu, G. Fe2P Nanoparticle-Decorated Porous Biochar for High-Efficiency Electrosynthesis of Ammonia from Toxic Nitrite. Surf. Interfaces 2023, 38, 102818. [Google Scholar] [CrossRef]
- Chouki, T.; Machreki, M.; Rutkowska, I.A.; Rytelewska, B.; Kulesza, P.J.; Tyuliev, G.; Harb, M.; Azofra, L.M.; Emin, S. Highly Active Iron Phosphide Catalysts for Selective Electrochemical Nitrate Reduction to Ammonia. J. Environ. Chem. Eng. 2023, 11, 109275. [Google Scholar] [CrossRef]
- Witzke, M.E.; Almithn, A.; Conrad, C.L.; Hibbitts, D.D.; Flaherty, D.W. Mechanisms and Active Sites for C–O Bond Rupture within 2-Methyltetrahydrofuran over Ni, Ni12P5, and Ni2P Catalysts. ACS Catal. 2018, 8, 7141–7157. [Google Scholar] [CrossRef]
- Almithn, A.; Alhulaybi, Z. A Mechanistic Study of Methanol Steam Reforming on Ni2P Catalyst. Catalysts 2022, 12, 1174. [Google Scholar] [CrossRef]
- Almithn, A.; Alghanim, S.N.; Mohammed, A.A.; Alghawinim, A.K.; Alomaireen, M.A.; Alhulaybi, Z.; Hossain, S.S. Methane Activation and Coupling Pathways on Ni2P Catalyst. Catalysts 2023, 13, 531. [Google Scholar] [CrossRef]
- Waldt, C.; Montalvo-Castro, H.; Almithn, A.; Loaiza-Orduz, Á.; Plaisance, C.; Hibbitts, D. Role of Phosphorous in Transition Metal Phosphides for Selective Hydrogenolysis of Hindered C–O Bonds. J. Catal. 2023, 421, 403–418. [Google Scholar] [CrossRef]
- Mortensen, J.J.; Hansen, L.B.; Hammer, B.; Nørskov, J.K. Nitrogen Adsorption and Dissociation on Fe(111). J. Catal. 1999, 182, 479–488. [Google Scholar] [CrossRef]
- Logadottir, A.; Nørskov, J.K. The Effect of Strain for N2 Dissociation on Fe Surfaces. Surf. Sci. 2001, 489, 135–143. [Google Scholar] [CrossRef]
- Wang, T.; Tian, X.; Yang, Y.; Li, Y.-W.; Wang, J.; Beller, M.; Jiao, H. Coverage-Dependent N2 Adsorption and Its Modification of Iron Surfaces Structures. J. Phys. Chem. C 2016, 120, 2846–2854. [Google Scholar] [CrossRef]
- Witzke, M.E.; Almithn, A.; Conrad, C.L.; Triezenberg, M.D.; Hibbitts, D.D.; Flaherty, D.W. In Situ Methods for Identifying Reactive Surface Intermediates during Hydrogenolysis Reactions: C–O Bond Cleavage on Nanoparticles of Nickel and Nickel Phosphides. J. Am. Chem. Soc. 2019, 141, 16671–16684. [Google Scholar] [CrossRef]
- Egeberg, R.C.; Dahl, S.; Logadottir, A.; Larsen, J.H.; Nùrskov, J.K.; Chorkendorff, I. N2 Dissociation on Fe(1 1 0) and Fe/Ru(0 0 0 1): What Is the Role of Steps? Surf. Sci. 2001, 491, 183–194. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kravchenko, P.; Plaisance, C.; Hibbitts, D. A New Computational Interface for Catalysis. ChemRxiv 2019. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Wilburn, D.R.; Bassett, W.A. Hydrostatic Compression of Iron and Related Compounds; an Overview. Am. Mineral. 1978, 63, 591–596. [Google Scholar]
- Koumina, A.; Bacmann, M.; Fruchart, D.; Soubeyroux, J.-L.; Wolfers, P.; Tobola, J.; Kaprzyk, S.; Niziol, S.; Mesnaoui, M.; Zach, R. Crystallographic and Magnetic Properties of Fe2P. Ann. Chim. Sci. Des Mater. 1998, 23, 177–180. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special Points for Brillouin-Zone Integrations”—A Reply. Phys. Rev. B 1977, 16, 1748–1749. [Google Scholar] [CrossRef]
- Henkelman, G.; Jónsson, H. Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
- Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions. In Proceedings of the Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
- Henkelman, G.; Jónsson, H. A Dimer Method for Finding Saddle Points on High Dimensional Potential Surfaces Using Only First Derivatives. J. Chem. Phys. 1999, 111, 7010–7022. [Google Scholar] [CrossRef]
- McQuarrie, D.A. Statistical Mechanics; University Science Books: Sausalito, CA, USA, 2000. [Google Scholar]








| Fe(110) | Fe2P(001) | |||
|---|---|---|---|---|
| Species | Adsorption Mode | ΔEads | Adsorption Mode | ΔEads |
| kJ mol−1 | kJ mol−1 | |||
| N2* | M1 | −33 | M1 | −47 |
| N* | M3 | −576 | M3 | −518 |
| NH* | M3 | −465 | M3 | −426 |
| NH2* | M2 | −263 | M2 | −258 |
| NH3* | M1 | −52 | M1 | −64 |
| H* | M3 | −272 | M3 | −256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almithn, A. Phosphorus Modification of Iron: Mechanistic Insights into Ammonia Synthesis on Fe2P Catalyst. Molecules 2024, 29, 1894. https://doi.org/10.3390/molecules29081894
Almithn A. Phosphorus Modification of Iron: Mechanistic Insights into Ammonia Synthesis on Fe2P Catalyst. Molecules. 2024; 29(8):1894. https://doi.org/10.3390/molecules29081894
Chicago/Turabian StyleAlmithn, Abdulrahman. 2024. "Phosphorus Modification of Iron: Mechanistic Insights into Ammonia Synthesis on Fe2P Catalyst" Molecules 29, no. 8: 1894. https://doi.org/10.3390/molecules29081894
APA StyleAlmithn, A. (2024). Phosphorus Modification of Iron: Mechanistic Insights into Ammonia Synthesis on Fe2P Catalyst. Molecules, 29(8), 1894. https://doi.org/10.3390/molecules29081894