The Study of Dynamic Potentials of Highly Excited Vibrational States of DCP: From Case Analysis to Comparative Study with HCP
Abstract
:1. Introduction
2. The Semi-Classical Hamiltonian of the DCP
3. The Dynamic Features of the Highly Excited Vibration States of DCP
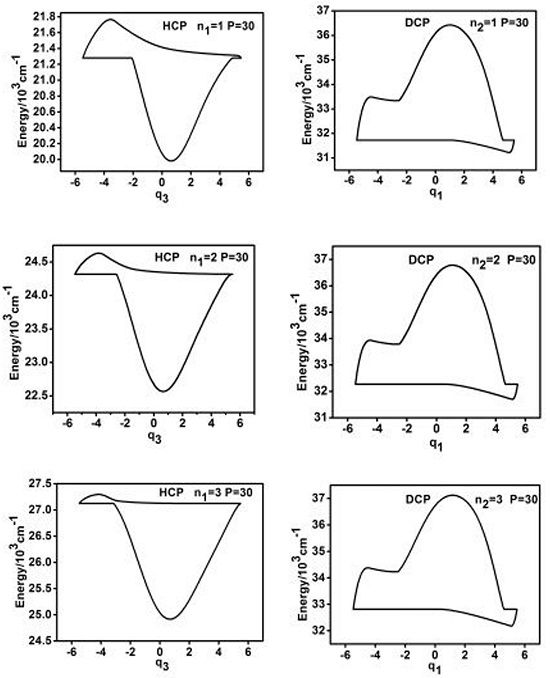
3.1. The Dynamic Potentials Corresponding Typical Polyad Number with Different Quantum Number
3.2. The Trajectories of Phase Space Study for the Energy Levels under Specific Polyad Number (P = 30)
3.3. Comparative Study between DCP and HCP with Dynamic Potential
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Peterson, K.A.; Skokov, S.; Bowman, J. A theoretical study of the vibrational energy spectrum of the HOCl/HClO system on an accurate ab initio potential energy surface. J. Chem. Phys. 1999, 111, 7446–7456. [Google Scholar] [CrossRef]
- Peterson, K.A. An accurate global ab initio potential energy surface for the X(1)A′ electronic state of HOBr. J. Chem. Phys. 2000, 113, 4598–4612. [Google Scholar] [CrossRef]
- Joyeux, M.; Sugny, D.; Lombardi, M.; Jost, R.; Schinke, R.; Skokov, S.; Bowman, J. Vibrational dynamics up to the dissociation threshold: A case study of two-dimensional HOCl. J. Chem. Phys. 2000, 113, 9610–9621. [Google Scholar] [CrossRef] [Green Version]
- Joyeux, M.; Grebenshchikov, S.Y.; Bredenbeck, J.; Schinke, R.; Farantos, S.C. Phase space geometry of multi-dimensional dynamic systems and reaction processes. In Geometric Structures of Phase Space in Multidimensional Chaos: Applications to Chemical Reaction Dynamics in Complex Systems, Volume 130; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Fang, C.; Wu, G.Z. Dynamic similarity in the highly excited vibrations of HCP and DCP: The dynamic potential approach. Comp. Theor. Chem. 2009, 910, 141–147. [Google Scholar]
- Wang, A.X.; Sun, L.F.; Fang, C.; Liu, Y.B. The study of dynamic potentials of highly excited vibrational states of HOBr. Int. J. Mol. Sci. 2013, 14, 5250–5263. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Wu, G.Z. Global dynamic analysis of vibrational manifolds of HOCl and HOBr under anharmonicity and Fermi resonance: the dynamic potential approach. Chin. Phys. B 2010, 19, 010509. [Google Scholar]
- Fang, C.; Wu, G.Z. Bending localization of nitrous oxide under anharmonicity and Fermi coupling: The dynamic potential approach. Chin. Phys. B 2010, 19, 110513. [Google Scholar]
- Biczysko, M.; Tarroni, R. Theoretical calculation of rovibronic energy levels and anharmonic resonances in the ground X (2)Pi state of HCP+ and DCP+. Phys. Chem. Chem. Phys. 2002, 4, 708–715. [Google Scholar] [CrossRef]
- Fang, C.; Wu, G.Z. Dynamic potential approach to dissociation of H–C bond in HCO highly excited vibration. Chin. Phys. B 2009, 18, 130–135. [Google Scholar]
- Kellman, M.E. Approximate constants of motion for vibrational-spectra of many-oscillator systems with multiple anharmonic resonances. J. Phys. Chem. 1990, 93, 6630–6635. [Google Scholar] [CrossRef]
- Wang, A.X.; Liu, Y.B.; Fang, C. The study of the dynamic potentials of highly excited vibrational states in HOCl molecular system. Acta Phys. Sin. 2012, 61, 053102. [Google Scholar]
- Zhang, W.M.; Feng, D.H.; Gilmore, R. Coherent states: Theory and some applications. Rev. Mod. Phys. 1990, 62, 867–927. [Google Scholar] [CrossRef]
- Weiss, J.; Hauschildt, J.; Grebenshchikov, S.Y.; Duren, R.; Schinke, R.; Koput, J.; Stamatiadis, S.; Farantos, S.C. Saddle-node bifurcations in the spectrum of HOCl. J. Chem. Phys. 2000, 112, 77–79. [Google Scholar] [CrossRef]







| Parameter Name | Parameter Values (cm−1) | Parameter Name | Parameter Values (cm−1) |
|---|---|---|---|
| 2494.0412 | y223 | 0.0482 | |
| 539.1611 | y233 | 0.2535 | |
| 1237.0955 | y333 | −0.2447 | |
| X11 | −24.0769 | z1111 | 0.0510 |
| X12 | −11.1041 | z1112 | 0.0806 |
| X13 | −4.6276 | z1222 | −0.0055 |
| X22 | −3.5142 | z1233 | 0.0280 |
| X23 | −2.2082 | z2222 | −0.0014 |
| X33 | −2.2082 | z2233 | −0.0067 |
| y111 | −0.8896 | z2333 | −0.0132 |
| y112 | −0.4928 | z3333 | 0.0092 |
| y113 | −0.5407 | k | 12.3422 |
| y122 | 0.2167 | λ1 | 0.5786 |
| y123 | −0.3655 | λ3 | 0.1212 |
| y133 | −0.2167 | μ11 | −0.2990 |
| y222 | 0.0884 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Fang, C.; Liu, Y. The Study of Dynamic Potentials of Highly Excited Vibrational States of DCP: From Case Analysis to Comparative Study with HCP. Int. J. Mol. Sci. 2016, 17, 1280. https://doi.org/10.3390/ijms17081280
Wang A, Fang C, Liu Y. The Study of Dynamic Potentials of Highly Excited Vibrational States of DCP: From Case Analysis to Comparative Study with HCP. International Journal of Molecular Sciences. 2016; 17(8):1280. https://doi.org/10.3390/ijms17081280
Chicago/Turabian StyleWang, Aixing, Chao Fang, and Yibao Liu. 2016. "The Study of Dynamic Potentials of Highly Excited Vibrational States of DCP: From Case Analysis to Comparative Study with HCP" International Journal of Molecular Sciences 17, no. 8: 1280. https://doi.org/10.3390/ijms17081280
APA StyleWang, A., Fang, C., & Liu, Y. (2016). The Study of Dynamic Potentials of Highly Excited Vibrational States of DCP: From Case Analysis to Comparative Study with HCP. International Journal of Molecular Sciences, 17(8), 1280. https://doi.org/10.3390/ijms17081280