Exploring the Structural Transformation Mechanism of Chinese and Thailand Silk Fibroin Fibers and Formic-Acid Fabricated Silk Films
Abstract
:1. Introduction
2. Results and Discussion
2.1. Dynamic Mechanical Analysis of the Degumming Silk Fiber
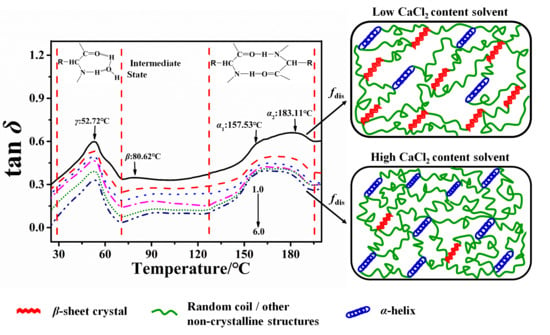
2.2. Structural Transformation of Chin and Thai Silk Protein Films
2.3. Stress-Strain Study of CSF and TSF
3. Materials and Methods
3.1. Materials and Preparation
3.2. Thermal and Mechanical Analyses
3.3. Fourier Transform Infrared Spectrometry
3.4. Thermogravimetric Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bhardwaj, N.; Singh, Y.P.; Devi, D.; Kandimalla, R.; Kotoky, J.; Manda, B.B. Potential of silk fibroin/chondrocyte constructs of muga silkworm Antheraea assamensis for cartilage tissue engineering. J. Mater. Chem. B 2016, 4, 3670–3684. [Google Scholar] [CrossRef]
- Yu, S.; Yang, W.; Chen, S.; Chen, M.; Liu, Y.; Shao, Z.; Chen, X. Floxuridine-loaded silk fibroin nanospheres. RSC Adv. 2014, 4, 18171–18177. [Google Scholar] [CrossRef]
- Hu, X.; Wang, X.; Rnjak, J.; Weiss, A.S.; Kaplan, D.L. Biomaterials derived from silk-tropoelastin protein systems. Biomaterials 2010, 31, 8121–8131. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Shmelev, K.; Sun, L. Regulation of Silk Material Structure by Temperature-Controlled Water Vapor Annealing. Biomacromolecules 2011, 12, 1686–1696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jao, D.; Xue, Y.; Medina, J.; Hu, X. Protein-Based Drug-Delivery Materials. Materials 2017, 10, 517. [Google Scholar] [CrossRef] [PubMed]
- Kambe, Y.; Murakoshi, A.; Urakawa, H.; Kimura, Y.; Yamaoka, T. Vascular induction and cell infiltration into peptide-modified bioactive silk fibroin hydrogels. J. Mater. Chem. B 2017, 5, 7557–7571. [Google Scholar] [CrossRef]
- Aytemiz, D.; Sakiyama, W.; Suzuki, Y.; Nakaizumi, N.; Tanaka, R.; Ogawa, Y.; Takagi, Y.; Nakazawa, Y.; Asakura, T. Small-diameter silk vascular grafts (3 mm diameter) with a double-raschel knitted silk tube coated with silk fibroin sponge. Adv. Healthc. Mater. 2013, 2, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Shahbazi, B.; Taghipour, M.; Rahmani, H.; Sadrjavadi, K.; Fattahi, A. Preparation and characterization of silk fibroin/oligochitosan nanoparticles for siRNA delivery. Colloids Surf. B 2015, 136, 867–877. [Google Scholar] [CrossRef] [PubMed]
- Tesfaye, M.; Patwa, R.; Kommadath, R.; Kotecha, P.; Katiyar, V. Silk nanocrystals stabilized melt extruded poly (lactic acid) nanocomposite films: Effect of recycling on thermal degradation kinetics and optimization studies. Thermochim. Acta 2016, 643, 41–52. [Google Scholar] [CrossRef]
- Yin, Z.; Wu, F.; Xing, T.; Yadavalli, V.K.; Kundu, S.C.; Lu, S. A silk fibroin hydrogel with reversible sol-gel transition. RSC Adv. 2017, 7, 24085–24096. [Google Scholar] [CrossRef]
- Hu, X.; Park, S.H.; Gil, E.S.; Xia, X.X.; Weiss, A.S.; Kaplan, D.L. The Influence of Elasticity and Surface Roughness on Myogenic and Osteogenic-Differentiation of Cells on Silk-Elastin Biomaterials. Biomaterials 2011, 32, 8979–8989. [Google Scholar] [CrossRef] [PubMed]
- Phillips, D.M.; Drummy, L.F.; Conrady, D.G.; Fox, D.M.; Naik, R.R.; Stone, M.O. Dissolution and Regeneration of Bombyx mori Silk Fibroin Using Ionic Liquids. J. Am. Chem. Soc. 2004, 126, 14350–14361. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Hu, X.; Wang, X.; Kluge, J.A.; Lu, S. Water-Insoluble Silk Films with Silk I Structure. Acta Biomater. 2010, 6, 1380–1387. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Chen, Y.; Min, S. Research on Cytotoxicity of Silk Fibroin Gel Materials Prepared with Polyepoxy Compound. J. Biomed. Eng. 2007, 24, 1309–1313. [Google Scholar]
- Crawford, D.M.; Escarsega, J.A. Dynamic mechanical analysis of novel polyurethane coating for military applications. Thermochim. Acta 2000, 357, 161–168. [Google Scholar] [CrossRef]
- Yin, B.; Hakkarainen, M. Core–shell nanoparticle–plasticizers for design of high-performance polymeric materials with improved stiffness and toughness. J. Mater. Chem. 2011, 21, 8670–8677. [Google Scholar] [CrossRef]
- Khandaker, M.S.K.; Dudek, D.M.; Beers, E.P.; Dillard, D.A.; Bevan, D.R. Molecular modeling of the elastomeric properties of repeating units and building blocks of resilin, a disordered elastic protein. J. Mech. Behav. Biomed. Mater. 2016, 61, 110–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahdi, E.M.; Tan, J.C. Dynamic molecular interactions between polyurethane and ZIF-8 in a polymer-MOF nanocomposite: Microstructural, thermo-mechanical and viscoelastic effects. Polymer 2016, 97, 31–43. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M.; Alothman, O.Y.; Paridah, M.T. A review on dynamic mechanical properties of natural fibre reinforced polymer composites. Constr. Build. Mater. 2016, 106, 149–159. [Google Scholar] [CrossRef]
- Nalyanya, K.M.; Migunde, O.P.; Ngumbu, R.G.; Onyuka, A.; Rop, R.K. Thermal and dynamic mechanical analysis of bovine hide. J. Therm. Anal. Calorim. 2016, 121, 1–8. [Google Scholar] [CrossRef]
- Guan, J.; Porter, D.; Vollrath, F. Thermally induced changes in dynamic mechanical properties of native silks. Biomacromolecules 2013, 14, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Guan, J.; Hawkins, N.; Porter, D.; Shao, Z. Understanding the variability of properties in Antheraea pernyi silk fibres. Soft Matter 2014, 10, 6321–6331. [Google Scholar] [CrossRef] [PubMed]
- Vollrath, F.; Porter, D. Spider silk as a model biomaterial. Appl. Phys. A 2006, 82, 205–212. [Google Scholar] [CrossRef]
- Porter, D.; Vollrath, F.; Shao, Z. Predicting the mechanical properties of spider silk as a nanostructured polymer. Eur. Phys. J. E 2005, 16, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Kawano, Y.; Wang, Y.; Palmer, R.; Aubuchon, A.; Steve, R. Stress-Strain Curves of Nafion Membranes in Acid and Salt Forms. Polímeros 2002, 12, 96–101. [Google Scholar] [CrossRef]
- Pyda, M.; Wunderlich, B. Reversing and nonreversing heat capacity of poly (lactic acid) in the glass transition region by TMDSC. Macromolecules 2005, 38, 10472–10479. [Google Scholar] [CrossRef]
- Sheng, S.J.; Hu, X.; Wang, F.; Ma, Q.Y.; Gu, M.F. Mechanical and thermal property characterization of poly-L-lactide (PLLA) scaffold developed using pressure-controllable green foaming technology. Mat. Sci. Eng. C.-Mater. 2015, 49, 612–622. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wolf, N.; Rocks, E.M.; Vuong, T.; Hu, X. Comparative studies of regenerated water-based Mori, Thai, Eri, Muga and Tussah silk fibroin films. J. Therm. Anal. Calorim. 2015, 122, 1069–1076. [Google Scholar] [CrossRef]
- Mazzi, S.; Zulker, E.; Buchicchio, J.; Anderson, B.; Hu, X. Comparative thermal analysis of Eri, Mori, Muga, and Tussar silk cocoons and fibroin fibers. J. Therm. Anal. Calorim. 2014, 116, 1337–1343. [Google Scholar] [CrossRef]
- Wang, F.; Yu, H.Y.; Gu, Z.G.; Si, L.; Liu, Q.C.; Hu, X. Impact of calcium chloride concentration on structure and thermal property of Thai silk fibroin films. J. Therm. Anal. Calorim. 2017, 130, 1–9. [Google Scholar] [CrossRef]
- Wang, F.; Chandler, P.; Oszust, R.; Sowell, E.; Graham, Z.; Ardito, W.; Hu, X. Thermal and structural analysis of silk–polyvinyl acetate blends. J. Therm. Anal. Calorim. 2017, 127, 923–929. [Google Scholar] [CrossRef]
- Hu, X.; Lu, Q.; Sun, L.; Cebe, P.; Wang, X.Q.; Zhang, X.H.; Kaplan, D.L. Biomaterials from Ultrasonication-Induced Silk Fibroin−Hyaluronic Acid Hydrogels. Biomacromolecules 2010, 11, 3178–3188. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Jiang, C.; Cheng, Q.; Zhang, J.; Guo, S. Accelerated aging test of hydrogenated nitrile butadiene rubber using the time-temperature-strain superposition principle. RSC Adv. 2015, 5, 90178–90183. [Google Scholar] [CrossRef]
- Butaud, P.; Placet, V.; Klesa, J.; Ouisse, M.; Foltête, E.; Gabrion, X. Investigations on the frequency and temperature effects on mechanical properties of a shape memory polymer (Veriflex). Mech. Mater. 2015, 8, 50–60. [Google Scholar] [CrossRef]
- Ardhyananta, H.; Kawauchi, T.; Ismail, H.; Takeichi, T. Effect of pendant group of polysiloxanes on the thermal and mechanical properties of polybenzoxazine hybrids. Polymer 2009, 25, 5959–5969. [Google Scholar] [CrossRef]
- Hu, X.; Kaplan, D.; Cebe, P. Effect of Water on Thermal Properties of Silk Fibroin. Thermochim. Acta 2007, 461, 137–144. [Google Scholar] [CrossRef]
- Motta, A.; Fambri, L.; Migliaresi, C. Regenerated silk fibroin films: Thermal and dynamic mechanical analysis. Chem. Phys. 2002, 203, 1658–1665. [Google Scholar] [CrossRef]
- Um, I.C.; Kim, T.H.; Kweon, H.Y.; Chang, S.K.; Park, Y.H. A comparative study on the dielectric and dynamic mechanical relaxation behavior of the regenerated silk fibroin films. Macromol. Res. 2009, 17, 785–790. [Google Scholar] [CrossRef]
- Born, M. Thermodynamics of crystals and melting. J. Chem. Phys. 1939, 7, 591–603. [Google Scholar] [CrossRef]
- Guan, J.; Wang, Y.; Mortimer, B.; Holland, C.; Shao, Z.; Porter, D.; Vollrath, F. Glass transitions in native silk fibres studied by dynamic mechanical thermal analysis. Soft Matter 2016, 12, 5926–5936. [Google Scholar] [CrossRef] [PubMed]
- Porter, D.; Vollrath, F. Water mobility denaturation and the glass transition in proteins. Biochim. Biophys. Acta 2012, 1824, 785–791. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Porter, D.; Vollrath, F. Silk cocoon (Bombyx mori): Multi-layer structure and mechanical properties. Acta Biomater. 2012, 8, 2620–2627. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Porter, D.; Chen, X.; Vollrath, F.; Shao, Z. Understanding the Mechanical Properties of Antheraea Pernyi Silk-From Primary Structure to Condensed Structure of the Protein. Adv. Funct. Mater. 2015, 21, 729–737. [Google Scholar] [CrossRef]
- Qin, G.; Hu, X.; Cebe, P.; Kaplan, D.L. Mechanism of resilin elasticity. Nat. Commun. 2012, 3, 1003–1013. [Google Scholar] [CrossRef] [PubMed]
- Roberts, D.R.T.; Holder, S.J. Mechanochromic systems for the detection of stress, strain and deformation in polymeric materials. J. Mater. Chem. 2011, 21, 8256–8268. [Google Scholar] [CrossRef]
- Hu, X.; Kaplan, D.; Cebe, P. Determining beta-sheet crystallinity in fibrous proteins by thermal analysis and infrared spectroscopy. Macromolecules 2006, 39, 6161–6170. [Google Scholar] [CrossRef]
- Yu, H.Y.; Wang, F.; Liu, Q.C.; Ma, Q.Y.; Gu, Z.G. Structure and Kinetics of Thermal Decomposition Mechanism of Novel Silk Fibroin Films. Acta Phys.-Chim. Sin. 2017, 33, 344–355. [Google Scholar]
- Sgreccia, E.; Chailan, G.F.; Khadhraoui, M.; Vona, M.L.D.; Knauth, P. Mechanical properties of proton-conducting sulfonated aromatic polymer membranes: Stress–strain tests and dynamical analysis. J. Power Sources 2010, 195, 7770–7775. [Google Scholar] [CrossRef] [Green Version]



| Sample | Water Content/% | Sample | Water Content/% |
|---|---|---|---|
| CRS | 9.70 | TRS | 7.26 |
| CSF-1.0 | 3.23 | TSF-1.0 | 1.26 |
| CSF-1.5 | 2.97 | TSF-1.5 | 1.04 |
| CSF-2.0 | 2.05 | TSF-2.0 | 1.10 |
| CSF-3.0 | 1.79 | TSF-3.0 | 1.20 |
| CSF-4.0 | 1.35 | TSF-4.0 | 0.52 |
| CSF-6.0 | 1.16 | TSF-6.0 | 0.51 |
| Sample | CRS/TRS | |||
|---|---|---|---|---|
| Attribution | γ | β | α | αc |
| E′/MPa | 18.33/7.48 | 26.28/11.71 | 40.20/23.54 | 38.34/25.73 |
| Tan δ | 10.45/7.21 | 6.24/4.72 | 23.49/19.36 | N/A |
| TE′/°C | 41.64/43.28 | 96.12/109.07 | 235.34/238.48 | 269.92/272.39 |
| Ttanδ/°C | 39.91/42.11 | 92.72/100.55 | 214.25/218.92 | N/A |
| ΔTE′/°C | 2.18 | 12.95 | 3.14 | 2.47 |
| ΔTtanδ/°C | 2.20 | 7.83 | 4.67 | N/A |
| Peptide | Structure | Ecoh/kJ·mol−1 (without H-Bond) | Degrees of Freedom N | Molar Fraction as Counted in AA Sequence B Mori |
|---|---|---|---|---|
| Peptidebase(-R group) | -C-CO-NH- | 24.3 | 6 | 0 |
| Glycine(G) | -H | 0 | 0 | 47.5% |
| Alanine(A) | -CH3 | 4.5 | 2 | 31.7% |
| Serine(S) | -CH2-OH | 10.8 | 3 | 15.8% |
| Glutamine(Q) | -CH2-CH2-CO-NH2 | 28.8 | 5 | 0 |
| Tyrosine(Y) | -CH2-Ph-OH | 35.8 | 4 | 5% |
| Leucine(L) | -CH2-C(CH3)2 | 18 | 4 | 0 |
| Arginine(R) | -CH2-CH2-CH2-NH-C(NH2)2 | 45 | 7 | 0 |
| Average | B. Mori | 29.2 | 6 | / |
| Sample | Group | H-Bonds | Ecoh/kJ·mol−1 | N | Tgc/°C | Tg/°C | Tan δc | Tan δ | fdis |
|---|---|---|---|---|---|---|---|---|---|
| Chin | G0.475A0.317S0.158Y0.005 | 1 2 | 39.2 49.2 | 6 6 | 157.6 243.1 | 214.25 | 56 70 | 23.49 | 0.63 0.51 |
| Thai | G0.475A0.317S0.158Y0.005 | 1 2 | 39.2 49.2 | 6 6 | 157.6 243.1 | 218.92 | 56 70 | 19.36 | 0.52 0.42 |
| Sample | [CaCl2]/wt % | Tgs/°C | ΔCp/J·g−1·°C−1 | Tg-α1/°C | Content in α1 Region/% | Tan δ-α1 | fdis-α1 | Tg-α2/°C | Content in α2 Region/% | Tan δ-α2 | fdis-α2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CSF | 1.0 | 176.88 | 0.1667 | 157.53 | 32.87 | 6.65 | 0.18 | 177.11 | 67.13 | 7.52 | 0.20 |
| 1.5 | 172.65 | 0.1721 | 155.49 | 52.56 | 7.15 | 0.19 | 171.47 | 47.44 | 7.92 | 0.21 | |
| 2.0 | 169.04 | 0.1890 | 155.16 | 53.95 | 7.89 | 0.21 | 168.32 | 46.05 | 8.91 | 0.24 | |
| 3.0 | 167.42 | 0.1998 | 154.87 | 71.53 | 9.89 | 0.27 | 165.51 | 28.47 | 9.25 | 0.25 | |
| 4.0 | 163.21 | 0.2157 | 154.39 | 73.54 | 11.57 | 0.3 | 163.93 | 26.46 | 10.37 | 0.27 | |
| 6.0 | 157.30 | 0.2204 | 153.92 | 79.99 | 12.44 | 0.34 | 162.36 | 20.01 | 11.03 | 0.30 | |
| TSF | 1.0 | 181.54 | 0.1641 | 186.14 | 54.70 | 4.34 | 0.12 | 216.94 | 45.30 | 4.02 | 0.10 |
| 1.5 | 177.08 | 0.1643 | 184.54 | 65.51 | 5.73 | 0.15 | 212.01 | 34.49 | 4.97 | 0.13 | |
| 2.0 | 175.94 | 0.1644 | 184.31 | 71.14 | 6.52 | 0.18 | 209.27 | 28.86 | 5.56 | 0.14 | |
| 3.0 | 173.42 | 0.1972 | 183.69 | 75.24 | 7.22 | 0.19 | 206.45 | 24.76 | 6.25 | 0.16 | |
| 4.0 | 164.01 | 0.2136 | 183.08 | 75.72 | 8.93 | 0.23 | 204.85 | 24.28 | 7.67 | 0.20 | |
| 6.0 | 159.20 | 0.2137 | 182.47 | 76.65 | 10.17 | 0.26 | 200.82 | 23.35 | 8.93 | 0.23 |
| CSF | TSF | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [CaCl2] (wt %) | β-Sheet/% | Turns/% | Side Chains% | α-Helix/% | Random Coils/% | β-Sheet/% | Turns/% | Side Chains/% | α-Helix/% | Random Coils/% |
| 1.0 | 23.32 | 6.03 | 1.33 | 10.07 | 59.25 | 26.60 | 7.11 | 1.63 | 8.59 | 56.07 |
| 1.5 | 20.25 | 7.59 | 1.07 | 11.39 | 59.70 | 24.76 | 8.02 | 1.15 | 9.96 | 56.11 |
| 2.0 | 13.56 | 12.05 | 0.91 | 13.78 | 59.70 | 14.70 | 14.31 | 1.19 | 12.54 | 57.26 |
| 3.0 | 8.09 | 14.13 | 0.85 | 18.79 | 58.14 | 10.92 | 16.61 | 0.94 | 18.22 | 53.31 |
| 4.0 | 8.17 | 15.41 | 0.63 | 25.66 | 50.13 | 8.25 | 17.05 | 0.79 | 21.83 | 52.08 |
| 6.0 | 6.83 | 15.89 | 0.57 | 30.26 | 46.45 | 7.07 | 17.74 | 0.37 | 28.39 | 46.43 |
| CSF | TSF | |||||
|---|---|---|---|---|---|---|
| [CaCl2]/wt % | Initial Slope | Yield Stress/MPa | Strain/% | Initial Slope | Yield Stress/MPa | Strain/% |
| 1.0 | 7.86 ± 0.10 | 14.91 ± 1.57 | 1.21 ± 0.08 | 7.37 ± 0.24 | 14.28 ± 1.29 | 1.86 ± 0.07 |
| 1.5 | 7.11 ± 0.32 | 14.30 ± 1.38 | 2.15 ± 0.15 | 6.94 ± 0.19 | 13.33 ± 1.37 | 2.27 ± 0.10 |
| 2.0 | 5.48 ± 0.55 | 13.98 ± 1.55 | 2.47 ± 0.13 | 3.57 ± 0.36 | 12.45 ± 1.56 | 2.50 ± 0.05 |
| 3.0 | 2.96 ± 0.37 | 13.66 ± 1.29 | 3.39 ± 0.16 | 2.70 ± 0.27 | 11.20 ± 1.28 | 3.93 ± 0.12 |
| 4.0 | 2.16 ± 0.86 | 12.97 ± 1.37 | 4.17 ± 0.09 | 1.80 ± 0.58 | 10.17 ± 1.35 | 5.45 ± 0.27 |
| 6.0 | 1.83 ± 0.27 | 11.43 ± 0.98 | 5.88 ± 0.17 | 1.52 ± 0.49 | 8.93 ± 1.88 | 6.96 ± 0.16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Wang, F.; Gu, Z.; Ma, Q.; Hu, X. Exploring the Structural Transformation Mechanism of Chinese and Thailand Silk Fibroin Fibers and Formic-Acid Fabricated Silk Films. Int. J. Mol. Sci. 2018, 19, 3309. https://doi.org/10.3390/ijms19113309
Liu Q, Wang F, Gu Z, Ma Q, Hu X. Exploring the Structural Transformation Mechanism of Chinese and Thailand Silk Fibroin Fibers and Formic-Acid Fabricated Silk Films. International Journal of Molecular Sciences. 2018; 19(11):3309. https://doi.org/10.3390/ijms19113309
Chicago/Turabian StyleLiu, Qichun, Fang Wang, Zhenggui Gu, Qingyu Ma, and Xiao Hu. 2018. "Exploring the Structural Transformation Mechanism of Chinese and Thailand Silk Fibroin Fibers and Formic-Acid Fabricated Silk Films" International Journal of Molecular Sciences 19, no. 11: 3309. https://doi.org/10.3390/ijms19113309
APA StyleLiu, Q., Wang, F., Gu, Z., Ma, Q., & Hu, X. (2018). Exploring the Structural Transformation Mechanism of Chinese and Thailand Silk Fibroin Fibers and Formic-Acid Fabricated Silk Films. International Journal of Molecular Sciences, 19(11), 3309. https://doi.org/10.3390/ijms19113309