Using Spectral Representation to Classify Proteins’ Conformational States
Abstract
:1. Introduction
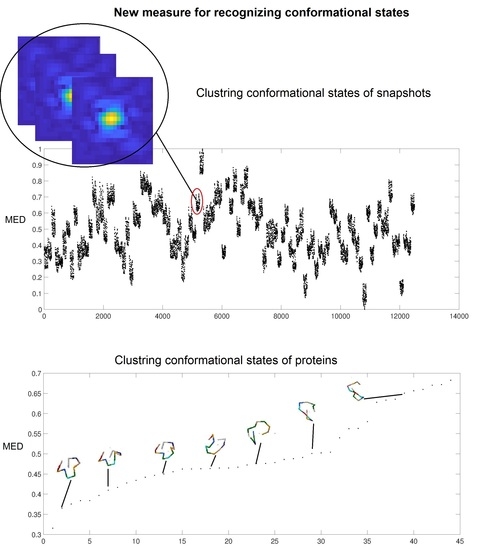
2. Results and Discussion
3. Method
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MED | Maximum Eigenvalue Of Distance Matrix |
References
- Raveh, B.; Enosh, A.; Schueler-Furman, O.; Halperin, D. Rapid Sampling of Molecular Motions with Prior Information Constraints. PLoS Comput. Biol. 2009, 5, e1000295. [Google Scholar] [CrossRef] [PubMed]
- Head-Gordon, T.; Brown, S. Minimalist models for protein folding and design. Curr. Opin. Struct. Biol. 2003, 13, 160–167. [Google Scholar] [CrossRef]
- Whitford, P.C.; Miyashita, O.; Levy, Y.; Onucic, J.N. Conformational Transitions of Adenylate Kinase: Switching by Cracking. J. Mol. Biol. 2007, 366, 1661–1671. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyashita, O.; Wolynes, P.G.; Onucic, J.N. Simple Energy Landscape Model for the Kinetics of Functional Transitions in Proteins. J. Phys. Chem. B 2005, 109, 1959–1969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keskin, O.; Bahar, I.; Flatow, D.; Covell, D.; Jernigan, R. Molecular mechanisms of chaperonin GroEL-GroES function. Biochemistry 2002, 41, 491–501. [Google Scholar] [CrossRef] [PubMed]
- Temiz, N.; Meirovitch, E.; Bahar, I. Escherichia coli adenylate kinase dynamics: Comparison of elastic network model modes with mode-coupling 15NNMR relaxation data. Proteins 2004, 57, 468–480. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Rader, A.; Bahar, I.; Jernigan, R. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 2004, 147, 302–314. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, M. Comment on Elastic Network Models and Proteins. Phys. Biol. 2007, 4, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Brooks, B. Identification of dynamical correlations within the myosin motor domain by the normal mode analysis of an elastic network model. J. Mol. Biol. 2005, 346, 745–759. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Thorpe, M. A Natural Coarse Graining for Simulating Large Biomolecular Motion. Biophys. J. 2006, 91, 2115–2120. [Google Scholar] [CrossRef] [PubMed]
- Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, B.J., Ciccoti, G., Coker, D.F., Eds.; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
- Weiss, D.; Levitt, M. Can morphing methods predict intermediate structures? J. Mol. Biol. 2009, 385, 665–674. [Google Scholar] [CrossRef] [PubMed]
- Schuyler, A.; Jernigan, R.; Qasba, P.; Ramakrishnan, B.; Chirikjian, G. Iterative cluster-NMA: A tool for generating conformational transitions in proteins. Proteins 2009, 74, 760–776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schroeder, G.; Brunger, A.T.; Levitt, M. Combining Efficient Conformational Sampling with a Deformable Elastic Network Model Facilitates Structure Refinement at Low Resolution. Structure 2007, 15, 1630–1641. [Google Scholar] [CrossRef] [PubMed]
- Choset, H.; Lynch, K.M.; Hutchinson, S.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Kavraki, L.E.; Švestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Haspel, N.; Moll, M.; Baker, M.L.; Chiu, W.; Kavraki, L.E. Tracing conformational changes in proteins. BMC Struct. Biol. 2010, 10 (Suppl. 1), S1. [Google Scholar] [CrossRef] [PubMed]
- Siegfried, H.; Reich, S.E.W. Structure-based drug design (SBDD): Every structure tells a story…. Perspect. Drug Discov. Design 1993, 1, 371–390. [Google Scholar]
- Cammarata, M.; Levantino, M.; Schotte, F.; Anfinrud, P.A.; Ewald, F.; Choi, J.; Cupane, A.; Wulff, M.; Ihee, H. Tracking the structural dynamics of proteins in solution using time-resolved wide-angle X-ray scattering. Nat. Methods 2008, 5, 881–886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saberi Fathi, S.M.; White, D.T.; Tuszynski, J.A. Geometrical comparison of two protein structures using Wigner-D functions. Proteins 2014, 82, 2756–2769. [Google Scholar] [CrossRef] [PubMed]
- Howells, M.R.; Beetz, T.; Chapman, C.; Cui, C.; Holton, J.M.; Jacobsen, C.J.; Kirz, J.; Lima, E.; Marchesini, S.; Miao, H.; et al. An assessment of the resolution limitation due to radiation-damage in X-ray diffraction microscopy. J. Electron Spectrosc. Relat. Phenom. 2009, 170, 4–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravelli, R.B.G.; Garman, E.F. Radiation damage in macromolecular cryocrystallography. Curr. Opin. Struct. Biol. 2006, 16, 624–629. [Google Scholar] [CrossRef] [PubMed]
- Frank, J. Single-particle reconstruction of biological macromolecules in electron microscopy—30 Years. Q. Rev. Biophys. 2009, 42, 139–158. [Google Scholar] [CrossRef] [PubMed]
- Fung, R.; Shneerson, V.; Saldin, D.K.; Ourmazd, A. Structure from Fleeting Illumination of Faint Spinning Objects in Flight? Nat. Phys. 2009, 5, 64–67. [Google Scholar] [CrossRef]
- Schwander, P.; Fung, R.; Phillips, G.N., Jr.; Ourmazd, A. Mapping the conformations of biological assemblies. New J. Phys. 2010, 12, 035007. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levantino, M.; Yorke, B.A.; Monteiro, D.C.F.; Cammarata, M.; Pearson, A.R. Time-resolved experiments at XFELs and synchrotrons. Curr. Opin. Struct. Biol. 2015, 35, 41–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coppens, P.; Pitak, M.; Gembicky, M.; Messerschmidt, M.; Scheins, S.; Benedict, J.; Adachi, S.I.; Sato, T.; Nozawa, S.; Ichiyanagi, K.; et al. The RATIO method for time-resolved Laue crystallography. J. Synchrotron. Radiat. 2009, 16, 226–230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coppens, P.; Fournier, B. New methods in time-resolved Laue pump-probe crystallography at synchrotron sources. J. Synchrotron Radiat. 2015, 22, 280–287. [Google Scholar] [CrossRef] [PubMed]
- Schotte, F.; Cho, H.S.; Kaila, V.R.; Kamikubo, H.; Dashdorj, N.; Henry, E.R.; Graber, T.J.; Henning, R.; Wulff, M.; Hummer, G.; et al. Watching a signaling protein function in real time via 100-ps time-resolved Laue crystallography. Proc. Natl. Acad. Sci. USA 2012, 109, 19256–19261. [Google Scholar] [CrossRef] [PubMed]
- Yorke, B.A.; Beddard, G.S.; Owen, R.L.; Pearson, A.R. Time-resolved crystallography using the Hadamard transform. Nat. Methods 2014, 11, 1131–1134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saberi Fathi, S.M. A new definition and properties of the similarity value between two protein structures. J. Biol. Phys. 2016, 42, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Wigner, E.P. Gruppentheorie und Ihre Anwendungen auf die Quantenmechanik der Atomspektren; Vieweg Verlag: Braunschweig, Germany, 1931. [Google Scholar]
- Potts, D.; Prestin, J.; Vollrath, A. A fast algorithm for nonequispaced Fourier transforms on the rotation group. Number. Algorithms 2009, 52, 355–384. [Google Scholar] [CrossRef] [Green Version]
- Hielscher, R.; Potts, D.; Prestin, J.; Schaeben, H.; Schmalz, M. The Radon transform on SO3: A Fourier slice theorem and numerical inversion. Inverse Probl. 2008, 24, 025011. [Google Scholar] [CrossRef]
- Lipson, H.; Taylor, C.A. Fourier Transforms and X-ray Diffraction; Bell: London, UK, 1958. [Google Scholar]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M.; Svensén, M.; Williams, C.K.I. GTM: The Generative Topographic Mapping. Neural Comput. 1998, 10, 215–234. [Google Scholar] [CrossRef] [Green Version]
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S.W. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proc. Nat. Acad. Sci. USA 2005, 102, 7426–7431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coifman, R.R.; Kevrekidis, I.G.; Lafon, S.; Maggioni, M.; Nadler, B. Diffusion maps, reduction coordinates, and low dimensional representation of stochastic systems. Multiscale Model. Simul. 2008, 7, 842–864. [Google Scholar] [CrossRef]
- Jones, P.W.; Maggioni, M.; Schul, R. Manifold parametrizations by eigenfunctions of the Laplacian and heat kernels. Proc. Nat. Acad. Sci. USA 2008, 105, 1803–1808. [Google Scholar] [CrossRef] [PubMed]
- Lerman, G.; Shakhnovich, B.E. Defining functional distance using manifold embeddings of gene ontology annotations. Proc. Nat. Acad. Sci. USA 2007, 104, 11334–11339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rajan, A.; Freddolino, P.L.; Schulten, K. Going beyond Clustering in MD Trajectory Analysis: An Application to Villin Headpiece Folding. PLoS ONE 2010, 5, e9890. [Google Scholar] [CrossRef] [PubMed]
- Putnam, D.K.; Lowe, E.W., Jr.; Meiler, J. Reconstruction of SAXS Profiles from Protein Structures. Comput. Struct. Biotechnol. J. 2013, 8, e201308006. [Google Scholar] [CrossRef] [PubMed]





| Peptide Name | MED |
|---|---|
| s1-17 | 0.41669 |
| s1-18 | 0.44192 |
| s1-21 | 0.3754 |
| s1-1 | 0.46476 |
| s1-10 | 0.46306 |
| s1-11 | 0.46238 |
| s1-12 | 0.5023 |
| s1-13 | 0.39675 |
| s1-14 | 0.47616 |
| s1-15 | 0.48602 |
| s1-16 | 0.43416 |
| s1-19 | 0.45545 |
| s1-2 | 0.40972 |
| s1-20 | 0.48793 |
| s1-3 | 0.50093 |
| s1-4 | 0.31545 |
| s1-5 | 0.47582 |
| s1-6 | 0.46336 |
| s1-7 | 0.38409 |
| s1-8 | 0.36499 |
| s1-9 | 0.47234 |
| s14-1 | 0.65987 |
| s14-10 | 0.63324 |
| s14-11 | 0.62796 |
| s14-2 | 0.49089 |
| s14-3 | 0.68266 |
| s14-4 | 0.67186 |
| s14-5 | 0.63556 |
| s14-6 | 0.67026 |
| s14-7 | 0.5799 |
| s14-8 | 0.65054 |
| s14-9 | 0.65645 |
| s16-1 | 0.46471 |
| s16-2 | 0.56308 |
| s16-3 | 0.46227 |
| s16-4 | 0.53976 |
| s16-5 | 0.44666 |
| s16-6 | 0.38378 |
| s16-7 | 0.56239 |
| s31-1 | 0.47829 |
| s31-2 | 0.50418 |
| s31-3 | 0.4668 |
| s31-4 | 0.44994 |
| s31-5 | 0.42765 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saberi Fathi, S.M.; Tuszynski, J.A. Using Spectral Representation to Classify Proteins’ Conformational States. Int. J. Mol. Sci. 2018, 19, 2089. https://doi.org/10.3390/ijms19072089
Saberi Fathi SM, Tuszynski JA. Using Spectral Representation to Classify Proteins’ Conformational States. International Journal of Molecular Sciences. 2018; 19(7):2089. https://doi.org/10.3390/ijms19072089
Chicago/Turabian StyleSaberi Fathi, Seyed Majid, and Jack A. Tuszynski. 2018. "Using Spectral Representation to Classify Proteins’ Conformational States" International Journal of Molecular Sciences 19, no. 7: 2089. https://doi.org/10.3390/ijms19072089
APA StyleSaberi Fathi, S. M., & Tuszynski, J. A. (2018). Using Spectral Representation to Classify Proteins’ Conformational States. International Journal of Molecular Sciences, 19(7), 2089. https://doi.org/10.3390/ijms19072089