Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5
Abstract
:1. Introduction
2. Results and Discussion
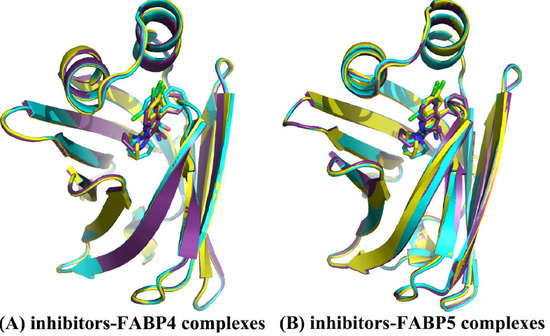
2.1. Equilibrium and Flexibilities of Systems during Molecular Dynamics Simulations
2.2. Differences in Internal Dynamics of FABP4 and FABP5
2.3. Principal Component Analyses
2.4. Binding Free Energy Analysis
2.5. Contributions of Separated Residues to Inhibitor Bindings
3. Materials and Methods
3.1. Molecular Docking
3.2. Molecular Dynamics Simulations
3.3. Principal Component Analysis
3.4. MM-GBSA Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| FABP4 and FABP5 | Fatty acid binding proteins 4 and 5 |
| MD | Molecular dynamics |
| MM-GBSA | Molecular mechanics generalized Born surface area |
| MM-PBSA | Molecular mechanics Poisson Boltzmann surface area |
| FABPs | Fatty acid binding proteins |
| L-FABP/FABP1 | Liver FABP |
| I-FABP/FABP2 | Intestinal FABP |
| H-FABP/FABP3 | Heart FABP |
| A-FABP/FABP4/aP2 | Adipocyte FABP |
| E-FABP/FABP5/mal1 | Epidermal FABP |
| Il-FABP/FABP6 | Ileal FABP |
| B-FABP/FABP7 | Brain FABP |
| M-FABP/FABP8 | Myelin FABP |
| T-FABP/FABP9 | Testis FABP |
| LGA | Lamarckian genetic algorithm |
| GAFF | General Amber force field |
| PME | Particle mesh Ewald |
| RMSDs | Root mean square deviations |
| RMSFs | Root mean square fluctuations |
References
- Haunerland, N.H.; Spener, F. Fatty acid-binding proteins—Insights from genetic manipulations. Prog. Lipid Res. 2004, 43, 328–349. [Google Scholar] [CrossRef] [PubMed]
- Chmurzyńska, A. The multigene family of fatty acid-binding proteins (FABPs): Function, structure and polymorphism. J. Appl. Genet. 2006, 47, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Makowski, L.; Hotamisligil, G.S. The role of fatty acid binding proteins in metabolic syndrome and atherosclerosis. Curr. Opin. Lipidol. 2005, 16, 543–548. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coe, N.R.; Bernlohr, D.A. Physiological properties and functions of intracellular fatty acid-binding proteins. Biochim. Biophys. Acta 1998, 1391, 287–306. [Google Scholar] [CrossRef]
- Ockner, R.K.; Manning, J.A.; Poppenhausen, R.B.; Ho, W.K.L. A Binding Protein for Fatty Acids in Cytosol of Intestinal Mucosa, Liver, Myocardium, and Other Tissues. Science 1972, 177, 56–58. [Google Scholar] [CrossRef] [PubMed]
- Veerkamp, J.H.; van Moerkerk, H.T.B. Fatty acid-binding protein and its relation to fatty acid oxidation. Mol. Cell. Biochem. 1993, 123, 101–106. [Google Scholar] [CrossRef] [PubMed]
- Hotamisligil, G.S. Inflammation and metabolic disorders. Nature 2006, 444, 860–867. [Google Scholar] [CrossRef] [PubMed]
- Furuhashi, M.; Hotamisligil, G.S. Fatty acid-binding proteins: Role in metabolic diseases and potential as drug targets. Nat. Rev. Drug Discov. 2008, 7, 489–503. [Google Scholar] [CrossRef] [PubMed]
- Hunt, C.R.; Ro, J.H.; Dobson, D.E.; Min, H.Y.; Spiegelman, B.M. Adipocyte P2 gene: Developmental expression and homology of 5′-flanking sequences among fat cell-specific genes. Proc. Natl. Acad. Sci. USA 1986, 83, 3786–3790. [Google Scholar] [CrossRef] [PubMed]
- Pelton, P.D.; Zhou, L.; Demarest, K.T.; Burris, T.P. PPARγ Activation Induces the Expression of the Adipocyte Fatty Acid Binding Protein Gene in Human Monocytes. Biochem. Biophys. Res. Commun. 1999, 261, 456–458. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Luo, N.; Lopes-Virella, M.F.; Garvey, W.T. The adipocyte lipid binding protein (ALBP/aP2) gene facilitates foam cell formation in human THP-1 macrophages. Atherosclerosis 2002, 165, 259–269. [Google Scholar] [CrossRef]
- Kazemi, M.R.; McDonald, C.M.; Shigenaga, J.K.; Grunfeld, C.; Feingold, K.R. Adipocyte fatty acid-binding protein expression and lipid accumulation are increased during activation of murine macrophages by toll-like receptor agonists. Arterioscler. Thromb. Vasc. Biol. 2005, 25, 1220–1224. [Google Scholar] [CrossRef] [PubMed]
- Rolph, M.S.; Young, T.R.; Shum, B.O.V.; Gorgun, C.Z.; Schmitz-Peiffer, C.; Ramshaw, I.A.; Hotamisligil, G.S.; Mackay, C.R. Regulation of Dendritic Cell Function and T Cell Priming by the Fatty Acid-Binding Protein aP2. J. Immunol. 2006, 177, 7794–7801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uysal, K.T.; Scheja, L.; Wiesbrock, S.M.; Bonner-Weir, S.; Hotamisligil, G.K.S. Improved Glucose and Lipid Metabolism in Genetically Obese Mice Lacking aP2. Endocrinology 2000, 141, 3388–3396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sulsky, R.; Magnin, D.R.; Huang, Y.; Simpkins, L.; Taunk, P.; Patel, M.; Zhu, Y.; Stouch, T.R.; Bassolino-Klimas, D.; Parker, R.; et al. Potent and selective biphenyl azole inhibitors of adipocyte fatty acid binding protein (aFABP). Bioorg. Med. Chem. Lett. 2007, 17, 3511–3515. [Google Scholar] [CrossRef] [PubMed]
- Hirosumi, J.; Tuncman, G.; Chang, L.; Gorgun, C.Z.; Uysal, K.T.; Maeda, K.; Karin, M.; Hotamisligil, G.S. A central role for JNK in obesity and insulin resistance. Nature 2002, 420, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Hotamisligil, G.S.; Johnson, R.S.; Distel, R.J.; Ellis, R.; Papaioannou, V.E.; Spiegelman, B.M. Uncoupling of obesity from insulin resistance through a targeted mutation in aP2, the adipocyte fatty acid binding protein. Science 1996, 274, 1377–1379. [Google Scholar] [CrossRef] [PubMed]
- Boord, J.B.; Maeda, K.; Makowski, L.; Babaev, V.R.; Fazio, S.; Linton, M.F.; Hotamisligil, G.S. Adipocyte Fatty Acid–Binding Protein, aP2, Alters Late Atherosclerotic Lesion Formation in Severe Hypercholesterolemia. Arterioscler. Thromb. Vasc. Biol. 2002, 22, 1686–1691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boord, J.B.; Maeda, K.; Makowski, L.; Babaev, V.R.; Fazio, S.; Linton, M.F.; Hotamisligil, G.S. Combined adipocyte-macrophage fatty acid-binding protein deficiency improves metabolism, atherosclerosis, and survival in apolipoprotein E-deficient mice. Circulation 2004, 110, 1492–1498. [Google Scholar] [CrossRef] [PubMed]
- Maeda, K.; Uysal, K.T.; Makowski, L.; Görgün, C.Z.; Atsumi, G.; Parker, R.A.; Brüning, J.; Hertzel, A.V.; Bernlohr, D.A.; Hotamisligil, G.S. Role of the Fatty Acid Binding Protein mal1 in Obesity and Insulin Resistance. Diabetes 2003, 52, 300–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Furuhashi, M.; Fucho, R.; Görgün, C.Z.; Tuncman, G.; Cao, H.; Hotamisligil, G.S. Adipocyte/macrophage fatty acid–binding proteins contribute to metabolic deterioration through actions in both macrophages and adipocytes in mice. J. Clin. Investig. 2008, 118, 2640–2650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erbay, E.; Babaev, V.R.; Mayers, J.R.; Makowski, L.; Charles, K.N.; Snitow, M.E.; Fazio, S.; Wiest, M.M.; Watkins, S.M.; Linton, M.F.; et al. Reducing endoplasmic reticulum stress through a macrophage lipid chaperone alleviates atherosclerosis. Nat. Med. 2009, 15, 1383–1391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, A.; Wang, Y.; Xu, J.Y.; Stejskal, D.; Tam, S.; Zhang, J.; Wat, N.M.S.; Wong, W.K.; Lam, K.S.L. Adipocyte Fatty Acid–Binding Protein Is a Plasma Biomarker Closely Associated with Obesity and Metabolic Syndrome. Clin. Chem. 2006, 52, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Yeung, D.C.Y.; Xu, A.; Cheung, C.W.S.; Wat, N.M.S.; Yau, M.H.; Fong, C.H.Y.; Chau, M.T.; Lam, K.S.L. Serum adipocyte fatty acid-binding protein levels were independently associated with carotid atherosclerosis. Arterioscler. Thromb. Vasc. Biol. 2007, 27, 1796–1802. [Google Scholar] [CrossRef] [PubMed]
- Makowski, L.; Boord, J.B.; Maeda, K.; Babaev, V.R.; Uysal, K.T.; Morgan, M.A.; Parker, R.A.; Suttles, J.; Fazio, S.; Hotamisligil, G.S.; et al. Lack of macrophage fatty-acid-binding protein aP2 protects mice deficient in apolipoprotein E against atherosclerosis. Nat. Med. 2001, 7, 699–705. [Google Scholar] [CrossRef] [PubMed]
- Agardh, H.E.; Folkersen, L.; Ekstrand, J.; Marcus, D.; Swedenborg, J.; Hedin, U.; Gabrielsen, A.; Paulsson-Berne, G. Expression of fatty acid-binding protein 4/aP2 is correlated with plaque instability in carotid atherosclerosis. J. Intern. Med. 2011, 269, 200–210. [Google Scholar] [CrossRef] [PubMed]
- Hertzel, A.V.; Bennaars-Eiden, A.; Bernlohr, D.A. Increased lipolysis in transgenic animals overexpressing the epithelial fatty acid binding protein in adipose cells. J. Lipid Res. 2002, 43, 2105–2111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maeda, K.; Cao, H.; Kono, K.; Gorgun, C.Z.; Furuhashi, M.; Uysal, K.T.; Cao, Q.; Atsumi, G.; Malone, H.; Krishnan, B.; et al. Adipocyte/macrophage fatty acid binding proteins control integrated metabolic responses in obesity and diabetes. Cell Metab. 2005, 1, 107–119. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Maeda, K.; Gorgun, C.Z.; Kim, H.-J.; Park, S.-Y.; Shulman, G.I.; Kim, J.K.; Hotamisligil, G.S. Regulation of Metabolic Responses by Adipocyte/ Macrophage Fatty Acid–Binding Proteins in Leptin-Deficient Mice. Diabetes 2006, 55, 1915–1922. [Google Scholar] [CrossRef] [PubMed]
- Llaverias, G.; Noé, V.; Peñuelas, S.; Vázquez-Carrera, M.; Sánchez, R.M.; Laguna, J.C.; Ciudad, C.J.; Alegret, M. Atorvastatin reduces CD68, FABP4, and HBP expression in oxLDL-treated human macrophages. Biochem. Biophys. Res. Commun. 2004, 318, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Ren, P.; Zhang, L.; Wang, X.L.; Chen, L.; Shen, Y.H. Metformin reduces lipid accumulation in macrophages by inhibiting FOXO1-mediated transcription of fatty acid-binding protein 4. Biochem. Biophys. Res. Commun. 2010, 393, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Furuhashi, M.; Tuncman, G.; Gorgun, C.Z.; Makowski, L.; Atsumi, G.; Vaillancourt, E.; Kono, K.; Babaev, V.R.; Fazio, S.; Linton, M.F.; et al. Treatment of diabetes and atherosclerosis by inhibiting fatty-acid-binding protein aP2. Nature 2007, 447, 959–965. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zimmerman, A.W.; Veerkamp, J.H. New insights into the structure and function of fatty acid-binding proteins. Cell. Mol. Life Sci. 2002, 59, 1096–1116. [Google Scholar] [CrossRef] [PubMed]
- Floresta, G.; Pistarà, V.; Amata, E.; Dichiara, M.; Marrazzo, A.; Prezzavento, O.; Rescifina, A. Adipocyte fatty acid binding protein 4 (FABP4) inhibitors. A comprehensive systematic review. Eur. J. Med. Chem. 2017, 138, 854–873. [Google Scholar] [CrossRef] [PubMed]
- Kühne, H.; Obst-Sander, U.; Kuhn, B.; Conte, A.; Ceccarelli, S.M.; Neidhart, W.; Rudolph, M.G.; Ottaviani, G.; Gasser, R.; So, S.-S.; et al. Design and synthesis of selective, dual fatty acid binding protein 4 and 5 inhibitors. Bioorg. Med. Chem. Lett. 2016, 26, 5092–5097. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, B.; Guba, W.; Hert, J.; Banner, D.; Bissantz, C.; Ceccarelli, S.; Haap, W.; Körner, M.; Kuglstatter, A.; Lerner, C.; et al. A Real-World Perspective on Molecular Design. J. Med. Chem. 2016, 59, 4087–4102. [Google Scholar] [CrossRef] [PubMed]
- Brameld, K.A.; Kuhn, B.; Reuter, D.C.; Stahl, M. Small Molecule Conformational Preferences Derived from Crystal Structure Data. A Medicinal Chemistry Focused Analysis. J. Chem. Inf. Model. 2008, 48, 1–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, T.; Zhang, W.; Case, D.A.; Wang, W. Characterization of Domain–Peptide Interaction Interface: A Case Study on the Amphiphysin-1 SH3 Domain. J. Mol. Biol. 2008, 376, 1201–1214. [Google Scholar] [CrossRef] [PubMed]
- Cheatham, T.E.; Srinivasan, J.; Case, D.A.; Kollman, P.A. Molecular Dynamics and Continuum Solvent Studies of the Stability of PolyG-PolyC and PolyA-PolyT DNA Duplexes in Solution. J. Biomol. Struct. Dyn. 1998, 16, 265–280. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.-J.; Pang, X.-Q.; Zhang, X.; Han, K.-L. Molecular dynamics simulation reveals preorganization of the chloroplast FtsY towards complex formation induced by GTP binding. J. Struct. Biol. 2011, 173, 57–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, D.; Bai, Q.; Zhou, S.; Liu, X.; Liu, H.; Yao, X. Molecular dynamics simulation, binding free energy calculation and unbinding pathway analysis on selectivity difference between FKBP51 and FKBP52: Insight into the molecular mechanism of isoform selectivity. Proteins Struct. Funct. Genet. 2018, 86, 43–56. [Google Scholar] [CrossRef] [PubMed]
- De Vivo, M.; Masetti, M.; Bottegoni, G.; Cavalli, A. Role of Molecular Dynamics and Related Methods in Drug Discovery. J. Med. Chem. 2016, 59, 4035–4061. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Z.; Wang, J.N.; Zhu, W.L. Mutation L1196M-induced conformational changes and the drug resistant mechanism of anaplastic lymphoma kinase studied by free energy perturbation and umbrella sampling. Phys. Chem. Chem. Phys. 2017, 19, 30239–30248. [Google Scholar] [CrossRef] [PubMed]
- Wu, E.L.; Mei, Y.; Han, K.; Zhang, J.Z.H. Quantum and Molecular Dynamics Study for Binding of Macrocyclic Inhibitors to Human α-Thrombin. Biophys. J. 2007, 92, 4244–4253. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Ma, A.; Wang, J. Ligand Selectivity Mechanism and Conformational Changes in Guanine Riboswitch by Molecular Dynamics Simulations and Free Energy Calculations. J. Chem. Inf. Model. 2017, 57, 918–928. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Zhu, T.; Ji, C.; Zhang, Q.; Zhang, J.Z. Direct folding simulation of helical proteins using an effective polarizable bond force field. Phys. Chem. Chem. Phys. 2017, 19, 15273–15284. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Morin, P.; Wang, W.; Kollman, P.A. Use of MM-PBSA in Reproducing the Binding Free Energies to HIV-1 RT of TIBO Derivatives and Predicting the Binding Mode to HIV-1 RT of Efavirenz by Docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. [Google Scholar] [CrossRef] [PubMed]
- Massova, I.; Kollman, P.A. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discov. Des. 2000, 18, 113–135. [Google Scholar] [CrossRef]
- Gohlke, H.; Case, D.A. Converging free energy estimates: MM-PB(GB)SA studies on the protein–protein complex Ras–Raf. J. Comput. Chem. 2004, 25, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemometr. Intell. Lab. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Chen, J. Functional roles of magnesium binding to extracellular signal-regulated kinase 2 explored by molecular dynamics simulations and principal component analysis. J. Biomol. Struct. Dyn. 2018, 36, 351–361. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into Protein–Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras–Raf and Ras–RalGDS Complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Hunter, N.H.; Bakula, B.C.; Bruce, C.D. Molecular dynamics simulations of apo and holo forms of fatty acid binding protein 5 and cellular retinoic acid binding protein II reveal highly mobile protein, retinoic acid ligand, and water molecules. J. Biomol. Struct. Dyn. 2018, 36, 1893–1907. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, X.; Dong, Z. Concerted Dynamic Motions of an FABP4 Model and Its Ligands Revealed by Microsecond Molecular Dynamics Simulations. Biochemistry 2014, 53, 6409–6417. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Zhu, L.; Yu, D.; Cao, Z.; Kang, T.; Zhu, R. The Stereoselectivity of CYP2C19 on R- and S-isomers of Proton Pump Inhibitors. Chem. Biol. Drug Des. 2014, 83, 610–621. [Google Scholar] [CrossRef] [PubMed]
- Goodsell, D.S.; Morris, G.M.; Olson, A.J. Automated docking of flexible ligands: Applications of AutoDock. J. Mol. Recognit. 1996, 9, 1–5. [Google Scholar] [CrossRef]
- Cai, H.; Yan, G.; Zhang, X.; Gorbenko, O.; Wang, H.; Zhu, W. Discovery of highly selective inhibitors of human fatty acid binding protein 4 (FABP4) by virtual screening. Bioorg. Med. Chem. Lett. 2010, 20, 3675–3679. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Betz, R.M.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; Homeyer, N.; et al. AMBER 16; University of California: San Francisco, CA, USA, 2016. [Google Scholar]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef] [PubMed]
- Jakalian, A.; Bush, B.L.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic Charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Genet. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Chen, J. Drug resistance mechanisms of three mutations V32I, I47V and V82I in HIV-1 protease toward inhibitors probed by molecular dynamics simulations and binding free energy predictions. RSC Adv. 2016, 6, 58573–58585. [Google Scholar] [CrossRef]
- Coleman, T.G.; Mesick, H.C.; Darby, R.L. Numerical integration. Ann. Biomed. Eng. 1977, 5, 322–328. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins Struct. Funct. Genet. 1991, 11, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Laberge, M.; Yonetani, T. Molecular Dynamics Simulations of Hemoglobin A in Different States and Bound to DPG: Effector-Linked Perturbation of Tertiary Conformations and HbA Concerted Dynamics. Biophys. J. 2008, 94, 2737–2751. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, A.D. Gene duplications in the structural evolution of chymotrypsin. J. Mol. Biol. 1979, 128, 49–79. [Google Scholar] [CrossRef]
- Wu, E.L.; Han, K.; Zhang, J.Z.H. Selectivity of Neutral/Weakly Basic P1 Group Inhibitors of Thrombin and Trypsin by a Molecular Dynamics Study. Chem. Eur. J. 2008, 14, 8704–8714. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.L.; Feng, G.Q.; Wang, X.W.; Wang, L.Z.; Zhang, Q.G. Effect of electrostatic polarization and bridging water on CDK2-ligand binding affinities calculated using a highly efficient interaction entropy method. Phys. Chem. Chem. Phys. 2017, 19, 10140–10152. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.D.; Ma, A.J.; Dou, X.H.; Zhao, L.L.; Wang, J.H. Computational Studies of a Mechanism for Binding and Drug Resistance in the Wild Type and Four Mutations of HIV-1 Protease with a GRL-0519 Inhibitor. Int. J. Mol. Sci. 2016, 17, 15. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, J.; Zhu, W. Zinc ion-induced conformational changes in new Delphi metallo-β-lactamase 1 probed by molecular dynamics simulations and umbrella sampling. Phys. Chem. Chem. Phys. 2017, 19, 3067–3075. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.; Liu, X.; Zhang, J.Z.H. Interaction Entropy: A New Paradigm for Highly Efficient and Reliable Computation of Protein–Ligand Binding Free Energy. J. Am. Chem. Soc. 2016, 138, 5722–5728. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Liu, X.; Zhang, S.; Su, J.; Zhang, Q.; Chen, J. Computational revelation of binding mechanisms of inhibitors to endocellular protein tyrosine phosphatase 1B using molecular dynamics simulations. J. Biomol. Struct. Dyn. 2017. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Liu, X.; Zhang, S.; Yan, F.; Zhang, Q.; Chen, J. A theoretical insight into selectivity of inhibitors toward two domains of bromodomain-containing protein 4 using molecular dynamics simulations. Chem. Biol. Drug Des. 2018, 91, 828–840. [Google Scholar] [CrossRef] [PubMed]
- Bai, Q.F.; Perez-Sanchez, H.; Shi, Z.Y.; Li, L.L.; Shi, D.F.; Liu, H.X.; Yao, X.J. Computational studies on horseshoe shape pocket of human orexin receptor type 2 and boat conformation of suvorexant by molecular dynamics simulations. Chem. Biol. Drug Des. 2018, 92, 1221–1231. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Liu, H.; Sun, H.Y.; Pan, P.C.; Li, Y.Y.; Li, D.; Hou, T.J. Assessing the performance of the MM/PBSA and MM/GBSA methods. 6. Capability to predict protein-protein binding free energies and re-rank binding poses generated by protein-protein docking. Phys. Chem. Chem. Phys. 2016, 18, 22129–22139. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.Y.; Li, Y.Y.; Shen, M.Y.; Tian, S.; Xu, L.; Pan, P.C.; Guan, Y.; Hou, T.J. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.Y.; Li, Y.Y.; Tian, S.; Xu, L.; Hou, T.J. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Sun, H.Y.; Li, Y.Y.; Wang, J.M.; Hou, T.J. Assessing the Performance of MM/PBSA and MM/GBSA Methods. 3. The Impact of Force Fields and Ligand Charge Models. J. Phys. Chem. B 2013, 117, 8408–8421. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Wang, J.; Li, Y.; Wang, W. Assessing the Performance of the MM/PBSA and MM/GBSA Methods. 1. The Accuracy of Binding Free Energy Calculations Based on Molecular Dynamics Simulations. J. Chem. Inf. Model. 2011, 51, 69–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sitkoff, D.; Sharp, K.A.; Honig, B. Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 1994, 98, 1978–1988. [Google Scholar] [CrossRef]
- Tavanti, F.; Pedone, A.; Menziani, M.C. Computational Insight into the Effect of Natural Compounds on the Destabilization of Preformed Amyloid-β (1-40) Fibrils. Molecules 2018, 23, 1320. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Shen, H.; Zhu, X.; Li, G. Fast and accurate computation schemes for evaluating vibrational entropy of proteins. J. Comput. Chem. 2011, 32, 3188–3193. [Google Scholar] [CrossRef] [PubMed]







| Energy | 5M7-FABP4 | 5M7-FABP5 | 65X-FABP4 | 65X-FABP5 | 65Z-FABP4 | 65Z-FABP5 |
|---|---|---|---|---|---|---|
| −104.54 ± 7.18 | −96.97 ± 6.79 | −114.18 ± 4.99 | −100.35 ± 8.13 | −112.32 ± 4.96 | −98.56 ± 7.75 | |
| −42.24 ± 2.35 | −44.69 ± 2.36 | −44.33 ± 2.52 | −45.59 ± 3.17 | −42.67 ± 2.45 | −44.31 ± 2.56 | |
| 115.18 ± 3.84 | 113.10 ± 6.26 | 124.30 ± 4.31 | 116.24 ± 5.79 | 122.76 ± 3.77 | 113.31 ± 4.71 | |
| −6.07 ± 0.16 | −6.11 ± 0.13 | −6.36 ± 0.12 | −6.41 ± 0.13 | −6.02 ± 0.14 | −6.33 ± 0.13 | |
| b | 10.64 ± 2.96 | 16.13 ± 2.35 | 10.12 ± 2.10 | 15.98 ± 2.11 | 10.44 ± 2.72 | 14.74 ± 2.14 |
| 23.75 ± 4.68 | 25.21 ± 5.96 | 24.96 ± 6.95 | 23.15 ± 5.33 | 23.91 ± 5.23 | 23.74 ± 6.13 | |
| c | −13.92 | −9.46 | −15.61 | −12.96 | −14.35 | −12.16 |
| d | −10.52 | −8.66 | −10.94 | −9.71 | −10.71 | −9.50 |
| Compound | a Hydrogen Bonds | Distance (Å) | Angle (°) | b Occupancy (%) |
|---|---|---|---|---|
| FABP4-5M7 | Arg126-NH2-HH21···5M7-O18 | 2.8 | 157.6 | 99.8 |
| Arg126-NE-HE···5M7-O18 | 3.1 | 137.8 | 79.4 | |
| Tyr128-OH-HH···5M7-O18 | 3.2 | 128.1 | 4.5 | |
| FABP5-5M7 | Arg129-NH2-HH21···5M7-O18 | 2.8 | 154.4 | 95.9 |
| Arg129-NE-HE···5M7-O18 | 3.0 | 141.5 | 77.1 | |
| Tyr131-OH-HH···5M7-O18 | 3.3 | 128.3 | 2.3 | |
| FABP4-65X | Arg126-NH2-HH21···65X-N28 | 2.9 | 153.4 | 99.7 |
| Arg126-NE-HE···65X-N28 | 3.1 | 138.2 | 65.4 | |
| Arg126-NH2-HH21···65X-N27 | 3.3 | 158.1 | 53.9 | |
| Arg126-NE-HE···65X-N27 | 3.3 | 150.0 | 34.1 | |
| Tyr128-OH-HH···65X-N26 | 3.2 | 155.5 | 46.4 | |
| Tyr128-OH-HH···65X-N27 | 2.9 | 158.2 | 98.0 | |
| Tyr128-OH-HH···65X-N28 | 3.2 | 138.8 | 57.1 | |
| FABP5-65X | Arg129-NH2-HH21···65X-N28 | 2.9 | 151.3 | 81.4 |
| Arg129-NE-HE···65X-N28 | 3.1 | 140.7 | 61.0 | |
| Arg129-NH2-HH21···65X-N27 | 3.3 | 154.9 | 50.0 | |
| Arg129-NE-HE···65X-N27 | 3.3 | 153.6 | 30.0 | |
| Tyr131-OH-HH···65X-N26 | 3.1 | 151.3 | 47.9 | |
| Tyr131-OH-HH···65X-N27 | 2.9 | 152.8 | 80.5 | |
| Tyr131-OH-HH···65X-N28 | 3.3 | 137.3 | 25.4 | |
| FABP4-65Z | Arg126-NH2-HH21···65Z-O21 | 2.8 | 157.7 | 99.9 |
| Arg126-NE-HE···65Z-O21 | 3.1 | 136.5 | 89.2 | |
| Tyr128-OH-HH···65Z-O21 | 3.2 | 129.6 | 6.1 | |
| FABP5-65Z | Arg129-NH2-HH21···65Z-O21 | 2.7 | 156.6 | 99.9 |
| Arg129-NE-HE···65Z-O21 | 3.1 | 138.4 | 82.7 | |
| Tyr131-OH-HH···65Z-O21 | 3.1 | 130.1 | 5.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, F.; Liu, X.; Zhang, S.; Su, J.; Zhang, Q.; Chen, J. Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5. Int. J. Mol. Sci. 2018, 19, 2496. https://doi.org/10.3390/ijms19092496
Yan F, Liu X, Zhang S, Su J, Zhang Q, Chen J. Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5. International Journal of Molecular Sciences. 2018; 19(9):2496. https://doi.org/10.3390/ijms19092496
Chicago/Turabian StyleYan, Fangfang, Xinguo Liu, Shaolong Zhang, Jing Su, Qinggang Zhang, and Jianzhong Chen. 2018. "Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5" International Journal of Molecular Sciences 19, no. 9: 2496. https://doi.org/10.3390/ijms19092496
APA StyleYan, F., Liu, X., Zhang, S., Su, J., Zhang, Q., & Chen, J. (2018). Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5. International Journal of Molecular Sciences, 19(9), 2496. https://doi.org/10.3390/ijms19092496