Mechanisms Underlying Spontaneous Action Potential Generation Induced by Catecholamine in Pulmonary Vein Cardiomyocytes: A Simulation Study
Abstract
:1. Introduction
2. Results
2.1. Intracellular Ca2+ Dynamics Revealed by Bifurcation Analyses
2.2. Absence of Automaticity Inherent in Plasma Membrane Ionic Channels in the PVC
2.3. Generation of APTDs and an Activation Threshold for Ca2+tot
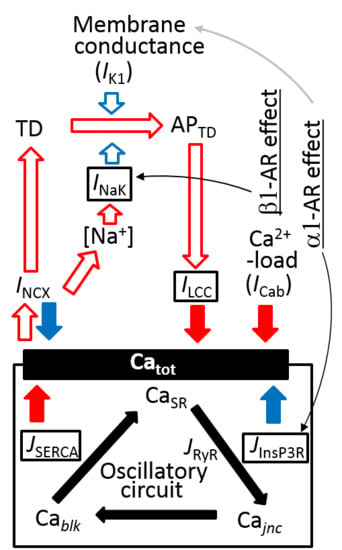
2.4. Separation of α1- and β1-AR Influences on Catot under Resting Condition
2.5. Marked Latency before the Onset of Repetitive APTD Generation after AR Stimulation
2.6. Involvement of the Spontaneous Membrane Fluctuations in Determining the Latency
2.7. Latency Histogram of the APTD Burst
3. Discussion
3.1. Brief Summary
3.2. Co-Localization of InsP3R with RyRs in the Sub-Sarcolemmal Space Supporting Spontaneous CICR
3.3. Peculiarity of APTD Generated in PVCs Compared to Aatrial and Ventricular Myocytes
3.4. Ca2+ Overload and β1-AR Stimulation Evoking Repetitive APTD Generation in PVCs
3.5. The Latency and Frequency of APTDs Under NA Effects
3.6. Coupling Several Layers of Physiological Mechanisms to Regulate Catot in PVCs
3.7. Limitations
4. Materials and Methods
4.1. Intracellular Ca2+ Compartments and Distribution of Ionic Channels and Transporters in the PVC Model
4.2. Relationship Between Local [Ca2+]nd and Spontaneous Ca2+ Release
4.3. Ion Channels and Transporters
4.4. Simulation of NA Stimulation of PVCs
4.4.1. Implementation of β1-AR Effects
4.4.2. Na+/K+ Pump
4.4.3. SERCA
4.4.4. LCC
4.4.5. α1-Adrenergic Signal, [IP3]
4.4.6. InsP3R
4.4.7. Background K+ Current, IKbg
4.5. Simulation of the Random Events of CICR
4.6. Changes in Membrane Potential and Ion Concentrations
4.7. Bifurcation Analysis on the Ca2+ Dynamics Within the Cell in the Absence of Membrane Ionic Fluxes
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| nd | Nano-domain |
| jnc | Junction space |
| iz | Intermediate zone |
| blk | Bulk space |
| SRup | Ca2+ uptake site of sarcoplasmic reticulum |
| SRrl | Ca2+ releasing site of sarcoplasmic reticulum |
| CaRU | Ca2+ releasing unit |
| couplon | A cluster of RyRs on SR membrane |
| Catot | Total Ca2+ content (femtomole) |
| Vm | Membrane potential (mV) |
| Cm | Membrane capacitance (pF) |
| TD | Transient membrane depolarization induced by spontaneous Ca2+ release through NCX activation |
| APTD | Action potential triggered by TD |
| CICR | Ca2+-induced Ca2+ release |
| NA | Noradrenaline |
| ISO | Isoprenaline |
| Abbreviation | Definition | Reference |
| INa | Transient component of sodium current | HuVEC model [16] |
| ICaL (LCC) | L-type calcium current | HuVEC model [16] |
| IKr | Delayed rectifier potassium current, fast component | HuVEC model [47] |
| IK1 | Inward rectifier potassium current | HuVEC model [16] |
| IKto | Transient outward potassium current | Pandit et al. [51] |
| IKur | Ultra-rapid outward potassium current | Bondarenko et al. [52] |
| IClh | Hyperpolarization activated chloride current | Experimental data by Okamoto et al. [8] |
| ICab, INab, IKb | Background currents for Ca2+, Na+ and K+ | Pandit et al. [51] |
| INCX | Na+/Ca2+ exchange current | HuVEC model [16] |
| INaK | Na+/K+ pump current | HuVEC model [16] |
| SERCA | Sarcoplasmic/endoplasmic reticulum calcium pump | HuVEC model [16] |
| InsP3R | Inositol (1,4,5)-trisphosphate receptor | Sneyd et al. [60] |
| RyR | Ryanodine receptor | HuVEC model [16] |
References
- Haissaguerre, M.; Jais, P.; Shah, D.C.; Takahashi, A.; Hocini, M.; Quiniou, G.; Garrigue, S.; Le Mouroux, A.; Le Metayer, P.; Clementy, J. Spontaneous initiation of atrial fibrillation by ectopic beats originating in the pulmonary veins. N. Engl. J. Med. 1998, 339, 659–666. [Google Scholar] [CrossRef] [PubMed]
- Maupoil, V.; Bronquard, C.; Freslon, J.L.; Cosnay, P.; Findlay, I. Ectopic activity in the rat pulmonary vein can arise from simultaneous activation of α—and β1—adrenoceptors. Br. J. Pharm. 2007, 150, 899–905. [Google Scholar] [CrossRef] [PubMed]
- Ehrlich, J.R.; Cha, T.J.; Zhang, L.; Chartier, D.; Melnyk, P.; Hohnloser, S.H.; Nattel, S. Cellular electrophysiology of canine pulmonary vein cardiomyocytes: Action potential and ionic current properties. J. Physiol. 2003, 551, 801–813. [Google Scholar] [CrossRef] [PubMed]
- Namekata, I.; Tsuneoka, Y.; Tanaka, H. Electrophysiological and pharmacological properties of the pulmonary vein myocardium. Biol. Pharm. Bull. 2013, 36, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Takahara, A.; Hagiwara, M.; Namekata, I.; Tanaka, H. Pulmonary Vein Myocardium as a Possible Pharmacological Target for the Treatment of Atrial Fibrillation. J. Pharm. Sci. 2014, 126, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Malecot, C.O.; Bredeloux, P.; Findlay, I.; Maupoil, V. A TTX-sensitive resting Na+ permeability contributes to the catecholaminergic automatic activity in rat pulmonary vein. J. Cardiovasc. Electrophysiol. 2015, 26, 311–319. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, Y.; Takano, M.; Ohba, T.; Ono, K. Arrhythmogenic coupling between the Na+-Ca2+ exchanger and inositol 1,4,5-triphosphate receptor in rat pulmonary vein cardiomyocytes. J. Mol. Cell Cardiol. 2012, 52, 988–997. [Google Scholar] [CrossRef]
- Okamoto, Y.; Kawamura, K.; Nakamura, Y.; Ono, K. Pathological impact of hyperpolarization-activated chloride current peculiar to rat pulmonary vein cardiomyocytes. J. Mol. Cell. Cardiol. 2014, 66, 53–62. [Google Scholar] [CrossRef]
- Doisne, N.; Maupoil, V.; Cosnay, P.; Findlay, I. Catecholaminergic automatic activity in the rat pulmonary vein: Electrophysiological differences between cardiac muscle in the left atrium and pulmonary vein. Am. J. Physiol. Heart. Circ. Physiol. 2009, 297, 102–108. [Google Scholar] [CrossRef]
- Lipp, P.; Laine, M.; Tovey, S.C.; Burrell, K.M.; Berridge, M.J.; Li, W.; Bootman, M.D. Functional InsP3 receptors that may modulate excitation-contraction coupling in the heart. Curr. Biol. 2000, 10, 939–942. [Google Scholar] [CrossRef]
- Mackenzie, L.; Bootman, M.D.; Laine, M.; Berridge, M.J.; Thuring, J.; Holmes, A.; Li, W.H.; Lipp, P. The role of inositol 1,4,5-trisphosphate receptors in Ca2+ signalling and the generation of arrhythmias in rat atrial myocytes. J. Physiol. 2002, 541, 395–409. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.; Spencer, B.D.; Adeniran, I.; Zhang, H. Development of biophysically detailed electrophysiological models for pacemaking and non-pacemaking human pulmonary vein cardiomyocytes. Conf Proc. IEEE Eng. Med. Biol. Soc. 2012, 2012, 199–202. [Google Scholar] [PubMed]
- Seol, C.A.; Kim, J.; Kim, W.T.; Ha, J.M.; Choe, H.; Jang, Y.J.; Shim, E.B.; Youm, J.B.; Earm, Y.E.; Leem, C.H. Simulation of spontaneous action potentials of cardiomyocytes in pulmonary veins of rabbits. Prog. Biophys. Mol. Biol. 2008, 96, 132–151. [Google Scholar] [CrossRef] [PubMed]
- Hinch, R. A mathematical analysis of the generation and termination of calcium sparks. Biophys. J. 2004, 86, 1293–1307. [Google Scholar] [CrossRef]
- Hinch, R.; Greenstein, J.L.; Tanskanen, A.J.; Xu, L.; Winslow, R.L. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys. J. 2004, 87, 3723–3736. [Google Scholar] [CrossRef] [PubMed]
- Himeno, Y.; Asakura, K.; Cha, C.Y.; Memida, H.; Powell, T.; Amano, A.; Noma, A. A human ventricular myocyte model with a refined representation of excitation-contraction coupling. Biophys. J. 2015, 109, 415–427. [Google Scholar] [CrossRef] [PubMed]
- Cooling, M.; Hunter, P.; Crampin, E.J. Modeling hypertrophic IP3 transients in the cardiac myocyte. Biophys. J. 2007, 93, 3421–3433. [Google Scholar] [CrossRef]
- Saucerman, J.J.; Brunton, L.L.; Michailova, A.P.; McCulloch, A.D. Modeling beta-adrenergic control of cardiac myocyte contractility in silico. J. Biol. Chem. 2003, 278, 47997–48003. [Google Scholar] [CrossRef] [PubMed]
- Ferrier, G.R. The effects of tension on acetylstrophanthidin-induced transient depolarizations and aftercontractions in canine myocardial and Purkinje tissues. Circ. Res. 1976, 38, 156–162. [Google Scholar] [CrossRef]
- Aronson, R.S.; Gelles, J.M. The effect of ouabain, dinitrophenol, and lithium on the pacemaker current in sheep cardiac Purkinje fibers. Circ. Res. 1977, 40, 517–524. [Google Scholar] [CrossRef]
- Kass, R.S.; Tsien, R.W.; Weingart, R. Ionic basis of transient inward current induced by strophanthidin in cardiac Purkinje fibres. J. Physiol. 1978, 281, 209–226. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, H.; Noma, A.; Kurachi, Y.; Irisawa, H. Transient depolarization and spontaneous voltage fluctuations in isolated single cells from guinea pig ventricles. Calcium-mediated membrane potential fluctuations. Circ. Res. 1982, 51, 142–151. [Google Scholar] [CrossRef]
- Ter Keurs, H.E.; Boyden, P.A. Calcium and arrhythmogenesis. Physiol. Rev. 2007, 87, 457–506. [Google Scholar] [CrossRef]
- Cha, C.Y.; Santos, E.; Amano, A.; Shimayoshi, T.; Noma, A. Time-dependent changes in membrane excitability during glucose-induced bursting activity in pancreatic beta cells. J. Gen. Physiol. 2011, 138, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Takeda, Y.; Shimayoshi, T.; Holz, G.G.; Noma, A. Modeling analysis of inositol 1,4,5-trisphosphate receptor-mediated Ca2+ mobilization under the control of glucagon-like peptide-1 in mouse pancreatic beta-cells. Am. J. Physiol. Cell. Physiol. 2016, 310, 337–347. [Google Scholar] [CrossRef]
- Kurata, Y.; Tsumoto, K.; Hayashi, K.; Hisatome, I.; Tanida, M.; Kuda, Y.; Shibamoto, T. Dynamical mechanisms of phase-2 early afterdepolarizations in human ventricular myocytes: Insights from bifurcation analyses of two mathematical models. Am. J. Physiol. Heart Circ. Physiol. 2017, 312, 106–127. [Google Scholar] [CrossRef] [PubMed]
- Shimoni, Y.; Severson, D.; Giles, W. Thyroid status and diabetes modulate regional differences in potassium currents in rat ventricle. J. Physiol. 1995, 488, 673–688. [Google Scholar] [CrossRef]
- Shinagawa, Y.; Satoh, H.; Noma, A. The sustained inward current and inward rectifier K+ current in pacemaker cells dissociated from rat sinoatrial node. J. Physiol. 2000, 523, 593–605. [Google Scholar] [CrossRef]
- Severs, N.J.; Slade, A.M.; Powell, T.; Twist, V.W.; Warren, R.L. Correlation of ultrastructure and function in calcium-tolerant myocytes isolated from the adult rat heart. J. Ultrastruct. Res. 1982, 81, 222–239. [Google Scholar] [CrossRef]
- Volders, P.G.; Vos, M.A.; Szabo, B.; Sipido, K.R.; de Groot, S.H.; Gorgels, A.P.; Wellens, H.J.; Lazzara, R. Progress in the understanding of cardiac early afterdepolarizations and torsades de pointes: Time to revise current concepts. Cardiovasc. Res. 2000, 46, 376–392. [Google Scholar] [CrossRef]
- Alfonzo-Mendez, M.A.; Carmona-Rosas, G.; Hernandez-Espinosa, D.A.; Romero-Avila, M.T.; Garcia-Sainz, J.A. Different phosphorylation patterns regulate alpha1D-adrenoceptor signaling and desensitization. Biochim. Biophys. Acta. Mol. Cell. Res. 2018, 1865, 842–854. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sainz, J.A.; Vazquez-Prado, J.; del Carmen Medina, L. Alpha 1-adrenoceptors: Function and phosphorylation. Eur. J. Pharm. 2000, 389, 1–12. [Google Scholar] [CrossRef]
- Rajagopal, S.; Shenoy, S.K. GPCR desensitization: Acute and prolonged phases. Cell. Signal 2018, 41, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Abdellatif, M.M.; Neubauer, C.F.; Lederer, W.J.; Rogers, T.B. Angiotensin-induced desensitization of the phosphoinositide pathway in cardiac cells occurs at the level of the receptor. Circ. Res. 1991, 69, 800–809. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Pak, E.; Zhang, H.L.; Kline, R.P.; Steinberg, S.F. Endothelin-dependent actions in cultured AT-1 cardiac myocytes. The role of the epsilon isoform of protein kinase C. Circ. Res. 1996, 78, 724–736. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Hiraoka, M.; Hirano, Y. Effects of alpha1-adrenergic stimulation on L-type Ca2+ current in rat ventricular myocytes. J. Mol. Cell. Cardiol. 1998, 30, 1955–1965. [Google Scholar] [CrossRef] [PubMed]
- Terzic, A.; Puceat, M.; Clement, O.; Scamps, F.; Vassort, G. Alpha 1-adrenergic effects on intracellular pH and calcium and on myofilaments in single rat cardiac cells. J. Physiol. 1992, 447, 275–292. [Google Scholar] [CrossRef]
- Miki, K.; Yoshimoto, M. Sympathetic nerve activity during sleep, exercise, and mental stress. Auton. Neurosci. 2013, 174, 15–20. [Google Scholar] [CrossRef]
- Hartmann, H.A.; Mazzocca, N.J.; Kleiman, R.B.; Houser, S.R. Effects of phenylephrine on calcium current and contractility of feline ventricular myocytes. Am. J. Physiol. 1988, 255, 1173–1180. [Google Scholar] [CrossRef]
- Hescheler, J.; Nawrath, H.; Tang, M.; Trautwein, W. Adrenoceptor-mediated changes of excitation and contraction in ventricular heart muscle from guinea-pigs and rabbits. J. Physiol. 1988, 397, 657–670. [Google Scholar] [CrossRef]
- Ertl, R.; Jahnel, U.; Nawrath, H.; Carmeliet, E.; Vereecke, J. Differential electrophysiologic and inotropic effects of phenylephrine in atrial and ventricular heart muscle preparations from rats. Naunyn. Schmiedebergs Arch. Pharm. 1991, 344, 574–581. [Google Scholar] [CrossRef]
- Jahnel, U.; Duwe, E.; Pfennigsdorf, S.; Nawrath, H. On the mechanism of action of phenylephrine in rat atrial heart muscle. Naunyn Schmiedebergs Arch. Pharm. 1994, 349, 408–415. [Google Scholar] [CrossRef]
- Schumann, H.J.; Wagner, J.; Knorr, A.; Reidemeister, J.C.; Sadony, V.; Schramm, G. Demonstration in human atrial preparations of alpha-adrenoceptors mediating positive inotropic effects. Naunyn Schmiedebergs Arch. Pharm. 1978, 302, 333–336. [Google Scholar] [CrossRef]
- Skomedal, T.; Aass, H.; Osnes, J.B.; Fjeld, N.B.; Klingen, G.; Langslet, A.; Semb, G. Demonstration of an alpha adrenoceptor-mediated inotropic effect of norepinephrine in human atria. J. Pharm. Exp. 1985, 233, 441–446. [Google Scholar]
- Wang, Y.G.; Dedkova, E.N.; Ji, X.; Blatter, L.A.; Lipsius, S.L. Phenylephrine acts via IP3-dependent intracellular NO release to stimulate L-type Ca2+ current in cat atrial myocytes. J. Physiol 2005, 567, 143–157. [Google Scholar] [CrossRef] [PubMed]
- Jahnel, U.; Jakob, H.; Nawrath, H. Electrophysiologic and inotropic effects of alpha-adrenoceptor stimulation in human isolated atrial heart muscle. Naunyn Schmiedebergs Arch. Pharm. 1992, 346, 82–87. [Google Scholar] [CrossRef]
- Asakura, K.; Cha, C.Y.; Yamaoka, H.; Horikawa, Y.; Memida, H.; Powell, T.; Amano, A.; Noma, A. EAD and DAD mechanisms analyzed by developing a new human ventricular cell model. Prog. Biophys. Mol. Biol. 2014, 116, 11–24. [Google Scholar] [CrossRef]
- Song, Y.; Hao, G.; Boyett, M.; Yang, X.; Du, Y.; Shui, Z. Action potential, sodium and gap junction channels in rat pulmonary vein myocytes. Proc. Physiol. Soc. 2009, 15. [Google Scholar]
- Boyle, W.A.; Nerbonne, J.M. Two functionally distinct 4-aminopyridine-sensitive outward K+ currents in rat atrial myocytes. J. Gen. Physiol. 1992, 100, 1041–1067. [Google Scholar] [CrossRef]
- Pond, A.L.; Scheve, B.K.; Benedict, A.T.; Petrecca, K.; Van Wagoner, D.R.; Shrier, A.; Nerbonne, J.M. Expression of distinct ERG proteins in rat, mouse, and human heart. Relation to functional IKr channels. J. Biol. Chem. 2000, 275, 5997–6006. [Google Scholar] [CrossRef]
- Pandit, S.V.; Clark, R.B.; Giles, W.R.; Demir, S.S. A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys. J. 2001, 81, 3029–3051. [Google Scholar] [CrossRef]
- Bondarenko, V.E.; Szigeti, G.P.; Bett, G.C.; Kim, S.J.; Rasmusson, R.L. Computer model of action potential of mouse ventricular myocytes. Am. J. Physiol. Heart Circ. Physiol. 2004, 287, 1378–1403. [Google Scholar] [CrossRef] [PubMed]
- Kuzumoto, M.; Takeuchi, A.; Nakai, H.; Oka, C.; Noma, A.; Matsuoka, S. Simulation analysis of intracellular Na+ and Cl− homeostasis during β1-adrenergic stimulation of cardiac myocyte. Prog. Biophys. Mol. Biol. 2008, 96, 171–186. [Google Scholar] [CrossRef] [PubMed]
- Himeno, Y.; Sarai, N.; Matsuoka, S.; Noma, A. Ionic mechanisms underlying the positive chronotropy induced by beta1-adrenergic stimulation in guinea pig sinoatrial node cells: A simulation study. J. Physiol. Sci. 2008, 58, 53–65. [Google Scholar] [CrossRef]
- Oka, C.; Cha, C.Y.; Noma, A. Characterization of the cardiac Na+/K+ pump by development of a comprehensive and mechanistic model. J. Biol. 2010, 265, 68–77. [Google Scholar] [CrossRef] [PubMed]
- Smith, N.P.; Crampin, E.J. Development of models of active ion transport for whole-cell modelling: Cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 2004, 85, 387–405. [Google Scholar] [CrossRef] [PubMed]
- Despa, S.; Bossuyt, J.; Han, F.; Ginsburg, K.S.; Jia, L.G.; Kutchai, H.; Tucker, A.L.; Bers, D.M. Phospholemman-phosphorylation mediates the beta-adrenergic effects on Na/K pump function in cardiac myocytes. Circ. Res. 2005, 97, 252–259. [Google Scholar] [CrossRef]
- Tran, K.; Smith, N.P.; Loiselle, D.S.; Crampin, E.J. A thermodynamic model of the cardiac sarcoplasmic/endoplasmic Ca2+ (SERCA) pump. Biophys. J. 2009, 96, 2029–2042. [Google Scholar] [CrossRef]
- Miyakawa, T.; Maeda, A.; Yamazawa, T.; Hirose, K.; Kurosaki, T.; Iino, M. Encoding of Ca2+ signals by differential expression of IP3 receptor subtypes. EMBO J. 1999, 18, 1303–1308. [Google Scholar] [CrossRef]
- Sneyd, J.; Dufour, J.F. A dynamic model of the type-2 inositol trisphosphate receptor. Proc. Natl. Acad. Sci. USA 2002, 99, 2398–2403. [Google Scholar] [CrossRef] [Green Version]
- Jahnel, U.; Nawrath, H.; Carmeliet, E.; Vereecke, J. Depolarization-induced influx of sodium in response to phenylephrine in rat atrial heart muscle. J. Physiol. 1991, 432, 621–637. [Google Scholar] [CrossRef] [PubMed]
- Ermentrout, B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. Software. Environments and Tools; Society for Industrial and Applied Mathematics SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Yan, D.H.; Ishihara, K. Two Kir2.1 channel populations with different sensitivities to Mg2+ and polyamine block: A model for the cardiac strong inward rectifier K+ channel. J. Physiol. 2005, 563, 725–744. [Google Scholar] [CrossRef] [PubMed]







| Channels and Transporters | jnc | iz | blk |
|---|---|---|---|
| Ca2+ insensitive channels (INa, IKr, IK1, IKto, IKur, IClh, IKbg, INabg) | - | 0.1 | 0.9 |
| IPMCA | - | 0.1 | 0.9 |
| INaK | - | 0.1 | 0.9 |
| ICaL(LCC) | 0.75 | 0.15 | 0.1 |
| INCX | 0.03 | 0.25 | 0.72 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umehara, S.; Tan, X.; Okamoto, Y.; Ono, K.; Noma, A.; Amano, A.; Himeno, Y. Mechanisms Underlying Spontaneous Action Potential Generation Induced by Catecholamine in Pulmonary Vein Cardiomyocytes: A Simulation Study. Int. J. Mol. Sci. 2019, 20, 2913. https://doi.org/10.3390/ijms20122913
Umehara S, Tan X, Okamoto Y, Ono K, Noma A, Amano A, Himeno Y. Mechanisms Underlying Spontaneous Action Potential Generation Induced by Catecholamine in Pulmonary Vein Cardiomyocytes: A Simulation Study. International Journal of Molecular Sciences. 2019; 20(12):2913. https://doi.org/10.3390/ijms20122913
Chicago/Turabian StyleUmehara, Shohei, Xiaoqiu Tan, Yosuke Okamoto, Kyoichi Ono, Akinori Noma, Akira Amano, and Yukiko Himeno. 2019. "Mechanisms Underlying Spontaneous Action Potential Generation Induced by Catecholamine in Pulmonary Vein Cardiomyocytes: A Simulation Study" International Journal of Molecular Sciences 20, no. 12: 2913. https://doi.org/10.3390/ijms20122913
APA StyleUmehara, S., Tan, X., Okamoto, Y., Ono, K., Noma, A., Amano, A., & Himeno, Y. (2019). Mechanisms Underlying Spontaneous Action Potential Generation Induced by Catecholamine in Pulmonary Vein Cardiomyocytes: A Simulation Study. International Journal of Molecular Sciences, 20(12), 2913. https://doi.org/10.3390/ijms20122913