Behavior of Embedded Cation-Exchange Particles in a DC Electric Field
Abstract
:1. Introduction
2. Results
2.1. Studied Membranes—Current–Voltage Curves
2.1.1. One-Particle System
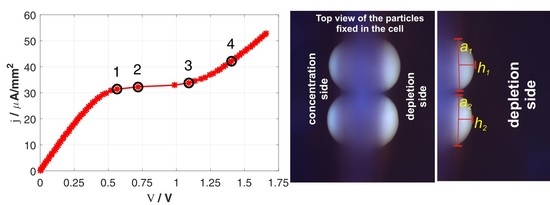
2.1.2. Two-Particle System
2.1.3. Three-Particle System
2.1.4. Four-Particle System
2.2. pH Changes at Studied Systems
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Electrochemical Cell
4.3. Ion-Exchange Surface Area
4.4. Experimental Set-Up
4.5. Measurements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CVC | Current–voltage curve |
| DC | Direct current |
References
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Alvarado, L.; Chen, A.C. Electrodeionization: Principles, strategies and applications. Electrochim. Acta 2014, 132, 583–597. [Google Scholar] [CrossRef]
- Strathmann, H.; Grabowski, A.; Eigenberger, G. Ion-exchange membranes in the chemical process industry. Ind Eng Chem. Res. 2013, 52, 10364–10379. [Google Scholar] [CrossRef]
- Slouka, Z.; Senapati, S.; Chang, H.C. Microfluidic systems with ion-selective membranes. Annu. Rev. Anal. Chem. 2014, 7, 317–335. [Google Scholar] [CrossRef] [PubMed]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B.; Nikonenko, V.V.; Zabolotsky, V.I. Ion transfer in membrane and ion exchange materials. Usp Khim 2003, 72, 438–470. [Google Scholar] [CrossRef]
- Nagarale, R.K.; Gohil, G.S.; Shahi, V.K. Recent developments on ion-exchange membranes and electro-membrane processes. Adv Colloid. Interfac. 2006, 119, 97–130. [Google Scholar] [CrossRef] [PubMed]
- Vobecka, L.; Svoboda, M.; Benes, J.; Bellon, T.; Slouka, Z. Heterogeneity of heterogeneous ion-exchange membranes investigated by chronopotentiometry and x-ray computed microtomography. J. Membr. Sci. 2018, 559, 127–137. [Google Scholar] [CrossRef]
- Svoboda, M.; Benes, J.; Vobecka, L.; Slouka, Z. Swelling induced structural changes of a heterogeneous cation-exchange membrane analyzed by micro-computed tomography. J. Membr. Sci. 2017, 525, 195–201. [Google Scholar] [CrossRef]
- Marti-Calatayud, M.C.; Buzzi, D.C.; Garcia-Gabaldon, M.; Bernardes, A.M.; Tenorio, J.A.S.; Perez-Herranz, V. Ion transport through homogeneous and heterogeneous ion-exchange membranes in single salt and multicomponent electrolyte solutions. J. Membr. Sci. 2014, 466, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Krol, J.J.; Wessling, M.; Strathmann, H. Concentration polarization with monopolar ion exchange membranes: Current-voltage curves and water dissociation. J. Membr. Sci. 1999, 162, 145–154. [Google Scholar] [CrossRef]
- Svoboda, M.; Slouka, Z.; Schrott, W.; Snita, D. Cation exchange membrane integrated into a microfluidic device. Microelectron Eng. 2009, 86, 1371–1374. [Google Scholar] [CrossRef]
- Maletzki, F.; Rosler, H.W.; Staude, E. Ion transfer across electrodialysis membranes in the overlimiting current range - stationary voltage current characteristics and current noise power spectra under different conditions of free-convection. J. Membr. Sci. 1992, 71, 105–115. [Google Scholar] [CrossRef]
- Belloň, T.; Polezhaev, P.; Vobecká, L.; Svoboda, M.; Slouka, Z. Experimental observation of phenomena developing on ion-exchange systems during current-voltage curve measurement. J. Membr. Sci. 2019, 572, 607–618. [Google Scholar] [CrossRef]
- Tanaka, Y. Concentration polarization in ion-exchange membrane electrodialysis. J. Membr. Sci. 1991, 57, 217–235. [Google Scholar] [CrossRef]
- Tanaka, Y. Concentration polarization in ion-exchange membrane electrodialysis - the events arising in a flowing solution in a desalting cell. J. Membr. Sci. 2003, 216, 149–164. [Google Scholar] [CrossRef]
- Tanaka, Y. Concentration polarization in ion-exchange membrane electrodialysis - the events arising in an unforced flowing solution in a desalting cell. J. Membr. Sci. 2004, 244, 1–16. [Google Scholar] [CrossRef]
- Rosler, H.W.; Maletzki, F.; Staude, E. Ion transfer across electrodialysis membranes in the overlimiting current range - chronopotentiometric studies. J. Membr. Sci. 1992, 72, 171–179. [Google Scholar] [CrossRef]
- Dydek, E.V.; Zaltzman, B.; Rubinstein, I.; Deng, D.S.; Mani, A.; Bazant, M.Z. Overlimiting current in a microchannel. Phys. Rev. Lett. 2011, 107, 118301. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Balster, J.; Yildirim, M.H.; Stamatialis, D.F.; Ibanez, R.; Lammertink, R.G.H.; Jordan, V.; Wessling, M. Morphology and microtopology of cation-exchange polymers and the origin of the overlimiting current. J. Phys. Chem. B 2007, 111, 2152–2165. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Nikonenko, V.V.; Urtenov, M.K.; Lebedev, K.A.; Bugakov, V.V. Electroconvection in systems with heterogeneous ion-exchange membranes. Russ. J. Electrochem. 2012, 48, 692–703. [Google Scholar] [CrossRef]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. Effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458–13469. [Google Scholar] [CrossRef] [PubMed]
- Simons, R. Water splitting in ion-exchange membranes. Electrochim. Acta 1985, 30, 275–282. [Google Scholar] [CrossRef]
- Belova, E.; Lopatkova, G.; Pismenskaya, N.; Nikonenko, V.; Larchet, C. Role of water splitting in development in ion-exchange membrane of electroconvection systems. Desalination 2006, 199, 59–61. [Google Scholar] [CrossRef]
- Slouka, Z.; Senapati, S.; Yan, Y.; Chang, H.C. Charge inversion, water splitting, and vortex suppression due to DNA sorption on ion-selective membranes and their ion-current signatures. Langmuir 2013, 29, 8275–8283. [Google Scholar] [CrossRef]
- Sablani, S.S.; Goosen, M.F.A.; Al-Belushi, R.; Wilf, M. Concentration polarization in ultrafiltration and reverse osmosis: A critical review. Desalination 2001, 141, 269–289. [Google Scholar] [CrossRef]
- Roghmans, F.; Evdochenko, E.; Stockmeier, F.; Schneider, S.; Smailji, A.; Tiwari, R.; Mikosch, A.; Karatay, E.; Kuhne, A.; Walther, A.; et al. 2D patterned ion-exchange membranes induce electroconvection. Adv. Mater. Interfaces 2019, 6, 1801309. [Google Scholar] [CrossRef]
- Davidson, S.M.; Wessling, M.; Mani, A. On the dynamical regimes of pattern-accelerated electroconvection. Sci. Rep. 2016, 6, 22505. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Akberova, E.M.; Zabolotskii, V.I. Electroconvection in systems with heterogeneous ion-exchange membranes after thermal modification. Russ. J. Electrochem. 2017, 53, 398–410. [Google Scholar] [CrossRef]
- Butylskii, D.Y.; Mareev, S.A.; Pismenskaya, N.D.; Apel, P.Y.; Polezhaeva, O.A.; Nikonenko, V.V. Phenomenon of two transition times in chronopotentiometry of electrically inhomogeneous ion exchange membranes. Electrochim. Acta 2018, 273, 289–299. [Google Scholar] [CrossRef]
- Green, Y.; Park, S.; Yossifon, G. Bridging the gap between an isolated nanochannel and a communicating multipore heterogeneous membrane. Phys. Rev. E 2015, 91, 011002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mareev, S.A.; Nebavskiy, A.V.; Nichka, V.S.; Urtenov, M.K.; Nikonenko, V.V. The nature of two transition times on chronopotentiograms of heterogeneous ion exchange membranes: 2d modelling. J. Membr. Sci. 2019, 575, 179–190. [Google Scholar] [CrossRef]
- Nikonenko, V.; Nebavsky, A.; Mareev, S.; Kovalenko, A.; Urtenov, M.; Pourcelly, G. Modelling of ion transport in electromembrane systems: Impacts of membrane bulk and surface heterogeneity. Appl. Sci. 2019, 9, 25. [Google Scholar] [CrossRef]
- Belloň, T.; Polezhaev, P.; Vobecká, T.; Slouka, Z. Fouling of a heterogeneous anion-exchange membrane and single anion-exchange resin particle by ssdna manifests differently. J. Membr. Sci. 2019, 572, 619–631. [Google Scholar] [CrossRef]







| Membrane | Particle Surfaces | Overall Surface/mm2 | Limiting Current Density/A/m2 | Slope of Underlimiting Region/A/m2/V | Slope of Overlimiting Region/A/m2/V |
|---|---|---|---|---|---|
| One-particle membrane | S1 = 0.52 mm2 | 0.52 | 38.4 | 72.7 | 60.5 |
| Two-particle membrane | S1 = 0.63 mm2 S2 = 0.67 mm2 | 1.3 | 31.4 | 73 | 43.6 |
| Three-particle membrane | S1 = 0.49 mm2 S2 = 0.50 mm2 S3 = 0.51 mm2 | 1.5 | 34.7 | 41 | 33.2 |
| Four-particle membrane | S1 = 0.29 mm2 S2 = 0.20 mm2 S3 = 0.26 mm2 S3 = 0.28 mm2 | 1.03 | 40 | 64.4 | 44.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vobecká, L.; Belloň, T.; Slouka, Z. Behavior of Embedded Cation-Exchange Particles in a DC Electric Field. Int. J. Mol. Sci. 2019, 20, 3579. https://doi.org/10.3390/ijms20143579
Vobecká L, Belloň T, Slouka Z. Behavior of Embedded Cation-Exchange Particles in a DC Electric Field. International Journal of Molecular Sciences. 2019; 20(14):3579. https://doi.org/10.3390/ijms20143579
Chicago/Turabian StyleVobecká, Lucie, Tomáš Belloň, and Zdeněk Slouka. 2019. "Behavior of Embedded Cation-Exchange Particles in a DC Electric Field" International Journal of Molecular Sciences 20, no. 14: 3579. https://doi.org/10.3390/ijms20143579
APA StyleVobecká, L., Belloň, T., & Slouka, Z. (2019). Behavior of Embedded Cation-Exchange Particles in a DC Electric Field. International Journal of Molecular Sciences, 20(14), 3579. https://doi.org/10.3390/ijms20143579