Partial Fluxes of Phosphoric Acid Anions through Anion-Exchange Membranes in the Course of NaH2PO4 Solution Electrodialysis
Abstract
:1. Introduction
2. Results and Discussion
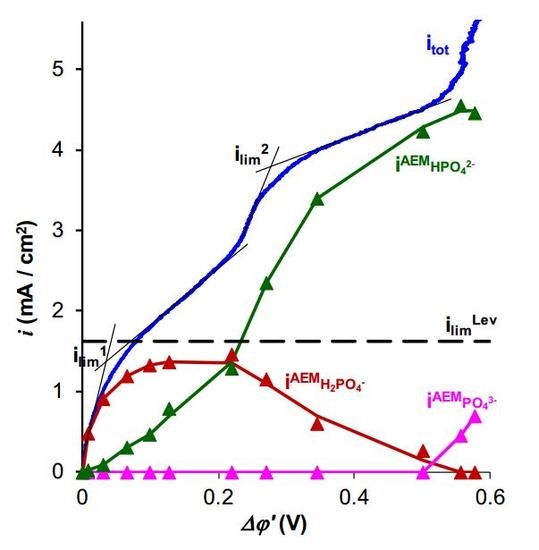
2.1. Total and Partial Current–Voltage Characteristics
2.1.1. Contributions of Electroconvection and Exaltation Effects.
2.1.2. Rate of Phosphorus Removal from Feed Solution and Its Theoretical Assessment.
3. Materials and Methods
3.1. Membrane and Solutions
3.2. Methods
3.2.1. Effective Transport Numbers, Ti
3.2.2. Visualization of Electroconvective Vortices.
4. Theory
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paltrinieri, L.; Huerta, E.; Puts, T.; Van Baak, W.; Verver, A.B.; Sudhölter, E.J.R.; De Smet, L.C.P.M. Functionalized anion-exchange membranes facilitate electrodialysis of citrate and phosphate from model dairy wastewater. Environ. Sci. Technol. 2019, 53, 2396–2404. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Xie, S.; Hu, Z.; Wu, G.; Morrison, L.; Croot, P.; Hu, H.; Zhan, X. Nutrient recovery from pig manure digestate using electrodialysis reversal: Membrane fouling and feasibility of long-term operation. J. Membr. Sci. 2019, 573, 560–569. [Google Scholar] [CrossRef]
- Tran, A.T.K.; Zhang, Y.; Lin, J.; Mondal, P.; Ye, W.; Meesschaert, B.; Pinoy, L.; Van Der Bruggen, B. Phosphate pre-concentration from municipal wastewater by selectrodialysis: Effect of competing components. Sep. Purif. Technol. 2015, 141, 38–47. [Google Scholar] [CrossRef]
- Zhang, Y.; Desmidt, E.; Van Looveren, A.; Pinoy, L.; Meesschaert, B.; Van Der Bruggen, B. Phosphate separation and recovery from wastewater by novel electrodialysis. Environ. Sci. Technol. 2013, 47, 5888–5895. [Google Scholar] [CrossRef] [PubMed]
- Handojo, L.; Wardani, A.K.; Regina, D.; Bella, C.; Kresnowati, M.T.A.P.; Wenten, I.G. Electro-membrane processes for organic acid recovery. RSC Adv. 2019, 9, 7854–7869. [Google Scholar] [CrossRef] [Green Version]
- El Rayess, Y.; Mietton-Peuchot, M. Membrane technologies in wine industry: An overview. Crit. Rev. Food Sci. 2016, 56, 2005–2020. [Google Scholar] [CrossRef] [PubMed]
- Martín, J.; Díaz-Montaña, E.J.; Asuero, A.G. Recovery of anthocyanins using membrane technologies: A review. Crit. Rev. Anal. Chem. 2018, 48, 143–175. [Google Scholar] [CrossRef] [PubMed]
- Galier, S.; Roux-de Balmann, H. The electrophoretic membrane contactor: A mass transfer-based methodology applied to the separation of whey proteins. Sep. Purif. Technol. 2011, 77, 237–244. [Google Scholar] [CrossRef]
- Durand, R.; Fraboulet, E.; Marette, A.; Bazinet, L. Simultaneous double cationic and anionic molecule separation from herring milt hydrolysate and impact on resulting fraction bioactivities. Sep. Purif. Technol. 2019, 210, 431–441. [Google Scholar] [CrossRef]
- Chandra, A.; Tadimeti, J.G.D.; Chattopadhyay, S. Transport hindrances with electrodialytic recovery of citric acid from solution of strong electrolytes. Chin. J. Chem. Eng. 2018, 26, 278–292. [Google Scholar] [CrossRef]
- Suwal, S.; Rozoy, É.; Manenda, M.; Doyen, A.; Bazinet, L. Comparative study of in situ and ex situ enzymatic hydrolysis of milk protein and separation of bioactive peptides in an electromembrane reactor. ACS Sustain. Chem. Eng. 2017, 5, 5330–5340. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Fidaleo, M.; Moresi, M. Concentration of trisodium citrate by electrodialysis. J. Membr. Sci. 2013, 447, 376–386. [Google Scholar] [CrossRef]
- Myles, T.D.; Grew, K.N.; Peracchio, A.A.; Chiu, W.K.S. Transient ion exchange of anion exchange membranes exposed to carbon dioxide. J. Power Sour. 2015, 296, 225–236. [Google Scholar] [CrossRef]
- Ramirez, P.; Alcaraz, A.; Mafe, S.; Pellicer, J. pH and supporting electrolyte concentration effects on the passive transport of cationic and anionic drugs through fixed charge membranes. J. Membr. Sci. 1999, 161, 143–155. [Google Scholar] [CrossRef]
- Sarapulova, V.; Nevakshenova, E.; Pismenskaya, N.; Dammak, L.; Nikonenko, V. Unusual concentration dependence of ion-exchange membrane conductivity in ampholyte-containing solutions: Effect of ampholyte nature. J. Membr. Sci. 2015, 479, 28–38. [Google Scholar] [CrossRef]
- Andersen, M.B.; Rogers, D.M.; Mai, J.; Schudel, B.; Hatch, A.V.; Rempe, S.B.; Mani, A. Spatiotemporal pH dynamics in concentration polarization near ion-selective membranes. Langmuir 2014, 30, 7902–7912. [Google Scholar] [CrossRef]
- Femmer, R.; Mani, A.; Wessling, M. Ion transport through electrolyte/polyelectrolyte multi-layers. Sci. Rep. 2015, 5, 1–12. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Gnusin, N.P.; El’nikova, L.F.; Blednykh, V.M. Exhaustive purification of amino acids by removal of mineral impurities by electrodialysis with ion-exchange membranes. J. App. Chem.-Ussr 1986, 59, 127–131. [Google Scholar]
- Shaposhnik, V.A.; Eliseeva, T.V. Barrier effect during the electrodialysis of ampholytes. J. Membr. Sci. 1999, 161, 223–229. [Google Scholar] [CrossRef]
- Eliseeva, T.V.; Shaposhnik, V.A. Effects of circulation and facilitated electromigration of amino acids in electrodialysis with ion-exchange membranes. Russ. J. Electrochem. 2000, 36, 64–67. [Google Scholar] [CrossRef]
- Dufton, G.; Mikhaylin, S.; Gaaloul, S.; Bazinet, L. How electrodialysis configuration influences acid whey deacidification and membrane scaling. J. Dairy Sci. 2018, 101, 7833–7850. [Google Scholar] [CrossRef] [PubMed]
- Rotta, E.H.; Bitencourt, C.S.; Marder, L.; Bernardes, A.M. Phosphorus recovery from low phosphate-containing solution by electrodialysis. J. Membr. Sci. 2019, 573, 293–300. [Google Scholar] [CrossRef]
- Franck-Lacaze, L.; Sistat, P.; Huguet, P.; Lapicque, F. Protonation and diffusion phenomena in poly(4-vinylpyridine)-based weak anion-exchange membranes. J. Membr. Sci. 2009, 340, 257–265. [Google Scholar] [CrossRef]
- Koter, S.; Kultys, M. Modeling the electric transport of sulfuric and phosphoric acids through anion-exchange membranes. Sep. Purif. Technol. 2010, 73, 219–229. [Google Scholar] [CrossRef]
- Kozmai, A.E.; Nikonenko, V.V.; Zyryanova, S.; Pismenskaya, N.D.; Dammak, L. A simple model for the response of an anion-exchange membrane to variation in concentration and pH of bathing solution. J. Membr. Sci. 2018, 567, 127–138. [Google Scholar] [CrossRef]
- Vasil’eva, V.; Goleva, E.; Pismenskaya, N.; Kozmai, A.; Nikonenko, V. Effect of surface profiling of a cation-exchange membrane on the phenylalanine and NaCl separation performances in diffusion dialysis. Sep. Purif. Technol. 2019, 210, 48–59. [Google Scholar] [CrossRef]
- Ueno, K.; Doi, T.; Nanzai, B.; Igawa, M. Selective transport of neutral amino acids across a double-membrane system comprising cation and anion exchange membranes. J. Membr. Sci. 2017, 537, 344–352. [Google Scholar] [CrossRef]
- Ramírez, P.; Alcaraz, A.; Mafé, S. Modeling of amino acid electrodiffusion through fixed charge membranes. J. Coll. Interface Sci. 2001, 242, 164–173. [Google Scholar] [CrossRef]
- Rybalkina, O.A.; Tsygurina, K.A.; Melnikova, E.D.; Pourcelly, G.; Nikonenko, V.V.; Pismenskaya, N.D. Catalytic effect of ammonia-containing species on water splitting during electrodialysis with ion-exchange membranes. Electrochim. Acta 2019, 299, 946–962. [Google Scholar] [CrossRef]
- Belashova, E.D.; Pismenskaya, N.D.; Nikonenko, V.V.; Sistat, P.; Pourcelly, G. Current-voltage characteristic of anion-exchange membrane in monosodium phosphate solution. Modelling and experiment. J. Membr. Sci. 2017, 542, 177–185. [Google Scholar] [CrossRef]
- Melnikova, E.D.; Pismenskaya, N.D.; Bazinet, L.; Mikhaylin, S.; Nikonenko, V.V. Effect of ampholyte nature on current-voltage characteristic of anion-exchange membrane. Electrochim. Acta 2018, 285, 185–191. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Wang, Y.; Du, Y.; Feng, H.; Xu, T. Simultaneous recovery of ammonium and phosphorus via the integration of electrodialysis with struvite reactor. J. Membr. Sci. 2015, 490, 65–71. [Google Scholar] [CrossRef]
- Ward, A.J.; Arola, K.; Thompson Brewster, E.; Mehta, C.M.; Batstone, D.J. Nutrient recovery from wastewater through pilot scale electrodialysis. Water Res. 2018, 135, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Lin, L.; Tse, L.K.; Dong, H.; Yu, S.; Hoffmann, M.R. Membrane-separated electrochemical latrine wastewater treatment. Environ. Sci. Water Res. Technol. 2019, 5, 51–59. [Google Scholar] [CrossRef]
- Shi, L.; Hu, Y.; Xie, S.; Wu, G.; Hu, Z.; Zhan, X. Recovery of nutrients and volatile fatty acids from pig manure hydrolysate using two-stage bipolar membrane electrodialysis. Chem. Eng. J. 2018, 334, 134–142. [Google Scholar] [CrossRef]
- Ebbers, B.; Ottosen, L.M.; Jensen, P.E. Electrodialytic treatment of municipal wastewater and sludge for the removal of heavy metals and recovery of phosphorus. Electrochim. Acta 2015, 181, 90–99. [Google Scholar] [CrossRef]
- Geng, Y.-K.; Wang, Y.; Pan, X.-R.; Sheng, G.-P. Electricity generation and in situ phosphate recovery from enhanced biological phosphorus removal sludge by electrodialysis membrane bioreactor. Bioresour. Technol. 2018, 247, 471–476. [Google Scholar] [CrossRef]
- De Paepe, J.; Lindeboom, R.E.F.; Vanoppen, M.; De Paepe, K.; Demey, D.; Coessens, W.; Lamaze, S.; Verliefde, A.R.D.; Clauwaert, P.; Vlaeminck, S.E. Refinery and concentration of nutrients from urine with electrodialysis enabled by upstream precipitation and nitrification. Water Res. 2018, 144, 76–86. [Google Scholar] [CrossRef]
- Gallya, C.R.; Benvenutia, T.; Trindade, C.M.; Rodrigues, M.A.S.; Zoppas-Ferreira, J.; Pérez-Herranz, V.; Bernardes, A.M. Electrodialysis for the tertiary treatment of municipal wastewater: Efficiency of ion removal and ageing of ion exchange membranes. J. Environ. Chem. Eng. 2018, 3, 5855–5869. [Google Scholar] [CrossRef]
- Weinertova, K.; Honorato, R.S.; Stranska, E.; Nedela, D. Comparison of heterogeneous anion-exchanges for nitrate ion removal from mixed salt solution. Chem. Pap. 2018, 72, 469–478. [Google Scholar] [CrossRef]
- Paltrinieri, L.; Poltorak, L.; Chu, L.; Puts, T.; van Baak, W.; Sudhölter, E.J.R.; de Smet, L.C.P.M. Hybrid polyelectrolyte-anion exchange membrane and its interaction with phosphate. React. Funct. Polym. 2018, 133, 126–135. [Google Scholar] [CrossRef]
- Cowan, D.Q.; Brown, I.W. Effect of turbulence in limiting current in electrodialysis cell. Ind. Eng. Chem. 1959, 51, 1445–1449. [Google Scholar] [CrossRef]
- Chandra, A.; Tadimeti, J.G.D.; Bhuvanesh, E.; Pathiwada, D.; Chattopadhyay, S. Switching selectivity of carboxylic acids and associated physic-chemical changes with pH during electrodialysis of ternary mixtures. Sep. Purif. Technol. 2018, 193, 327–344. [Google Scholar] [CrossRef]
- Lopatkova, G.Y.; Volodina, E.I.; Pis’menskaya, N.D.; Fedotov, Y.A.; Cot, D.; Nikonenko, V.V. Effect of chemical modification of ion-exchange membrane MA-40 on its electrochemical characteristics. Russ. J. Electrochem. 2006, 42, 847–854. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Bugakov, V.V.; Sharafan, M.V.; Chermit, R.K. Transfer of electrolyte ions and water dissociation in anion-exchange membranes under intense current conditions. Russ. J. Electrochem. 2012, 48, 650–659. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Pokhidnia, E.V.; Pourcelly, G.; Nikonenko, V.V. Can the electrochemical performance of heterogeneous ion-exchange membranes be better than that of homogeneous membranes? J. Membr. Sci. 2018, 566, 54–68. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Equilibrium electro-osmotic instability in concentration polarization at a perfectly charge-selective interface. Phys. Rev. Fluids 2017, 2, 093702. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nikonenko, V.V.; Belova, E.I.; Lopatkova, G.Y.; Sistat, P.; Pourcelly, G.; Larshe, K. Coupled convection of solution near the surface of ion exchange membranes in intensive current regimes. Russ. J. Electrochem. 2007, 43, 307–327. [Google Scholar] [CrossRef]
- Kniaginicheva, E.; Pismenskaya, N.; Melnikov, S.; Belashova, E.; Sistat, P.; Cretin, M.; Nikonenko, V. Water splitting at an anion-exchange membrane as studied by impedance spectroscopy. J. Membr. Sci. 2015, 496, 78–83. [Google Scholar] [CrossRef]
- Kharkats, Y.I. The mechanism of supralimiting currents at ion-exchange membrane electrolyte interfaces. Sov. Electrochem. 1985, 21, 917–920. [Google Scholar]
- Urtenov, M.; Kirillova, E.; Seidova, N.; Nikonenko, V. Decoupling of the Nernst-Planck and Poisson equations. Application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007, 111, 14208–14222. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis. Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Rybalkina, O.A.; Melnikova, E.D.; Pismenskiy, A.V. Influence of gravitational convection on current–voltage characteristics of an electromembrane stack in sodium dihydrogen phosphate solution. Petrol. Chem. 2018, 58, 114–120. [Google Scholar] [CrossRef]
- Rubinstein, S.M.; Manukyan, G.; Staicu, A.; Rubinstein, I.; Zaltzman, B.; Lammertink, R.G.H.; Mugele, F.; Wessling, M. Direct observation of a nonequilibrium electro-osmotic instability. Phys. Rev. Lett. 2008, 101, 236101. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. Adv. Coll. Interface Sci. 2010, 160, 16. [Google Scholar] [CrossRef]
- Simons, R. Electric field effects on proton transfer between ionizable groups and water in ion exchange membranes. Electrochim. Acta 1984, 29, 151–158. [Google Scholar] [CrossRef]
- Simons, R. Strong electric field effects on proton transfer between membrane-bound amines and water. Nature 1979, 280, 824–826. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel’deshov, N.V.; Gnusin, N.P. Dissociation of water molecules in systems with ion-exchange membranes. Russ. Chem. Rev. 1988, 57, 801–808. [Google Scholar] [CrossRef]
- Slouka, Z.; Senapati, S.; Yan, Y.; Chang, H.-C. Charge inversion, water splitting, and vortex suppression due to DNA sorption on ion-selective membranes and their ion-current signatures. Langmuir 2012, 29, 8275–8283. [Google Scholar] [CrossRef]
- Lide, D.R. Handbook of Chemistry and Physics; CRC Press: New York, NY, USA, 1995. [Google Scholar]
- McMurry, J. Fundamentals of Organic Chemistry; Brooks/Cole; Cengage Learning: Belmont, NJ, USA, 2010. [Google Scholar]
- Mizutani, Y. Structure of ion exchange membranes. J. Membr. Sci. 1990, 49, 121–144. [Google Scholar] [CrossRef]
- Doi, S.; Yasukawa, M.; Kakihana, Y.; Higa, M. Alkali attack on anion exchange membranes with PVC backing and binder: Effect on performance and correlation between them. J. Membr. Sci. 2019, 573, 85–96. [Google Scholar] [CrossRef]
- Doi, S.; Kinoshita, M.; Yasukawa, M.; Higa, M. Alkali attack on anion exchange membranes with PVC backing and binder: II prediction of electrical and mechanical performances from simple optical analyses. Membranes 2018, 8, 133. [Google Scholar] [CrossRef] [PubMed]
- Güler, E.; van Baak, W.; Saakes, M.; Nijmeijer, K. Monovalent-ion-selective membranes for reverse electrodialysis. J. Membr. Sci. 2014, 455, 254–270. [Google Scholar] [CrossRef]
- Mareev, S.A.; Butylskii, D.Y.; Pismenskaya, N.D.; Larchet, C.; Dammak, L.; Nikonenko, V.V. Geometric heterogeneity of homogeneous ion-exchange Neosepta® membranes. J. Membr. Sci. 2018, 563, 768–776. [Google Scholar] [CrossRef]
- Ion Exchange Membranes for Water Purification. Brochure of Fujifilm Membrane Technology. Version number 1.0. 2018. Available online: https://www.fujifilmmembranes.com/water-membranes/ion-exchange-membranes (accessed on 1 July 2019).
- Rabolt, J.F.; Lee, K.H.; Givens, S.R. Method of Solution Preparation of Polyolefin Class Polymers for Electrospinning Processing Included. U.S. Patent 8,083,983 B2, 27 December 2011. [Google Scholar]
- Zhu, Y.; Ahmad, M.; Yang, L.; Misovich, M.; Yaroshchuk, A.; Bruening, M.L. Adsorption of polyelectrolyte multilayers imparts high monovalent/divalent cation selectivity to aliphatic polyamide cation-exchange membranes. J. Membr. Sci. 2017, 537, 177–185. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, J.; Wang, P.; Wang, Z.; Shi, F.; Liu, H. Investigations on the interfacial capacitance and the diffusion boundary layer thickness of ion exchange membrane using electrochemical impedance spectroscopy. J. Membr. Sci. 2016, 502, 37–47. [Google Scholar] [CrossRef]
- Antheunis, H.; Hessing, J.; Van Berchum, B. Curable Compositions and Membranes. U.S. Patent 8,968,965 B2, 3 March 2015. [Google Scholar]
- Berezina, N.P.; Timofeev, S.V.; Kononenko, N.A. Effect of conditioning techniques of perfluorinated sulphocationic membranes on their hydrophylic and electrotransport properties. J. Membr. Sci. 2002, 209, 509–518. [Google Scholar] [CrossRef]
- Volkov, A.I.; Zharskii, I.M. Comprehensive Chemical Handbook; Modern School: Moscow, Russia, 2005. [Google Scholar]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions; Butterworths: London, UK, 1959. [Google Scholar]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. Effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458–13469. [Google Scholar] [CrossRef]
- Rösler, H.-W.; Maletzki, F.; Staude, E. A numerical study of the hydrodynamic stable concentration boundary layers in a membrane system under microgravitational conditions. J. Membr. Sci. 1992, 72, 171–179. [Google Scholar] [CrossRef]
- Newman, J.S. Electrochemical Systems; Prentice Hall: Englewood Cliffs, NY, USA, 1973. [Google Scholar]
- Sheldeshov, N.V.; Ganych, V.V.; Zabolotsky, V.I. Transport numbers of salt ions and water dissociation products in cation and anion-exchange membranes. Sov. Electrochem. 1991, 23, 11–15. [Google Scholar]
- Laktionov, E.V.; Pismenskaya, N.D.; Nikonenko, V.V.; Zabolotsky, V.I. Method of electrodialysis stack testing with the feed solution concentration regulation. Desalination 2003, 152, 101–116. [Google Scholar] [CrossRef]
- Helfferich, F.G. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962; ASIN B0000CLGWI. [Google Scholar]
- Kwak, R.; Guan, G.; Peng, W.K.; Han, J. Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 2013, 308, 138–146. [Google Scholar] [CrossRef]
- Mareev, S.A.; Butylskii, D.Y.; Kovalenko, A.V.; Petukhova, A.V.; Pismenskaya, N.D.; Dammak, L.; Larchet, C.; Nikonenko, V.V. Accounting for the concentration dependence of electrolyte diffusion coefficient in the Sand and the Peers equations. Electrochim. Acta 2016, 195, 85–93. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]








| Electrolyte, pH | Diffusion Coefficients at Infinite Dilution, Di, 10−5 cm2s−1 | Transport Numbers at Infinite Dilution | Theoretical Limiting Current Density in 0.02 M Solution *, mA cm−2 | Diffusion Layer Thickness *, μm | |||
|---|---|---|---|---|---|---|---|
| Cation | Anion | Electrolyte | Cation | Anion | |||
| NaCl pH = 5.70 ± 0.05 | 1.334 [61,74] | 2.032 [61] | 1.61 [75] | 0.396 | 0.604 | 3.07 | 256 |
| NaH2PO4 pH = 4.60 ± 0.05 | 0.959 [61] | 1.11 [74] | 0.581 | 0.419 | 1.62 | 225 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rybalkina, O.; Tsygurina, K.; Melnikova, E.; Mareev, S.; Moroz, I.; Nikonenko, V.; Pismenskaya, N. Partial Fluxes of Phosphoric Acid Anions through Anion-Exchange Membranes in the Course of NaH2PO4 Solution Electrodialysis. Int. J. Mol. Sci. 2019, 20, 3593. https://doi.org/10.3390/ijms20143593
Rybalkina O, Tsygurina K, Melnikova E, Mareev S, Moroz I, Nikonenko V, Pismenskaya N. Partial Fluxes of Phosphoric Acid Anions through Anion-Exchange Membranes in the Course of NaH2PO4 Solution Electrodialysis. International Journal of Molecular Sciences. 2019; 20(14):3593. https://doi.org/10.3390/ijms20143593
Chicago/Turabian StyleRybalkina, Olesya, Kseniya Tsygurina, Ekaterina Melnikova, Semyon Mareev, Ilya Moroz, Victor Nikonenko, and Natalia Pismenskaya. 2019. "Partial Fluxes of Phosphoric Acid Anions through Anion-Exchange Membranes in the Course of NaH2PO4 Solution Electrodialysis" International Journal of Molecular Sciences 20, no. 14: 3593. https://doi.org/10.3390/ijms20143593
APA StyleRybalkina, O., Tsygurina, K., Melnikova, E., Mareev, S., Moroz, I., Nikonenko, V., & Pismenskaya, N. (2019). Partial Fluxes of Phosphoric Acid Anions through Anion-Exchange Membranes in the Course of NaH2PO4 Solution Electrodialysis. International Journal of Molecular Sciences, 20(14), 3593. https://doi.org/10.3390/ijms20143593