Various Approaches to Studying the Phase Transition in an Octamethylcyclotetrasiloxane Crystal: From X-ray Structural Analysis to Metadynamics
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Crystal Structure of the Low- and High-Temperature Phases of Octamethylcyclotetrasiloxane
2.2. Differential Scanning Calorimetry Studies
2.3. The Comparison of Experimental and Calculated ADPs
2.4. Phonon Spectra and Physical Properties
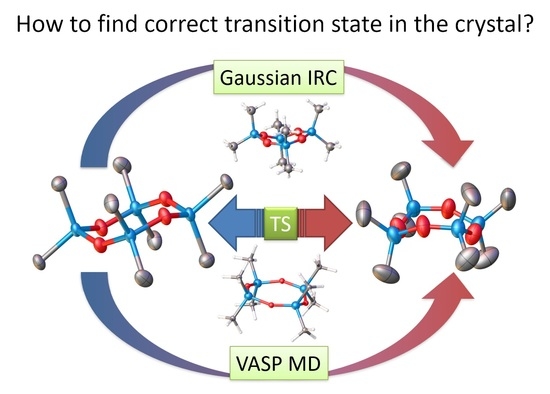
2.5. Phase Transition Simulation
3. Materials and Methods
3.1. X-ray Experimental Studies
3.2. Differential Scanning Calorimetry
3.3. Calculations
3.4. Mathematical Introduction and Theory
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shin, M.; Matsuda, K.; Ishii, O.; Terai, H.; Kaazempur-Mofrad, M.; Borenstein, J.; Detmar, M.; Vacanti, J.P. Endothelialized Networks with a Vascular Geometry in Microfabricated Poly(Dimethyl Siloxane). Biomed. Microdevices 2004, 6, 269–278. [Google Scholar] [CrossRef] [PubMed]
- Shams, E.; Yeganeh, H.; Naderi-Manesh, H.; Gharibi, R.; Mohammad Hassan, Z. Polyurethane/Siloxane Membranes Containing Graphene Oxide Nanoplatelets as Antimicrobial Wound Dressings: In Vitro and in Vivo Evaluations. J. Mater. Sci. Mater. Med. 2017, 28, 75. [Google Scholar] [CrossRef] [PubMed]
- Racles, C.; Zaltariov, M.-F.; Iacob, M.; Silion, M.; Avadanei, M.; Bargan, A. Siloxane-Based Metal-Organic Frameworks with Remarkable Catalytic Activity in Mild Environmental Photodegradation of Azo Dyes. Appl. Catal. B Environ. 2017, 205, 78–92. [Google Scholar] [CrossRef]
- Baskaran, T.; Kumaravel, R.; Christopher, J.; Radhakrishnan, S.; Sakthivel, A. Synthesis and Heterogenization of Siloxane Functionalized Cobalt Complex: Potential Catalyst for Oxidation of Alcohols. Catal. Lett. 2015, 145, 851–859. [Google Scholar] [CrossRef]
- Naka, K.; Irie, Y. Synthesis of Single Component Element-Block Materials Based on Siloxane-Based Cage Frameworks: Single Component Element-Block Materials. Polym. Int. 2017, 66, 187–194. [Google Scholar] [CrossRef]
- Saraswathy, M.; Stansbury, J.; Nair, D. Water Dispersible Siloxane Nanogels: A Novel Technique to Control Surface Characteristics and Drug Release Kinetics. J. Mater. Chem. B 2016, 4, 5299–5307. [Google Scholar] [CrossRef]
- Hoffman, J.D. Thermal and Dielectric Study of Octamethylcyclotetrasiloxane. J. Am. Chem. Soc. 1953, 75, 6313–6314. [Google Scholar] [CrossRef]
- Steinfink, H.; Post, B.; Fankuchen, I. The Crystal Structure of Octamethyl Cyclotetrasiloxane. Acta Crystallogr. 1955, 8, 420–424. [Google Scholar] [CrossRef]
- Shklover, V.E.; Kalinin, A.E.; Gusev, A.I.; Bokii, N.G.; Struchkov, Y.T.; Andrianov, K.A.; Petrova, I.M. Crystal Structures of Cyclic Siloxanes: II. 1,1,2,2-Tetramethyl-3,3,4,4-Tetraphenylcyclotetrasiloxane. J. Struct. Chem. 1974, 14, 639–645. [Google Scholar] [CrossRef]
- Brodalla, D.; Mootz, D.; Boese, R.; Osswald, W. Programmed Crystal Growth on a Diffractometer with Focused Heat Radiation. J. Appl. Crystallogr. 1985, 18, 316–319. [Google Scholar] [CrossRef]
- Boese, R. Special Issue on In Situ Crystallization. Z. für Krist. Cryst. Mater. 2014, 229, 595–601. [Google Scholar] [CrossRef]
- Volodin, A.D.; Korlyukov, A.A.; Smol’yakov, A.F. Organoelement Compounds Crystallized In Situ: Weak Intermolecular Interactions and Lattice Energies. Crystals 2019, 10, 15. [Google Scholar] [CrossRef]
- Lipscomb, W.N.; Streib, W.E. Growth, Orientation, and X-Ray Diffraction of Single Crystals near Liquid Helium Temperatures. Proc. Natl. Acad Sci. USA 1962, 48, 911–913. [Google Scholar]
- Smith, H.W.; Lipscomb, W.N. Single-Crystal X-Ray Diffraction Study of β-Diborane. J. Chem. Phys. 1965, 43, 1060–1064. [Google Scholar] [CrossRef]
- Antipin, M.Y. Low-Temperature X-Ray Diffraction Analysis: Possibilities in the Solution of Chemical Problems. Russ. Chem. Rev. 1990, 59, 607–626. [Google Scholar] [CrossRef]
- Boese, R.; Antipin, M.Y.; Nussbaumer, M.; Bläser, D. The Molecular and Crystal Structure of 4-Methoxybenzylidene-4′-n-Butylaniline (MBBA) at −163°C. Liq. Cryst. 1992, 12, 431–440. [Google Scholar] [CrossRef]
- Boese, R.; Nussbaumer, M. In Situ Crystallisation Techniques; Oxford University Press: Oxford, UK, 1994; Volume 7, p. 20. [Google Scholar]
- Bond, A.D.; Davies, J.E. In Situ Crystallization of the Linear Alkynes Cn H2n-2 (N = 7, 8, 9, 10). Z. Für Krist. Cryst. Mater. 2014, 229, 661–666. [Google Scholar] [CrossRef]
- Nath, N.K.; Naumov, P. In Situ Crystallization and Crystal Structure Determination of Chlorobenzene. Maced. J. Chem. Chem. Eng. 2015, 34, 63–66. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Peng, C.; Bernhard Schlegel, H. Combining Synchronous Transit and Quasi-Newton Methods to Find Transition States. Isr. J. Chem. 1993, 33, 449–454. [Google Scholar] [CrossRef]
- Peng, C.; Ayala, P.Y.; Schlegel, H.B.; Frisch, M.J. Using Redundant Internal Coordinates to Optimize Equilibrium Geometries and Transition States. J. Comput. Chem. 1996, 17, 49–56. [Google Scholar] [CrossRef]
- Laio, A.; Rodriguez-Fortea, A.; Gervasio, F.L.; Ceccarelli, M.; Parrinello, M. Assessing the Accuracy of Metadynamics. J. Phys. Chem. B 2005, 109, 6714–6721. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Frisch, M.J. Energy-Represented Direct Inversion in the Iterative Subspace within a Hybrid Geometry Optimization Method. J. Chem. Theory Comput. 2006, 2, 835–839. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. WIREs Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Tiwary, P.; Parrinello, M. From Metadynamics to Dynamics. Phys. Rev. Lett. 2013, 111, 230602. [Google Scholar] [CrossRef]
- Tycko, R.; Dabbagh, G.; Fleming, R.M.; Haddon, R.C.; Makhija, A.V.; Zahurak, S.M. Molecular Dynamics and the Phase Transition in Solid C60. Phys. Rev. Lett. 1991, 67, 1886–1889. [Google Scholar] [CrossRef]
- Schelling, P.K.; Phillpot, S.R.; Wolf, D. Mechanism of the Cubic-to-Tetragonal Phase Transition in Zirconia and Yttria-Stabilized Zirconia by Molecular-Dynamics Simulation. J. Am. Ceram. Soc. 2001, 84, 1609–1619. [Google Scholar] [CrossRef]
- Landau, L.D. On the Theory of Phase Transitions. I. Zh. Eksp. Teor. Fiz. 1937, 11, 19. [Google Scholar] [CrossRef]
- Sheldrick, G.M. CELL NOW Program for Unit Cell Determination; Göttingen University: Göttingen, Germany, 2003. [Google Scholar]
- Sheldrick, G.M. SHELXT–Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-Conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements. J. Phys. Condens. Matter 1994, 6, 8245–8257. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Nosé, S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision, A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Alfè, D. PHON: A Program to Calculate Phonons Using the Small Displacement Method. Comput. Phys. Commun. 2009, 180, 2622–2633. [Google Scholar] [CrossRef]











| Temperature, K | ||||||
|---|---|---|---|---|---|---|
| Si | O | C | Si | O | C | |
| 100 | 16.515 | 21.937 | 26.866 | 17.838 | 28.643 | 34.753 |
| 150 | 23.682 | 30.892 | 38.581 | 22.447 | 32.650 | 40.655 |
| 200 | 30.027 | 39.202 | 49.814 | 30.779 | 42.338 | 57.780 |
| 210 | 31.883 | 41.93 | 53.364 | 37.851 | 47.740 | 89.316 |
| 221 | 34.277 | 44.518 | 56.858 | 38.193 | 53.145 | 74.892 |
| 230 | 35.827 | 48.093 | 60.622 | 75.543 | 93.211 | 142.686 |
| 240 | 54.897 | 69.820 | 109.33 | 65.665 | 97.464 | 134.831 |
| 250 | 57.437 | 72.773 | 114.994 | 56.689 | 68.092 | 151.815 |
| 270 | 68.383 | 85.827 | 131.237 | 45.922 | 70.727 | 107.603 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volodin, A.D.; Smol’yakov, A.F.; Korlyukov, A.A. Various Approaches to Studying the Phase Transition in an Octamethylcyclotetrasiloxane Crystal: From X-ray Structural Analysis to Metadynamics. Int. J. Mol. Sci. 2022, 23, 9073. https://doi.org/10.3390/ijms23169073
Volodin AD, Smol’yakov AF, Korlyukov AA. Various Approaches to Studying the Phase Transition in an Octamethylcyclotetrasiloxane Crystal: From X-ray Structural Analysis to Metadynamics. International Journal of Molecular Sciences. 2022; 23(16):9073. https://doi.org/10.3390/ijms23169073
Chicago/Turabian StyleVolodin, Alexander D., Alexander F. Smol’yakov, and Alexander A. Korlyukov. 2022. "Various Approaches to Studying the Phase Transition in an Octamethylcyclotetrasiloxane Crystal: From X-ray Structural Analysis to Metadynamics" International Journal of Molecular Sciences 23, no. 16: 9073. https://doi.org/10.3390/ijms23169073
APA StyleVolodin, A. D., Smol’yakov, A. F., & Korlyukov, A. A. (2022). Various Approaches to Studying the Phase Transition in an Octamethylcyclotetrasiloxane Crystal: From X-ray Structural Analysis to Metadynamics. International Journal of Molecular Sciences, 23(16), 9073. https://doi.org/10.3390/ijms23169073