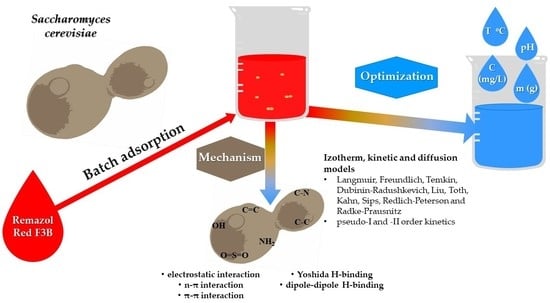
Linear and Nonlinear Regression Analysis for the Adsorption of Remazol Dye by Romanian Brewery Waste By-Product, Saccharomyces cerevisiae
Abstract
:1. Introduction
2. Results and Discussion
2.1. Optimization through Experiments
2.2. Characterization of Adsorbent
2.3. Interpretation of Adsorption Isotherm, Kinetic and Diffusion Models
- The pseudo-first-order model was not sufficiently accurate in the analysis of kinetic data for either linear or nonlinear fits;
- The R2 values of the pseudo-first-order model were low, and the calculated qe_calc differed greatly from the experimental results;
- Among the linearized pseudo-second-order kinetic models, pseudo II.1 showed more accurate results, where t/qt was plotted as a function of time t in the linearization (qe = 1/slope and k2 = slope2/intercept can be calculated from the equation linearized equation);
- The pseudo-second-order kinetic model, both the linearized (pseudo II.1) and the nonlinear models, applied with high accuracy for all the different concentrations;
- The pseudo-second-order kinetic model was a better representation of the kinetic behavior and, thus, more suitable for the determination of the rate constant and qe_calc;
- Excellent R2 values and good correlation between experimental (qe_exp) and calculated (qe_calc) values were obtained (pseudo II.1);
- The initial sorption rate h (g/mg/min; h = k2 × qe2) increased with the increase in initial dye concentration (h = 0.18, 0.72, 1.64, 3.02, 2.58, 3.98, 5.66), indicating the presence of a strong driving force for the mass transfer and an increased number of available active sites [56].
- Those describing the relationship between contaminant molecules or ions (RR dye) and active centers or binding sites on the surface of the adsorbent (brewer yeast), including pseudo-first-order and pseudo-second-order kinetic models;
- Diffusion models, which assume that in actual water treatment there is immediate diffusion between the contaminant and the active sites.
2.4. Possible Adsorption Mechanism
- Amide and amine bonds (R-NH-C-O-CH3-C-NH, −C-NH);
- (−C=O) and (−C-O) bonds, which are part of the chitin structure found in the sugar in the cell wall;
- The -C-N-C group found in the cell wall protein of yeast [24].
3. Materials and Methods
3.1. Adsorbent and Adsorbate
3.2. Adsorption Optimization
- The efficiency of liquid-phase adsorption, the sorption performance, is influenced by a number of physicochemical factors. To determine the optimum conditions, experiments were carried out with different initial parameters;
- The effects of initial RR dye concentration and contact time were studied at 5–1000 mg/L concentrations. Constant experimental parameters: 1.5/100 g/mL yeast, 20 °C, 700 rpm agitation speed, pH 6;
- During the study of the 0.5/1/1.5/2/2.5 g adsorbent dosages, yeast was added to a 5 mg/L dye solution at room temperature, which was agitated at 700 rpm and pH 6;
- The pH of the dye solution was adjusted between 2 and 11 with HCl or NaOH solutions in order to study the pH. Constant parameters: 1.5 g yeast, 100 mL of 20 mg/L RR dye, stable room temperature and stirring at 700 rpm;
- With the help of a IKA C-MAG HS7 magnetic shaker, the effect of temperature (20, 30, 40 °C) on adsorption was investigated. Samples contained 100 mL 20 mg/L RR dye solution stirred constantly at 700 rpm with 1.5 g yeast.
3.3. Analytical Studies
3.4. Isotherm, Kinetic and Diffusion Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Salehi, M. Global Water Shortage and Potable Water Safety; Today’s Concern and Tomorrow’s Crisis. Environ. Int. 2022, 158, 106936. [Google Scholar] [CrossRef] [PubMed]
- Lund Schlamovitz, J.; Becker, P. Differentiated Vulnerabilities and Capacities for Adaptation to Water Shortage in Gaborone, Botswana. Int. J. Water Resour. Dev. 2021, 37, 278–299. [Google Scholar] [CrossRef]
- Mishra, B.K.; Kumar, P.; Saraswat, C.; Chakraborty, S.; Gautam, A. Water Security in a Changing Environment: Concept, Challenges and Solutions. Water 2021, 13, 490. [Google Scholar] [CrossRef]
- Manoiu, V.-M.; Kubiak-Wójcicka, K.; Craciun, A.-I.; Akman, Ç.; Akman, E. Water Quality and Water Pollution in Time of COVID-19: Positive and Negative Repercussions. Water 2022, 14, 1124. [Google Scholar] [CrossRef]
- Varjani, S.; Rakholiya, P.; Shindhal, T.; Shah, A.V.; Ngo, H.H. Trends in Dye Industry Effluent Treatment and Recovery of Value Added Products. J. Water Process Eng. 2021, 39, 101734. [Google Scholar] [CrossRef]
- Common Objective The Issues: Water. Available online: http://www.commonobjective.co/article/the-issues-water (accessed on 11 September 2022).
- Katheresan, V.; Kansedo, J.; Lau, S.Y. Efficiency of Various Recent Wastewater Dye Removal Methods: A Review. J. Environ. Chem. Eng. 2018, 6, 4676–4697. [Google Scholar] [CrossRef]
- Gajera, R.; Patel, R.V.; Yadav, A.; Labhasetwar, P.K. Adsorption of Cationic and Anionic Dyes on Photocatalytic Flyash/TiO2 Modified Chitosan Biopolymer Composite. J. Water Process Eng. 2022, 49, 102993. [Google Scholar] [CrossRef]
- Rápó, E.; Tonk, S. Factors Affecting Synthetic Dye Adsorption; Desorption Studies: A Review of Results from the Last Five Years (2017–2021). Molecules 2021, 26, 5419. [Google Scholar] [CrossRef]
- Hussain, D.; Khan, S.A.; Khan, T.A.; Alharthi, S.S. Efficient Liquid Phase Confiscation of Nile Blue Using a Novel Hybrid Nanocomposite Synthesized from Guar Gum-Polyacrylamide and Erbium Oxide. Sci. Rep. 2022, 12, 14656. [Google Scholar] [CrossRef]
- Saxena, G.; Kishor, R.; Zainith, S.; Bharagava, R.N. Chapter 17—Environmental Contamination, Toxicity Profile and Bioremediation Technologies for Treatment and Detoxification of Textile Effluent. In Bioremediation for Environmental Sustainability; Saxena, G., Kumar, V., Shah, M.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 415–434. ISBN 978-0-12-820524-2. [Google Scholar]
- Kheradmand, A.; Negarestani, M.; Kazemi, S.; Shayesteh, H.; Javanshir, S.; Ghiasinejad, H. Adsorption Behavior of Rhamnolipid Modified Magnetic Co/Al Layered Double Hydroxide for the Removal of Cationic and Anionic Dyes. Sci. Rep. 2022, 12, 14623. [Google Scholar] [CrossRef]
- Piron, E.; Poelmans, E. Beer, the Preferred Alcoholic Drink of All? Changes in the Global and National Beer Consumption Since 1960 and Convergence and Trends Since the 1990s. In Brewing, Beer and Pubs: A Global Perspective; Cabras, I., Higgins, D., Preece, D., Eds.; Palgrave Macmillan: London, UK, 2016; pp. 205–227. ISBN 978-1-137-46618-1. [Google Scholar]
- Durán-Sánchez, A.; de la Cruz del Río-Rama, M.; Álvarez-García, J.; Oliveira, C. Analysis of Worldwide Research on Craft Beer. SAGE Open 2022, 12, 21582440221108150. [Google Scholar] [CrossRef]
- Jantyik, L.; Balogh, J.M.; Török, Á. What Are the Reasons Behind the Economic Performance of the Hungarian Beer Industry? The Case of the Hungarian Microbreweries. Sustainability 2021, 13, 2829. [Google Scholar] [CrossRef]
- Conway, J. Beer Industry—Statistics & Facts. Available online: https://www.statista.com/topics/1654/beer-production-and-distribution/ (accessed on 28 December 2020).
- Smarter Business: The Top 5 Industries That Consume the Most Water. Available online: https://smarterbusiness.co.uk/blogs/the-top-5-industries-that-consume-the-most-water/ (accessed on 28 December 2020).
- Jaeger, A.; Arendt, E.K.; Zannini, E.; Sahin, A.W. Brewer’s Spent Yeast (BSY), an Underutilized Brewing By-Product. Fermentation 2020, 6, 123. [Google Scholar] [CrossRef]
- Al-Najar, J.A.; Lutfee, T.; Alwan, N.F. The Action of Yeast as an Adsorbent in Wastewater Treatment: A Brief Review. IOP Conf. Ser. Earth Environ. Sci. 2021, 779, 012054. [Google Scholar] [CrossRef]
- Hamzah, S.; Swan, N.; Razali, N.; Mohamad, N.; Rasit, N.; Ali, A.; Sulaiman, M.; Jusoh, A.; Hairom, N.H.H.; Nora’aini, A.; et al. Integration of Water Treatment Sludge and Agriculture Waste as Low-Cost Adsorbent for Remazol Red Dye Removal. Desalination Water Treat. 2021, 226, 408–418. [Google Scholar] [CrossRef]
- Soltani, A.; Faramarzi, M.; Mousavi Parsa, S.A. A Review on Adsorbent Parameters for Removal of Dye Products from Industrial Wastewater. Water Qual. Res. J. 2021, 56, 181–193. [Google Scholar] [CrossRef]
- Rápó, E.; Aradi, L.E.; Szabó, Á.; Posta, K.; Szép, R.; Tonk, S. Adsorption of Remazol Brilliant Violet-5R Textile Dye from Aqueous Solutions by Using Eggshell Waste Biosorbent. Sci. Rep. 2020, 10, 8385. [Google Scholar] [CrossRef]
- Subramani, S.E.; Thinakaran, N. Isotherm, Kinetic and Thermodynamic Studies on the Adsorption Behaviour of Textile Dyes onto Chitosan. Process Saf. Environ. Prot. 2017, 106, 1–10. [Google Scholar] [CrossRef]
- Dilarri, G.; de Almeida, É.J.R.; Pecora, H.B.; Corso, C.R. Removal of Dye Toxicity from an Aqueous Solution Using an Industrial Strain of Saccharomyces Cerevisiae (Meyen). Water Air Soil Pollut. 2016, 227, 269. [Google Scholar] [CrossRef] [Green Version]
- Bello, O.S.; Ahmad, M.A. Removal of Remazol Brilliant Violet-5R Dye Using Periwinkle Shells. Chem. Ecol. 2011, 27, 481–492. [Google Scholar] [CrossRef]
- Bello, O.S.; Ahmad, M.A. Response Surface Modeling and Optimization of Remazol Brilliant Blue Reactive Dye Removal Using Periwinkle Shell-Based Activated Carbon. Sep. Sci. Technol. 2011, 46, 2367–2379. [Google Scholar] [CrossRef]
- Patel, H. Equilibrium, Kinetic and Thermodynamic Stuies on Adsorption of Reactive Dyes onto Activated Guava Leaf Powder. Fresenius Environ. Bull. 2011, 20, 561–568. [Google Scholar]
- Ejikeme, P.C.N.; Ejikeme, E.M.; Okonkwo, G.N. Equilibrium, Kinetic and Thermodynamic Stuies on Basic Dye Adsorption Using Composite Activated Carbon. Int. J. Tech. Res. Appl. 2014, 2, 96–103. [Google Scholar]
- Baskar, A.V.; Bolan, N.; Hoang, S.A.; Sooriyakumar, P.; Kumar, M.; Singh, L.; Jasemizad, T.; Padhye, L.P.; Singh, G.; Vinu, A.; et al. Recovery, Regeneration and Sustainable Management of Spent Adsorbents from Wastewater Treatment Streams: A Review. Sci. Total Environ. 2022, 822, 153555. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodi, N.M.; Oveisi, M.; Taghizadeh, A.; Taghizadeh, M. Synthesis of Pearl Necklace-like ZIF-8@chitosan/PVA Nanofiber with Synergistic Effect for Recycling Aqueous Dye Removal. Carbohydr. Polym. 2020, 227, 115364. [Google Scholar] [CrossRef] [PubMed]
- Patel, H. Review on Solvent Desorption Study from Exhausted Adsorbent. J. Saudi Chem. Soc. 2021, 25, 101302. [Google Scholar] [CrossRef]
- Nouri, H.; Azin, E.; Kamyabi, A.; Moghimi, H. Biosorption Performance and Cell Surface Properties of a Fungal-Based Sorbent in Azo Dye Removal Coupled with Textile Wastewater. Int. J. Environ. Sci. Technol. 2021, 18, 2545–2558. [Google Scholar] [CrossRef]
- Ami, D.; Posteri, R.; Mereghetti, P.; Porro, D.; Doglia, S.M.; Branduardi, P. Fourier Transform Infrared Spectroscopy as a Method to Study Lipid Accumulation in Oleaginous Yeasts. Biotechnol. Biofuels 2014, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Stafussa, A.P.; Maciel, G.M.; da Silva Anthero, A.G.; da Silva, M.V.; Zielinski, A.A.F.; Haminiuk, C.W.I. Biosorption of Anthocyanins from Grape Pomace Extracts by Waste Yeast: Kinetic and Isotherm Studies. J. Food Eng. 2016, 169, 53–60. [Google Scholar] [CrossRef]
- Danouche, M.; el Arroussi, H.; el Ghachtouli, N. Bioremoval Mechanisms of Azo Dye Acid Red 14 Using Wickerhamomyces Anomalus Yeast Strain as a Natural Biosorbent. Res. Sq. 2021. Preprint. [Google Scholar] [CrossRef]
- Lesage, G.; Bussey, H. Cell Wall Assembly in Saccharomyces Cerevisiae. Microbiol. Mol. Biol. Rev. 2006, 70, 317–343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berterame, N.M.; Porro, D.; Ami, D.; Branduardi, P. Protein Aggregation and Membrane Lipid Modifications under Lactic Acid Stress in Wild Type and OPI1 Deleted Saccharomyces Cerevisiae Strains. Microbial. Cell Factories 2016, 15, 39. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, W.; Xu, M.; Zheng, F.; Zhao, M. Study of the Mechanisms of Cu2+ Biosorption by Ethanol/Caustic-Pretreated Baker’s Yeast Biomass. J. Hazard. Mater. 2010, 178, 1085–1093. [Google Scholar] [CrossRef] [PubMed]
- Bulik, D.A.; Olczak, M.; Lucero, H.A.; Osmond, B.C.; Robbins, P.W.; Specht, C.A. Chitin Synthesis in Saccharomyces Cerevisiae in Response to Supplementation of Growth Medium with Glucosamine and Cell Wall Stress. Eukaryot Cell 2003, 2, 886–900. [Google Scholar] [CrossRef] [Green Version]
- Kalam, S.; Abu-Khamsin, S.A.; Kamal, M.S.; Patil, S. Surfactant Adsorption Isotherms: A Review. ACS Omega 2021, 6, 32342–32348. [Google Scholar] [CrossRef]
- Suwannahong, K.; Wongcharee, S.; Kreetachart, T.; Sirilamduan, C.; Rioyo, J.; Wongphat, A. Evaluation of the Microsoft Excel Solver Spreadsheet-Based Program for Nonlinear Expressions of Adsorption Isotherm Models onto Magnetic Nanosorbent. Appl. Sci. 2021, 11, 7432. [Google Scholar] [CrossRef]
- Hossain, M.D.; Ngo, H.; Guo, W. Introductory of Microsoft Excel SOLVER Function-Spreadsheet Method for Isotherm and Kinetics Modelling of Metals Biosorption in Water and Wastewater. J. Water Sustain. 2013, 3, 223–237. [Google Scholar]
- Rajahmundry, G.K.; Garlapati, C.; Kumar, P.S.; Alwi, R.S.; Vo, D.-V.N. Statistical Analysis of Adsorption Isotherm Models and Its Appropriate Selection. Chemosphere 2021, 276, 130176. [Google Scholar] [CrossRef]
- Mozaffari Majd, M.; Kordzadeh-Kermani, V.; Ghalandari, V.; Askari, A.; Sillanpää, M. Adsorption Isotherm Models: A Comprehensive and Systematic Review (2010−2020). Sci. Total Environ. 2022, 812, 151334. [Google Scholar] [CrossRef]
- Amrhar, O.; El Gana, L.; Mobarak, M. Calculation of Adsorption Isotherms by Statistical Physics Models: A Review. Environ. Chem. Lett. 2021, 19, 4519–4547. [Google Scholar] [CrossRef]
- Tonk, S.; Aradi, L.E.; Kovács, G.; Turza, A.; Rápó, E. Effectiveness and Characterization of Novel Mineral Clay in Cd2+ Adsorption Process: Linear and Non-Linear Isotherm Regression Analysis. Water 2022, 14, 279. [Google Scholar] [CrossRef]
- Çelebi, H.; Gök, G.; Gök, O. Adsorption Capability of Brewed Tea Waste in Waters Containing Toxic Lead(II), Cadmium (II), Nickel (II), and Zinc(II) Heavy Metal Ions. Sci. Rep. 2020, 10, 17570. [Google Scholar] [CrossRef] [PubMed]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and Interpretation of Adsorption Isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Porkodi, K.; Rocha, F. Comparison of Various Error Functions in Predicting the Optimum Isotherm by Linear and Non-Linear Regression Analysis for the Sorption of Basic Red 9 by Activated Carbon. J. Hazard. Mater. 2008, 150, 158–165. [Google Scholar] [CrossRef] [PubMed]
- Amrhar, O.; Nassali, H.; Elyoubi, M. Application of Nonlinear Regression Analysis to Select the Optimum Absorption Isotherm for Methylene Blue Adsorption onto Natural Illitic Clay. Bull. Soc. R. Sci. Liege 2015, 84, 116–130. [Google Scholar]
- Kumar, K.V.; Porkodi, K. Relation between Some Two- and Three-Parameter Isotherm Models for the Sorption of Methylene Blue onto Lemon Peel. J. Hazard. Mater. 2006, 138, 633–635. [Google Scholar] [CrossRef]
- Saleh, T.A. Chapter 4—Isotherm Models of Adsorption Processes on Adsorbents and Nanoadsorbents. In Interface Science and Technology; Saleh, T.A., Ed.; Surface Science of Adsorbents and Nanoadsorbents; Elsevier: Amsterdam, The Netherlands, 2022; Volume 34, pp. 99–126. [Google Scholar]
- Tran, H.N.; Lima, E.C.; Juang, R.-S.; Bollinger, J.-C.; Chao, H.-P. Thermodynamic Parameters of Liquid–Phase Adsorption Process Calculated from Different Equilibrium Constants Related to Adsorption Isotherms: A Comparison Study. J. Environ. Chem. Eng. 2021, 9, 106674. [Google Scholar] [CrossRef]
- Hamdaoui, O.; Naffrechoux, E. Modeling of Adsorption Isotherms of Phenol and Chlorophenols onto Granular Activated Carbon. Part I. Two-Parameter Models and Equations Allowing Determination of Thermodynamic Parameters. J. Hazard. Mater. 2007, 147, 381–394. [Google Scholar] [CrossRef]
- Lima, É.C.; Adebayo, M.A.; Machado, F.M. Kinetic and Equilibrium Models of Adsorption. In Carbon Nanomaterials as Adsorbents for Environmental and Biological Applications; Bergmann, C.P., Machado, F.M., Eds.; Carbon Nanostructures; Springer International Publishing: Cham, Switzerland, 2015; pp. 33–69. ISBN 978-3-319-18875-1. [Google Scholar]
- Uddin, M.K.; Nasar, A. Walnut Shell Powder as a Low-Cost Adsorbent for Methylene Blue Dye: Isotherm, Kinetics, Thermodynamic, Desorption and Response Surface Methodology Examinations. Sci. Rep. 2020, 10, 7983. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption Kinetic Models: Physical Meanings, Applications, and Solving Methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- Pholosi, A.; Naidoo, E.B.; Ofomaja, A.E. Intraparticle Diffusion of Cr(VI) through Biomass and Magnetite Coated Biomass: A Comparative Kinetic and Diffusion Study. S. Afr. J. Chem. Eng. 2020, 32, 39–55. [Google Scholar] [CrossRef]
- Wu, F.-C.; Tseng, R.-L.; Juang, R.-S. Initial Behavior of Intraparticle Diffusion Model Used in the Description of Adsorption Kinetics. Chem. Eng. J. 2009, 153, 1–8. [Google Scholar] [CrossRef]
- Dutta, S.; Gupta, B.; Kumar Srivastava, S.; Kumar Gupta, A. Recent Advances on the Removal of Dyes from Wastewater Using Various Adsorbents: A Critical Review. Mater. Adv. 2021, 2, 4497–4531. [Google Scholar] [CrossRef]
- Danouche, M.; Arroussi, H.E.; Bahafid, W.; Ghachtouli, N.E. An Overview of the Biosorption Mechanism for the Bioremediation of Synthetic Dyes Using Yeast Cells. Environ. Technol. Rev. 2021, 10, 58–76. [Google Scholar] [CrossRef]
- De Castro, K.C.; Cossolin, A.S.; dos Reis, H.C.O.; de Morais, E.B.; de Castro, K.C.; Cossolin, A.S.; dos Reis, H.C.O.; de Morais, E.B. Biosorption of Anionic Textile Dyes from Aqueous Solution by Yeast Slurry from Brewery. Braz. Arch. Biol. Technol. 2017, 60, e17160101. [Google Scholar] [CrossRef]
- Sahoo, T.R.; Prelot, B. Adsorption Processes for the Removal of Contaminants from Wastewater. In Nanomaterials for the Detection and Removal of Wastewater Pollutants; Elsevier: Amsterdam, The Netherlands, 2020; pp. 161–222. ISBN 978-0-12-818489-9. [Google Scholar]








| Langmuir I | Langmuir II | Langmuir III | Langmuir IV | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| KL | qmax | R2 | KL | qmax | R2 | KL | qmax | R2 | KL | qmax | R2 |
| (L/mg) | (mg/g) | (L/mg) | (mg/g) | (L/mg) | (mg/g) | (L/mg) | (mg/g) | ||||
| 0.01 | 24.45 | 0.923 | 0.02 | 3.66 | 0.892 | 0.02 | 15.02 | 0.571 | 0.01 | 20.93 | 0.508 |
| Freundlich | Dubinin–Radushkevich | Temkin | |||||||||
| n | Kf | R2 | β | E | R2 | AT | B | R2 | |||
| (mg(1−1/n)L1/n/g) | (mol2 kJ2) | (kJ/mol) | (L/g) | (J/mol) | |||||||
| 1.45 | 3.02 | 0.921 | 4 × 10−6 | 0.35 | 0.712 | 2.35 | 4 × 10−5 | 0.898 | |||
| Isotherm Model | Factors for the Model | Statistical Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | ERRSQ/SSE | Chi-Square | ARE | RMSE | HYBRID | MPSD | ||||
| Langmuir | qm | KL | 0.9773 | 14.68 | 3.60 | 16.51 | 1.02 | 18.87 | 186.77 | |
| 0.005 | 27.165 | |||||||||
| Freundlich | KF | nF | 0.9937 | 4.09 | 6.00 | −42.22 | 0.54 | −48.25 | 477.66 | |
| 0.728 | 1.904 | |||||||||
| Temkin | bt | KT | 0.8980 | 66.03 | 48.06 | 98.96 | 2.17 | 113.09 | 1119.58 | |
| 3.339 | 0.235 | |||||||||
| Dubinin–Radushkevich | qD-R | KD-R | 0.8465 | 99.40 | 20.39 | 51.70 | 2.66 | 59.08 | 584.89 | |
| 17.351 | 0.001 | |||||||||
| Toth | qm | KToth | nToth | 0.9251 | 1246.32 | 92.26 | 74.04 | 9.44 | 84.62 | 837.72 |
| 1.233 | 0.267 | 0.551 | ||||||||
| Kahn | qm | KK | aK | 0.9960 | 2.56 | 1.86 | −19.61 | 0.43 | −22.42 | 221.92 |
| 2.241 | 0.162 | 0.514 | ||||||||
| Liu | qm | KLiu | nLiu | 0.9948 | 3.38 | 3.74 | −30.67 | 0.49 | −35.05 | 347.01 |
| 86.992 | 0 | 1.660 | ||||||||
| Sips | qm | KS | nS | 0.9948 | 3.38 | 3.76 | −30.76 | 0.49 | −35.15 | 348.00 |
| 87.317 | 0.007 | 0.602 | ||||||||
| Redlich–Peterson | KRP | a | n | 0.9957 | 2.80 | 2.35 | −22.72 | 0.45 | −25.96 | 257.02 |
| 0.599 | 0.484 | 0.551 | ||||||||
| Radke–Prausnitz | qm | K | n | 0.9937 | 4.09 | 5.99 | −42.18 | 0.54 | −48.21 | 477.25 |
| 0.728 | 1.06 × 1046 | 0.475 | ||||||||
| Kinetic Model | Pseudo I | Pseudo I | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Type of Fitting | LINEAR: ln(1-qt/qe) vs. t | NONLINEAR: qe × (1-exp(−k1 × t)) | |||||||
| Parameters | k1 | R2 | qe_calc. | qe_calc. | k1 | Statistics | |||
| Value | Standard Error | Value | Standard Error | Red. χ2 | Adj. R2 | ||||
| 5 mg/L | 0.008 | 0.902 | 0.06 | 0.17 | 0.01 | 0.62 | 0.17 | 0.001 | 0.286 |
| 10 mg/L | 0.023 | 0.916 | 0.43 | 0.43 | 0.01 | 0.89 | 0.16 | 0.001 | 0.535 |
| 20 mg/L | 0.017 | 0.953 | 0.39 | 0.95 | 0.02 | 0.92 | 0.18 | 0.007 | 0.433 |
| 30 mg/L | 0.015 | 0.947 | 0.60 | 1.37 | 0.03 | 1.10 | 0.17 | 0.009 | 0.509 |
| 40 mg/L | 0.011 | 0.973 | 0.36 | 1.98 | 0.05 | 0.69 | 0.12 | 0.036 | 0.461 |
| 50 mg/L | 0.012 | 0.979 | 0.40 | 2.42 | 0.06 | 0.88 | 0.16 | 0.046 | 0.423 |
| 60 mg/L | 0.020 | 0.978 | 0.39 | 2.97 | 0.07 | 1.06 | 0.22 | 0.072 | 0.308 |
| Kinetic model | Pseudo II.1 | Pseudo II.2 | Pseudo II.3 | ||||||
| Type of fitting | LINEAR: t/qt vs. t | LINEAR: 1/t vs. 1/qt | LINEAR: 1/qt vs. 1/t | ||||||
| Parameter | k2 | R2 | qe_calc. | k2 | R2 | qe_calc. | k2 | R2 | qe_calc. |
| 5 mg/L | 0.84 | 0.9933 | 0.20 | 10.32 | 0.609 | 0.58 | 5.52 | 0.609 | 1.02 |
| 10 mg/L | 1.44 | 0.9997 | 0.47 | 4.48 | 0.895 | 0.51 | 3.92 | 0.895 | 0.57 |
| 20 mg/L | 0.42 | 0.9995 | 1.04 | 2.18 | 0.817 | 0.47 | 1.73 | 0.817 | 0.59 |
| 30 mg/L | 0.46 | 0.9999 | 1.46 | 1.75 | 0.884 | 0.41 | 1.53 | 0.884 | 0.46 |
| 40 mg/L | 0.14 | 0.9997 | 2.15 | 0.88 | 0.760 | 0.57 | 0.64 | 0.760 | 0.77 |
| 50 mg/L | 0.13 | 0.9996 | 2.64 | 0.83 | 0.797 | 0.49 | 0.64 | 0.797 | 0.62 |
| 60 mg/L | 0.15 | 0.9998 | 3.21 | 0.81 | 0.725 | 0.41 | 0.56 | 0.725 | 0.58 |
| Kinetic model | Pseudo II.4 | Pseudo II.5 | Pseudo II.6 | ||||||
| Type of fitting | LINEAR: 1/qt vs. 1/t | LINEAR: 1/qt vs. 1/t | LINEAR: 1/qt vs. 1/t | ||||||
| Parameter | k2 | R2 | qe_calc. | k2 | R2 | qe_calc. | k2 | R2 | qe_calc. |
| 5 mg/L | 0.20 | 0.928 | 0.07 | 2.56 | 0.512 | 0.26 | 0.18 | 0.512 | 0.14 |
| 10 mg/L | 1.90 | 0.635 | 0.07 | 0.67 | 0.865 | 0.81 | 0.45 | 0.865 | 0.72 |
| 20 mg/L | 0.41 | 0.871 | 0.43 | 0.27 | 0.771 | 1.92 | 1.00 | 0.771 | 1.51 |
| 30 mg/L | 0.26 | 0.906 | 0.48 | 0.13 | 0.850 | 3.30 | 1.42 | 0.850 | 2.83 |
| 40 mg/L | 0.15 | 0.887 | 0.54 | 0.19 | 0.716 | 3.28 | 2.06 | 0.716 | 2.40 |
| 50 mg/L | 0.11 | 0.889 | 1.95 | 0.11 | 0.747 | 4.70 | 2.53 | 0.747 | 3.58 |
| 60 mg/L | 0.90 | 0.551 | 0.04 | 0.06 | 0.693 | 6.94 | 3.11 | 0.693 | 4.92 |
| Kinetic model | Pseudo II | Experimental Result | |||||||
| Type of fitting | NONLINEAR: qe2×k2×t/(1 + k2×qe×t) | ||||||||
| Parameter | qe_calc. | k2 | Statistics | ||||||
| Value | Standard Error | Value | Standard Error | Red. χ2 | Adj. R2 | qe_exp. | |||
| 5 mg/L | 0.18 | 0.01 | 5.83 | 1.85 | 3.70 × 10−4 | 0.583 | 0.20 | ||
| 10 mg/L | 0.45 | 0.01 | 3.59 | 0.49 | 2.87 × 10−4 | 0.894 | 0.47 | ||
| 20 mg/L | 0.99 | 0.02 | 1.68 | 0.30 | 0.002 | 0.806 | 1.04 | ||
| 30 mg/L | 1.41 | 0.02 | 1.51 | 0.20 | 0.002 | 0.864 | 1.46 | ||
| 40 mg/L | 2.04 | 0.03 | 0.62 | 0.11 | 0.014 | 0.788 | 2.15 | ||
| 50 mg/L | 2.50 | 0.04 | 0.64 | 0.11 | 0.017 | 0.782 | 2.63 | ||
| 60 mg/L | 3.07 | 0.05 | 0.60 | 0.11 | 0.026 | 0.748 | 3.20 | ||
| Intra-Particle Diffusion | Liquid-Film Diffusion | ||||||
|---|---|---|---|---|---|---|---|
| C (mg/L) | D (cm2/s) | kip (mg/g∙min1/2) | Intercept | R2ip | kfd (1/min) | Intercept | R2fd |
| 5 | 8.31 × 10−9 | 0.006 | 0.122 | 0.956 | 0.008 | 1.05 | 0.902 |
| 10 | 3.34 × 10−8 | 0.011 | 0.355 | 0.752 | 0.023 | 1.53 | 0.916 |
| 20 | 2.19 × 10−8 | 0.021 | 0.787 | 0.846 | 0.017 | 1.48 | 0.953 |
| 30 | 3.34 × 10−8 | 0.021 | 1.191 | 0.767 | 0.015 | 1.82 | 0.947 |
| 40 | 1.53 × 10−8 | 0.037 | 1.583 | 0.837 | 0.011 | 1.44 | 0.973 |
| 50 | 1.68 × 10−8 | 0.043 | 2.001 | 0.865 | 0.012 | 1.49 | 0.979 |
| 60 | 2.43 × 10−8 | 0.055 | 2.501 | 0.841 | 0.020 | 1.48 | 0.971 |
| C | qref | C/qref | Ri |
|---|---|---|---|
| 2.00 | 0.20 | 10.0 | −9.0 |
| 3.00 | 0.47 | 6.4 | −5.4 |
| 4.43 | 1.04 | 4.3 | −3.3 |
| 8.03 | 1.46 | 5.5 | −4.5 |
| 7.77 | 2.15 | 3.6 | −2.6 |
| 10.5 | 2.63 | 4.0 | −3.0 |
| 11.97 | 3.20 | 3.7 | −2.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tonk, S.; Rápó, E. Linear and Nonlinear Regression Analysis for the Adsorption of Remazol Dye by Romanian Brewery Waste By-Product, Saccharomyces cerevisiae. Int. J. Mol. Sci. 2022, 23, 11827. https://doi.org/10.3390/ijms231911827
Tonk S, Rápó E. Linear and Nonlinear Regression Analysis for the Adsorption of Remazol Dye by Romanian Brewery Waste By-Product, Saccharomyces cerevisiae. International Journal of Molecular Sciences. 2022; 23(19):11827. https://doi.org/10.3390/ijms231911827
Chicago/Turabian StyleTonk, Szende, and Eszter Rápó. 2022. "Linear and Nonlinear Regression Analysis for the Adsorption of Remazol Dye by Romanian Brewery Waste By-Product, Saccharomyces cerevisiae" International Journal of Molecular Sciences 23, no. 19: 11827. https://doi.org/10.3390/ijms231911827
APA StyleTonk, S., & Rápó, E. (2022). Linear and Nonlinear Regression Analysis for the Adsorption of Remazol Dye by Romanian Brewery Waste By-Product, Saccharomyces cerevisiae. International Journal of Molecular Sciences, 23(19), 11827. https://doi.org/10.3390/ijms231911827