Hiding the Source Based on Limited Flooding for Sensor Networks
Abstract
:1. Introduction
2. Related Work
3. Problem Definition
3.1. Network Model
- Sensors are deployed evenly over the whole network. Any two sensors can communicate with each other hop-by-hop.
- Only one sink exists as the controller of the network. The sink collects or retrieves data from sensors from time to time.
3.2. Attack Model
3.3. Security Assumption
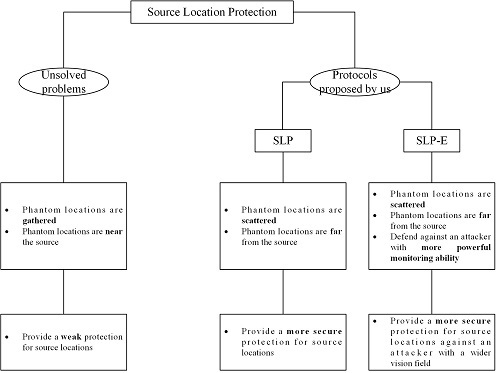
4. Protocol for Source Location Protection Based on Limited Flooding
| (Kpub, Kpri) | The public/private key pair for packet encryption and decryption |
| EKpub(m) | Encrypt packet m by public key Kpub |
| bs | Base station |
| Hopu,v | The shortest distance from sensor u to sensor v measured by hops |
| pi | Phantom location |
| u.neighbor | The set of sensor u’ neighbors |
| u.set_parent | {v|v∈u.neighbor∩Hopv,b < Hopu,b} |
| r | The visual radius for the attacker |
| h | The random directed hops |
| The hops from sensor u to sensor v along the inferior arc | |
| H | The shortest distance from source to the base station measured by hops |
| R | Transmission range of a sensor |
| A path from sensor u to v |
4.1. Network Initialization
4.2. h-Hops Limited Flooding Initialized from the Source
4.3. h-Directed Routing
4.4. The Shortest Path Routing
5. Protocol for Source Location Protection Enhancement Based on Limited Flooding

6. Performance Analysis
6.1. Communication Cost

- When γ=π, SLP-E achieves the maximum communication cost of . In this case, the packet first arrives at the phantom location p5 and then at the base station through the line passing through p5 and b.
- When α = 0, SLP-E achieves the minimum communication cost of H. In this case, the packet first arrives at the phantom location p6 and then at the base station through the line passing through p6 and b.
- The average communication cost of SLP-E is:
- (a)
- f = 0 if p3 is on ;
- (b)
- f = + HopF,b-HopE,b if p3 is on .
| r/H | 1/2 | 1/5 | 1/10 | 1/15 | 1/20 |
| favg | 28 | 8 | 3 | 2 | 1 |
6.2. Computation Cost
6.3. Security Performance

| h = 2 | h = 20 | h = 30 | h = 40 | h = 50 | h = 60 | |
|---|---|---|---|---|---|---|
| SLP | 33.33% | 79.78% | 83.52% | 85.73% | 87.15% | 88.36% |
6.4. Communication Cost vs. Security
7. Simulation Results
7.1. Communication Cost


7.2. Security Performance


8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, H.; Lou, W. On protecting end-to-end location privacy against local eavesdropper in Wireless Sensor Networks. J. Pervasive Mob. Comput. 2015, 16, 36–50. [Google Scholar] [CrossRef]
- Raj, M.; Li, N.; Liu, D.; Wright, M.; Das, S.K. Using data mules to preserve source location privacy in Wireless Sensor Networks. J. Pervasive Mob. Comput. 2014, 11, 244–260. [Google Scholar] [CrossRef]
- Ozturk, C.; Zhang, Y.; Trappe, W. Source-location privacy in energy constrained sensor networks routing. In Proceedings of the 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks, Washington, DC, USA, 25–29 October 2004; pp. 88–93.
- Kamat, P.; Zhang, Y.; Trappe, W.; Ozturk, C. Enhancing source-location privacy in sensor network routing. In Proceedings of the 25th IEEE International Conference on Distributed Computing Systems, Columbus, OH, USA, 10 June 2005; pp. 599–608.
- Li, Q.H.; Cao, G.H. Providing privacy-aware incentives for mobile sensing. In Proceedings of the 2013 IEEE International Conference on Pervasive Computing and Communications (PerCom), San Diego, CA, USA, 18–22 March 2013; pp. 76–84.
- Chen, J.; Zhang, H.L.; Du, X.J.; Fang, B.; Yan, L. Designing robust routing protocols to protect base stations in wireless sensor networks. J Wirel. Commun. Mob. Comput. 2014, 14, 1613–1626. [Google Scholar] [CrossRef]
- Ahmoud, M.M.; Shen, X. A cloud-based scheme for protecting source-location privacy against hotspot-locating attack in wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1805–1818. [Google Scholar] [CrossRef]
- Kanthakumar, P.; Xiao, L. Sensor node source privacy and packet recovery under eavesdropping and node compromise attacks. ACM Trans. Sens. Netw. 2013, 9. [Google Scholar] [CrossRef]
- Wang, W.P.; Chen, L.; Wang, J.X. A source-location privacy protocol in WSN based on locational angle. In Proceedings of the 2008 IEEE International Conference on Communications, Beijng, China, 19–23 May 2008; pp. 1630–1634.
- Mehta, K.; Liu, D.; Wright, M. Protecting location privacy in sensor networks against a global eavesdropper. IEEE Trans. Mob. Comput. 2012, 11, 320–336. [Google Scholar] [CrossRef]
- Yang, Y.; Shao, M.; Zhu, S.C.; Cao, G. Towards statistically strong source anonymity for sensor networks. ACM Trans. Sens. Netw. 2013, 9. [Google Scholar] [CrossRef]
- Cuellar, J.; Poovendran, R. Toward a Statistical Framework for Source Anonymity in Sensor Networks. IEEE Trans. Mob. Comput. 2013, 12, 248–260. [Google Scholar] [CrossRef]
- Rui, S.; Goswami, M.; Jie, G.; Gu, X. Is random walk truly memoryless—Traffic analysis and source location privacy under random walks. In Proceedings of the 2013 IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 3021–3029.
- Spachos, P.; Song, L.; Bui, F.M.; Hatzinakos, D. Improving source-location privacy through opportunistic routing in wireless sensor networks. In Proceedings of the 2011 IEEE Symposium on Computers and Communications (ISCC), Kerkyra, Greece, 28 June–1 July 2011; pp. 815–820.
- Spachos, P.; Toumpakaris, D.; Hatzinakos, D. Angle-based Dynamic Routing Scheme for Source Location Privacy in Wireless Sensor Networks. In Proceedings of the 2014 IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–5.
- Reed, M.; Syverson, P.; Goldschlag, D. Proxies for anonymous routing. In Proceedings of the 12th Annual Computer Security Applications Conference, San Diego, CA, USA, 9–13 December 1996; pp. 95–104.
- Reiter, M.; Rubin, A. Crowds: Anonymity for web transactions. Trans. Inf. Syst. Secur. (TISSEC) 1998, 1. [Google Scholar] [CrossRef]
- Chen, J.; Du, X.; Fang, B. An efficient anonymous communication protocol for wireless sensor networks. Wirel. Commun. Mob. Comput. 2011, 12. [Google Scholar] [CrossRef]
- Sheu, J.; Jiang, J.; Tu, C. Anonymous path routing in wireless sensor networks. In Proceedings of the 2008 IEEE International Conference on Communications, Beijing, China, 19–23 May 2008.
- Luo, X.; Ji, X.; Park, M. Location privacy against traffic analysis attacks in wireless sensor networks. In Proceedings of the 2010 International Conference on Information Science and Applications (ICISA), Seoul, Korea, 21–23 April 2010; pp. 1–6.
- Conti, M.; Willemsen, J.; Crispo, B. Providing source location privacy in wireless sensor networks: A survey. J. Commun. Surv. Tutor. 2013, 15, 1238–1280. [Google Scholar] [CrossRef]
- Kang, L. Protecting Location Privacy in Large-Scale Wireless Sensor Networks. In Proceedings of the 2009 IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–6.
- Dmitriev, A.S.; Efremova, E.V.; Gerasimo, M.Y. Multimedia sensor networks based on ultrawideband chaotic radio pulses. J. Commun. Technol. 2015, 60, 393–401. [Google Scholar] [CrossRef]
- Saleh, S.; Ahmed, M.; Ali, B.M.; Rasid, M.F.A.; Ismail, A. A survey on energy awareness mechanisms in routing protocols for wireless sensor networks using optimization methods. Trans. Emerg. Telecommun. Technol. 2014, 25. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Lin, Z.; Hu, Y.; Wang, B. Hiding the Source Based on Limited Flooding for Sensor Networks. Sensors 2015, 15, 29129-29148. https://doi.org/10.3390/s151129129
Chen J, Lin Z, Hu Y, Wang B. Hiding the Source Based on Limited Flooding for Sensor Networks. Sensors. 2015; 15(11):29129-29148. https://doi.org/10.3390/s151129129
Chicago/Turabian StyleChen, Juan, Zhengkui Lin, Ying Hu, and Bailing Wang. 2015. "Hiding the Source Based on Limited Flooding for Sensor Networks" Sensors 15, no. 11: 29129-29148. https://doi.org/10.3390/s151129129
APA StyleChen, J., Lin, Z., Hu, Y., & Wang, B. (2015). Hiding the Source Based on Limited Flooding for Sensor Networks. Sensors, 15(11), 29129-29148. https://doi.org/10.3390/s151129129