Figure 1.
(a) Structure of a common PIR detector; (b) layout of the Fresnel lenses array; (c) top view of the distribution of the SZs and NZs in each detection layer, where the sectors labeled by “+” indicate the PSZs, those labeled by “−“ indicate the NSZs and the gaps between the PSZs and NSZs indicate the BZs; (d) lateral view of the distribution of the three detector layers.
The Fresnel lenses array partitions the detector’s field of view (FOV) into a series of alternately distributed “sensitive zones” (SZs) and “blind zones” (BZs). Owing to the dual structure of the PIR sensor, the SZs are divided into positive SZs (PSZ) and negative SZs (NSZ) [
11]. If a thermal source goes from a PSZ into a NSZ, the polarity of sensor’s output will be reversed. Because of the three-row layout of the Fresnel lenses array, as shown
Figure 1b, the FOV of the PIR detector is accordingly divided into three detection layers, as shown in
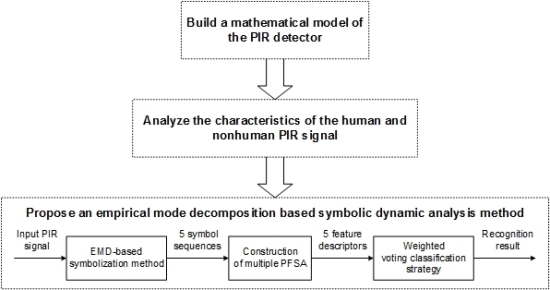
Figures 1c,d, each detection layer contains different number of SZs (or NZs). Because of the different heights and body shapes, the human and nonhuman targets would intersect with different detection layers when they cross the detector’s FOV. To find the relationship between the intersection pattern of the target and the characters of its PIR signals, we build a mathematical model of the PIR detector. When a PIR sensor is heated by a thermal source, it would generate a current signal that satisfies Equation (1) [
12,
13]:
where
t indicates the time instance,
p,
Cp and α indicate the pyroelectric coefficient, heat capacity and absorptivity of the sensitive element respectively,
T(
t),
As and
GTh separately indicate the temperature, surface area and thermal conductance of the PIR sensor,
u(t) is the unite step function,
is the convolution operator, and
Φ(
t) is the thermal power received by the PIR sensor. According to Liu’s study [
13], based on the Stefan-Boltzman law,
Φ(
t) can be simplified as Equation (2):
where
d0 indicates the distance between the thermal source and the PIR sensor,
kB indicates the emissivity of the thermal source,
εh is the Stefan-Boltzmann constant,
Ta and
Ts indicate the temperature of the ambient and the the thermal source respectively,
N(
t) is the thermal noise and
A(
t) is the surface area of the thermal sources that can be observed by the PIR sensor. In the PIR detector, because the infrared radiation coming from the PSZs would be offset by those coming from the NSZs [
11], A(
t) actually equals to the difference between the target’s surface area that exposes in the PSZs and that exposes in the NSZs,
i.e.,:
where
is the targets’ surface area that exposes in the
ith PSZ,
indicates the surface area that exposes in the
ith NSZ,
N is the number of the PSZs (or NSZs) in the entire FOV. Therefore, we can term
A(
t) as “net effective area” (NEA) and term its changing curve as the “NEA curve”.
Using the mathematical model elaborated above, we can simulate the generation process of the human and nonhuman PIR signals (taking an adult and a dog for instance) for analyzing their inherent differences. As shown in
Figure 2, because the detector’s FOV is divided into three detection layers by the Fresnel lenses array, according to the targets’ body shapes and the width of SZs and BZs [
7], we first calculate the “layer-NEA curves” of each target,
i.e., the changing curves of the surface area that exposes in each detective layer, rather than the entire FOV. We can see from
Figure 2 that, even in the same detection layer, the adult’s and dog’s layer-NEA curves still have different patterns, this is because the adult and dog have different body widths. Through adding the three layer-NEA curves together, we can obtain the targets’ NEA curves in the entire FOV. We can see from
Figure 2 that because the adult is much higher than the dog, he can intersect with more detection layers than a dog. Therefore, after adding the three layer-NEA curves together, the adult would generate a relatively complex NEA curve with many riding wives and small fluctuations, whereas the dog will generate a smoother one. Through substituting the NEA curves (
i.e.,
A(
t)) and another sensor’s parameters into Equations (1) and (2), we can obtain the simulated PIR signals.
Figure 2.
Simulation of the adult’s (a) and the dog’s (b) PIR signals, where the squares with the symbol “+” in the front view of FOV indicate the PSZs and those with the symbol “−“ indicate the NSZs, the blank between PSZ and NSZ indicates the PSZs.
Figure 3.
Real (blue-solid) and simulated (red-dashed) PIR signals of adult (a) and dog (b).