A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications
Abstract
:1. Introduction
2. Related Cycling Localization Techniques
3. Mobile Node System Model
3.1. Outdoor Experiment
3.2. Indoor Experiment
4. Soft Computing-Based Localization Techniques
4.1. ANFIS Techniques
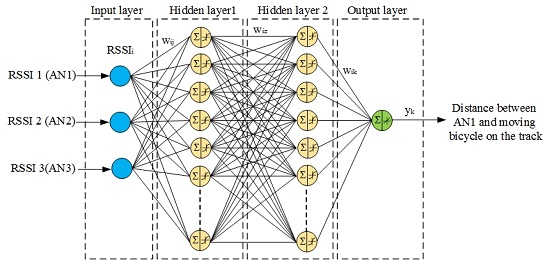
4.2. ANN Techniques
4.3. Heuristic Algorithms
5. Results and Discussion
5.1. ANFIS Techniques
5.2. Hybrid Heuristic Algorithms-ANN Techniques
6. Results Comparison
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- So-In, C.; Permpol, S.; Rujirakul, K. Soft computing-based localizations in wireless sensor networks. Pervasive Mob. Comput. 2016, 29, 17–37. [Google Scholar] [CrossRef]
- Zhang, T.; He, J.; Zhang, Y. Secure sensor localization in wireless sensor networks based on neural network. Int. J. Comput. Intell. Syst. 2012, 5, 914–923. [Google Scholar] [CrossRef]
- Blumrosen, G.; Hod, B.; Anker, T.; Dolev, D.; Rubinsky, B. Enhancing RSSI-based tracking accuracy in wireless sensor networks. ACM Trans. Sens. Netw. (TOSN) 2013, 9, 29. [Google Scholar] [CrossRef]
- Bhuvaneswari, P.; Vaidehi, V.; Saranya, M.A. Distance based transmission power control scheme for indoor wireless sensor network. In Transactions on Computational Science XI; Springer: Berlin, Germany, 2010; Volume 6480, pp. 207–222. [Google Scholar]
- Rossi, M.; Brunelli, D.; Adami, A.; Lorenzelli, L.; Menna, F.; Remondino, F. Gas-drone: Portable gas sensing system on UAVs for gas leakage localization. In Proceedings of the IEEE Sensors 2014, Valencia, Spain, 2–5 November 2014; pp. 1431–1434.
- Lo, G.; González-Valenzuela, S.; Leung, V.C.M. Wireless body area network node localization using small-scale spatial information. IEEE J. Biomed. Health Inform. 2013, 17, 715–726. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Xi, W.; He, Y.; Liu, Y.; Li, X.-Y.; Mo, L.; Yang, Z. Localization of wireless sensor networks in the wild: Pursuit of ranging quality. IEEE/ACM Trans. Netw. (TON) 2013, 21, 311–323. [Google Scholar] [CrossRef]
- Karim, L.; Nasser, N.; Mahmoud, Q.H.; Anpalagan, A.; Salti, T.E. Range-free localization approach for M2M communication system using mobile anchor nodes. J. Netw. Comput. Appl. 2015, 47, 137–146. [Google Scholar] [CrossRef]
- Gu, S.; Yue, Y.; Maple, C.; Wu, C. Fuzzy logic based localisation in wireless sensor networks for disaster environments. In Proceedings of the 18th International Conference on Automation and Computing (ICAC), Loughborough, UK, 7–8 September 2012; pp. 1–5.
- Payal, A.; Rai, C.; Reddy, B. Analysis of some feedforward artificial neural network training algorithms for developing localization framework in wireless sensor networks. Wirel. Pers. Commun. 2015, 82, 2519–2536. [Google Scholar] [CrossRef]
- Gu, Y.; Lo, A.; Niemegeers, I. A survey of indoor positioning systems for wireless personal networks. IEEE Commun. Surv. Tutor. 2009, 11, 13–32. [Google Scholar] [CrossRef]
- Tarrío, P.; Bernardos, A.M.; Casar, J.R. An energy-efficient strategy for accurate distance estimation in wireless sensor networks. Sensors 2012, 12, 15438–15466. [Google Scholar] [CrossRef] [PubMed]
- Robles, J.J. Indoor localization based on wireless sensor networks. AEU Int. J. Electron. Commun. 2014, 68, 578–580. [Google Scholar] [CrossRef]
- Wen, F.; Liang, C. Fine-grained indoor localization using single access point with multiple antennas. IEEE Sens. J. 2015, 15, 1538–1544. [Google Scholar]
- Xiong, H.; Chen, Z.; Yang, B.; Ni, R. TDoA localization algorithm with compensation of clock offset for wireless sensor networks. China Commun. 2015, 12, 193–201. [Google Scholar] [CrossRef]
- Maddumabandara, A.; Leung, H.; Liu, M. Experimental evaluation of indoor localization using wireless sensor networks. IEEE Sens.J. 2015, 15, 5228–5237. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, Y.H.; Pan, Q. Distributed, robust acoustic source localization in a wireless sensor network. IEEE Trans. Signal Process. 2012, 60, 4350–4359. [Google Scholar] [CrossRef]
- Chizari, H.; Poston, T.; Abd Razak, S.; Abdullah, A.H.; Salleh, S. Local coverage measurement algorithm in GPS-free wireless sensor networks. Ad Hoc Netw. 2014, 23, 1–17. [Google Scholar] [CrossRef]
- Pratap, K.S.; Eric, H.-K.W.; Jagruti, S. DuRT: Dual rssi trend based localization for wireless sensor networks. IEEE Sens. J. 2013, 13, 3115–3123. [Google Scholar]
- Pivato, P.; Palopoli, L.; Petri, D. Accuracy of RSS-based centroid localization algorithms in an indoor environment. IEEE Trans. Instrum. Meas. 2011, 60, 3451–3460. [Google Scholar] [CrossRef]
- Sugeno, M. An introductory survey of fuzzy control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Ma, D.; Er, M.J.; Wang, B. Analysis of hop-count-based source-to-destination distance estimation in wireless sensor networks with applications in localization. IEEE Trans. Veh. Technol. 2010, 59, 2998–3011. [Google Scholar]
- Cheng, L.; Wu, C.; Zhang, Y.; Wu, H.; Li, M.; Maple, C. A survey of localization in wireless sensor network. Int. J. Distrib. Sens. Netw. 2012, 2012, 12. [Google Scholar] [CrossRef]
- Zhao, L.-z.; Wen, X.-b.; Li, D. Amorphous localization algorithm based on BP artificial neural network. Int. J. Distrib. Sens. Netw. 2015, 2015, 6. [Google Scholar] [CrossRef]
- Lin, C.-M.; Mon, Y.-J.; Lee, C.-H.; Juang, J.-G.; Rudas, I.J. ANFIS-based indoor location awareness system for the position monitoring of patients. Acta Polytech. Hung. 2014, 11, 37–48. [Google Scholar]
- Velimirovic, A.S.; Djordjevic, G.L.; Velimirovic, M.M.; Jovanovic, M.D. Fuzzy ring-overlapping range-free (FRORF) localization method for wireless sensor networks. Comput. Commun. 2012, 35, 1590–1600. [Google Scholar] [CrossRef]
- Chagas, S.H.; Martins, J.B.; De Oliveira, L.L. An approach to localization scheme of wireless sensor networks based on artificial neural networks and genetic algorithms. In Proceedings of the IEEE 10th International New Circuits and systems Conference (NEWCAS), Montreal, QC, Canada, 17–20 June 2012; pp. 137–140.
- Liu, Z.-K.; Zhong, L. Node self-localization algorithm for wireless sensor networks based on modified particle swarm optimization. In Proceedings of the 27th IEEE Chinese Control and Decision Conference (CCDC), Qingdao, China, 23–25 May 2015; pp. 5968–5971.
- Kulkarni, R.V.; Venayagamoorthy, G.K. Bio-inspired algorithms for autonomous deployment and localization of sensor nodes. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 40, 663–675. [Google Scholar] [CrossRef]
- Krishnaprabha, R.; Gopakumar, A. Performance of gravitational search algorithm in wireless sensor network localization. In Proceedings of the National Conference on Communication, Signal Processing and Networking (NCCSN), Palakkad, India, 10–12 October 2014; pp. 1–6.
- Baca, A.; Kornfeind, P.; Preuschl, E.; Bichler, S.; Tampier, M.; Novatchkov, H. A server-based mobile coaching system. Sensors 2010, 10, 10640–10662. [Google Scholar] [CrossRef] [PubMed]
- Walker, W.; Praveen Aroul, A.L.; Bhatia, D. Mobile health monitoring systems. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Minneapolis, MN, USA, 2–6 September 2009; pp. 5199–5202.
- Eisenman, S.B.; Miluzzo, E.; Lane, N.D.; Peterson, R.A.; Ahn, G.-S.; Campbell, A.T. Bikenet: A mobile sensing system for cyclist experience mapping. ACM Trans. Sens. Netw. (TOSN) 2009, 6, 6. [Google Scholar] [CrossRef]
- Zhan, A.; Chang, M.; Chen, Y.; Terzis, A. Accurate caloric expenditure of bicyclists using cellphones. In Proceedings of the 10th ACM Conference on Embedded Network Sensor Systems, Toronto, Canada, 6–9 November 2012; pp. 71–84.
- Mi, Q.; Stankovic, J.A.; Stoleru, R. Practical and secure localization and key distribution for wireless sensor networks. Ad Hoc Netw. 2012, 10, 946–961. [Google Scholar] [CrossRef]
- Liebner, M.; Klanner, F.; Stiller, C. Active safety for vulnerable road users based on smartphone position data. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gold Coast, QLD, Australia, 23–26 June 2013; pp. 256–261.
- Liu, X.; Li, B.; Jiang, A.; Qi, S.; Xiang, C.; Xu, N. A bicycle-borne sensor for monitoring air pollution near roadways. In Proceedings of the IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Taipei, Tawan, 6–8 June 2015; pp. 166–167.
- Luoh, L. ZigBee-based intelligent indoor positioning system soft computing. Soft Comput. 2014, 18, 443–456. [Google Scholar] [CrossRef]
- Marita, T.; Negru, M.; Danescu, R.; Nedevschi, S. Stop-line detection and localization method for intersection scenarios. In Proceedings of the IEEE International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 25–27 August 2011; pp. 293–298.
- Nabil, M.; Ramadan, R.; ElShenawy, H.; ElHennawy, A. A comparative study of localization algorithms in WSNs. In Advanced Machine Learning Technologies and Applications; Hassanien, A., Salem, A.-B., Ramadan, R., Kim, T.-H., Eds.; Springer Berlin Heidelberg: Cario, Egypt, 2012; Volume 322, pp. 339–350. [Google Scholar]
- Pias, M.; Xu, K.; Hui, P.; Crowcroft, J.; Yang, G.-H.; Li, V.O.; Taherian, S. Sentient bikes for collecting mobility traces in opportunistic networks. In Proceedings of the 1st ACM International Workshop on Hot Topics of Planet-Scale Mobility Measurements, Kraków, Poland, 22–25 June 2009; p. 5.
- Shin, H.Y.; Un, F.L.; Huang, K.W. A sensor-based tracking system for cyclist group. In Proceedings of the Seventh International Conference on Complex, Intelligent, and Software Intensive Systems (CISIS), Taichung, Taiwan, 3–5 July 2013; pp. 617–622.
- Ndzi, D.L.; Harun, A.; Ramli, F.M.; Kamarudin, M.L.; Zakaria, A.; Shakaff, A.Y.M.; Jaafar, M.N.; Zhou, S.; Farook, R.S. Wireless sensor network coverage measurement and planning in mixed crop farming. Comput. Electron. Agric. 2014, 105, 83–94. [Google Scholar] [CrossRef] [Green Version]
- Aboelela, E.H.; Khan, A.H. Wireless sensors and neural networks for intruders detection and classification. In Proceedings of the International Conference on Information Networking (ICOIN), Bali, Indonesia, 1–3 February 2012; pp. 138–143.
- Kumar, S.; Jeon, S.M.; Lee, S.R. Localization estimation using artificial intelligence technique in wireless sensor networks. J. Korea Inf. Commun. Soc. 2014, 39, 820–827. [Google Scholar] [CrossRef]
- Jang, H.; Topal, E. A review of soft computing technology applications in several mining problems. Appl. Soft Comput. 2014, 22, 638–651. [Google Scholar] [CrossRef]
- Volosencu, C.; Curiac, D.-I. Efficiency improvement in multi-sensor wireless network based estimation algorithms for distributed parameter systems with application at the heat transfer. EURASIP J. Adv. Signal Process. 2013, 2013, 1–17. [Google Scholar] [CrossRef]
- Nekooei, S.M.; Manzuri-Shalmani, M.T. Location finding in wireless sensor network based on soft computing methods. In International Conference on Control, Automation and Systems Engineering (CASE), Singapore, 30–31 July 2011; 2011; pp. 1–5. [Google Scholar]
- Larios, D.; Barbancho, J.; Molina, F.J.; León, C. Lis: Localization based on an intelligent distributed fuzzy system applied to a WSN. Ad Hoc Net. 2012, 10, 604–622. [Google Scholar] [CrossRef]
- Oussalah, M.; Alakhras, M.; Hussein, M. Multivariable fuzzy inference system for fingerprinting indoor localization. Fuzzy Sets Syst. 2015, 269, 65–89. [Google Scholar] [CrossRef]
- Mona, Y.-J. WSN-based indoor location identification system (LIS) applied to vision robot designed by fuzzy neural network. J. Digit. Inf. Manag. 2015, 13, 37. [Google Scholar]
- Palipana, S.; Kapukotuwe, C.; Malasinghe, U.; Wijenayaka, P.; Munasinghe, S. Localization of a mobile robot using ZigBee based optimization techniques. In Proceedings of the IEEE 6th International Conference on Information and Automation for Sustainability (ICIAfS), Beijing, China, 27–29 September 2012; pp. 215–220.
- Gholami, M.; Cai, N.; Brennan, R.W. An artificial neural network approach to the problem of wireless sensors network localization. Robot. Comput. Integr. Manuf. 2013, 29, 96–109. [Google Scholar] [CrossRef]
- Payal, A.; Rai, C.; Reddy, B. Artificial neural networks for developing localization framework in wireless sensor networks. In Proceedings of the International Conference on Data Mining and Intelligent Computing (ICDMIC), New Delhi, India, 5–6 September 2014; pp. 1–6.
- Kukolj, D.; Levi, E. Identification of complex systems based on neural and takagi-sugeno fuzzy model. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 272–282. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mansouri, R.; Nasseri, F.; Khorrami, M. Effective time variation of G in a model universe with variable space dimension. Phys. Lett. A 1999, 259, 194–200. [Google Scholar] [CrossRef]
- Shuaib, Y.M.; Kalavathi, M.S.; Rajan, C.C.A. Optimal capacitor placement in radial distribution system using gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 384–397. [Google Scholar] [CrossRef]
- Chatterjee, A.; Roy, K.; Chatterjee, D. A gravitational search algorithm (GSA) based photo-voltaic (PV) excitation control strategy for single phase operation of three phase wind-turbine coupled induction generator. Energy 2014, 74, 707–718. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, S.R. Localization with RSSI values for wireless sensor networks: An artificial neural network approach. In Proceedings of the 1st International Electronic Conference on Sensors and Applications 1, Seoul, Korea, 1–16 June 2014; pp. 1–6.
- Chuang, P.-J.; Jiang, Y.-J. Effective neural network-based node localisation scheme for wireless sensor networks. IET Wirel. Sens. Syst. 2014, 4, 97–103. [Google Scholar] [CrossRef]
- Nanda, M.; Kumar, A.; Kumar, S. Localization of 3D WSN using mamdani sugano fuzzy weighted centriod approaches. In Proceedings of the IEEE Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 1–2 March 2012; pp. 1–5.
- Feng, X.; Gao, Z.; Yang, M.; Xiong, S. Fuzzy distance measuring based on RSSI in wireless sensor network. In Proceedings of the 3rd International Conference on Intelligent System and Knowledge Engineering, Xiamen, China, 17–19 November 2008; pp. 395–400.
- Yun, S.; Lee, J.; Chung, W.; Kim, E.; Kim, S. A soft computing approach to localization in wireless sensor networks. Expert Syst. Appl. 2009, 36, 7552–7561. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, Y.; Zhang, J.; Liu, Y. Research of self-calibration location algorithm for ZigBee based on pso-rssi. In Electronics and Signal Processing; Springer: Berlin, Germany, 2011; pp. 91–99. [Google Scholar]
- Gharghan, S.K.; Nordin, R.; Ismail, M.; Ali, J.A. Accurate wireless sensor localization technique based on hybrid PSO-ANN algorithm for indoor and outdoor track cycling. IEEE Sens. J. 2016, 16, 529–541. [Google Scholar] [CrossRef]
- Tewolde, G.S.; Kwon, J. Efficient WiFi-based indoor localization using particle swarm optimization. In Advances in Swarm Intelligence; Springer: Berlin, Germany, 2011; pp. 203–211. [Google Scholar]
- Brunato, M.; Battiti, R. Statistical learning theory for location fingerprinting in wireless LANS. Comput. Netw. 2005, 47, 825–845. [Google Scholar] [CrossRef]
- Mestre, P.; Coutinho, L.; Reigoto, L.; Matias, J.; Correia, A.; Couto, P.; Serodio, C. Indoor location using fingerprinting and fuzzy logic. In Eurofuse 2011; Springer: Berlin, Germany, 2011; pp. 363–374. [Google Scholar]
- Nerguizian, C.; Nerguizian, V. Indoor fingerprinting geolocation using wavelet-based features extracted from the channel impulse response in conjunction with an artificial neural network. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Vigo, Spain, 4–7 June 2007; pp. 2028–2032.
- Azenha, A.; Peneda, L.; Carvalho, A. A neural network approach for radio frequency based indoors localization. In Proceedings of the IECON 38th Annual Conference on Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5990–5995.
- Wu, B.-F.; Jen, C.-L.; Chang, K.-C. Neural fuzzy based indoor localization by kalman filtering with propagation channel modeling. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics (ISIC), Montreal, QC, Canada, 7–10 October 2007; pp. 812–817.
- Irfan, N.; Bolic, M.; Yagoub, M.C.; Narasimhan, V. Neural-based approach for localization of sensors in indoor environment. Telecommun. Syst. 2010, 44, 149–158. [Google Scholar] [CrossRef]
- Rahman, M.S.; Park, Y.; Kim, K.-D. RSS-based indoor localization algorithm for wireless sensor network using generalized regression neural network. Arab. J. Sci. Eng. 2012, 37, 1043–1053. [Google Scholar] [CrossRef]
- Moreno-Cano, M.; Zamora-Izquierdo, M.A.; Santa, J.; Skarmeta, A.F. An indoor localization system based on artificial neural networks and particle filters applied to intelligent buildings. Neurocomputing 2013, 122, 116–125. [Google Scholar] [CrossRef]
- Brás, L.; Pinho, P.; Borges Carvaloh, N. Evaluation of a sectorised antenna in an indoor localisation system. IET Microw. Antennas Propag. 2013, 7, 679–685. [Google Scholar] [CrossRef]
- Thongpul, K.; Jindapetch, N.; Teerapakajorndet, W. A neural network based optimization for wireless sensor node position estimation in industrial environments. In Proceedings of the International Conference on Electrical Engineering/Electronics Computer Telecommunications and Information Technology (ECTI-CON), Chaing Mai, Thailand, 19–21 May 2010; pp. 249–253.
- Gogolak, L.; Pletl, S.; Kukolj, D. Indoor fingerprint localization in WSN environment based on neural network. In Proceedings of the IEEE 9th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 8–10 September 2011; pp. 293–296.




















| Parameter | PSO | GSA | BSA |
|---|---|---|---|
| Population size 3 | 10, 20, 30, 40, and 50 | 10, 20, 30, 40, and 50 | 10, 20, 30, 40, and 50 |
| Iteration | 100 | 100 | 100 |
| c1 and c2 | 1.494 | - | - |
| w | 0.7 | - | - |
| F | - | - | 3 |
| G0 and α | - | 1, 0.2 | - |
| ANFIS Method | Outdoor | Indoor | ||
|---|---|---|---|---|
| MAE (m) | RMSE (m) | MAE (m) | RMSE (m) | |
| 3 trimf | 2.486 | 3.938 | 3.581 | 4.725 |
| 5 trimf | 1.588 | 2.647 | 1.91 | 3.05 |
| 7 trimf | 0.3634 | 0.907 | 1.004 | 2.107 |
| 3 gbellmf | 2.335 | 3.713 | 2.927 | 3.978 |
| 5 gbellmf | 0.4695 | 0.796 | 1.4269 | 2.476 |
| 7 gbellmf | 0.022 | 0.062 | 0.284 | 1.108 |
| Population Size | Parameters | GSA-ANN | PSO-ANN | BSA-ANN | |||
|---|---|---|---|---|---|---|---|
| Outdoor | Indoor | Outdoor | Indoor | Outdoor | Indoor | ||
| 10 | N1 | 19 | 15 | 12 | 9 | 14 | 11 |
| N2 | 19 | 17 | 18 | 16 | 19 | 18 | |
| LR | 0.2541 | 0.3429 | 0.1877 | 0.4477 | 0.2505 | 0.6652 | |
| 20 | N1 | 17 | 10 | 18 | 7 | 10 | 15 |
| N2 | 17 | 16 | 16 | 18 | 19 | 18 | |
| LR | 0.8004 | 0.7394 | 0.0709 | 0.5864 | 0.3492 | 0.223 | |
| 30 | N1 | 6 | 14 | 17 | 14 | 15 | 15 |
| N2 | 12 | 11 | 18 | 14 | 19 | 19 | |
| LR | 0.5864 | 0.4764 | 0.4533 | 0.5027 | 0.8871 | 0.6608 | |
| 40 | N1 | 18 | 10 | 17 | 15 | 17 | 8 |
| N2 | 16 | 14 | 16 | 16 | 17 | 17 | |
| LR | 0.5947 | 0.5152 | 0.6127 | 0.4206 | 0.7139 | 0.9743 | |
| 50 | N1 | 14 | 13 | 11 | 16 | 16 | 17 |
| N2 | 13 | 10 | 18 | 19 | 18 | 19 | |
| LR | 0.5487 | 0.535 | 0.9407 | 0.7194 | 0.4737 | 0.4655 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharghan, S.K.; Nordin, R.; Ismail, M. A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications. Sensors 2016, 16, 1043. https://doi.org/10.3390/s16081043
Gharghan SK, Nordin R, Ismail M. A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications. Sensors. 2016; 16(8):1043. https://doi.org/10.3390/s16081043
Chicago/Turabian StyleGharghan, Sadik Kamel, Rosdiadee Nordin, and Mahamod Ismail. 2016. "A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications" Sensors 16, no. 8: 1043. https://doi.org/10.3390/s16081043
APA StyleGharghan, S. K., Nordin, R., & Ismail, M. (2016). A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications. Sensors, 16(8), 1043. https://doi.org/10.3390/s16081043