Autonomous Underwater Navigation and Optical Mapping in Unknown Natural Environments
Abstract
:1. Introduction
2. Path Planning Pipeline
2.1. Module for Incremental and Online Mapping
2.2. Module for (Re)Planning Paths Online
2.2.1. Anytime Approach for (Re)Planning Online
| Algorithm 1: buildRRT |
| Input: T: tree of collision-free configurations.  |
| Algorithm 2: extendRRT* |
| Input: T: tree of collision-free configurations. : state towards which the tree will be extended. : C-Space. Output: Result after attempting to extend.  |
2.2.2. Delayed Collision Checking for (Re)Planning Incrementally and Online
2.3. Mission Handler
2.4. Conducting Surveys at a Desired Distance Using a C-Space Costmap
3. 3D Reconstruction Pipeline
3.1. Keyframe Selection
3.2. Color Correction
3.3. Distortion Correction
3.4. Sparse Reconstruction
3.4.1. Feature Detection and Matching
3.4.2. Structure from Motion
3.5. Dense Reconstruction
3.6. Surface Reconstruction
3.7. Surface Texturing
4. Results
4.1. Experimental Setup and Simulation Environment
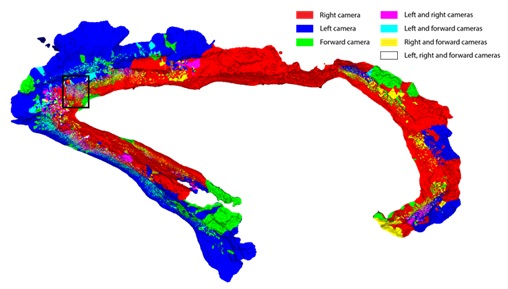
4.2. Online Mapping and Path Planning in Unexplored Natural Environments
4.3. 3D Reconstruction
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| C-Space | configuration space |
| RRT | rapidly-exploring random tree |
| RRT* | asymptotic optimal RRT |
| 1D | 1-dimensional |
| 2D | 2-dimensional |
| 3D | 3-dimensional |
| OMPL | open motion planning library |
| DFS | depth-first search |
| DOF | degrees of freedom |
| ROS | robot operating system |
| UUV | unmanned underwater vehicle |
| ROV | remotely operated vehicle |
| AUV | autonomous underwater vehicle |
| DVL | Doppler velocity log |
| IMU | inertial measurement unit |
| CIRS | underwater vision and robotics research center |
| COLA2 | component oriented layer-based architecture for autonomy |
| UWSim | underwater simulator |
| SIFT | scale-invariant feature transform |
| SfM | structure from motion |
| DOG | difference of Gaussians |
| RANSAC | random sample consensus |
| AC-RANSAC | a contrario-RANSAC |
| GPU | graphics processing unit |
| CAD | computer-aided design |
References
- Dunbabin, M.; Marques, L. Robots for environmental monitoring: Significant advancements and applications. IEEE Robot. Autom. Mag. 2012, 19, 24–39. [Google Scholar] [CrossRef]
- Whitcomb, L. Underwater robotics: out of the research laboratory and into the field. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 709–716.
- Pathak, K.; Birk, A.; Vaskevicius, N. Plane-based registration of sonar data for underwater 3D mapping. In Proceedings of the 2010 IEEE/RSJ International Conference onIntelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 4880–4885.
- Hurtós, N.; Cufí, X.; Salvi, J. Calibration of optical camera coupled to acoustic multibeam for underwater 3D scene reconstruction. In Proceedings of the OCEANS 2010 IEEE-Sydney, Sydney, Australia, 24–27 May 2010; pp. 1–7.
- Coiras, E.; Petillot, Y.; Lane, D.M. Multiresolution 3-D reconstruction from side-scan sonar images. IEEE Trans. Image Process. 2007, 16, 382–390. [Google Scholar] [CrossRef] [PubMed]
- Gracias, N.; Ridao, P.; Garcia, R.; Escartin, J.; L’Hour, M.; Cibecchini, F.; Campos, R.; Carreras, M.; Ribas, D.; Palomeras, N.; et al. Mapping the Moon: Using a lightweight AUV to survey the site of the 17th century ship ‘La Lune’. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–14 June 2013; pp. 1–8.
- Campos, R.; Garcia, R.; Alliez, P.; Yvinec, M. A surface reconstruction method for in-detail underwater 3D optical mapping. Int. J. Robot. Res. 2014, 34, 64–89. [Google Scholar]
- Massot-Campos, M.; Oliver-Codina, G. Optical Sensors and Methods for Underwater 3D Reconstruction. Sensors 2015, 15, 31525–31557. [Google Scholar] [CrossRef] [PubMed]
- Clarke, M.E.; Tolimieri, N.; Singh, H. Using the seabed AUV to assess populations of groundfish in untrawlable areas. In The future of fisheries science in North America; Springer: Dordrecht, The Netherlands, 2009; pp. 357–372. [Google Scholar]
- Grasmueck, M.; Eberli, G.P.; Viggiano, D.A.; Correa, T.; Rathwell, G.; Luo, J. Autonomous underwater vehicle (AUV) mapping reveals coral mound distribution, morphology, and oceanography in deep water of the Straits of Florida. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Smale, D.A.; Kendrick, G.A.; Harvey, E.S.; Langlois, T.J.; Hovey, R.K.; Van Niel, K.P.; Waddington, K.I.; Bellchambers, L.M.; Pember, M.B.; Babcock, R.C.; et al. Regional-scale benthic monitoring for ecosystem-based fisheries management (EBFM) using an autonomous underwater vehicle (AUV). ICES J. Marine Sci. J. Cons. 2012, 69. [Google Scholar] [CrossRef]
- Yoerger, D.R.; Jakuba, M.; Bradley, A.M.; Bingham, B. Techniques for deep sea near bottom survey using an autonomous underwater vehicle. Int. J. Robot. Res. 2007, 26, 41–54. [Google Scholar] [CrossRef]
- Barreyre, T.; Escartín, J.; Garcia, R.; Cannat, M.; Mittelstaedt, E.; Prados, R. Structure, temporal evolution, and heat flux estimates from the Lucky Strike deep-sea hydrothermal field derived from seafloor image mosaics. Geochem. Geophys. Geosyst. 2012, 13. [Google Scholar] [CrossRef]
- Yoerger, D.R.; Bradley, A.M.; Walden, B.B.; Cormier, M.H.; Ryan, W.B. Fine-scale seafloor survey in rugged deep-ocean terrain with an autonomous robot. In Proceedings of the ICRA’00 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 1787–1792.
- Bruno, F.; Gallo, A.; De Filippo, F.; Muzzupappa, M.; Petriaggi, B.D.; Caputo, P. 3D documentation and monitoring of the experimental cleaning operations in the underwater archaeological site of Baia (Italy). In Proceedings of the IEEE Digital Heritage International Congress (DigitalHeritage), Marseille, France, 28 October–1 November 2013; Volume 1, pp. 105–112.
- Eric, M.; Kovacic, R.; Berginc, G.; Pugelj, M.; Stopinšek, Z.; Solina, F. The impact of the latest 3D technologies on the documentation of underwater heritage sites. In Proceedings of the IEEE Digital Heritage International Congress (DigitalHeritage), Marseille, France, 28 October–1 November 2013; Volume 2, pp. 281–288.
- Shihavuddin, A.; Gracias, N.; Garcia, R.; Gleason, A.C.R.; Gintert, B. Image-Based Coral Reef Classification and Thematic Mapping. Remote Sens. 2013, 5, 1809–1841. [Google Scholar] [CrossRef]
- Beijbom, O.; Edmunds, P.J.; Kline, D.I.; Mitchell, B.G.; Kriegman, D. Automated annotation of coral reef survey images. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1170–1177.
- Shihavuddin, A.; Gracias, N.; Garcia, R.; Escartin, J.; Pedersen, R. Automated classification and thematic mapping of bacterial mats in the North Sea. In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Norway, 10–14 June 2013.
- Bewley, M.; Douillard, B.; Nourani-Vatani, N.; Friedman, A.; Pizarro, O.; Williams, S. Automated species detection: An experimental approach to kelp detection from sea-floor AUV images. In Proceedings of the Australasian Conference on Robotics & Automation, Wellington, New Zealand, 3–5 December 2012.
- Bryson, M.; Johnson-Roberson, M.; Pizarro, O.; Williams, S. Automated registration for multi-year robotic surveys of marine benthic habitats. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 3344–3349.
- Delaunoy, O.; Gracias, N.; Garcia, R. Towards Detecting Changes in Underwater Image Sequences. In Proceedings of the OCEANS 2008-MTS/IEEE Kobe Techno-Ocean, Kobe, Japan, 8–11 April 2008; pp. 1–8.
- Galceran, E.; Campos, R.; Palomeras, N.; Ribas, D.; Carreras, M.; Ridao, P. Coverage Path Planning with Real-time Replanning and Surface Reconstruction for Inspection of Three-dimensional Underwater Structures using Autonomous Underwater Vehicles. J. Field Robot. 2014, 32, 952–983. [Google Scholar] [CrossRef]
- Mallios, A.; Ridao, P.; Ribas, D.; Carreras, M.; Camilli, R. Toward autonomous exploration in confined underwater environments. J. Field Robot. 2015, 7. [Google Scholar] [CrossRef]
- Hernández, J.D.; Vidal, E.; Vallicrosa, G.; Galceran, E.; Carreras, M. Online path planning for autonomous underwater vehicles in unknown environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1152–1157.
- Hernández, J.D.; Istenic, K.; Gracias, N.; García, R.; Ridao, P.; Carreras, M. Autonomous Seabed Inspection for Environmental Monitoring. In ROBOT2015: Second Iberian Robotics Conference; Reis, L.P., Moreira, A.P., Lima, P.U., Montano, L., Muñoz-Martinez, V., Eds.; Springer International Publishing: Lisbon, Portugal, 2016; pp. 27–39. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Autonom. Robots 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Incremental Sampling-based Algorithms for Optimal Motion Planning. In Proceedings of the Robotics: Science and Systems (RSS), Zaragoza, Spain, 27–30 June 2010.
- Karaman, S.; Walter, M.R.; Perez, A.; Frazzoli, E.; Teller, S. Anytime Motion Planning using the RRT*. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1478–1483.
- Bekris, K.E.; Kavraki, L.E. Greedy but Safe Replanning under Kinodynamic Constraints. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Roma, Italy, 10–14 April 2007; pp. 704–710.
- Bohlin, R.; Kavraki, L.E. Path planning using lazy PRM. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 521–528.
- Elibol, A.; Gracias, N.; Garcia, R. Fast topology estimation for image mosaicing using adaptive information thresholding. Robot. Auton. syst. 2013, 61, 125–136. [Google Scholar] [CrossRef]
- Prados, R.; Garcia, R.; Gracias, N.; Escartin, J.; Neumann, L. A novel blending technique for underwater gigamosaicing. IEEE J. Ocean. Eng. 2012, 37, 626–644. [Google Scholar] [CrossRef]
- Singh, H.; Howland, J.; Pizarro, O. Advances in large-area photomosaicking underwater. IEEE J. Ocean. Eng. 2004, 29, 872–886. [Google Scholar] [CrossRef]
- Szeliski, R. Image mosaicing for tele-reality applications. In Proceedings of the Second IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; pp. 44–53.
- Ferrer, J.; Elibol, A.; Delaunoy, O.; Gracias, N.; Garcia, R. Large-area photo-mosaics using global alignment and navigation data. In Proceedings of the MTS/IEEE OCEANS Conference, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–9.
- Nicosevici, T.; Gracias, N.; Negahdaripour, S.; Garcia, R. Efficient three-dimensional scene modeling and mosaicing. J. Field Robot. 2009, 26, 759–788. [Google Scholar] [CrossRef]
- Campos, R.; Gracias, N.; Ridao, P. Underwater Multi-Vehicle Trajectory Alignment and Mapping Using Acoustic and Optical Constraints. Sensors 2016, 16, 387. [Google Scholar] [CrossRef] [PubMed]
- Garcia, R.; Campos, R.; Escartın, J. High-resolution 3D reconstruction of the seafloor for environmental monitoring and modelling. In Proceedings of the IROS Workshop on Robotics for Environmental Monitoring, San Francisco, CA, USA, 25–30 September 2011.
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Cavan, N. Reconstruction of 3D Points from Uncalibrated Underwater Video. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, April 2011. [Google Scholar]
- Bouguet, J.Y. Pyramidal Implementation of the Affine Lucas Kanade Feature Tracker Description of the Algorithm; Intel Corporation: Santa Clara, CA, USA, 2001; Volume 5, p. 4. [Google Scholar]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’94), Seattle, WA , USA, 21–23 June 1994; pp. 593–600.
- Bryson, M.; Johnson-Roberson, M.; Pizarro, O.; Williams, S.B. True Color Correction of Autonomous Underwater Vehicle Imagery. J. Field Robot. 2015. [Google Scholar] [CrossRef]
- Bianco, G.; Gallo, A.; Bruno, F.; Muzzupappa, M. A comparison between active and passive techniques for underwater 3D applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 357–363. [Google Scholar] [CrossRef]
- Jaffe, J.S. Computer modeling and the design of optimal underwater imaging systems. IEEE J. Ocean. Eng. 1990, 15, 101–111. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, USA, 1994. [Google Scholar]
- Andono, P.N.; Purnama, I.; Hariadi, M. Underwater Image Enhancement Using Adaptive Filtering for Enhanced Sift-Based Image Matching. Available online: http://www.jatit.org/volumes/Vol51No3/7Vol51No3.pdf (accessed on 1 October 2015).
- Ruderman, D.L.; Cronin, T.W.; Chiao, C.C. Statistics of cone responses to natural images: Implications for visual coding. J. Opt. Soc. Am. A 1998, 15, 2036–2045. [Google Scholar] [CrossRef]
- Treibitz, T.; Schechner, Y.Y.; Kunz, C.; Singh, H. Flat refractive geometry. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 51–65. [Google Scholar] [CrossRef] [PubMed]
- Gawlik, N. 3D Modelling of Underwater Archaeological Artefacts; Institutt for bygg, anlegg og transport: Trondheim, Trondheim, 2014. [Google Scholar]
- Kwon, Y.H. Object plane deformation due to refraction in two-dimensional underwater motion analysis. J. Appl. Biomech. 2010, 15, 396–403. [Google Scholar]
- Wu, C. Critical configurations for radial distortion self-calibration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 25–32.
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 1 October 2015).
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In Vision Algorithms: Theory and Practice; Springer: Heidelberg, Germany, 1999; pp. 298–372. [Google Scholar]
- Wu, C. SiftGPU: A GPU Implementation of Scale Invariant Feature Transform (SIFT). Available online: http://www.cs.unc.edu/~ccwu/siftgpu/ (accessed on 12 October 2015).
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2548–2555.
- Fischler, M.A.; Bolles, R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Moisan, L.; Moulon, P.; Monasse, P. Automatic homographic registration of a pair of images, with a contrario elimination of outliers. Image Process. On Line 2012, 2, 56–73. [Google Scholar] [CrossRef]
- La Bibliothèque OpenMVG: Open Source Multiple View Geometry. Available online: https://hal.archives-ouvertes.fr/hal-00829332/file/04.pdf (accessed on 21 September 2015).
- Moulon, P.; Monasse, P.; Marlet, R. Adaptive structure from motion with a contrario model estimation. In Computer Vision—ACCV 2012; Springer: Heidelberg, Germany, 2012; pp. 257–270. [Google Scholar]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F.; Gonizzi-Barsanti, S. Dense image matching: Comparisons and analyses. In Proceedings of the IEEE Digital Heritage International Congress (DigitalHeritage), Marseille, France, 28 October–1 November 2013; Volume 1, pp. 47–54.
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: London, UK, 2010. [Google Scholar]
- Ahmadabadian, A.H.; Robson, S.; Boehm, J.; Shortis, M.; Wenzel, K.; Fritsch, D. A comparison of dense matching algorithms for scaled surface reconstruction using stereo camera rigs. ISPRS J. Photogramm. Remote Sens. 2013, 78, 157–167. [Google Scholar] [CrossRef]
- Dall’Asta, E.; Roncella, R. A comparison of semiglobal and local dense matching algorithms for surface reconstruction. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 187–194. [Google Scholar] [CrossRef]
- Hirschmüller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Pierrot-Deseilligny, M.; Paparoditis, N. A multiresolution and Optimization-Based Image Matching Approach: An Application to Surface Reconstruction from SPOT5-HRS Stereo Imagery. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.4955&rep=rep1&type=pdf (accessed on 1 October 2015).
- Pierrot-Deseilligny, M.; De Luca, L.; Remondino, F. Automated image-based procedures for accurate artifacts 3D modeling and orthoimage generation. Geoinform. FCE CTU 2011, 6, 291–299. [Google Scholar] [CrossRef]
- Pierrot-Deseilligny, M.P. MicMac, Un Logiciel Pour La Mise En Correspondance Automatique D’images Dans Le Contexte Géographique. Available online: http://logiciels.ign.fr/IMG/pdf/Bulletin-Info-IGPN-2007.pdf (accessed on 15 October 2015).
- Roy, S.; Cox, I.J. A maximum-flow formulation of the n-camera stereo correspondence problem. In Proceedings of the 6th International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 492–499.
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. In Proceedings of the 4th Eurographics Symposium on Geometry Processing, Sardinia, Italy, 26–28 June 2006; Volume 7.
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. (TOG) 2013, 32, 29. [Google Scholar] [CrossRef]
- Campos, R.; Garcia, R.; Nicosevici, T. Surface reconstruction methods for the recovery of 3D models from underwater interest areas. In Proceedings of the IEEE OCEANS, Santander, Spain, 6–9 June 2011.
- Waechter, M.; Moehrle, N.; Goesele, M. Let there be color! Large-scale texturing of 3D reconstructions. In Computer Vision–ECCV; Springer: Cham, Switzerland, 2014; pp. 836–850. [Google Scholar]
- Fuhrmann, S.; Langguth, F.; Moehrle, N.; Waechter, M.; Goesele, M. MVE—An image-based reconstruction environment. Comput. Graph. 2015, 53, 44–53. [Google Scholar] [CrossRef]
- Pérez, P.; Gangnet, M.; Blake, A. Poisson image editing. ACM Trans. Graph. (TOG) 2003, 22, 313–318. [Google Scholar] [CrossRef]
- CIRS: Girona Underwater Vision and Robotics. Available online: http://cirs.udg.edu/ (accessed 2015–2016).
- Palomeras, N.; El-Fakdi, A.; Carreras, M.; Ridao, P. COLA2: A Control Architecture for AUVs. IEEE J. Ocean. Eng. 2012, 37, 695–716. [Google Scholar] [CrossRef]
- Prats, M.; Perez, J.; Fernandez, J.J.; Sanz, P.J. An open source tool for simulation and supervision of underwater intervention missions. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 2577–2582.
- Sucan, I.A.; Moll, M.; Kavraki, L.E. The Open Motion Planning Library. IEEE Robot. Autom. Mag. 2012, 19, 72–82. [Google Scholar] [CrossRef]
- Google Maps 2016. Sant Feliu de Guíxols, Girona, Spain 41°46’55.4"N, 3°02’55.1"E. Rocky Formation. Available online: https://www.google.es/maps/ (accessed on 2 May 2016).




















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández, J.D.; Istenič, K.; Gracias, N.; Palomeras, N.; Campos, R.; Vidal, E.; García, R.; Carreras, M. Autonomous Underwater Navigation and Optical Mapping in Unknown Natural Environments. Sensors 2016, 16, 1174. https://doi.org/10.3390/s16081174
Hernández JD, Istenič K, Gracias N, Palomeras N, Campos R, Vidal E, García R, Carreras M. Autonomous Underwater Navigation and Optical Mapping in Unknown Natural Environments. Sensors. 2016; 16(8):1174. https://doi.org/10.3390/s16081174
Chicago/Turabian StyleHernández, Juan David, Klemen Istenič, Nuno Gracias, Narcís Palomeras, Ricard Campos, Eduard Vidal, Rafael García, and Marc Carreras. 2016. "Autonomous Underwater Navigation and Optical Mapping in Unknown Natural Environments" Sensors 16, no. 8: 1174. https://doi.org/10.3390/s16081174
APA StyleHernández, J. D., Istenič, K., Gracias, N., Palomeras, N., Campos, R., Vidal, E., García, R., & Carreras, M. (2016). Autonomous Underwater Navigation and Optical Mapping in Unknown Natural Environments. Sensors, 16(8), 1174. https://doi.org/10.3390/s16081174