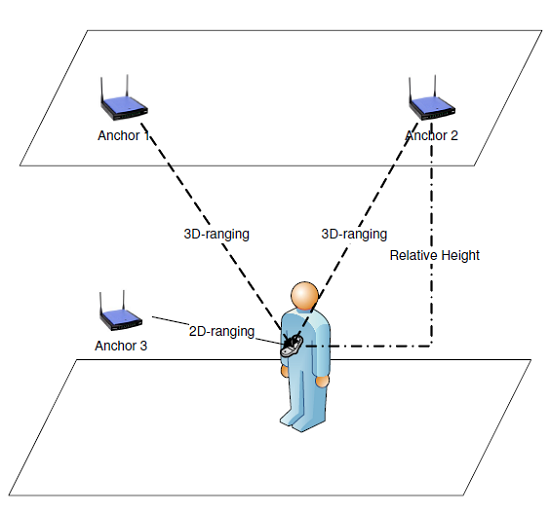
1. Introduction
Locating a target using a wireless sensor network (WSN) is an efficient way to support multiple Internet of Things (IoT) applications, and many measurement and sensing techniques are proposed [
1]. The techniques of measurement, such as angle-of-arrival (AOA), time-of-arrival (TOA), time-difference-of-arrival (TDOA) and received-signal-strength (RSS), play important roles in many applications, e.g., navigation, localization, target tracking and location-based service for mobile communication [
2,
3]. Just like other wireless applications, localization systems are sensitive to the signal noise. The major sources that influence the measurements result from the multi-path effect and non-line-of-sight (NLOS) during the propagation of the wireless signal due to the complicated infrastructures or environment. In addition, motivated by cloud computing and urban sensing technologies, multiple sensors are deployed widely, and much information in the complicated environment is also useful to calibrate the target position, e.g., map information and the trajectory records.
The main purpose of the localization system is the position estimation accuracy for a better location-based service. Thus, many research efforts focus on developing accurate location estimation algorithms [
4]. The key idea is to fuse multiple pieces of information, derive the relationship to the target position and eliminate the error. The most popular tools are the nonlinear filters based on the recursive Bayesian estimation model, e.g., extended Kalman filters, particle filters and Gaussian filters, which fuse the prior information of the previous state and the current measurement data to derive positions [
5,
6,
7]. One important factor that may influence the target position estimation is the NLOS signals. Thus, many algorithms try to identify the NLOS measurements and mitigate or adapt them based on the prior knowledge to improve the position estimation [
8,
9]. A hybrid method that combines the recursive Bayesian model and NLOS information is proposed according to the jump Markov model estimation [
10]. Multiple information fusion methods are also studied, which fuse both TOA and RSS measurements to improve the estimation [
11,
12]. The map or building layout information is also modeled for the wireless localization system and is applied for estimation [
13,
14]. It can be found that with the development of the sensing technique, more and more information will be integrated into the sensors and used for localization in the future. Thus, the localization system requires a scalable architecture to fuse such information. Although the indoor localization system is designed via employing multiple pieces of information, a theoretical analysis for such heterogeneous information is not provided yet.
Before the practical implementation of the WSN localization system, theoretical analysis is also required to evaluate the performance of the heterogeneous information fusion. The Cramér–Rao lower bound (CRLB) as the optimal performance indicator for the unbiased estimator is widely applied in localization and positioning systems. Theoretical investigations have been researched as the nonlinear problem for wireless localization systems. Tichavsky et al. provided the formulation of recursive posterior CRLB for nonlinear filters based on the Bayesian framework [
15]. Zuo et al. proposed a conditional CRLB, which considered that the posterior probability is conditioned on the prior probability [
16]. For range-based wireless localization system, many research works have provided CRLB results for different scenarios. A generalized CRLB (G-CRLB) of the wireless system is proposed for the NLOS environment [
17]. The hybrid LOS/NLOS environment is analyzed, and the authors indicated that with prior knowledge of the wireless transmission channel, the estimation performance can be improved [
17]. Shen et al. defined an equivalent CRLB (E-CRLB) for a general framework of the wideband wireless network [
18]. The multi-path and NLOS effect are both considered, and the CRLB with or without prior information is compared to the E-CRLB [
18]. A linear CRLB (L-CRLB) is proposed, which considers the linearized effect and provided the lower bound for such an estimator [
19]. Other similar works also give CRLB for different ranging techniques [
20,
21]. Although some other methods can be used for performance analysis [
22], CRLB is still popular for wireless localization researchers due to its simplicity and general expression. Although the above-mentioned CRLBs try to provide the general fundamental limits of the localization systems, they assume only parts of the factors in the localization problem, which limit their applications. In this case, these CRLBs still cannot be analyzed precisely since more information makes the environment complicated, and they are influenced by many unknown factors. Therefore, a general scalable framework of CRLB is required to further collect more information and evaluate the practical environment.
In this paper, we propose a general analysis method to evaluate the practical WSN localization system, which can fuse multiple pieces of information. The first major contribution is that we construct a scalable framework to model the multiple information fusion in the localization problem generally. We derive the Fisher information matrix (FIM) based on the proposed abstract function of all of the wireless localization system model instead of using a specific wireless propagation model. Furthermore, we employ an extendable estimated random vector , which contains all of the unknown parameters, e.g., the previous estimated state, the current state and the unknown indeterministic parameters that may influence the estimation accuracy. Then, we divide into two parts: the estimated state vector, which indicates the final position estimation, and the auxiliary vector, which helps improve the estimation accuracy. When only contains the state vectors or together with NLOS indicators, the our method is equivalent to the above-mentioned CRLBs. However, when a large number of parameters is involved in the estimation, e.g., the map information, the previous state, the relative height difference or the prior information of the unknown random parameters, our method can still provide practical optimal performance of the localization systems. The major advantage is that it is suitable for complicated and dynamic environment and fully considers the prior information, hybrid unknown factors and the recursive feature of the tracking algorithms.
The second contribution is that we employ the proposed CRLB framework to analyze the TOA range-based indoor localization system as a case study. The simulation environment considers all of the possible factors, e.g., the target-anchor geometry effect, the building layout, the relative height differences between the target and anchors, the NLOS transmission channel, the related prior information and the recursive feature of the tracking algorithm. The impact of each factor for the estimation accuracy is illustrated in the simulation. We use the spatial position error distribution (SPED) as a metric to evaluate the performance. The SPED indicates not only the target-anchor geometry effect, but also illustrates the impacts of height differences between the target and anchors, NLOS transmission and building layout information for the indoor localization. In addition, the impacts of the related prior information are also evaluated via SPED. To indicate which factor is important to the location estimation, we numerically evaluate the NLOS ranging, the height difference and the prior information in multiple scenarios. For the dynamic moving trajectories, the recursive form of the CRLB is applied. Finally, the estimation improvement using multiple anchors is also presented in the simulation. The results indicate that the NLOS ranging measurement mainly influences the estimation accuracy, and the prior information of the NLOS channel and the target position play important roles for improving the estimation. The relative height differences also degrade the estimation accuracy if we ignore them. However, with reliable prior information, we can make the estimation accuracy approach the location performance without any relative height differences. In general, our proposed method is suitable to exploit all of the available information to analyze the performance of the WSN localization system.
The rest parts of this paper is organized as follows:
Section 2 provides the WSN localization system model;
Section 3 introduces the scalable CRLB framework; then, we use the CRLB to derive the formulation of a practical TOA system in
Section 4; the simulation evaluations and analysis are illustrated in
Section 5; and
Section 6 concludes the whole paper. To make the content more clear, we list all of the fundamental notations in
Table 1 for the mathematical formulation.
5. Simulation
We set up several WSN localization simulations to evaluate the analytical performance. In each simulation, we consider several different factors, e.g., the recursive process during the target tracking, estimations with and without considering and . To make the results clear, we mark the CRLBs for different situations by adding superscripts and subscripts, which can be depicted as . The subscripts indicate the considered vectors, including the state vector and the auxiliary vector. This means that the system contains other factors in the ranging measurement, e.g., relative height or NLOS measurement or both. The superscripts indicate the available prior information of the related vectors. For instance, if we want to simulate the estimation with the NLOS range drift, the results of the CRLB are marked by . Additionally, if the prior information of is attained in the simulation, the results are marked by . For the recursive estimation, we use the notation to indicate the results, which considers the prior state . Note that, the superscript of in indicates that we have arbitrary prior knowledge of . This information is provided directly by the system instead of recursive estimation; while the superscript of in also means the prior knowledge of . However, such information is obtained based on the previous estimation of in the recursive target tracking. Thus, we use to analyze the static positioning scenarios and use to analyze the dynamic continuous target tracking scenarios. Some CRLB notations that appear in the following sections are listed below.
: Classical CRLB without any prior information, relative height or NLOS measurement
: CRLB when the relative height exists
: CRLB with the NLOS measurement
: CRLB both contains the relative height and NLOS measurement
: CRLB with the prior information of the relative height
: CRLB with the prior information of NLOS measurement
: CRLB with the arbitrary prior information of in the static scenario
: CRLB with the prior information based on in the dynamic scenario
To approach the real environment, we initially set the related parameters according to the test building in [
27]. Since the localization system can be affected by many factors, we tune the parameters to provide a comprehensive analysis in the following simulations, e.g.,
,
and the number of anchors. To better understand the performances in multiple environments, we uniformly locate the anchors in the SPED evaluation. Additionally, we evaluate the performances considering the relative height, NLOS and recursive estimation based on randomly-deployed anchors and Monte Carlo simulation to draw a general performance. In the real experiment, the anchors are randomly deployed throughout the whole building.
5.1. Spatial Position Error Distribution
In the first simulation, a
playing field with four anchors is constructed. All of the anchors are deployed on the roof being 2.5 m high, and the target is about 0.5∼1 m. To approach the real applications, we use several statistical results according to [
27]. We set the relative height as the constant value 1.5 m. The range error for each anchor follows zero-mean Gaussian distribution
, where
is the variance of
and is set to
. The range drift for the NLOS measurements is set to 2 m. For the prior information,
. The prior information of the NLOS range drift
is
. For the position state prior information, we assume that the prediction function is a linear static identity matrix with the zero-mean Gaussian prediction noise
, where
is the covariance of
. We assume
m.
We apply the CRLB to indicate the optimal squared error, which is
. To illustrate the target-anchor geometry effect for the 2D localization system in the playing field, we employ
to depict the spatial position error distribution (SPED) [
28]. The SPED is defined as the distribution of the position error for every possible target position, which estimates the positions point by point in the whole playing field and draws statistical results. Thus, every position in the playing field is assumed as the target position during the simulation. The SPED is derived according to all of the statistical results of the estimation error of all of the positions in the playing field. It illustrates how the performance changes according to the target-anchor (RX-TX) geometry effect. When the anchor positions and the error model change, the SPED changes accordingly, which helps to understand the relationship between the anchor deployment and the algorithm. The SPED results are represented by the contours in
Figure 2, where the four anchor positions are marked by triangles.
In
Figure 2a, the SPED is drawn based on the classical CRLB (
) in which the unknown vector is only
, and no relative height or NLOS propagation is introduced. When both
and
are introduced in the simulation, the dimension of the estimated vector is increased again. Then, a special pattern of the contours is drawn in
Figure 2b, which demonstrates that the estimation error is propagated and increased if more unknown factors are introduced. Each anchor seems to be a center of an independent contour area, and the estimation error is extremely larger than
Figure 2a, which indicates the strong uncertainty and a special geometric relationship between the target position and the anchor positions. Since more factors cannot be ignored in the complicated environment, the localization problem turns out to be a high dimensional estimation problem. It is quite possible that the squared error of the high dimensional estimation is larger than the low dimensional estimation, as the probability of the wrong estimation increases if more unknown parameters appear. Additionally, it also imposes new error on the original
estimation error. However, such a high dimensional localization problem cannot happen in the real world. On the one hand, the calculation complexity is increased dramatically in the real system, and only
is useful, which is a waste of computational resources. On the other hand, the algorithm designers ignore some unimportant factors, simplify the calculation and increase the estimation accuracy based on the prior knowledge.
Then, the prior information of
,
and
is used in the CRLB to improve the estimation accuracy. The SPEDs with prior information are depicted in
Figure 2c,d. When the prior state information of
is introduced in
Figure 2c, the estimation error is reduced effectively from more than 5 m in
Figure 2a to 1.4 m below. In addition, the position error is almost the same everywhere, although the geometric pattern is similar to
Figure 2a, which indicates that the geometric impact is reduced by using the prior information of
. In
Figure 2d, we assume that all of the prior information is available, then the estimation error is reduced to below 1.4 m, just as
Figure 2c. Although
Figure 2d still has a geometric pattern, which is similar to
Figure 2c, the errors in different positions are almost the same. Thus, the geometric effect is actually reduced. In addition, since the estimation error is not further reduced, the results in
Figure 2d can be the limits based on the prior information. It is also demonstrated that the prior information of
significantly reduces the estimation error and is the most important prior information especially in the recursive estimation. For the other two parts of the prior information, they are used for the improvement of the impacts of the relative height and the NLOS effects.
5.2. Impact of Relative Height
In this simulation, we evaluate the impact of the relative height independently. For the indoor localization, the relative height cannot be too high unless the room is tall enough. Thus, we choose the value of
between 0.5 m and 10 m. The simulation evaluates
and also
as a comparison. To illustrate the general relationship between the relative height and the measurement noise, we also tune the variance of the noise from
to
and
from 0.5 m and 10 m. In this simulation, we run 1000 Monte Carlo experiments. In each experiment, we choose a random position for analysis. The averaged results are listed in
Figure 3.
It is clearly observed that the estimation error rises according to the increase of
. However, the increased value is quite small. Take
Figure 3c for instance; the increased error is only 0.06 m when
is tuned from 0.5 m to 10 m, and the estimation error is 3.43 m by that time. Therefore, the value of
does not affect the estimation accuracy too much. On the other hand, the existence of
does affect the performance no matter what the value of
is. Compare the results in
Figure 3c;
affects the estimation with a typical certain value. When
is small, the average RMSE of
is 1.4390 m, but the average RMSE of
is 1.6856 m and
is 1.7137 m. According to the analytical results, when the relative height is introduced into the simulation, there is a gap between 2D localization without the relative height. Additionally, the gap becomes larger with the increased value of the measurement noise. Take
for instance; when
, the average RMSE is only 0.84 m. When
, the average RMSE without the relative height is about 8.3 m, which is almost 10-times that of the low noise. Thus, the relative height really affects the estimation no matter the value.
In addition, we evaluate the impact of the prior knowledge of
in the multiple noise environment. The simulation results are presented in
Figure 4. It is clearly observed that the prior knowledge can significantly improve the RMSE. If
, the prior information of
can even reduce 1 m RMSE. Additionally, if the error is small, the improvement is only a little bit. However, with the increased value of the relative height, the RMSE rises accordingly even with the prior information. For the real application, the relative height can be within 10 m, in which the improvement can effectively reduce the RMSE to a reasonable range. Therefore, even if the impact of the relative height is limited, it is still necessary to employ the prior information.
5.3. Impact of NLOS
The analysis of NLOS measurements has been mentioned in several literature works [
17,
18]. Here, we evaluate the impact of the number of NLOS measurements through simulations. The playing field is still
with 16 randomly-deployed anchors. We set up 1000 Monte Carlo runs, and a random set of anchors is chosen to have NLOS measurements. We tune the number of NLOS measurements from 1 to 16 and evaluate the performance of
and
. The averaged results are depicted in
Figure 5. It is observed that the RMSE of
increases according to the rise of the NLOS measurement number. It is also possible to have useless estimation when all of the measurements are NLOS, just as mentioned in [
17]. When there is only one NLOS measurement, the estimation error reaches 3 m. Additionally, the error is increased to 5 m if the number of NLOS measurements is changed to 16. In real applications, the number of NLOS measurements is unknown, and the system has to calculate all of the parameters from all of the measurements. Thus, the estimation error is quite high without the help of prior information. In addition, with the prior information of
, the estimation error is almost a constant value. Thus, the prior information of the NLOS measurement can successfully reduce the NLOS effect, which is applicable for real applications. Such prior information can be a combination of the building layout information and the wireless propagation model, e.g., map-matching-based algorithms [
13]. Additionally, several literature works have proposed many algorithms that either use pre-assumptions or estimate the parameters to obtain the NLOS information. The NLOS-related methods are beyond the scope of this paper; please refer to other research works in [
20,
23,
29].
5.4. Map Assist Localization System
In the following simulation, we evaluate a practical scenario where the layout of the building is involved. The playing field is still
. There are four big rooms located at four corners of the playing field. The area for each room is
. The rest of the playing field is the hallways. Four anchors are deployed inside each room and placed at the four corners. Thus, 16 anchors are uniformly deployed in the playing field, which is depicted in
Figure 6a. The triangles mark the positions of anchors. The LOS measurements can only be obtained in one room with four associate anchors, and others measurements are NLOS. For the positions in the hallways, all of the measurements are NLOS rangings.
All of the anchors are deployed on the roof with relative height 1∼2 m to the target. The distributions of the range error and the related prior information are the same in
Figure 2. The range drift for the NLOS measurements depends on the signal transmission from the anchor to the target. According to our previous research, the average positive NLOS drift of the signal through one wall is set to 2 m and to
for the signal through two or three walls if the signal can be detected [
30]. The prior information of the NLOS range drift
depends on the signal transmission. Here, we use the conclusions based on the experimental models in [
27]: the distribution for the signal transmission through one wall is
; the distribution for the signal transmission through more than two walls is
. In this simulation, we evaluate the SPED of
,
and
, which means that every position is calculated, and the error contours are drawn to indicate the target-anchor geometry effect. The results are depicted in
Figure 6.
For numerical comparison, the RMSE in
Figure 6b is higher than in
Figure 6c,d, which is more than 3.39 m in the central area. Additionally, the error becomes higher and higher when the position is approaching the corner, which is more than 8 m. Due to the lack of prior information, the geometric shape does not have special characteristics, which are related to rooms or corridors. The contours are almost like rectangles located in the center of the playing field. When the prior information of
and
is introduced, the accuracy is significantly improved, which is reduced to 2.55 m on average. The geometric shapes of the contours are different in the rooms and hallways. This indicates that the localization algorithms using the prior knowledge of NLOS conditions based on the building layout information and the NLOS identification and mitigation methods can reasonably improve the estimation performance. Thus, the layout information in the building map is an important information source for localizations. When the prior information of
is introduced in the estimation as indicated in
Figure 6d, the RMSE is further reduced, which is 1.235 m in almost all of the playing field where the target-anchor geometry effect is reduced effectively.
5.5. Bayesian-Based Target Tracking Estimation
In this simulation, we evaluate the performance of the recursive Bayesian estimation for target tracking. Since the impacts of
and
are extensively analyzed above, this section mainly focuses on analyzing the impact of
. The playing field is still
, and 16 anchors are deployed randomly in the field. We evaluate the CRLB in three scenarios: The first one considers NLOS and relative height measurement; the second scenario considers only the relative height; the third scenario only has NLOS measurement. In each scenario, both CRLB without prior information and the recursive CRLB with prior information based on (
27) are analyzed. Therefore, we evaluate
and
in the first scenario,
and
in the second scenario and
and
in the third scenario. We assume that the prior information is unknown initially in the recursive estimation. This information can only be obtained recursively after the initial estimation is obtained. Then, the recursive estimation is applied.
We run 1000 Monte Carlo simulations, and the target moves in a separate random path in each simulation. In addition, the target can also be static. Since
can also be estimated in the static scenario and be used for recursive estimation, the analysis results are the same as the dynamic target tracking scenarios. The estimation results are averaged and represented by the RMSE in
Figure 7. There are three solid parallel straight lines, which indicate the estimations without prior information:
,
and
. The three other dashed curves illustrate the recursive estimations according to time steps, which are
,
and
.
The Bayesian recursive estimation method with related prior information effectively reduced the estimation as indicated in
Figure 7. The RMSEs of the three curves gradually converge to low values according to time steps. The impacts of the relative heights and the NLOS drifts still degrade the estimation performance. Even with the recursive estimation, the estimation error cannot be further reduced, where the
is 0.5 m larger than
when
.
5.6. Multiple Anchors
The relationship between the CRLB and the number of anchors is illustrated in
Figure 8. We randomly deploy multiple anchors in the playing field. The number of anchors is adapted from four to 30. Both
and
are considered in this simulation. We assume that all of the measurements are NLOS. In this simulation, we evaluate
,
,
and
. With a few anchors,
contains large error, which achieves more than 15 m. When the number of anchors is four, the prior information of
and
can reduce much of the error as indicated by the curve of
. Furthermore, the recursive estimation based on
can reduce much of the error, which is even smaller than
. The error of the recursive estimation based on
is only a little lower than
. It is demonstrated that compared to the prior information of
and
,
is the dominant factor for reducing the estimation error. However, when the number of anchors is increased, all of the curves converge gradually to a low value. In this case, the prior information does not improve much for the estimation. Thus, even if the prior information is not available, using more observations still improves the estimation accuracy effectively.
5.7. Practical Evaluation
For practical usage, we employ the CRLB to evaluate a reference system. In this system, we deployed 17 wireless sensor nodes either along the corridor or in the offices of the research building. A robot carrying a sensor node as a target moved along the corridor of the building with constant speed while recording its own positions [
31]. All sensors are integrated with the nanoPAN 5375 RF (Nanotron Tech. GmbH, Berlin, Germany) module with a 2.4-GHz transceiver and a 1-Mbps data rate for range measurement, the LPC 2387 as the micro-controller (Nanotron Tech. GmbH, Berlin, Germany) and the CC1101 900-MHz transceiver (Nanotron Tech. GmbH, Berlin, Germany) as the radio transceiver for communication. The data collected from sensor nodes are also range measurement values, which are based on TOA.
Figure 9 depicts the map of our experimental building. The triangles, which are randomly deployed, mark the sensor node positions.
According to the collected data and map information, we construct the distribution model for both LOS and NLOS measurements, which are a zero-mean Gaussian distribution
;
is set to
for LOS measurement; and the NLOS measurements drift is set to 2 m. Then, the SPEDs with or without prior knowledge are depicted in
Figure 10. As illustrated in
Figure 10a, the overall estimation error can be extremely high due to the measurement error. In addition, the anchor-target geometry shape is seriously distorted due to the randomly-deployed anchor. In the corners of the building, the RMSEs are changing rapidly. However, with the help of prior information, we can effectively reduce the error to about 1.25 m.
5.8. Discussion
In this section, we use our proposed method to evaluate the optimal performance in multiple environments. It can be observed that our method can adapt the estimated parameters to fit the practical environment. In addition, the scalable architecture can effectively fuse multiple pieces of information, which outperforms other methods, which only consider parts of the information. In
Table 2, we compare our method to three mainly used CRLBs, which are generalized CRLB [
17], conditional CRLB [
16] and equivalent CRLB [
18]. The first row in
Table 2 indicates the considered information, and the word “prior” means the related prior information. As illustrated in the table, the generalized CRLB can only analyze the NLOS effect. The conditional CRLB provides the formulation of the state vector instead of other factors. The equivalent CRLB exploits more information. However, it is a closed form formulation, which is not scalable and cannot fuse the relative height information.
6. Conclusions
In this paper, we propose a scalable analyzing method for a WSN localization system, which can fuse multiple heterogeneous information to indicate the optimal performance. Theoretically, we divide the estimated vector into three parts: the estimated state vector and two auxiliary vectors. The recursive formulation of FIM is provided, which fully considers all of the possible factors that may influence the estimation accuracy, and it exploits all of the available information to derive the fundamental limits. It is a suitable tool to indicate the optimal estimation bound of practical systems.
We employ our theoretical contribution to analyze the TOA range-based WSN localization system. The impacts of the height and NLOS range drift are considered as the auxiliary vectors. The target-anchor geometry, prior information and the recursive form are extensively analyzed in the simulation. In addition, we employ a real test-bed and practical data to evaluate the overall performance. In the simulation, we find that both the relative height and NLOS impact can heavily degrade the estimation performance. However, many pieces of available information can improve it, e.g., the prior state distribution, the prior knowledge of the building and multiple anchors.
According to the simulation and experimental demonstration, the proposed CRLB is a general framework for analyzing the WSN localization systems, and it is not restricted to any specific technique. Future work will use the scalable CRLB to exploit other localization techniques and in other complicated environments to find potential factors that may influence the performance.