Novelty Detection using Deep Normative Modeling for IMU-Based Abnormal Movement Monitoring in Parkinson’s Disease and Autism Spectrum Disorders
Abstract
:1. Introduction
2. Related Works
3. Methods
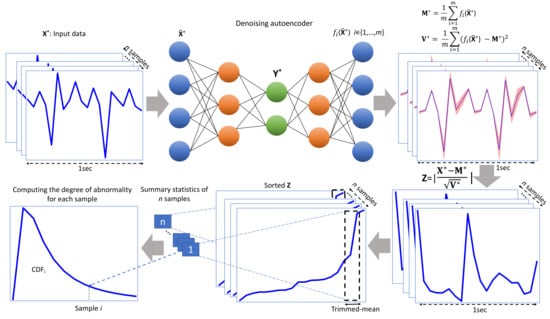
3.1. Learning the Distribution of Normal Movements via the Denoising Autoencoder
3.2. Quantifying the Deviation from
3.3. Computing the Degree of Novelty
3.4. Experimental Materials
3.4.1. Datasets
3.4.2. Network Architectures
- DAE architecture for the FOG dataset: The original CNN architecture in Hammerla et al. [8] was used for encoding the signal into a lower dimensional representation. This architecture contains four convolutional layers alternating convolution, batch normalization, Rectified Linear Units (ReLU) and max-pooling layers to map the large input space to a lower dimensional feature space. A fully-connected layer is then stacked on top of the fourth convolution layer to form the encoder. We concatenate a mirror reversal of the encoder network to the last encoder layer in order to reconstruct the input signal in a DAE architecture. In the decoding part, we replace max-pooling layers with up-sampling layers. In order to capture the model uncertainty, we placed a dropout layer before every weight layer [31]. The resulting architecture is shown in Figure 2a.
- DAE architecture for SMM datasets: Similar to [7], the encoder architecture consists of three convolutional layers, which alternates convolution, batch normalization, ReLUs and average-pooling layers to transform the raw feature space into a lower dimensional set of features. A fully-connected layer is then stacked on top of the third convolution layer. The resulting latent vector is then decoded in the decoder to reconstruct the input signal. Similar to the DAE architecture for the FOG dataset, the architecture of the decoder network is a mirror reversal of the encoder, and dropout layers are used before every weight layer. The architecture and the configuration of each layer are depicted in Figure 2b.
3.4.3. Experimental Setups and Evaluation
- Experiment 1, normative modeling: We followed the proposed procedure explained in Section 3, using the DAE architectures described in Section 3.4.2 for learning the distribution of the normal movements on the SMM-1, SMM-2 and FOG datasets. In this setting, models are trained in an unsupervised manner and only on the samples of normal movements. For training the DAEs, we used the RMSprop optimizer to minimize the mean squared error loss function. To compute and , we drew MC samples from DAE predictions, and the mean and variance across these 50 MC samples are used to compute the and matrices. In all experiments, we fix the dropout level to . Later in order to investigate the effect of the dropout level on the performance of the proposed novelty detection approach, we repeat this experiment for different dropout probability levels and compare the results.
- Experiment 2, reconstruction-based: The goal of this experiment is to assess the effect of incorporating prediction uncertainties, i.e., , on the performance of the novelty detection system. All the experimental settings in this experiment are similar to Experiment 1, except for computing the NPMs, where we use instead of Equation (2). Since in this setting, only the reconstruction error is used to construct a model of normal movements, we refer to this experiment as “reconstruction-based”.
- Experiment 3, one-class SVM: The goal in this experiment is to compare the proposed method for novelty detection with one-class classification. To this end, we train a one-class SVM model in a novelty detection setting [16,40,52,53]. One-class SVM fits a hyper-sphere decision boundary on a nonlinearly-transformed feature space to include the majority of samples in the normal class and detects anomalies as deviations from the learned decision boundary. In this experiment in a similar setting used by Erfani et al. [40], we use the learned reduced-rank latent space via the DAE model, i.e., , to train a one-class SVM model. We use this model later to distinguish the normal and abnormal movements on the samples. For the one-class SVM, we employed the implementation available in the scikit-learn [54] package. We used the Radial Basis Function (RBF) kernel with default hyperparameters, where and (Considering our assumption that only normal movement samples are available during the training phase, fine-tuning these hyperparameters is not possible. See Section 5.2 for the discussion.).
4. Results
4.1. Normative Modeling Outperforms Reconstruction-Based and One-Class SVM in Novelty Detection
4.2. Novelty Detection Methods vs. Supervised Learning Methods
4.3. Effect of Dropout Level
4.4. Training Only on Normal Subjects
5. Discussion
5.1. Estimating the Prediction Uncertainty: Deep Learning vs. Gaussian Processes
5.2. Normative Modeling vs. One-Class Classification
5.3. Toward Modeling Human Normal Daily Movements Using Wearable Sensors
5.4. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IMU | Inertial Measurement Unit |
| PD | Parkinson’s Disease |
| ASD | Autism Spectrum Disorder |
| FOG | Freezing Of Gait |
| SMM | Stereotypical Motor Movements |
| DAE | Denoising Autoencoder |
| GEVD | Generalized Extreme Value Distribution |
| CNN | Convolutional Neural Network |
| ReLU | Rectified Linear Units |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
| ROC | Receiver Operating Characteristic |
| AUC | Area Under the Curve |
| AUPR | Area Under the Precision-Recall Curve |
| MC | Monte Carlo |
| MTGPR | Multi-Task Gaussian Process Regression |
Appendix A. Generalized Extreme Value Distribution
References
- Gelb, D.J.; Oliver, E.; Gilman, S. Diagnostic criteria for Parkinson disease. Arch. Neurol. 1999, 56, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Lord, C.; Cook, E.H.; Leventhal, B.L.; Amaral, D.G. Autism spectrum disorders. Neuron 2000, 28, 355–363. [Google Scholar] [CrossRef]
- Goodwin, M.S.; Haghighi, M.; Tang, Q.; Akcakaya, M.; Erdogmus, D.; Intille, S. Moving towards a real-time system for automatically recognizing stereotypical motor movements in individuals on the autism spectrum using wireless accelerometry. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 861–872. [Google Scholar]
- Tao, W.; Liu, T.; Zheng, R.; Feng, H. Gait analysis using wearable sensors. Sensors 2012, 12, 2255–2283. [Google Scholar] [CrossRef] [PubMed]
- Uitti, R.J.; Baba, Y.; Wszolek, Z.K.; Putzke, D.J. Defining the Parkinson’s disease phenotype: Initial symptoms and baseline characteristics in a clinical cohort. Parkinsonism Relat. Disord. 2005, 11, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Morgan, L.; Wetherby, A.M.; Barber, A. Repetitive and stereotyped movements in children with autism spectrum disorders late in the second year of life. J. Child Psychol. Psychiatry 2009, 49, 826–837. [Google Scholar] [CrossRef] [PubMed]
- Rad, N.M.; Kia, S.M.; Zarbo, C.; van Laarhoven, T.; Jurman, G.; Venuti, P.; Marchiori, E.; Furlanello, C. Deep learning for automatic stereotypical motor movement detection using wearable sensors in autism spectrum disorders. Signal Process. 2018, 144, 180–191. [Google Scholar] [Green Version]
- Hammerla, N.Y.; Halloran, S.; Ploetz, T. Deep, convolutional, and recurrent models for human activity recognition using wearables. arXiv, 2016; arXiv:1604.08880. [Google Scholar]
- Camps, J.; Sama, A.; Martin, M.; Rodriguez-Martin, D.; Perez-Lopez, C.; Arostegui, J.M.M.; Cabestany, J.; Catala, A.; Alcaine, S.; Mestre, B.; et al. Deep learning for freezing of gait detection in Parkinson’s disease patients in their homes using a waist-worn inertial measurement unit. Knowl.-Based Syst. 2018, 139, 119–131. [Google Scholar] [CrossRef]
- Trabelsi, D.; Mohammed, S.; Chamroukhi, F.; Oukhellou, L.; Amirat, Y. An unsupervised approach for automatic activity recognition based on hidden Markov model regression. IEEE Trans. Autom. Sci. Eng. 2013, 10, 829–835. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 15. [Google Scholar] [CrossRef]
- Scott, C.; Blanchard, G. Novelty detection: Unlabeled data definitely help. In Proceedings of the Twelth International Conference on Artificial Intelligence and Statistics, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 464–471. [Google Scholar]
- Rad, N.M.; Kia, S.M.; Zarbo, C.; Jurman, G.; Venuti, P.; Furlanello, C. Stereotypical motor movement detection in dynamic feature space. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 487–494. [Google Scholar]
- Mazilu, S.; Blanke, U.; Calatroni, A.; Gazit, E.; Hausdorff, J.M.; Tröster, G. The role of wrist-mounted inertial sensors in detecting gait freeze episodes in Parkinson’s disease. Pervasive Mob. Comput. 2016, 33, 1–16. [Google Scholar] [CrossRef]
- Marquand, A.F.; Wolfers, T.; Mennes, M.; Buitelaar, J.; Beckmann, C.F. Beyond lumping and splitting: A review of computational approaches for stratifying psychiatric disorders. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2016, 1, 433–447. [Google Scholar] [CrossRef] [PubMed]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Jyothsna, V.; Prasad, V.R.; Prasad, K.M. A review of anomaly based intrusion detection systems. Int. J. Comput. Appl. 2011, 28, 26–35. [Google Scholar] [CrossRef]
- Jose, S.; Malathi, D.; Reddy, B.; Jayaseeli, D. A Survey on Anomaly Based Host Intrusion Detection System. J. Phys. Conf. Ser. 2018, 1000, 012049. [Google Scholar] [CrossRef]
- Tarassenko, L.; Hayton, P.; Cerneaz, N.; Brady, M. Novelty detection for the identification of masses in mammograms. In Proceedings of the 4th International Conference on Artificial Neural Networks, Cambridge, UK, 26–28 June 1995. [Google Scholar]
- Quinn, J.A.; Williams, C.K. Known unknowns: Novelty detection in condition monitoring. In Proceedings of the 2007 Iberian Conference on Pattern Recognition and Image Analysis, Girona, Spain, 6–8 June 2007; pp. 1–6. [Google Scholar]
- Kia, S.M.; Backmann, C.F.; Marquand, A.F. Scalable Multi-Task Gaussian Process Tensor Regression for Normative Modeling of Structured Variation in Neuroimaging Data. arXiv, 2018; arXiv:1808.00036. [Google Scholar]
- Zhang, Y.; Bingham, C.; Martínez-García, M.; Cox, D. Detection of emerging faults on industrial gas turbines using extended Gaussian mixture models. Int. J. Rotating Mach. 2017, 2017. [Google Scholar] [CrossRef]
- Słoński, M. Gaussian mixture model for time series-based structural damage detection. Comput. Assist. Methods Eng. Sci. 2017, 19, 331–338. [Google Scholar]
- Chen, L.J.; Ho, Y.H.; Hsieh, H.H.; Huang, S.T.; Lee, H.C.; Mahajan, S. ADF: an Anomaly Detection Framework for Large-scale PM2. 5 Sensing Systems. IEEE Internet Things J. 2018, 5, 559–570. [Google Scholar] [CrossRef]
- Islam, R.U.; Hossain, M.S.; Andersson, K. A novel anomaly detection algorithm for sensor data under uncertainty. Soft Comput. 2018, 22, 1623–1639. [Google Scholar] [CrossRef]
- Sabokrou, M.; Fayyaz, M.; Fathy, M.; Moayed, Z.; Klette, R. Deep-anomaly: Fully convolutional neural network for fast anomaly detection in crowded scenes. Comput. Vis. Image Understand. 2018. [Google Scholar] [CrossRef]
- Sultani, W.; Chen, C.; Shah, M. Real-world Anomaly Detection in Surveillance Videos. arXiv, 2018; arXiv:1801.04264. [Google Scholar]
- Khreich, W.; Khosravifar, B.; Hamou-Lhadj, A.; Talhi, C. An anomaly detection system based on variable N-gram features and one-class SVM. Inf. Softw. Technol. 2017, 91, 186–197. [Google Scholar] [CrossRef]
- Vaarandi, R.; Blumbergs, B.; Kont, M. An unsupervised framework for detecting anomalous messages from syslog log files. In Proceedings of the NOMS 2018 IEEE/IFIP Network Operations and Management Symposium, Taipei, Taiwan, 23–27 April 2018. [Google Scholar]
- Marquand, A.F.; Rezek, I.; Buitelaar, J.; Beckmann, C.F. Understanding heterogeneity in clinical cohorts using normative models: Beyond case-control studies. Biol. Psychiatry 2016, 80, 552–561. [Google Scholar] [CrossRef] [PubMed]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the 2016 International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Tripoliti, E.E.; Tzallas, A.T.; Tsipouras, M.G.; Rigas, G.; Bougia, P.; Leontiou, M.; Konitsiotis, S.; Chondrogiorgi, M.; Tsouli, S.; Fotiadis, D.I. Automatic detection of freezing of gait events in patients with Parkinson’s disease. Comput. Methods Programs Biomed. 2013, 110, 12–26. [Google Scholar] [CrossRef] [PubMed]
- Mazilu, S.; Hardegger, M.; Zhu, Z.; Roggen, D.; Troster, G.; Plotnik, M.; Hausdorff, J.M. Online detection of freezing of gait with smartphones and machine learning techniques. In Proceedings of the 2012 6th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth), San Diego, CA, USA, 21–24 May 2012; pp. 123–130. [Google Scholar]
- Rodríguez-Martín, D.; Samà, A.; Pérez-López, C.; Català, A.; Arostegui, J.M.M.; Cabestany, J.; Bayés, À.; Alcaine, S.; Mestre, B.; Prats, A.; et al. Home detection of freezing of gait using support vector machines through a single waist-worn triaxial accelerometer. PLoS ONE 2017, 12, e0171764. [Google Scholar] [CrossRef] [PubMed]
- Rad, N.M.; Bizzego, A.; Kia, S.M.; Jurman, G.; Venuti, P.; Furlanello, C. Convolutional neural network for stereotypical motor movement detection in autism. arXiv, 2015; arXiv:1511.01865. [Google Scholar]
- Großekathöfer, U.; Manyakov, N.V.; Mihajlović, V.; Pandina, G.; Skalkin, A.; Ness, S.; Bangerter, A.; Goodwin, M.S. Automated detection of stereotypical motor movements in autism spectrum disorder using recurrence quantification analysis. Front. Neuroinform. 2017, 11, 9. [Google Scholar] [CrossRef] [PubMed]
- Rad, N.M.; Furlanello, C. Applying deep learning to stereotypical motor movement detection in autism spectrum disorders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 1235–1242. [Google Scholar]
- Cola, G.; Avvenuti, M.; Vecchio, A.; Yang, G.Z.; Lo, B. An on-node processing approach for anomaly detection in gait. IEEE Sens. J. 2015, 15, 6640–6649. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Huynh, H.H.; Meunier, J. Skeleton-based abnormal gait detection. Sensors 2016, 16, 1792. [Google Scholar] [CrossRef] [PubMed]
- Erfani, S.M.; Rajasegarar, S.; Karunasekera, S.; Leckie, C. High-dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning. Pattern Recognit. 2016, 58, 121–134. [Google Scholar] [CrossRef]
- Vasilev, A.; Golkov, V.; Lipp, I.; Sgarlata, E.; Tomassini, V.; Jones, D.K.; Cremers, D. q-Space Novelty Detection with Variational Autoencoders. arXiv, 2018; arXiv:1806.02997. [Google Scholar]
- Chen, X.; Pawlowski, N.; Rajchl, M.; Glocker, B.; Konukoglu, E. Deep Generative Models in the Real-World: An Open Challenge from Medical Imaging. arXiv, 2018; arXiv:1806.05452. [Google Scholar]
- Khan, S.S.; Taati, B. Detecting unseen falls from wearable devices using channel-wise ensemble of autoencoders. Expert Syst. Appl. 2017, 87, 280–290. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, G.; Ridgway, G.R.; Dahnke, R.; Gaser, C.; Alzheimer’s Disease Neuroimaging Initiative. Individualized Gaussian process-based prediction and detection of local and global gray matter abnormalities in elderly subjects. NeuroImage 2014, 97, 333–348. [Google Scholar] [CrossRef] [PubMed]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Davison, A.C.; Huser, R. Statistics of extremes. Annu. Rev. Stat. Appl. 2015, 2, 203–235. [Google Scholar] [CrossRef]
- Roberts, S.J. Extreme value statistics for novelty detection in biomedical data processing. IEE Proc.-Sci. Meas. Technol. 2000, 147, 363–367. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.C.; Smola, A.J.; Williamson, R.C. Estimating the Support of a High-Dimensional Distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bachlin, M.; Roggen, D.; Troster, G.; Plotnik, M.; Inbar, N.; Meidan, I.; Herman, T.; Brozgol, M.; Shaviv, E.; Giladi, N.; et al. Potentials of enhanced context awareness in wearable assistants for Parkinson’s disease patients with the freezing of gait syndrome. In Proceedings of the ISWC’09 International Symposium on Wearable Computers, Linz, Austria, 4–7 September 2009; pp. 123–130. [Google Scholar]
- Lam, K.S.; Aman, M.G. The Repetitive Behavior Scale-Revised: Independent validation in individuals with autism spectrum disorders. J. Autism Dev. Disord. 2007, 37, 855–866. [Google Scholar] [CrossRef] [PubMed]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 18 September 2018).
- Rajasegarar, S.; Leckie, C.; Bezdek, J.C.; Palaniswami, M. Centered hyperspherical and hyperellipsoidal one-class support vector machines for anomaly detection in sensor networks. IEEE Trans. Inf. Forensics Secur. 2010, 5, 518–533. [Google Scholar] [CrossRef]
- Clifton, L.A.; Yin, H.; Zhang, Y. Support vector machine in novelty detection for multi-channel combustion data. In International Symposium on Neural Networks; Springer: Berlin/Heidelberg, Germany, 2006; pp. 836–843. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Albinali, F.; Goodwin, M.S.; Intille, S.S. Recognizing stereotypical motor movements in the laboratory and classroom: A case study with children on the autism spectrum. In Proceedings of the 11th International Conference on Ubiquitous Computing, Orlando, FL, USA, 30 September–3 October 2009; pp. 71–80. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Bonilla, E.V.; Chai, K.M.; Williams, C. Multi-task Gaussian process prediction. In Proceedings of the Neural Information Processing Systems 2008, Vancouver, BC, Canada, 8–10 December 2008; pp. 153–160. [Google Scholar]
- Álvarez, M.A.; Lawrence, N.D. Computationally efficient convolved multiple output Gaussian processes. J. Mach. Learn. Res. 2011, 12, 1459–1500. [Google Scholar]
- Rakitsch, B.; Lippert, C.; Borgwardt, K.; Stegle, O. It is all in the noise: Efficient multi-task Gaussian process inference with structured residuals. In Proceedings of the Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1466–1474. [Google Scholar]
- Kia, S.M.; Marquand, A. Normative Modeling of Neuroimaging Data using Scalable Multi-Task Gaussian Processes. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018. [Google Scholar]
- Moya, M.M.; Koch, M.W.; Hostetler, L.D. One-class classifier networks for target recognition applications. In NASA STI/Recon Technical Report N; NASA: Washington, DC, USA, 1993; Volume 93. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv, 2013; arXiv:1312.6114. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv, 2015; arXiv:1511.05644. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]




| Data | Subject | #Normal | #Abnormal | All | Abnormal/All | Gender |
|---|---|---|---|---|---|---|
| FOG | Sub1 | 5714 | 334 | 6048 | M | |
| Sub2 | 3918 | 578 | 4496 | M | ||
| Sub3 | 5488 | 912 | 6400 | M | ||
| Sub4 | 6592 | 0 | 6592 | 0 | M | |
| Sub5 | 5139 | 1517 | 6656 | M | ||
| Sub6 | 5917 | 419 | 6336 | F | ||
| Sub7 | 4858 | 262 | 5120 | M | ||
| Sub8 | 1812 | 620 | 2432 | F | ||
| Sub9 | 4673 | 863 | 5536 | M | ||
| Sub10 | 7104 | 0 | 7104 | 0 | F | |
| Total | 50,482 | 6238 | 56,720 | - | ||
| SMM-1 | Sub1 | 21,292 | 5663 | 26,955 | M | |
| Sub2 | 12,763 | 4372 | 17,135 | M | ||
| Sub3 | 31,780 | 2855 | 34,635 | M | ||
| Sub4 | 10,571 | 10,243 | 20,814 | 0.49 | M | |
| Sub5 | 17,782 | 6173 | 23,955 | 0.26 | M | |
| Sub6 | 12,207 | 17,725 | 29,932 | 0.59 | M | |
| Total | 106,395 | 47,031 | 153,426 | 0.31 | - | |
| SMM-2 | Sub1 | 18,729 | 11,656 | 30,385 | 0.38 | M |
| Sub2 | 22,611 | 4804 | 27,415 | 0.18 | M | |
| Sub3 | 40,557 | 268 | 40,825 | 0.01 | M | |
| Sub4 | 38,796 | 8176 | 46,972 | 0.17 | M | |
| Sub5 | 22,896 | 6728 | 29,624 | 0.23 | M | |
| Sub6 | 2375 | 11,178 | 13,553 | 0.82 | M | |
| Total | 145,964 | 42,810 | 188,774 | 0.23 | - |
| Dataset | Subject | Normative | Reconstruction | 1C-SVM | Supervised |
|---|---|---|---|---|---|
| FOG | Sub1 | ||||
| Sub2 | |||||
| Sub3 | |||||
| Sub5 | |||||
| Sub6 | |||||
| Sub7 | |||||
| Sub8 | |||||
| Sub9 | |||||
| Mean | ± | ||||
| SMM-1 | Sub1 | ||||
| Sub2 | |||||
| Sub3 | |||||
| Sub4 | |||||
| Sub5 | |||||
| Sub6 | |||||
| Mean | ± | ||||
| SMM-2 | Sub1 | ||||
| Sub2 | |||||
| Sub3 | |||||
| Sub4 | |||||
| Sub5 | |||||
| Sub6 | |||||
| Mean | ± |
| Dataset | Subject | Normative | Reconstruction | 1C-SVM | Supervised |
|---|---|---|---|---|---|
| FOG | Sub1 | ||||
| Sub2 | |||||
| Sub3 | |||||
| Sub5 | |||||
| Sub6 | |||||
| Sub7 | |||||
| Sub8 | |||||
| Sub9 | |||||
| Mean | ± | ||||
| SMM-1 | Sub1 | ||||
| Sub2 | |||||
| Sub3 | |||||
| Sub4 | |||||
| Sub5 | |||||
| Sub6 | |||||
| Mean | ± | ||||
| SMM-2 | Sub1 | ||||
| Sub2 | |||||
| Sub3 | |||||
| Sub4 | |||||
| Sub5 | |||||
| Sub6 | |||||
| Mean | ± |
| Dataset | Subject | Normative | Reconstruction | 1C-SVM |
|---|---|---|---|---|
| FOG | Sub1 | |||
| Sub2 | ||||
| Sub3 | ||||
| Sub5 | ||||
| Sub6 | ||||
| Sub7 | ||||
| Sub8 | ||||
| Sub9 | ||||
| Mean | ± |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadian Rad, N.; Van Laarhoven, T.; Furlanello, C.; Marchiori, E. Novelty Detection using Deep Normative Modeling for IMU-Based Abnormal Movement Monitoring in Parkinson’s Disease and Autism Spectrum Disorders. Sensors 2018, 18, 3533. https://doi.org/10.3390/s18103533
Mohammadian Rad N, Van Laarhoven T, Furlanello C, Marchiori E. Novelty Detection using Deep Normative Modeling for IMU-Based Abnormal Movement Monitoring in Parkinson’s Disease and Autism Spectrum Disorders. Sensors. 2018; 18(10):3533. https://doi.org/10.3390/s18103533
Chicago/Turabian StyleMohammadian Rad, Nastaran, Twan Van Laarhoven, Cesare Furlanello, and Elena Marchiori. 2018. "Novelty Detection using Deep Normative Modeling for IMU-Based Abnormal Movement Monitoring in Parkinson’s Disease and Autism Spectrum Disorders" Sensors 18, no. 10: 3533. https://doi.org/10.3390/s18103533
APA StyleMohammadian Rad, N., Van Laarhoven, T., Furlanello, C., & Marchiori, E. (2018). Novelty Detection using Deep Normative Modeling for IMU-Based Abnormal Movement Monitoring in Parkinson’s Disease and Autism Spectrum Disorders. Sensors, 18(10), 3533. https://doi.org/10.3390/s18103533