Design and Implementation of a Stereo Vision System on an Innovative 6DOF Single-Edge Machining Device for Tool Tip Localization and Path Correction †
Abstract
:1. Introduction
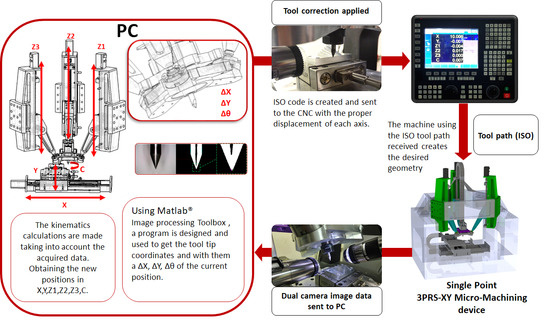
2. Description of the 6DOF Single-Edge Machining Device
Inverse Kinematics of the 6DOF Machine Tool
3. Stereo Vision System
3.1. Materials
3.2. Schema of the Stereo Vision System
3.2.1. Image Acquisition
3.2.2. Tool Localization
3.2.3. Alignment of the Tool with Respect to the Cameras
3.2.4. Tool Tip Localization
3.2.5. Path Correction
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. ISO Programs for the Cutting Paths of Figure 17
Appendix A.1.1. ISO Program without Tool Tip Correction
| V.A.ORGT[2].X = −71.676 |
| V.A.ORGT[2].Y = 21.309 |
| V.A.ORGT[2].Z1 = −140.630 |
| V.A.ORGT[2].Z2 = −140.630 |
| V.A.ORGT[2].Z3 = −140.630 |
| V.A.ORGT[2].C = 80 |
| G55 |
| P1 = 0 |
| G01 X0 Y0 Z1 = 0 Z2 = 0 Z3 = 0 C0 F100 (PRIORITY 1 BEGIN) |
| $WHILE P1 ≤ 44 |
| P1 = P1 + 11 |
| G17 G71 G94 |
| G02 X3 Y3 I3 J0 C90 |
| G02 X6 Y0 I0 J3 C180 |
| G03 X8.5 Y-3 I-3 J0 C90 |
| G03 X11 Y0 I0 J-2 C180 |
| G158 XP1 |
| $ENDWHILE |
| G01 Z1 = 1 Z2 = 1 Z3 = 1 F50 |
| G01 X-55 F500 |
| G54 |
| G158 |
| M3 |
Appendix A.1.2. ISO Program with Tool Tip Correction
| V.A.ORGT[2].X = −71.676 | N220 G01 X-0.300 Y-1.027 C21.0 | N3320 G01 X10.378 Y1.330 C29.0 |
| N230 G01 X-0.305 Y-1.078 C22.0 | N3330 G01 X10.424 Y1.294 C28.0 | |
| V.A.ORGT[2].Y = 21.309 | N240 G01 X-0.309 Y-1.129 C23.0 | N3340 G01 X10.470 Y1.257 C27.0 |
| V.A.ORGT[2].Z1 = −140.630 | N250 G01 X-0.312 Y-1.180 C24.0 | N3350 G01 X10.514 Y1.219 C26.0 |
| V.A.ORGT[2].Z2 = −140.630 | N260 G01 X-0.314 Y-1.232 C25.0 | N3360 G01 X10.558 Y1.181 C25.0 |
| V.A.ORGT[2].Z3 = −140.630 | N270 G01 X-0.315 Y-1.283 C26.0 | N3370 G01 X10.602 Y1.141 C24.0 |
| V.A.ORGT[2].C = 80 | N280 G01 X-0.315 Y-1.334 C27.0 | N3380 G01 X10.644 Y1.101 C23.0 |
| N290 G01 X-0.315 Y-1.385 C28.0 | N3390 G01 X10.686 Y1.060 C22.0 | |
| G55 | N300 G01 X-0.313 Y-1.436 C29.0 | N3400 G01 X10.728 Y1.019 C21.0 |
| P1 = 0 | N310 G01 X-0.311 Y-1.488 C30.0 | N3410 G01 X10.768 Y0.976 C20.0 |
| N320 G01 X-0.308 Y-1.539 C31.0 | N3420 G01 X10.808 Y0.933 C19.0 | |
| G01 X0 Y0 Z1 = 0 Z2 = 0 Z3 = 0 C0 F100 (PRIORITY 1 BEGIN) | N330 G01 X-0.303 Y-1.590 C32.0 | N3430 G01 X10.847 Y0.890 C18.0 |
| N340 G01 X-0.298 Y-1.641 C33.0 | N3440 G01 X10.885 Y0.845 C17.0 | |
| N350 G01 X-0.292 Y-1.692 C34.0 | N3450 G01 X10.923 Y0.800 C16.0 | |
| $WHILE P1 <= 44 | N360 G01 X-0.285 Y-1.743 C35.0 | N3460 G01 X10.959 Y0.755 C15.0 |
| N370 G01 X-0.278 Y-1.793 C36.0 | N3470 G01 X10.995 Y0.708 C14.0 | |
| P1 = P1 + 11 | N380 G01 X-0.269 Y-1.844 C37.0 | N3480 G01 X11.030 Y0.661 C13.0 |
| N390 G01 X-0.260 Y-1.894 C38.0 | N3490 G01 X11.064 Y0.614 C12.0 | |
| G17 G71 G94 | N400 G01 X-0.249 Y-1.944 C39.0 | N3500 G01 X11.098 Y0.566 C11.0 |
| N410 G01 X-0.238 Y-1.994 C40.0 | N3510 G01 X11.130 Y0.517 C10.0 | |
| N10 G01 X-0.000 Y0.000 C0.000 F1000 | N420 G01 X-0.226 Y-2.044 C41.0 | N3520 G01 X11.162 Y0.468 C9.00 |
| N20 G01 X-0.023 Y-0.046 C1.000 | N430 G01 X-0.213 Y-2.094 C42.0 | N3530 G01 X11.193 Y0.418 C8.00 |
| N30 G01 X-0.045 Y-0.092 C2.000 | N440 G01 X-0.199 Y-2.143 C43.0 | N3540 G01 X11.223 Y0.368 C7.00 |
| N40 G01 X-0.066 Y-0.139 C3.000 | N450 G01 X-0.184 Y-2.192 C44.0 | N3550 G01 X11.252 Y0.317 C6.00 |
| N50 G01 X-0.086 Y-0.186 C4.000 | N460 G01 X-0.169 Y-2.241 C45.0 | N3560 G01 X11.280 Y0.265 C5.00 |
| N60 G01 X-0.105 Y-0.233 C5.000 | N470 G01 X-0.152 Y-2.289 C46.0 | N3570 G01 X11.307 Y0.214 C4.00 |
| N70 G01 X-0.124 Y-0.281 C6.000 | N480 G01 X-0.135 Y-2.338 C47.0 | N3580 G01 X11.334 Y0.161 C3.00 |
| N80 G01 X-0.142 Y-0.329 C7.000 | N490 G01 X-0.117 Y-2.386 C48.0 | N3590 G01 X11.359 Y0.109 C2.00 |
| N90 G01 X-0.159 Y-0.378 C8.000 | N500 G01 X-0.098 Y-2.433 C49.0 | N3600 G01 X11.384 Y0.055 C1.00 |
| N100 G01 X-0.175 Y-0.426 C9.00 | N510 G01 X-0.078 Y-2.480 C50.0 | N3610 G01 X11.407 Y0.002 C0.00 |
| N110 G01 X-0.190 Y-0.475 C10.0 |  | G158 XP1 |
| N120 G01 X-0.204 Y-0.524 C11.0 | $ENDWHILE | |
| N130 G01 X-0.218 Y-0.574 C12.0 | G01 Z1 = 1 Z2 = 1 Z3 = 1 F50 | |
| N140 G01 X-0.231 Y-0.623 C13.0 | G01 X-48 F500 | |
| N150 G01 X-0.242 Y-0.673 C14.0 | ||
| N160 G01 X-0.253 Y-0.723 C15.0 | G54 | |
| N170 G01 X-0.263 Y-0.774 C16.0 | G158 | |
| N180 G01 X-0.273 Y-0.824 C17.0 | ||
| N190 G01 X-0.281 Y-0.875 C18.0 | N3290 G01 X10.237 Y1.434 C32.0 | M30 |
| N200 G01 X-0.288 Y-0.925 C19.0 | N3300 G01 X10.285 Y1.400 C31.0 | |
| N210 G01 X-0.295 Y-0.976 C20.0 | N3310 G01 X10.332 Y1.366 C30.0 |
Appendix A.2. ISO Programs for the Cutting Paths of Figure 18
Appendix A.2.1. ISO Program without Tool Tip Correction
| V.A.ORGT[2].X = −51 |
| V.A.ORGT[2].Y = 33 |
| V.A.ORGT[2].Z1 = −140.630 |
| V.A.ORGT[2].Z2 = −140.630 |
| V.A.ORGT[2].Z3 = −140.630 |
| V.A.ORGT[2].C = 80 |
| G55 |
| G01 X0 Y0 Z1 = 0 Z2 = 0 Z3 = 0 C0 F100 (PRIORITY 1 BEGIN) |
| G17 G71 G94 |
| G02 X0.5 Y0.5 I0.5 J0 C90 |
| G02 X1 Y0 I0 J0.5 C180 |
| G02 X0.5 Y-0.5 I-0.5 J0 C270 |
| G02 X0 Y0 I0 J-0.5 C360 |
| G01 Z1 = 1 Z2 = 1 Z3 = 1 F50 |
| G01 X0 F500 |
| G54 |
| G158 |
| M30 |
Appendix A.2.2. ISO Program without Tool Tip Correction
| V.A.ORGT[2].X = −53 | N310 G01 X-0.387 Y-0.539 C30.0 | N3270 G01 X0.693 Y0.285 C326.0 |
| V.A.ORGT[2].Y = 33 | N320 G01 X-0.394 Y-0.560 C31.0 | N3280 G01 X0.671 Y0.283 C327.0 |
| V.A.ORGT[2].Z1 = −140.630 | N330 G01 X-0.402 Y-0.581 C32.0 | N3290 G01 X0.649 Y0.280 C328.0 |
| V.A.ORGT[2].Z2 = −140.630 | N340 G01 X-0.409 Y-0.603 C33.0 | N3200 G01 X0.627 Y0.277 C329.0 |
| V.A.ORGT[2].Z3 = −140.630 | N350 G01 X-0.415 Y-0.624 C34.0 | N3310 G01 X0.604 Y0.274 C330.0 |
| V.A.ORGT[2].C = 80 | N360 G01 X-0.421 Y-0.646 C35.0 | N3320 G01 X0.582 Y0.270 C331.0 |
| N370 G01 X-0.427 Y-0.667 C36.0 | N3330 G01 X0.560 Y0.266 C332.0 | |
| G55 | N380 G01 X-0.433 Y-0.689 C37.0 | N3340 G01 X0.539 Y0.261 C333.0 |
| N390 G01 X-0.438 Y-0.711 C38.0 | N3350 G01 X0.517 Y0.256 C334.0 | |
| G01 X0 Y0 Z1 = 0 Z2 = 0 Z3 = 0 C0 F100 (PRIORITY 1 BEGIN) | N400 G01 X-0.443 Y-0.733 C39.0 | N3360 G01 X0.495 Y0.251 C335.0 |
| N410 G01 X-0.447 Y-0.754 C40.0 | N3370 G01 X0.473 Y0.245 C336.0 | |
| N420 G01 X-0.451 Y-0.776 C41.0 | N3380 G01 X0.452 Y0.239 C337.0 | |
| N10 G01 X0.000 Y0.000 C0.000 | N430 G01 X-0.454 Y-0.799 C42.0 | N3390 G01 X0.430 Y0.232 C338.0 |
| N20 G01 X-0.017 Y-0.014 C1.000 | N440 G01 X-0.458 Y-0.821 C43.0 | N3400 G01 X0.409 Y0.226 C339.0 |
| N30 G01 X-0.034 Y-0.029 C2.000 | N450 G01 X-0.460 Y-0.843 C44.0 | N3410 G01 X0.388 Y0.218 C340.0 |
| N40 G01 X-0.051 Y-0.044 C3.000 | N460 G01 X-0.463 Y-0.865 C45.0 | N3420 G01 X0.367 Y0.211 C341.0 |
| N50 G01 X-0.067 Y-0.059 C4.000 | N470 G01 X-0.465 Y-0.887 C46.0 | N3430 G01 X0.346 Y0.203 C342.0 |
| N60 G01 X-0.083 Y-0.075 C5.000 | N480 G01 X-0.466 Y-0.910 C47.0 | N3440 G01 X0.325 Y0.194 C343.0 |
| N70 G01 X-0.099 Y-0.090 C6.000 | N490 G01 X-0.468 Y-0.932 C48.0 | N3450 G01 X0.305 Y0.186 C344.0 |
| N80 G01 X-0.115 Y-0.106 C7.000 | N500 G01 X-0.468 Y-0.954 C49.0 | N3460 G01 X0.284 Y0.177 C345.0 |
| N90 G01 X-0.130 Y-0.123 C8.000 | N510 G01 X-0.469 Y-0.977 C50.0 | N3470 G01 X0.264 Y0.167 C346.0 |
| N100 G01 X-0.145 Y-0.139 C9.00 | N520 G01 X-0.469 Y-0.999 C51.0 | N3480 G01 X0.244 Y0.157 C347.0 |
| N110 G01 X-0.160 Y-0.156 C10.0 | N530 G01 X-0.469 Y-1.022 C52.0 | N3490 G01 X0.224 Y0.147 C348.0 |
| N120 G01 X-0.174 Y-0.173 C11.0 | N540 G01 X-0.468 Y-1.044 C53.0 | N3500 G01 X0.204 Y0.137 C349.0 |
| N130 G01 X-0.188 Y-0.191 C12.0 | N550 G01 X-0.467 Y-1.066 C54.0 | N3510 G01 X0.184 Y0.126 C350.0 |
| N140 G01 X-0.202 Y-0.208 C13.0 | N560 G01 X-0.465 Y-1.089 C55.0 | N3520 G01 X0.165 Y0.115 C351.0 |
| N150 G01 X-0.216 Y-0.226 C14.0 | N570 G01 X-0.463 Y-1.111 C56.0 | N3530 G01 X0.146 Y0.104 C352.0 |
| N160 G01 X-0.229 Y-0.244 C15.0 | N580 G01 X-0.461 Y-1.133 C57.0 | N3540 G01 X0.127 Y0.092 C353.0 |
| N170 G01 X-0.242 Y-0.262 C16.0 | N590 G01 X-0.458 Y-1.155 C58.0 | N3550 G01 X0.108 Y0.080 C354.0 |
| N180 G01 X-0.254 Y-0.281 C17.0 | N600 G01 X-0.455 Y-1.178 C59.0 | N3560 G01 X0.089 Y0.067 C355.0 |
| N190 G01 X-0.266 Y-0.300 C18.0 | N610 G01 X-0.452 Y-1.200 C60.0 | N3570 G01 X0.071 Y0.054 C356.0 |
| N200 G01 X-0.278 Y-0.319 C19.0 | N620 G01 X-0.448 Y-1.222 C61.0 | N3580 G01 X0.053 Y0.041 C357.0 |
| N210 G01 X-0.290 Y-0.338 C20.0 | N630 G01 X-0.444 Y-1.244 C62.0 | N3590 G01 X0.035 Y0.028 C358.0 |
| N220 G01 X-0.301 Y-0.357 C21.0 | N640 G01 X-0.439 Y-1.266 C63.0 | N3600 G01 X0.017 Y0.014 C359.0 |
| N230 G01 X-0.312 Y-0.377 C22.0 | N650 G01 X-0.434 Y-1.287 C64.0 | N3610 G01 X0.000 Y0.000 C360.0 |
| N240 G01 X-0.323 Y-0.396 C23.0 | N660 G01 X-0.429 Y-1.309 C65.0 | |
| N250 G01 X-0.333 Y-0.416 C24.0 |  | G01 Z1 = 0 Z2 = 0 Z3 = 0 F50 |
| N260 G01 X-0.343 Y-0.436 C25.0 | G01 X0 F500 | |
| N270 G01 X-0.352 Y-0.457 C26.0 | G54 | |
| N280 G01 X-0.361 Y-0.477 C27.0 | G158 | |
| N290 G01 X-0.370 Y-0.498 C28.0 | M30 | |
| N300 G01 X-0.379 Y-0.518 C29.0 |
References
- Sun, Z.; To, S.; Zhang, S.; Zhang, G. Theoretical and experimental investigation into non-uniformity of surface generation in micro-milling. Int. J. Mech. Sci. 2018, 140, 313–324. [Google Scholar] [CrossRef]
- Yun, D.J.; Seo, T., II; Park, D.S. Fabrication of Biochips with Micro Fluidic Channels by Micro End-Milling and Powder Blasting. Sensors 2008, 8, 1308–1320. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.S.; Park, D.S. Microfabrication of Microchannels for Fuel Cell Plates. Sensors 2010, 10, 167–175. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Du, J.; Zhuang, X.; Wang, Z.; Pei, J. Geometric prediction of conic tool in micro-EDM milling with fix-length compensation using simulation. Int. J. Mach. Tools Manuf. 2015, 89, 86–94. [Google Scholar] [CrossRef]
- Chen, W.; Xie, W.; Huo, D.; Yang, K. A novel 3D surface generation model for micro milling based on homogeneous matrix transformation and dynamic regenerative effect. Int. J. Mech. Sci. 2018, 144, 146–157. [Google Scholar] [CrossRef]
- Romoli, L. Flattening of surface roughness in ultrashort pulsed laser micro-milling. Precis. Eng. 2018, 51, 331–337. [Google Scholar] [CrossRef]
- Fe, I.L.; Beruvides, G.; Quiza, R.; Haber, R.; Rivas, M. Automatic selection of optimal parameters based on simple soft computing methods. A case study on micro-milling processes. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Yuan, Y.; Jing, X.; Ehmann, K.F.; Cao, J.; Li, H.; Zhang, D. Modeling of cutting forces in micro end-milling. J. Manuf. Process. 2018, 31, 844–858. [Google Scholar] [CrossRef]
- López-Estrada, L.; Fajardo-Pruna, M.; Sánchez-González, L.; Pérez, H.; Vizán, A. Design and Implementation of a Vision System on an Innovative Single Point Micro-machining Device for Tool Tip Localization. In Proceedings of the International Joint Conference SOCO’17-CISIS’17-ICEUTE’17, León, Spain, 6–8 September 2017; pp. 219–228, ISBN 978-3-319-67179-6. [Google Scholar]
- Orra, K.; Choudhury, S.K. Mechanistic modelling for predicting cutting forces in machining considering effect of tool nose radius on chip formation and tool wear land. Int. J. Mech. Sci. 2018, 142–143, 255–268. [Google Scholar] [CrossRef]
- Chung, T.-K.; Yeh, P.-C.; Lee, H.; Lin, C.-M.; Tseng, C.-Y.; Lo, W.-T.; Wang, C.-M.; Wang, W.-C.; Tu, C.-J.; Tasi, P.-Y.; et al. An Attachable Electromagnetic Energy Harvester Driven Wireless Sensing System Demonstrating Milling-Processes and Cutter-Wear/Breakage-Condition Monitoring. Sensors 2016, 16, 269. [Google Scholar] [CrossRef] [PubMed]
- Richard, J.; Giandomenico, N. Electrode Profile Prediction and Wear Compensation in EDM-Milling and Micro-EDM-Milling. Procedia CIRP 2018, 68, 819–824. [Google Scholar] [CrossRef]
- Bai, J.; Bai, Q.; Tong, Z. Experimental and multiscale numerical investigation of wear mechanism and cutting performance of polycrystalline diamond tools in micro-end milling of titanium alloy Ti-6Al-4V. Int. J. Refract. Met. Hard Mater. 2018, 74, 40–51. [Google Scholar] [CrossRef]
- Zhu, K.; Yu, X. The monitoring of micro milling tool wear conditions by wear area estimation. Mech. Syst. Signal Process. 2017, 93, 80–91. [Google Scholar] [CrossRef]
- Szydłowski, M.; Powałka, B.; Matuszak, M.; Kochmański, P. Machine vision micro-milling tool wear inspection by image reconstruction and light reflectance. Precis. Eng. 2016, 44, 236–244. [Google Scholar] [CrossRef]
- Dai, Y.; Zhu, K. A machine vision system for micro-milling tool condition monitoring. Precis. Eng. 2018, 52, 183–191. [Google Scholar] [CrossRef]
- Chiou, R.Y.; Kwon, Y.; Tseng, T.-L.; Mauk, M. Experimental Study of High Speed CNC Machining Quality by Noncontact Surface Roughness Monitoring. Int. J. Mech. Eng. Robot. Res. 2015, 4, 282–286. [Google Scholar] [CrossRef]
- Pfeifer, T.; Sack, D.; Orth, A.; Stemmer, M.R.; Roloff, M. Measuring flank tool wear on cutting tools with machine vision—A case solution. In Proceedings of the IEEE Conference on Mechatronics and Machine Vision in Practice, Chiang Mai, Thailand, 10–12 September 2002; pp. 169–175. [Google Scholar]
- Fernández-Robles, L.; Azzopardi, G.; Alegre, E.; Petkov, N. Machine-vision-based identification of broken inserts in edge profile milling heads. Robot. Comput. Integr. Manuf. 2017, 44, 276–283. [Google Scholar] [CrossRef]
- Pérez, H.; Vizán, A.; Hernandez, J.C.; Guzmán, M. Estimation of cutting forces in micromilling through the determination of specific cutting pressures. J. Mater. Process. Technol. 2007, 190, 18–22. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Wang, W. Prediction of cutting forces and instantaneous tool deflection in micro end milling by considering tool run-out. Int. J. Mech. Sci. 2018, 136, 124–133. [Google Scholar] [CrossRef]
- Singh, T.; Dvivedi, A. On performance evaluation of textured tools during micro-channeling with ECDM. J. Manuf. Process. 2018, 32, 699–713. [Google Scholar] [CrossRef]
- Yu, X.; Lin, X.; Dai, Y.; Zhu, K. Image edge detection based tool condition monitoring with morphological component analysis. ISA Trans. 2017, 69, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Malamas, E.N.; Petrakis, E.G.; Zervakis, M.; Petit, L.; Legat, J.-D. A survey on industrial vision systems, applications and tools. Image Vis. Comput. 2003, 21, 171–188. [Google Scholar] [CrossRef]
- Fajardo-Pruna, M.; Márquez, J.; Rubio, M.; Vizán, A. Análisis Cinemático Inverso para un Mecanismo Paralelo 3—PRS. In Proceedings of the COLIM 2014 Memorias, Cuenca, Ecuador, 25–27 November 2014; pp. 824–829, ISBN 978-9978-10-201-5. [Google Scholar]
- Lai, Y.L.; Liao, C.C.; Chao, Z.G. Inverse kinematics for a novel hybrid parallel–serial five-axis machine tool. Robot. Comput. Integr. Manuf. 2018, 50, 63–79. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiu, K.; Wang, S.; Zhang, Z. Inverse kinematics and rigid-body dynamics for a three rotational degrees of freedom parallel manipulator. Robot. Comput. Integr. Manuf. 2015, 31, 40–50. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Chen, Q.; Wu, C.; Hu, X. Parasitic motion comparison of 3-PRS parallel mechanism with different limb arrangements. Robot. Comput. Integr. Manuf. 2011, 27, 389–396. [Google Scholar] [CrossRef]
- Fan, K.C.; Wang, H.; Zhao, J.W.; Chang, T.H. Sensitivity analysis of the 3-PRS parallel kinematic spindle platform of a serial-parallel machine tool. Int. J. Mach. Tools Manuf. 2003, 43, 1561–1569. [Google Scholar] [CrossRef]
- Shiau, T.-N.; Tsai, Y.-J.; Tsai, M.-S. Nonlinear dynamic analysis of a parallel mechanism with consideration of joint effects. Mech. Mach. Theory 2008, 43, 491–505. [Google Scholar] [CrossRef]
- Hornberg, A. Handbook of Machine Vision; Wiley-VCH: Hoboken, NJ, USA, 2006; ISBN 978-3-527-40584-8. [Google Scholar]
- Chaumette, F.; Hutchinson, S. Visual servo control. I. Basic approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Caprile, B.; Torre, V. Using vanishing points for camera calibration. Int. J. Comput. Vis. 1990, 4, 127–139. [Google Scholar] [CrossRef]
- Qidwai, U.; Chen, C.H. Digital Image Processing: An Algorithmic Approach with MATLAB; Chapman & Hall/CRC: Boca Raton, FL, USA, 2017; ISBN 978-1-138-11518-7. [Google Scholar]
- Huang, K.-Y.; Ye, Y.-T. A Novel Machine Vision System for the Inspection of Micro-Spray Nozzle. Sensors 2015, 15, 15326–15338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Yazdi, L.; Prabuwono, A.S.; Golkar, E. Feature extraction algorithm for fill level and cap inspection in bottling machine. In Proceedings of the 2011 International Conference on Pattern Analysis and Intelligence Robotics, Kuala Lumpur, Malaysia, 28–29 June 2011; Volume 1, pp. 47–52. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Tsai, M.-S.; Yuan, W.-H. Inverse dynamics analysis for a 3-PRS parallel mechanism based on a special decomposition of the reaction forces. Mech. Mach. Theory 2010, 45, 1491–1508. [Google Scholar] [CrossRef]
- Rokunuzzaman, M.; Jayasuriya, H.P.W. Development of a low cost machine vision system for sorting of tomatoes. Agric. Eng. Int. CIGR J. 2013, 15, 173–180. [Google Scholar]
- Elango, V.; Karunamoorthy, L. Effect of lighting conditions in the study of surface roughness by machine vision—An experimental design approach. Int. J. Adv. Manuf. Technol. 2008, 37, 92–103. [Google Scholar] [CrossRef]



















| Parameter | Description | Value |
|---|---|---|
| Radius of the fixed base | 180 mm | |
| Radius of the tool head | 80 mm | |
| Height of the start of axes | 630 mm | |
| Rod length | 200 mm | |
| Cutting tool length | 60 mm |
| Image | Image | Image | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0010 | −0.0008 | 16 | −0.0013 | 0.0028 | 31 | 0.0019 | 0.0024 |
| 2 | −0.0007 | 0.0001 | 17 | 0.0002 | 0.0006 | 32 | 0.0005 | 0.0005 |
| 3 | −0.0011 | −0.0016 | 18 | −0.0016 | 0.0020 | 33 | −0.0015 | −0.0013 |
| 4 | −0.0009 | 0.0001 | 19 | −0.0005 | 0.0024 | 34 | 0.0001 | −0.0014 |
| 5 | 0.0014 | 0.0029 | 20 | 0.0001 | 0.0020 | 35 | −0.0012 | 0.0016 |
| 6 | 0.0003 | 0.0024 | 21 | −0.0011 | 0.0023 | 36 | −0.0007 | 0.0020 |
| 7 | 0.0026 | −0.0013 | 22 | −0.0014 | 0.0021 | 37 | 0.0001 | 0.0002 |
| 8 | 0.0024 | 0.0006 | 23 | −0.0019 | 0.0028 | 38 | 0.0018 | −0.0002 |
| 9 | 0.0023 | −0.0012 | 24 | 0.0030 | −0.0002 | 39 | −0.0003 | 0.0009 |
| 10 | −0.0004 | 0.0020 | 25 | −0.0013 | 0.0016 | 40 | 0.0026 | 0.0020 |
| 11 | 0.0005 | 0.0002 | 26 | −0.0001 | 0.0003 | 41 | −0.0001 | −0.0017 |
| 12 | 0.0021 | −0.0001 | 27 | −0.0019 | −0.0005 | 42 | −0.0003 | 0.0026 |
| 13 | 0.0005 | 0.0028 | 28 | 0.0004 | 0.0005 | 43 | −0.0006 | 0.0025 |
| 14 | 0.0023 | −0.0001 | 29 | 0.0006 | 0.0003 | 44 | −0.0015 | 0.0023 |
| 15 | 0.0027 | 0.0012 | 30 | −0.0010 | 0.0008 | 45 | −0.0019 | 0.0022 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Estrada, L.; Fajardo-Pruna, M.; Sánchez-González, L.; Pérez, H.; Fernández-Robles, L.; Vizán, A. Design and Implementation of a Stereo Vision System on an Innovative 6DOF Single-Edge Machining Device for Tool Tip Localization and Path Correction. Sensors 2018, 18, 3132. https://doi.org/10.3390/s18093132
López-Estrada L, Fajardo-Pruna M, Sánchez-González L, Pérez H, Fernández-Robles L, Vizán A. Design and Implementation of a Stereo Vision System on an Innovative 6DOF Single-Edge Machining Device for Tool Tip Localization and Path Correction. Sensors. 2018; 18(9):3132. https://doi.org/10.3390/s18093132
Chicago/Turabian StyleLópez-Estrada, Luis, Marcelo Fajardo-Pruna, Lidia Sánchez-González, Hilde Pérez, Laura Fernández-Robles, and Antonio Vizán. 2018. "Design and Implementation of a Stereo Vision System on an Innovative 6DOF Single-Edge Machining Device for Tool Tip Localization and Path Correction" Sensors 18, no. 9: 3132. https://doi.org/10.3390/s18093132
APA StyleLópez-Estrada, L., Fajardo-Pruna, M., Sánchez-González, L., Pérez, H., Fernández-Robles, L., & Vizán, A. (2018). Design and Implementation of a Stereo Vision System on an Innovative 6DOF Single-Edge Machining Device for Tool Tip Localization and Path Correction. Sensors, 18(9), 3132. https://doi.org/10.3390/s18093132