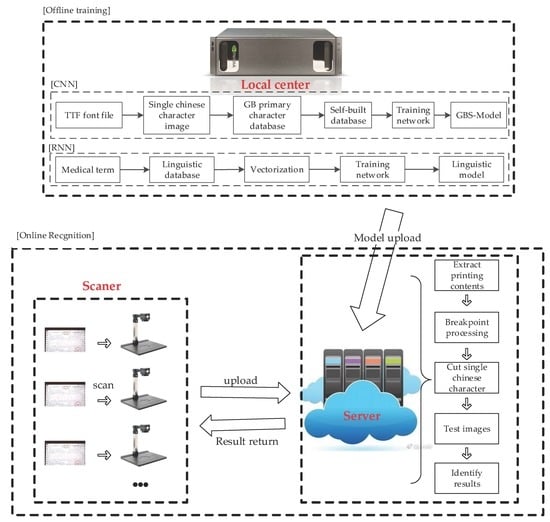
In the first module, we only needed two models trained by Alexnet-Adam-CNN and RNN. Then, we could upload these models to the cloud and save it.
In the second module, as there is a large amount of professional terminology in medical invoices, this paper combined AA-CNN and RNN in sequence. After AA-CNN outputs recognized the results, RNN was used to carry out the semantic revisions obtained by the recognized results of CNN, and modified some professional terminology in the medical invoices.
3.1. AA-CNN Model Training for Recognition
After obtaining the font images of the medical invoices, we carried out the image preprocessing in order to obtain the training set required by the AA-CNN network, which integrates the Alexnet and Adam optimization algorithm, and we started network training with the primary character dataset. In the end, we could save the trained model to the local and identify the images. The specific process is shown in
Figure 2.
First, we got the single Chinese character images from the TTF font file, then we put all of these images together to form a primary character dataset, which included 525,700 images from 3755 commonly used Chinese characters.
Second, because of the differences between the common invoices and medical ones, we added the appropriate percentage of simulated breakpoint fonts to build a new dataset, which included 225,300 images from 3755 commonly used Chinese characters.
In view of the different fonts between the normal notes and medical invoices, we designed a method to imitate the breakpoint font. The comparison of these two kinds of invoices is shown in
Figure 3.
We can clearly see from
Figure 4 that the font of the general invoice is continuous, while the medical one is broken.
Therefore, we simulated the breakpoint effect on the original font according to the principle of the printing breakpoint font, and used them to form a new dataset (self-built dataset), which included 751,000 images—525,700 images from the primary dataset, and 225,300 images from the new dataset (this kind of structure will be explained in
Section 4.3.1). It is shown in
Figure 5.
To illustrate our figure clearly, we added English translations to help understand the figure. At the left side is an example of the original dataset (
https://github.com/AstarLight/CPS-OCR-Engine/blob/master/ocr/gen_printed_char.py). The Chinese character on the image means “content” in English. On the right side is an example of the Chinese characters from our self-built dataset—the meanings of the Chinese characters are “great”, “real”, “time”, “boy”, “modest”, and “normal”. Both datasets are expanded by rotating at different angels.
Finally, as we already know that so many CNN models have been used in many other areas, in order to find an appropriate one, we used some known CNNs, such as Googlenet, Caffenet, and Alexnet, to select a better network that is suitable for our goal.
From the data shown in
Table 1, we can see that Alexnet has a higher accuracy when distinguishing the medical invoices; therefore, we chose Alexnet to continue further with our experiment.
During the Alexnet training, any change of the parameters in a layer would result in changes in the following parameters, leading to the network needing to constantly adapt to the new data distribution. It required more parameters to adjust the vector, and it was harder to train a network because of the existence of the nonlinear problems in the activation function of the operation. From what we discussed above, the input data of each layer of the neural network were normalized to the standard normal distribution, which can solve the problems above, reduce the training time of the network significantly, and accelerate the network convergence effectively.
For further improving accuracy and reducing loss, in the second stage, image preprocessing methods such as binarization were added to obtain a small sample dataset, and the training was conducted again.
We used AA-CNN to train the character dataset and the Relu activation function to reduce the computing costs. The Relu equation is shown in Equation (1):
Next, we will explain how the AA-CNN network worked.
As shown in
Figure 6, a Chinese character image with a size of 300 × 300 pixels was input into the input layer, and then, after five convolutions (the kernel size of the first convolutional layer was 11 × 11 pixels, while the others’ kernel size was 3 × 3 pixels) and two max-poolings connected to two fully-connected layers, and it finally output 3755 categories—the validation split value was 375,500 and the batch size was 128.
In this article we chose Alexnet in order to make this network more suitable for training the self-built dataset. We made a series of modifications to it, such as the kernel size of the convolutional layer. We also used the Adam optimization algorithm to further reduce the loss value of Alexnet.
The reasons for using AA-CNN for training in this paper were as follows:
Local connection and weight sharing: to reduce a large number of parameters, the speed of seal recognition, and classification;
Downsampling: to improve the robustness of the model, that is, to improve the accuracy of the medical invoice recognition and model stability;
Local response normalization: this normalization was applied after using the nonlinear activation function of ReLu;
Overlapping pooling: to reduce the overfitting of images caused by the operation of the non-overlapping adjacent units.
At the same time, three different optimization algorithms were selected based on the Alexnet network, which were as follows:
SGD optimization algorithm;
Adam optimization algorithm;
AdaGrad optimization algorithm.
In
Figure 7, we can see the Adam optimization algorithm (Adam curve: train “accuracy/train” loss, SGD curve: train accuracy/train loss, AdaGrad curve: train accuracy’’’/train loss’’’)—the loss rate was reduced and the recognition accuracy was improved.
In the procedure of the back propagation, the chain rule was applied on the loss function. The normalized layer was determined by the type of back propagation gradient, including a summation calculation with a small data batch. The calculation equation is shown below:
3.2. RNN Model Training for Semantic Revisions
This paper introduced the optimization and acceleration of the BPTT-RNN model from the following aspects. The framework is shown in
Figure 8.
First, we downloaded the medical terminology from the CNKI (China National Knowledge Infrastructure) and PubMed, making the linguistic dataset include more than 7000 medical terms.
Then, we needed to vectorize the linguistic dataset, preparing for network training.
Finally, in order to obtain the linguistic model, the dataset was applied on the network training.
The RNN was applied to do the semantic revisions using the results of CNN. Then, we gave a brief introduction of BPTT-RNN.
The circulation layer structure is shown in
Figure 9.
As is shown in
Figure 9, the output of the hidden layer was
ot using
xt as input data. The point is, the value of
s depended not just on
xt, but on
st−1. We can use the following equations to express the calculation procedure of cyclic neural network:
Equation (5) is the output layer calculation function. The output layer was a full connection layer. V is the weight matrix of the output layer, and g is the activation function. Equation (6) is the hidden layer (circulation layer) calculation function. U is the weight matrix for the input x, W is the value for the last time, st−1 is the input weight matrix for this time, and f is the activation function (ReLU).
The BPTT algorithm is a training algorithm for a cyclic layer. Its basic principle is the same as the BP algorithm, and it also contains the same three steps:
Forward calculation of each neuron output value;
The error term
value of each neuron is calculated reversely. It is the partial derivative of the error function E to the weighted input of the neuron j;
Calculate the gradient of each weight.
Finally, we used the stochastic gradient descent algorithm to update the weight, using the previous Equation (6) to carry out forward calculation for the circulation layer:
Then, we expanded Equation (6) to get Equation (7):
The left side of Equation (7) is an output vector, st, with a size of n.
The right side of Equation (7) has an input vector, x, with a size of m; the dimension of matrix U is n*m; and the dimension of matrix W is n*n.
represents the value of the nth element of the vector s at time t, unm means the weight from the mth neuron in the input layer to the nth neuron in the circulation layer, and wnn means the weight from the nth neuron at time t−1 of the circulation layer to the nth neuron at time t of the circulation layer.
3.3. Recognition
After the CNN and RNN model training, the recognition module could carry out the offline operation. The specific procedure is shown in
Figure 10.
We got the image of the original medical invoice obtained by a scanner, then extracted the parts we needed to identify through the color threshold.
Finally, extracted text preprocessing (breakpoint processing) was performed. Breakpoint processing is a process with two steps. The first one is Gaussian blur (in this paper, a Gaussian blur with a 0.3 pixel radius was adopted for the medical invoices). The Gaussian blur equations are shown as follows:
In the equations above, means the radius of the pixels, the radius of the Gaussian distribution (σ) is 0.5, μ is the central point, which is generally zero, and (x,y) are the relative coordinates of the peripheral pixels to the center ones. In Equation (8), f(x) is the density function of the normal distribution in one dimension, also known as the Gaussian distribution. In Equation (9), G(x,y) is the two-dimensional Gaussian equation derived from Equation (8).
After the Gaussian blur processing, the image was further enhanced by a smoothing operation. In order to get a clearer outline (high frequency and intermediate frequency information of the image) of the breakpoint font, we used the mean value filtering to process the image after the Gaussian blur. The equations are shown in Equations (10) and (11):
A kernel with the size of m*n (m, n is odd) was applied on the image as the mean filtering, and the value of the intermediate pixel was replaced by the pixel average of the region covered by the kernel, g(x, y) means the center point at (x, y) with the size of the m*n filter window, and f (s,t) means the activation function. It is calculated as Equation (10).
For the images of size M*N, the weighted mean filter whose window was the size of M*N is calculated as Equation (11).