Skin Strain Analysis of the Scapular Region and Wearables Design
Abstract
:1. Introduction
2. Scapular Movements and Effects of Underlying Soft Tissue on Strain Distribution
3. Materials and Methods
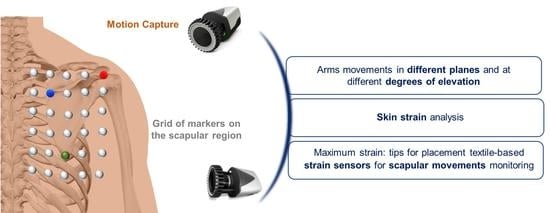
3.1. Participants
3.2. Experimental Set-Up
3.3. Experimental Protocol
- Task 1: 10 consecutive arm abductions in the frontal plane from starting position to approximately 90°.
- Task 2: 10 consecutive arm abductions in the frontal plane from starting position to maximum elevation.
- Task 3: 10 consecutive arm flexions in the sagittal plane from starting position to approximately 90°.
- Task 4: 10 consecutive arm flexions in the sagittal plane from starting position to maximum elevation.
- Task 5: 10 consecutive arm elevations in the scapular plane from starting position to approximately 90°.
- Task 6: 10 consecutive arm elevations in the scapular plane from starting position to maximum elevation.
3.4. Data Analysis
3.4.1. Motion Capture Data
3.4.2. Skin Deformation Analysis and Statistics
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Longo, U.G.; Risi Ambrogioni, L.; Berton, A.; Candela, V.; Massaroni, C.; Carnevale, A.; Stelitano, G.; Schena, E.; Nazarian, A.; DeAngelis, J.; et al. Scapular Dyskinesis: From Basic Science to Ultimate Treatment. Int. J. Environ. Res. Public Health 2020, 17, 2974. [Google Scholar]
- Longo, U.G.; Carnevale, A.; Massaroni, C.; Lo Presti, D.; Berton, A.; Candela, V.; Schena, E.; Denaro, V. Personalized, Predictive, Participatory, Precision, and Preventive (P5) Medicine in Rotator Cuff Tears. J. Pers. Med. 2021, 11, 255. [Google Scholar] [CrossRef]
- Rockwood, C.A. The Shoulder; Elsevier Health Sciences: Amsterdam, The Netherlands, 2009; Volume 1. [Google Scholar]
- Kibler, B.W.; McMullen, J. Scapular dyskinesis and its relation to shoulder pain. J. Am. Acad. Orthop. Surg. 2003, 11, 142–151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Terry, G.C.; Chopp, T.M. Functional anatomy of the shoulder. J. Athl. Train. 2000, 35, 248. [Google Scholar]
- Wang, J.; Lu, C.; Zhang, K. Textile-based strain sensor for human motion detection. Energy Environ. Mater. 2020, 3, 80–100. [Google Scholar] [CrossRef] [Green Version]
- Carnevale, A.; Tocco, J.d.; Massaroni, C.; Longo, U.G.; Schena, E.; Denaro, V. Polymer-encapsulated flexible strain sensors to monitor scapular movement: A pilot study. In Proceedings of the 2021 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0&IoT), Rome, Italy, 7–9 June 2021; pp. 213–218. [Google Scholar]
- Semjonova, G.; Vetra, J.; Cauce, V.; Oks, A.; Katashev, A.; Eizentals, P. Improving the Recovery of Patients with Subacromial Pain Syndrome with the DAid Smart Textile Shirt. Sensors 2020, 20, 5277. [Google Scholar] [CrossRef]
- Eizentals, P.; Katashev, A.; Oks, A.; Semjonova, G. Smart shirt system for compensatory movement retraining assistance: Feasibility study. Health Technol. 2020, 10, 861–874. [Google Scholar] [CrossRef]
- Crowe, M.M.; Elhassan, B.T. Scapular and shoulder girdle muscular anatomy: Its role in periscapular tendon transfers. J. Hand Surg. 2016, 41, 306–314. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.W.; Kim, Y.I.; Kim, H.Y.; Yang, D.S.; Lee, G.S.; Choy, W.S. Three-dimensional scapular kinematics in patients with reverse total shoulder arthroplasty during arm motion. Clin. Orthop. Surg. 2016, 8, 316–324. [Google Scholar] [CrossRef] [Green Version]
- Walker, D.; Matsuki, K.; Struk, A.M.; Wright, T.W.; Banks, S.A. Scapulohumeral rhythm in shoulders with reverse shoulder arthroplasty. J. Shoulder Elb. Surg. 2015, 24, 1129–1134. [Google Scholar] [CrossRef] [PubMed]
- Mattson, J.M.; Russo, S.A.; Rose, W.C.; Rowley, K.M.; Richards, J.G. Identification of scapular kinematics using surface mapping: A validation study. J. Biomech. 2012, 45, 2176–2179. [Google Scholar] [CrossRef] [Green Version]
- Zaferiou, A.M.; Knowlton, C.B.; Jang, S.-H.; Saltzman, B.; Verma, N.; Forsythe, B.; Nicholson, G.; Romeo, A.A. Patient-specificity of scapular orientation measurements using an acromion marker cluster with multiple calibration poses. J. Biomech. 2020, 108, 109889. [Google Scholar] [CrossRef] [PubMed]
- Bourne, D.A.; Choo, A.M.; Regan, W.D.; MacIntyre, D.L.; Oxland, T.R. The placement of skin surface markers for non-invasive measurement of scapular kinematics affects accuracy and reliability. Ann. Biomed. Eng. 2011, 39, 777–785. [Google Scholar] [CrossRef] [PubMed]
- Lempereur, M.; Brochard, S.; Leboeuf, F.; Rémy-Néris, O. Validity and reliability of 3D marker based scapular motion analysis: A systematic review. J. Biomech. 2014, 47, 2219–2230. [Google Scholar] [CrossRef]
- Matsuki, K.; Matsuki, K.O.; Mu, S.; Yamaguchi, S.; Ochiai, N.; Sasho, T.; Sugaya, H.; Toyone, T.; Wada, Y.; Takahashi, K. In vivo 3-dimensional analysis of scapular kinematics: Comparison of dominant and nondominant shoulders. J. Shoulder Elb. Surg. 2011, 20, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Valevicius, A.M.; Jun, P.Y.; Hebert, J.S.; Vette, A.H. Use of optical motion capture for the analysis of normative upper body kinematics during functional upper limb tasks: A systematic review. J. Electromyogr. Kinesiol. 2018, 40, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Faisal, A.I.; Majumder, S.; Mondal, T.; Cowan, D.; Naseh, S.; Deen, M.J. Monitoring methods of human body joints: State-of-the-art and research challenges. Sensors 2019, 19, 2629. [Google Scholar] [CrossRef] [Green Version]
- Carnevale, A.; Longo, U.G.; Schena, E.; Massaroni, C.; Presti, D.L.; Berton, A.; Candela, V.; Denaro, V. Wearable systems for shoulder kinematics assessment: A systematic review. BMC Musculoskelet. Disord. 2019, 20, 546. [Google Scholar] [CrossRef]
- Carnevale, A.; Massaroni, C.; Presti, D.L.; Formica, D.; Longo, U.G.; Schena, E.; Denaro, V. Wearable stretchable sensor based on conductive textile fabric for shoulder motion monitoring. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Rome, Italy, 3–5 June 2020; pp. 106–110. [Google Scholar]
- Lorussi, F.; Carbonaro, N.; De Rossi, D.; Paradiso, R.; Veltink, P.; Tognetti, A. Wearable textile platform for assessing stroke patient treatment in daily life conditions. Front. Bioeng. Biotechnol. 2016, 4, 28. [Google Scholar] [CrossRef]
- Lo Presti, D.; Carnevale, A.; D’Abbraccio, J.; Massari, L.; Massaroni, C.; Sabbadini, R.; Zaltieri, M.; Di Tocco, J.; Bravi, M.; Miccinilli, S. A multi-parametric wearable system to monitor neck movements and respiratory frequency of computer workers. Sensors 2020, 20, 536. [Google Scholar] [CrossRef] [Green Version]
- Lorussi, F.; Carbonaro, N.; De Rossi, D.; Tognetti, A. A bi-articular model for scapular-humeral rhythm reconstruction through data from wearable sensors. J. Neuroeng. Rehabil. 2016, 13, 40. [Google Scholar] [CrossRef]
- Lorussi, F.; Lucchese, I.; Tognetti, A.; Carbonaro, N. A wearable system for remote monitoring of the treatments of musculoskeletal disorder. In Proceedings of the 2018 IEEE International Conference on Smart Computing (SMARTCOMP), Taormina, Italy, 18–20 June 2018; pp. 362–367. [Google Scholar]
- Wessendorf, A.M.; Newman, D.J. Dynamic understanding of human-skin movement and strain-field analysis. IEEE Trans. Biomed. Eng. 2012, 59, 3432–3438. [Google Scholar] [CrossRef]
- Lin, B.; Moerman, K.M.; McMahan, C.G.; Pasch, K.A.; Herr, H.M. Low-cost methodology for skin strain measurement of a flexed biological limb. IEEE Trans. Biomed. Eng. 2016, 64, 2750–2759. [Google Scholar]
- Hu, Z.; Liu, L.; Liu, Z.; Xing, M. Dynamic Understanding of Human-Skin Movement and Garment Design of Golf Apparel. In Proceedings of the International Conference on Applied Human Factors and Ergonomics, Los Angeles, CA, USA, 17–21 July 2017; Springer: Cham, Switzerland, 2017; pp. 982–994. [Google Scholar]
- Barrios-Muriel, J.; Romero Sánchez, F.; Alonso Sánchez, F.J.; Rodríguez Salgado, D. In vivo measurement of surface skin strain during human gait to improve the design of rehabilitation devices. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 1219–1228. [Google Scholar] [CrossRef]
- Obropta, E.W.; Newman, D.J. Skin strain fields at the shoulder joint for mechanical counter pressure space suit development. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–9. [Google Scholar]
- Roche, S.J.; Funk, L.; Sciascia, A.; Kibler, W.B. Scapular dyskinesis: The surgeon’s perspective. Shoulder Elb. 2015, 7, 289–297. [Google Scholar] [CrossRef] [Green Version]
- Neumann, D.A.; Camargo, P.R. Kinesiologic considerations for targeting activation of scapulothoracic muscles—Part 1: Serratus anterior. Braz. J. Phys. Ther. 2019, 23, 459–466. [Google Scholar] [CrossRef]
- Camargo, P.R.; Neumann, D.A. Kinesiologic considerations for targeting activation of scapulothoracic muscles—Part 2: Trapezius. Braz. J. Phys. Ther. 2019, 23, 467–475. [Google Scholar] [CrossRef]
- Carnevale, A.; Massaroni, C.; Presti, D.L.; Di Tocco, J.; Zaltieri, M.; Formica, D.; Longo, U.G.; Schena, E.; Denaro, V. Conductive textile element embedded in a wearable device for joint motion monitoring. In Proceedings of the 2020 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Bari, Italy, 1 June–1 July 2020; pp. 1–6. [Google Scholar]
- Di Tocco, J.; Carnevale, A.; Bravi, M.; Longo, U.G.; Sterzi, S.; Massaroni, C.; Schena, E. Wearable system for elbow angles estimation based on a polymer encapsulated conductive textile. In Proceedings of the 2021 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4. 0&IoT), Rome, Italy, 7–9 June 2021; pp. 473–477. [Google Scholar]
- Wang, Q.; De Baets, L.; Timmermans, A.; Chen, W.; Giacolini, L.; Matheve, T.; Markopoulos, P. Motor control training for the shoulder with smart garments. Sensors 2017, 17, 1687. [Google Scholar] [CrossRef] [PubMed]
- Esfahani, M.I.M.; Nussbaum, M.A. A “Smart” undershirt for tracking upper body motions: Task classification and angle estimation. IEEE Sens. J. 2018, 18, 7650–7658. [Google Scholar] [CrossRef]









| Volunteer | Age [years] | Body Mass [kg] | Height [m] | BMI [kg∙m−2] |
|---|---|---|---|---|
| V1 | 24 | 81 | 1.73 | 27.1 |
| V2 | 24 | 83 | 1.89 | 23.2 |
| V3 | 25 | 67 | 1.72 | 22.6 |
| V4 | 32 | 62 | 1.63 | 23.3 |
| V5 | 22 | 81 | 1.90 | 22.4 |
| Mean [–] | SD [–] | Median [–] | Min [–] | Max [–] | SW p-Value | W p-Value | |
|---|---|---|---|---|---|---|---|
| Fro90 | −0.46 | 6.43 | −0.80 | −20.54 | 28.26 | <0.001 a | 0.002 b |
| FroMax | −0.36 | 13.27 | −4.05 | −30.72 | 52.95 | <0.001 a | |
| Sag90 | 5.37 | 11.59 | 2.55 | −16.16 | 60.12 | <0.001 a | <0.001 b |
| SagMax | 0.69 | 14.62 | −3.96 | −25.52 | 60.87 | <0.001 a | |
| Scap90 | 1.86 | 7.94 | −0.60 | −14.91 | 40.89 | <0.001 a | <0.001 b |
| ScapMax | 0.32 | 11.08 | −2.96 | −24.54 | 48.19 | <0.001 a |
| Elevation 90° | Max Elevation | |||
|---|---|---|---|---|
| Pair of Markers | Pair of Markers | |||
| Extension | 19–20 | 28.26 | 19–20 | 52.95 |
| 25–29 | 21.32 | 25–29 | 49.07 | |
| 18–20 | 21.16 | 25–28 | 44.08 | |
| 20–24 | 20.97 | 20–24 | 42.65 | |
| 20–23AI | 20.00 | 20–23AI | 40.90 | |
| Compression | 3–5AA | −20.54 | 2–5AA | −30.72 |
| 4–5AA | −19.70 | 3–5AA | −30.51 | |
| 2–5AA | −18.95 | 1–5AA | −30.44 | |
| 1–5AA | −18.37 | 4–5AA | −26.92 | |
| 3–4 | −16.14 | 3–4 | −24.17 | |
| Elevation 90° | Max Elevation | |||
|---|---|---|---|---|
| Pair of Markers | Pair of Markers | |||
| Extension | 19–20 | 60.12 | 19–20 | 60.87 |
| 18–20 | 42.51 | 25–29 | 48.91 | |
| 14–15 | 38.63 | 25–28 | 45.77 | |
| 20–23AI | 37.48 | 18–20 | 44.06 | |
| 20–24 | 36.91 | 20–24 | 43.74 | |
| Compression | 15–20 | −16.16 | 2–5AA | −25.52 |
| 9–14 | −12.83 | 1–5AA | −24.95 | |
| 9–19 | −12.31 | 3–5AA | −24.44 | |
| 14–19 | −12.15 | 4–5AA | −22.06 | |
| 19–30 | −12.05 | 18–23AI | −21.63 | |
| Elevation 90° | Max Elevation | |||
|---|---|---|---|---|
| Pair of Markers | Pair of Markers | |||
| Extension | 19–20 | 40.89 | 19–20 | 48.20 |
| 18–20 | 31.69 | 25–29 | 39.52 | |
| 20–23AI | 27.84 | 20–24 | 37.93 | |
| 20–24 | 27.03 | 25–28 | 35.34 | |
| 25–29 | 26.15 | 18–20 | 35.13 | |
| Compression | 15–20 | −14.91 | 3–5AA | −24.54 |
| 4–5AA | −13.35 | 2–5AA | −24.45 | |
| 3–5AA | −13.08 | 1–5AA | −24.04 | |
| 2–5AA | −12.00 | 4–5AA | −21.43 | |
| 1–5AA | −11.57 | 5AA-6 | −18.16 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carnevale, A.; Schena, E.; Formica, D.; Massaroni, C.; Longo, U.G.; Denaro, V. Skin Strain Analysis of the Scapular Region and Wearables Design. Sensors 2021, 21, 5761. https://doi.org/10.3390/s21175761
Carnevale A, Schena E, Formica D, Massaroni C, Longo UG, Denaro V. Skin Strain Analysis of the Scapular Region and Wearables Design. Sensors. 2021; 21(17):5761. https://doi.org/10.3390/s21175761
Chicago/Turabian StyleCarnevale, Arianna, Emiliano Schena, Domenico Formica, Carlo Massaroni, Umile Giuseppe Longo, and Vincenzo Denaro. 2021. "Skin Strain Analysis of the Scapular Region and Wearables Design" Sensors 21, no. 17: 5761. https://doi.org/10.3390/s21175761
APA StyleCarnevale, A., Schena, E., Formica, D., Massaroni, C., Longo, U. G., & Denaro, V. (2021). Skin Strain Analysis of the Scapular Region and Wearables Design. Sensors, 21(17), 5761. https://doi.org/10.3390/s21175761