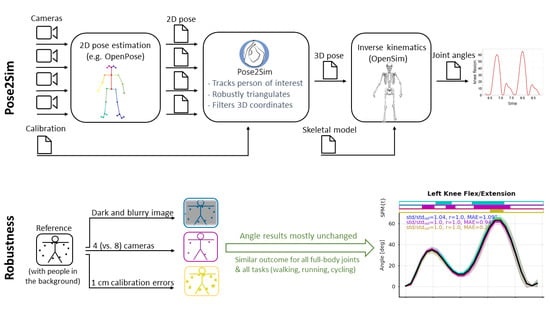
Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness
Abstract
:1. Introduction
1.1. Overall Context
1.2. 2D Pose Estimation
1.3. 2D Kinematics from 2D Pose Estimation
1.4. 3D Pose Estimation
1.5. 3D Kinematics from 3D Pose Estimation
1.6. Robustness of Deep-Learning Approaches
1.7. Objectives of the Study
2. Materials and Methods
2.1. Data Collection
2.1.1. Experimental Setup
2.1.2. Participant and Protocol
- Walking: The subject walked in a straight line back and forth over the 10 m diagonal of the room. His body mesh could be fully reconstructed only in the central 5 m of the acquisition space, i.e., only roughly 2 gait cycles were acquired per walking line. His comfortable stride pace was 100 BPM (Beats per Minute). The stride length was not monitored.
- Running: The subject jogged in a straight line back and forth along the 10m diagonal of the room. His comfortable stride pace was 150 BPM (Beats per Minute). The stride length was not monitored.
- Cycling: The subject cycled on a road bike placed on a home trainer. He himself adjusted the resistance and the height of the saddle prior to the capture. His comfortable cadence was 60 BPM.
2.2. The Reference Condition and the Three Degraded
2.2.1. Reference Condition (Ref)
2.2.2. Poor Image Quality (Im)
2.2.3. Less Cameras (4c)
2.2.4. Calibration Errors (Cal)
2.3. OpenPose: 2D Pose Estimation
2.4. Pose2Sim: 3D Pose Estimation Toolbox
2.4.1. Tracking the Person of Interest
2.4.2. Triangulation
2.4.3. Filtering
2.5. OpenSim: Joint Angle Calculations
2.5.1. Gait Events
2.5.2. Model Definition
2.5.3. Model Scaling
- Arm: pairs (left shoulder, left elbow) and (right shoulder, right elbow);
- Forearm: pairs (left elbow, left wrist) and (right elbow, right wrist);
- Thigh: pairs (left hip, left knee) and (right hip, right knee);
- Shank: pairs (left knee, left ankle) and (right knee, right ankle);
- Foot: pairs (left heel, left big toe) and (right heel, right big toe);
- Pelvis: pair (right hip, left hip);
- Torso: pairs (neck, right hip) and (neck, left hip);
- Head: pairs (head, nose);
2.5.4. Inverse Kinematics
2.6. Statistical Analysis
3. Results
3.1. Data Collection and 2D Pose Estimation
3.2. Pose2Sim Tracking, Triangulation, and Filtering
3.3. OpenSim Scaling and Inverse Kinematics
3.4. Relevance, Repeatability and Robustness of Angles Results
4. Discussion
4.1. Pose2Sim
4.2. Relevance, Repeatibility, and Robustness
4.3. Limitations and Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Running Task

Appendix B. Cycling Task

References
- Mündermann, L.; Corazza, S.; Andriacchi, T.P. The Evolution of Methods for the Capture of Human Movement Leading to Markerless Motion Capture for Biomechanical Applications. J. NeuroEng. Rehabil. 2006, 3, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Topley, M.; Richards, J.G. A Comparison of Currently Available Optoelectronic Motion Capture Systems. J. Biomech. 2020, 106, 109820. [Google Scholar] [CrossRef] [PubMed]
- Tsushima, H.; Morris, M.E.; McGinley, J. Test-Retest Reliability and Inter-Tester Reliability of Kinematic Data from a Three-Dimensional Gait Analysis System. J. Jpn. Phys. Ther. Assoc. 2003, 6, 9–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Della Croce, U.; Cappozzo, A.; Kerrigan, D.C. Pelvis and Lower Limb Anatomical Landmark Calibration Precision and Its Propagation to Bone Geometry and Joint Angles. Med. Biol. Eng. Comput. 1999, 37, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Gorton, G.E.; Hebert, D.A.; Gannotti, M.E. Assessment of the Kinematic Variability among 12 Motion Analysis Laboratories. Gait Posture 2009, 29, 398–402. [Google Scholar] [CrossRef] [PubMed]
- Benoit, D.L.; Damsgaard, M.; Andersen, M.S. Surface Marker Cluster Translation, Rotation, Scaling and Deformation: Their Contribution to Soft Tissue Artefact and Impact on Knee Joint Kinematics. J. Biomech. 2015, 48, 2124–2129. [Google Scholar] [CrossRef]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and Orientation in Space of Bones during Movement: Anatomical Frame Definition and Determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Leboeuf, F.; Reay, J.; Jones, R.; Sangeux, M. The Effect on Conventional Gait Model Kinematics and Kinetics of Hip Joint Centre Equations in Adult Healthy Gait. J. Biomech. 2019, 87, 167–171. [Google Scholar] [CrossRef]
- Zhang, J.-T.; Novak, A.C.; Brouwer, B.; Li, Q. Concurrent Validation of Xsens MVN Measurement of Lower Limb Joint Angular Kinematics. Physiol. Meas. 2013, 34, N63–N69. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghazilla, R.A.R.; Khairi, N.M.; Kasi, V. Reviews on Various Inertial Measurement Unit (IMU) Sensor Applications. IJSPS 2013, 256–262. [Google Scholar] [CrossRef] [Green Version]
- Carraro, M.; Munaro, M.; Burke, J.; Menegatti, E. Real-Time Marker-Less Multi-Person 3D Pose Estimation in RGB-Depth Camera Networks. arXiv 2017, arXiv:1710.06235. [Google Scholar]
- Choppin, S.; Wheat, J. The Potential of the Microsoft Kinect in Sports Analysis and Biomechanics. Sports Technol. 2013, 6, 78–85. [Google Scholar] [CrossRef]
- Colombel, J.; Bonnet, V.; Daney, D.; Dumas, R.; Seilles, A.; Charpillet, F. Physically Consistent Whole-Body Kinematics Assessment Based on an RGB-D Sensor. Application to Simple Rehabilitation Exercises. Sensors 2020, 20, 2848. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Shao, L.; Xu, D.; Shotton, J. Enhanced Computer Vision With Microsoft Kinect Sensor: A Review. IEEE Trans. Cybern. 2013, 43, 1318–1334. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Tan, S.; Zhen, X.; Xu, S.; Zheng, F.; He, Z.; Shao, L. Deep 3D Human Pose Estimation: A Review. Comput. Vis. Image Underst. 2021, 210, 103225. [Google Scholar] [CrossRef]
- Baker, R. The History of Gait Analysis before the Advent of Modern Computers. Gait Posture 2007, 26, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Cronin, N.J. Using Deep Neural Networks for Kinematic Analysis: Challenges and Opportunities. J. Biomech. 2021, 123, 110460. [Google Scholar] [CrossRef]
- Seethapathi, N.; Wang, S.; Saluja, R.; Blohm, G.; Kording, K.P. Movement Science Needs Different Pose Tracking Algorithms. arXiv 2019, arXiv:1907.10226. [Google Scholar]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.-E.; Sheikh, Y. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. arXiv 2019, arXiv:1812.08008. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.-S.; Xie, S.; Tai, Y.-W.; Lu, C. RMPE: Regional Multi-Person Pose Estimation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2353–2362. [Google Scholar]
- Joo, H.; Liu, H.; Tan, L.; Gui, L.; Nabbe, B.; Matthews, I.; Kanade, T.; Nobuhara, S.; Sheikh, Y. Panoptic Studio: A Massively Multiview System for Social Motion Capture. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3334–3342. [Google Scholar]
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless Pose Estimation of User-Defined Body Parts with Deep Learning. Nat. Neurosci. 2018, 21, 1281–1289. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, Y.; He, M. Monocular Human Pose Estimation: A Survey of Deep Learning-Based Methods. Comput. Vis. Image Underst. 2020, 192, 102897. [Google Scholar] [CrossRef]
- Kidziński, Ł.; Yang, B.; Hicks, J.L.; Rajagopal, A.; Delp, S.L.; Schwartz, M.H. Deep Neural Networks Enable Quantitative Movement Analysis Using Single-Camera Videos. Nat. Commun. 2020, 11, 4054. [Google Scholar] [CrossRef] [PubMed]
- Stenum, J.; Rossi, C.; Roemmich, R.T. Two-Dimensional Video-Based Analysis of Human Gait Using Pose Estimation. PLoS Comput. Biol. 2021, 17, e1008935. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Yu, S.; An, W.; Huang, Y. A Model-Based Gait Recognition Method with Body Pose and Human Prior Knowledge. Pattern Recognit. 2020, 98, 107069. [Google Scholar] [CrossRef]
- Viswakumar, A.; Rajagopalan, V.; Ray, T.; Parimi, C. Human Gait Analysis Using OpenPose. In Proceedings of the 2019 Fifth International Conference on Image Information Processing (ICIIP), Waknaghat, India, 15–17 November 2019; pp. 310–314. [Google Scholar]
- Drazan, J.F.; Phillips, W.T.; Seethapathi, N.; Hullfish, T.J.; Baxter, J.R. Moving Outside the Lab: Markerless Motion Capture Accurately Quantifies Sagittal Plane Kinematics during the Vertical Jump. J. Biomech. 2021, 125, 110547. [Google Scholar] [CrossRef] [PubMed]
- Cronin, N.J.; Rantalainen, T.; Ahtiainen, J.P.; Hynynen, E.; Waller, B. Markerless 2D Kinematic Analysis of Underwater Running: A Deep Learning Approach. J. Biomech. 2019, 87, 75–82. [Google Scholar] [CrossRef]
- Serrancolí, G.; Bogatikov, P.; Huix, J.P.; Barberà, A.F.; Egea, A.J.S.; Ribé, J.T.; Kanaan-Izquierdo, S.; Susín, A. Marker-Less Monitoring Protocol to Analyze Biomechanical Joint Metrics During Pedaling. IEEE Access 2020, 8, 122782–122790. [Google Scholar] [CrossRef]
- Ceseracciu, E.; Sawacha, Z.; Cobelli, C. Comparison of Markerless and Marker-Based Motion Capture Technologies through Simultaneous Data Collection during Gait: Proof of Concept. PLoS ONE 2014, 9, e87640. [Google Scholar] [CrossRef]
- Fisch, M.; Clark, R. Orientation Keypoints for 6D Human Pose Estimation. arXiv 2020, arXiv:2009.04930. [Google Scholar]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. ACM Trans. Graph. 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Mehta, D.; Sotnychenko, O.; Mueller, F.; Xu, W.; Elgharib, M.; Fua, P.; Seidel, H.-P.; Rhodin, H.; Pons-Moll, G.; Theobalt, C. XNect: Real-Time Multi-Person 3D Motion Capture with a Single RGB Camera. ACM Trans. Graph. 2020, 39, 82:1–82:17. [Google Scholar] [CrossRef]
- Rempe, D.; Guibas, L.J.; Hertzmann, A.; Russell, B.; Villegas, R.; Yang, J. Contact and Human Dynamics from Monocular Video. In Computer Vision—ECCV 2020; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Li, Z.; Sedlar, J.; Carpentier, J.; Laptev, I.; Mansard, N.; Sivic, J. Estimating 3D Motion and Forces of Person-Object Interactions From Monocular Video. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8632–8641. [Google Scholar]
- Rempe, D.; Birdal, T.; Hertzmann, A.; Yang, J.; Sridhar, S.; Guibas, L.J. HuMoR: 3D Human Motion Model for Robust Pose Estimation. arXiv 2021, arXiv:2105.04668. [Google Scholar]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating Musculoskeletal Dynamics and Neuromuscular Control to Study Human and Animal Movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef]
- Haralabidis, N.; Saxby, D.J.; Pizzolato, C.; Needham, L.; Cazzola, D.; Minahan, C. Fusing Accelerometry with Videography to Monitor the Effect of Fatigue on Punching Performance in Elite Boxers. Sensors 2020, 20, 5749. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Mikami, D.; Isogawa, M.; Kimata, H. Human Pose as Calibration Pattern: 3D Human Pose Estimation with Multiple Unsynchronized and Uncalibrated Cameras. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1856–18567. [Google Scholar]
- Ershadi-Nasab, S.; Kasaei, S.; Sanaei, E. Uncalibrated Multi-View Multiple Humans Association and 3D Pose Estimation by Adversarial Learning. Multimed. Tools Appl. 2021, 80, 2461–2488. [Google Scholar] [CrossRef]
- Dong, J.; Shuai, Q.; Zhang, Y.; Liu, X.; Zhou, X.; Bao, H. Motion Capture from Internet Videos. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12347, pp. 210–227. ISBN 978-3-030-58535-8. [Google Scholar]
- Hartley, R.I.; Sturm, P. Triangulation. Comput. Vis. Image Underst. 1997, 68, 146–157. [Google Scholar] [CrossRef]
- Miller, N.R.; Shapiro, R.; McLaughlin, T.M. A Technique for Obtaining Spatial Kinematic Parameters of Segments of Biomechanical Systems from Cinematographic Data. J. Biomech. 1980, 13, 535–547. [Google Scholar] [CrossRef]
- Labuguen, R.T.; Ingco, W.E.M.; Negrete, S.B.; Kogami, T.; Shibata, T. Performance Evaluation of Markerless 3D Skeleton Pose Estimates with Pop Dance Motion Sequence. In Proceedings of the 2020 Joint 9th International Conference on Informatics, Electronics & Vision (ICIEV) and 2020 4th International Conference on Imaging, Vision & Pattern Recognition (icIVPR), Kitakyushu, Japan, 26–29 August 2020. [Google Scholar]
- Nakano, N.; Sakura, T.; Ueda, K.; Omura, L.; Kimura, A.; Iino, Y.; Fukashiro, S.; Yoshioka, S. Evaluation of 3D Markerless Motion Capture Accuracy Using OpenPose with Multiple Video Cameras. Front. Sports Act. Living 2019. [Google Scholar] [CrossRef]
- Slembrouck, M.; Luong, H.; Gerlo, J.; Schütte, K.; Van Cauwelaert, D.; De Clercq, D.; Vanwanseele, B.; Veelaert, P.; Philips, W. Multiview 3D Markerless Human Pose Estimation from OpenPose Skeletons. In Advanced Concepts for Intelligent Vision Systems; Blanc-Talon, J., Delmas, P., Philips, W., Popescu, D., Scheunders, P., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12002, pp. 166–178. ISBN 978-3-030-40604-2. [Google Scholar]
- Bridgeman, L.; Volino, M.; Guillemaut, J.-Y.; Hilton, A. Multi-Person 3D Pose Estimation and Tracking in Sports. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; pp. 2487–2496. [Google Scholar]
- Chu, H.; Lee, J.-H.; Lee, Y.-C.; Hsu, C.-H.; Li, J.-D.; Chen, C.-S. Part-Aware Measurement for Robust Multi-View Multi-Human 3D Pose Estimation and Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Dong, J.; Jiang, W.; Huang, Q.; Bao, H.; Zhou, X. Fast and Robust Multi-Person 3D Pose Estimation From Multiple Views. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7784–7793. [Google Scholar]
- He, Y.; Yan, R.; Fragkiadaki, K.; Yu, S.-I. Epipolar Transformers. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 7776–7785. [Google Scholar]
- Iskakov, K.; Burkov, E.; Lempitsky, V.; Malkov, Y. Learnable Triangulation of Human Pose. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 7717–7726. [Google Scholar]
- Zago, M.; Luzzago, M.; Marangoni, T.; De Cecco, M.; Tarabini, M.; Galli, M. 3D Tracking of Human Motion Using Visual Skeletonization and Stereoscopic Vision. Front. Bioeng. Biotechnol. 2020, 8. [Google Scholar] [CrossRef]
- D’Antonio, E.; Taborri, J.; Mileti, I.; Rossi, S.; Patane, F. Validation of a 3D Markerless System for Gait Analysis Based on OpenPose and Two RGB Webcams. IEEE Sens. J. 2021, 21, 17064–17075. [Google Scholar] [CrossRef]
- Kanko, R.M.; Laende, E.; Selbie, W.S.; Deluzio, K.J. Inter-Session Repeatability of Markerless Motion Capture Gait Kinematics. J. Biomech. 2021, 121, 110422. [Google Scholar] [CrossRef] [PubMed]
- Kanko, R.M.; Laende, E.K.; Davis, E.M.; Scott Selbie, W.; Deluzio, K.J. Concurrent Assessment of Gait Kinematics Using Marker-Based and Markerless Motion Capture. J. Biomech. 2021, 127, 110665. [Google Scholar] [CrossRef]
- Karashchuk, P.; Rupp, K.L.; Dickinson, E.S.; Sanders, E.; Azim, E.; Brunton, B.W.; Tuthill, J.C. Anipose: A Toolkit for Robust Markerless 3D Pose Estimation. bioRxiv 2020. [Google Scholar] [CrossRef]
- Desmarais, Y.; Mottet, D.; Slangen, P.; Montesinos, P. A Review of 3D Human Pose Estimation Algorithms for Markerless Motion Capture. arXiv 2020, arXiv:2010.06449. [Google Scholar]
- Moeslund, T.B.; Granum, E. Review—A Survey of Computer Vision-Based Human Motion Capture. Comput. Vis. Image Underst. 2001, 81, 231–268. [Google Scholar] [CrossRef]
- Wang, J.; Jin, S.; Liu, W.; Liu, W.; Qian, C.; Luo, P. When Human Pose Estimation Meets Robustness: Adversarial Algorithms and Benchmarks. arXiv 2021, arXiv:2105.06152. [Google Scholar]
- Bala, P.C.; Eisenreich, B.R.; Yoo, S.B.M.; Hayden, B.Y.; Park, H.S.; Zimmermann, J. Automated Markerless Pose Estimation in Freely Moving Macaques with OpenMonkeyStudio. Nat. Commun. 2020, 11, 4560. [Google Scholar] [CrossRef]
- Sun, W.; Cooperstock, J.R. Requirements for Camera Calibration: Must Accuracy Come with a High Price? In Proceedings of the 2005 Seventh IEEE Workshops on Applications of Computer Vision (WACV/MOTION’05, Breckenridge, CO, USA, 5–7 January 2005; Volume 1, pp. 356–361. [Google Scholar]
- QTM User Manual. Available online: https://usermanual.wiki/buckets/85617/1437169750/QTM-user-manual.pdf (accessed on 21 September 2021).
- Dawson-Howe, K.M.; Vernon, D. Simple Pinhole Camera Calibration. Int. J. Imaging Syst. Technol. 1994, 5, 1–6. [Google Scholar] [CrossRef]
- Laurentini, A. The Visual Hull Concept for Silhouette-Based Image Understanding. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 150–162. [Google Scholar] [CrossRef]
- OpenPose Experimental Models. Available online: https://github.com/CMU-Perceptual-Computing-Lab/openpose_train (accessed on 21 July 2021).
- Zeni, J.A.; Richards, J.G.; Higginson, J.S. Two Simple Methods for Determining Gait Events during Treadmill and Overground Walking Using Kinematic Data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rajagopal, A.; Dembia, C.L.; DeMers, M.S.; Delp, D.D.; Hicks, J.L.; Delp, S.L. Full-Body Musculoskeletal Model for Muscle-Driven Simulation of Human Gait. IEEE Trans. Biomed. Eng. 2016, 63, 2068–2079. [Google Scholar] [CrossRef] [PubMed]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. A Public Dataset of Overground and Treadmill Walking Kinematics and Kinetics in Healthy Individuals. PeerJ 2018, 6, e4640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trinler, U.; Schwameder, H.; Baker, R.; Alexander, N. Muscle Force Estimation in Clinical Gait Analysis Using AnyBody and OpenSim. J. Biomech. 2019, 86, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.G.; Dingwell, J.B. Separating the Effects of Age and Walking Speed on Gait Variability. Gait Posture 2008, 27, 572–577. [Google Scholar] [CrossRef]
- Warmenhoven, J.; Harrison, A.; Robinson, M.A.; Vanrenterghem, J.; Bargary, N.; Smith, R.; Cobley, S.; Draper, C.; Donnelly, C.; Pataky, T. A Force Profile Analysis Comparison between Functional Data Analysis, Statistical Parametric Mapping and Statistical Non-Parametric Mapping in on-Water Single Sculling. J. Sci. Med. Sport 2018, 21, 1100–1105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Beaucage-Gauvreau, E.; Robertson, W.S.P.; Brandon, S.C.E.; Fraser, R.; Freeman, B.J.C.; Graham, R.B.; Thewlis, D.; Jones, C.F. Validation of an OpenSim Full-Body Model with Detailed Lumbar Spine for Estimating Lower Lumbar Spine Loads during Symmetric and Asymmetric Lifting Tasks. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 451–464. [Google Scholar] [CrossRef]
- Varol, G.; Romero, J.; Martin, X.; Mahmood, N.; Black, M.J.; Laptev, I.; Schmid, C. Learning from Synthetic Humans. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4627–4635. [Google Scholar]
- Bruno, A.G.; Bouxsein, M.L.; Anderson, D.E. Development and Validation of a Musculoskeletal Model of the Fully Articulated Thoracolumbar Spine and Rib Cage. J. Biomech. Eng. 2015, 137, 081003. [Google Scholar] [CrossRef]









| Tasks | Conditions | Mean Number of Excluded Cameras | Mean Absolute Reprojection Error | ||||
|---|---|---|---|---|---|---|---|
| Mean | std | Max | Mean | std | Max | ||
| Walking | Ref | 0.47 | 0.57 | 2.0 (Nose) | 3.3 px (1.6 cm) | 1.1 px (0.54 cm) | 5.3 px (2.6 cm, LHip) |
| Im | 0.91 | 0.80 | 2.4 (LWrist) | 3.7 px (1.8 cm) | 1.0 px (0.52 cm) | 5.2 px (2.6 cm, LSmallToe) | |
| 4c | 0.27 | 0.34 | 1.0 (Nose) | 2.9 px (1.4 cm) | 0.93 px (0.47 cm) | 4.5 px (2.2 cm, LSmallToe) | |
| Cal | 0.47 | 0.57 | 2.0 (Nose) | 5.1 px (2.5 cm) | 0.91 px (0.45 cm) | 6.9 px (3.4 cm, LHip) | |
| Running | Ref | 0.48 | 0.64 | 2.2 (LWrist) | 3.5 px (1.7 cm) | 1.2 px (0.57 cm) | 5.6 px (2.8 cm, LWrist) |
| Im | 0.94 | 1.2 | 4.5 (LWrist) | 4.0 px (2.0 cm) | 1.4 px (0.69 cm) | 7.2 px (3.6 cm, RWrist) | |
| 4c | 0.22 | 0.31 | 1.0 (LWrist) | 3.3 px (1.6 cm) | 0.97 px (0.48 cm) | 4.7 px (2.3 cm, LWrist) | |
| Cal | 0.47 | 0.65 | 2.2 (LWrist) | 5.4 px (2.7 cm) | 1.0 px (0.52 cm) | 7.2 px (3.6 cm, LWrist) | |
| Cycling | Ref | 1.62 | 1.4 | 4.2 (RBigToe) | 6.1 px (3.0 cm) | 1.2 px (0.58 cm) | 8.5 px (4.2 cm, Head) |
| Im | 2.41 | 1.9 | 5.7 (RBigToe) | 6.3 px (3.1 cm) | 1.3 px (0.60 cm) | 8.5 px (4.2 cm, Head) | |
| 4c | 0.76 | 0.67 | 2.1 (RBigToe) | 5.3 px (2.6 cm) | 1.6 px (0.82 cm) | 8.4 px (4.2 cm, LElbow) | |
| Cal | 1.68 | 1.4 | 4.24 (RBigToe) | 6.9 px (3.4 cm) | 1.0 px (0.51 cm) | 8.9 px (4.4 cm, Head) | |
| Tasks | Conditions | RMS Marker Error | ||
|---|---|---|---|---|
| Mean | std | Max | ||
| Walking | Ref | 2.8 cm | 0.13 cm | 3.2 cm (Mid stance) |
| Im | 2.8 cm | 0.11 cm | 3.1 cm (Mid stance) | |
| 4c | 2.8 cm | 0.12 cm | 3.2 cm (Mid stance) | |
| Cal | 2.9 cm | 0.13 cm | 3.2 cm (Mid stance) | |
| Running | Ref | 2.2 cm | 0.22 cm | 2.6 cm (Mid stance) |
| Im | 2.4 cm | 0.21 cm | 2.8 cm (Mid stance) | |
| 4c | 2.5 cm | 0.30 cm | 2.4 cm (Mid stance) | |
| Cal | 2.2 cm | 0.21 cm | 2.6 cm (Mid stance) | |
| Cycling | Ref | 3.4 cm | 0.11 cm | 3.6 cm (Dead center) |
| Im | 3.8 cm | 0.18 cm | 4.2 cm (Dead center) | |
| 4c | 3.9 cm | 0.60 cm | 5.9 cm (Dead center) | |
| Cal | 3.4 cm | 0.11 cm | 3.6 cm (Dead center) | |
| Task | Conditions | std (°) | std/stdref | r | MAE (°) |
|---|---|---|---|---|---|
| Walking | Ref | 2.56 | - | - | - |
| Im | 3.03 | 1.19 | 0.97 | 1.55 | |
| 4c | 3.24 | 1.27 | 0.97 | 1.50 | |
| Cal | 2.60 | 1.02 | 1.00 | 0.35 | |
| Running | Ref | 2.59 | - | - | - |
| Im | 2.76 | 1.07 | 0.99 | 0.92 | |
| 4c | 2.79 | 1.10 | 0.97 | 1.60 | |
| Cal | 2.54 | 0.98 | 1.00 | 0.47 | |
| Cycling | Ref | 1.78 | - | - | - |
| Im | 1.89 | 1.08 | 0.88 | 1.72 | |
| 4c | 3.04 | 1.93 | 0.81 | 1.54 | |
| Cal | 1.80 | 1.02 | 0.99 | 0.50 | |
| Cycling (lower-body only) | Ref | 2.09 | - | - | - |
| Im | 2.41 | 1.22 | 0.94 | 1.69 | |
| 4c | 3.82 | 2.31 | 0.90 | 1.84 | |
| Cal | 2.13 | 1.03 | 0.99 | 0.51 |
| Joint | Method | Flexion/Extension | Abduction/Adduction * | Internal/External Rotation |
|---|---|---|---|---|
| Ankle | Kang et al. [72] | 2 | 2.5 | - |
| Ours | 2.07 | 4.84 | - | |
| Knee | Kang et al. [72] | 0.7 | - | - |
| Ours | 4.85 | - | - | |
| Hip | Kang et al. [72] | 1.2 | 1.8 | 1.1 |
| Ours | 2.61 | 1.5 | 3.72 |
| Flexion/Extension | Abduction/Adduction * | Internal/External Rotation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| std/stdref | r | MAE (°) | std/stdref | r | MAE (°) | std/stdref | r | MAE (°) | ||
| Walking | Im | 1.11 | 1.00 | 1.48 | 1.28 | 0.98 | 1.05 | 1.23 | 0.89 | 2.47 |
| 4c | 1.15 | 1.00 | 0.90 | 1.29 | 0.93 | 1.28 | 1.54 | 0.94 | 3.35 | |
| Cal | 1.01 | 1.00 | 0.19 | 1.04 | 0.99 | 0.50 | 1.04 | 0.99 | 0.54 | |
| Running | Im | 1.03 | 1.00 | 0.98 | 1.08 | 0.98 | 0.48 | 1.13 | 0.98 | 1.41 |
| 4c | 1.03 | 1.00 | 0.98 | 1.18 | 0.93 | 1.00 | 1.14 | 0.97 | 4.06 | |
| Cal | 1.00 | 1.00 | 0.30 | 0.99 | 0.99 | 0.53 | 0.92 | 1.00 | 0.80 | |
| Cycling | Im | 0.99 | 0.97 | 1.89 | 1.27 | 0.66 | 1.45 | 0.99 | 0.97 | 1.71 |
| 4c | 1.31 | 0.96 | 1.43 | 3.10 | 0.46 | 1.76 | 1.71 | 0.97 | 1.47 | |
| Cal | 1.00 | 1.00 | 0.39 | 1.06 | 0.96 | 0.36 | 1.02 | 1.00 | 1.00 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pagnon, D.; Domalain, M.; Reveret, L. Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness. Sensors 2021, 21, 6530. https://doi.org/10.3390/s21196530
Pagnon D, Domalain M, Reveret L. Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness. Sensors. 2021; 21(19):6530. https://doi.org/10.3390/s21196530
Chicago/Turabian StylePagnon, David, Mathieu Domalain, and Lionel Reveret. 2021. "Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness" Sensors 21, no. 19: 6530. https://doi.org/10.3390/s21196530
APA StylePagnon, D., Domalain, M., & Reveret, L. (2021). Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness. Sensors, 21(19), 6530. https://doi.org/10.3390/s21196530