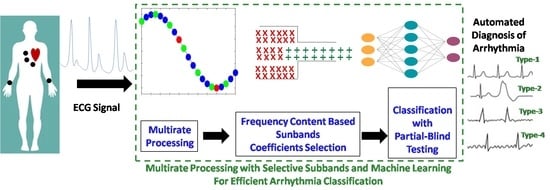
Multirate Processing with Selective Subbands and Machine Learning for Efficient Arrhythmia Classification †
Abstract
:1. Introduction
- (i).
- Multirate processing is used for computationally efficient system realization.
- (ii).
- QRS selection is used to focus on the relevant signal part while avoiding the unwanted baseline. It also enhances the system computational effectiveness.
- (iii).
- Each selected QRS segment is filtered by using a multirate lower-taps FIR filter.
- (iv).
- An effective wavelet decomposition scheme is proposed for subband extraction.
- (v).
- A frequency content-dependent subband coefficient selection is performed to attain the dimension reduction.
- (vi).
- The performance of KNN, ANN, SVM, RF, decision tree (DT) and bagging (BG) is studied for the automated recognition of arrhythmia by using the forehand selected features.
- (vii).
- To avoid over fitting and any biasness, the classification performance is evaluated by using the 5CV and a novel partial blind testing protocol.
2. Materials and Methods
2.1. Dataset
2.2. Decimation with QRS Selection and Denoising
2.3. Wavelet Decomoposition
2.4. Subband Coefficient Selection
2.5. Classification Methods
2.5.1. Artificial Neural Network (ANN)
2.5.2. k-Nearest Neighbours (k-NN)
2.5.3. Decision Tree (DT)
2.5.4. Support Vector Machine (SVM)
2.5.5. Random Forest (RF)
2.5.6. Bagging (BG)
2.6. Performance Evaluation Metrics
2.6.1. Compression Ratio
2.6.2. Computational Complexity
2.6.3. Reconstruction Error
2.6.4. Classification Evaluation
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Ethical Approval
Acknowledgments
Conflicts of Interest
References
- Benjamin, E.J.; Muntner, P.; Alonso, A.; Bittencourt, M.S.; Callaway, C.W.; Carson, A.P.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Das, S.R.; et al. Heart disease and stroke Statistics-2019 update a report from the American Heart Association. Circulation 2019, 139, e56–e528. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Mitra, M. Application of Cross Wavelet Transform for ECG Pattern Analysis and Classification. IEEE Trans. Instrum. Meas. 2014, 63, 326–333. [Google Scholar] [CrossRef]
- Nascimento, N.M.M.; Marinho, L.B.; Peixoto, S.A.; Madeiro, J.P.D.V.; De Albuquerque, V.H.C.; Filho, P.P.R. Heart Arrhythmia Classification Based on Statistical Moments and Structural Co-occurrence. Circuits Syst. Signal Process. 2019, 39, 631–650. [Google Scholar] [CrossRef]
- Mazaheri, V.; Khodadadi, H. Heart arrhythmia diagnosis based on the combination of morphological, frequency and nonlinear features of ECG signals and metaheuristic feature selection algorithm. Expert Syst. Appl. 2020, 161, 113697. [Google Scholar] [CrossRef]
- Qaisar, S.M.; Krichen, M.; Jallouli, F. Multirate ECG Processing and k-Nearest Neighbor Classifier Based Efficient Arrhythmia Diagnosis. In Proceedings of the Lecture Notes in Computer Science, Constructive Side-Channel Analysis and Secure Design, Hammamet, Tunisia, 24–26 June 2020; Springer: Cham, Switzerland, 2020; pp. 329–337. [Google Scholar]
- Qaisar, S.M.; Subasi, A. Cloud-based ECG monitoring using event-driven ECG acquisition and machine learning techniques. Phys. Eng. Sci. Med. 2020, 43, 623–634. [Google Scholar] [CrossRef]
- Qaisar, S.M.; Hussain, S.F. Arrhythmia Diagnosis by Using Level-Crossing ECG Sampling and Sub-Bands Features Extraction for Mobile Healthcare. Sensors 2020, 20, 2252. [Google Scholar] [CrossRef] [Green Version]
- Qaisar, S.M. Baseline wander and power-line interference elimination of ECG signals using efficient signal-piloted filtering. Heal. Technol. Lett. 2020, 7, 114–118. [Google Scholar] [CrossRef]
- Sharma, R.R.; Pachori, R.B. Baseline wander and power line interference removal from ECG signals using eigenvalue decomposition. Biomed. Signal Process. Control 2018, 45, 33–49. [Google Scholar] [CrossRef]
- Hesar, H.D.; Mohebbi, M. An Adaptive Particle Weighting Strategy for ECG Denoising Using Marginalized Particle Extended Kalman Filter: An Evaluation in Arrhythmia Contexts. IEEE J. Biomed. Health Inform. 2017, 21, 1581–1592. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Zhang, L.; Wu, H.-T. A Novel Blaschke Unwinding Adaptive-Fourier-Decomposition-Based Signal Compression Algorithm With Application on ECG Signals. IEEE J. Biomed. Health Inform. 2018, 23, 672–682. [Google Scholar] [CrossRef]
- Jha, C.K.; Kolekar, M.H. Cardiac arrhythmia classification using tunable Q-wavelet transform based features and support vector machine classifier. Biomed. Signal Process. Control 2020, 59, 101875. [Google Scholar] [CrossRef]
- Hai, N.T.; Nguyen, N.T.; Nguyen, M.H.; Livatino, S. Wavelet-Based Kernel Construction for Heart Disease Classification. Adv. Electr. Electron. Eng. 2019, 17, 306–319. [Google Scholar] [CrossRef]
- Sharma, M.; Tan, R.-S.; Acharya, U.R. Automated heartbeat classification and detection of arrhythmia using optimal orthogonal wavelet filters. Inform. Med. Unlocked 2019, 16, 100221. [Google Scholar] [CrossRef]
- Li, T.; Zhou, M. ECG Classification Using Wavelet Packet Entropy and Random Forests. Entropy 2016, 18, 285. [Google Scholar] [CrossRef]
- Gutiérrez-Gnecchi, J.A.; Morfin-Magaña, R.; Lorias-Espinoza, D.; Tellez-Anguiano, A.D.C.; Reyes-Archundia, E.; Méndez-Patiño, A.; Castañeda-Miranda, R. DSP-based arrhythmia classification using wavelet transform and probabilistic neural network. Biomed. Signal Process. Control 2017, 32, 44–56. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Chen, B.; Yao, B.; He, W. ECG Arrhythmia Classification Using STFT-Based Spectrogram and Convolutional Neural Network. IEEE Access 2019, 7, 92871–92880. [Google Scholar] [CrossRef]
- Berraih, S.A.; Baakek, Y.N.E.; Debbal, S.M.E.A. Pathological discrimination of the phonocardiogram signal using the bispectral technique. Phys. Eng. Sci. Med. 2020, 43, 1371–1385. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.; Mohanty, M.; Sabut, S. Automated ECG beat classification using DWT and Hilbert transform-based PCA-SVM classifier. Int. J. Biomed. Eng. Technol. 2020, 32, 287–303. [Google Scholar] [CrossRef]
- Majumder, S.; Chen, L.; Marinov, O.; Chen, C.-H.; Mondal, T.; Deen, M.J. Noncontact Wearable Wireless ECG Systems for Long-Term Monitoring. IEEE Rev. Biomed. Eng. 2018, 11, 306–321. [Google Scholar] [CrossRef]
- Deepu, C.J.; Zhang, X.; Heng, C.H.; Lian, Y. A 3-Lead ECG-on-Chip with QRS Detection and Lossless Compression for Wireless Sensors. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 1151–1155. [Google Scholar] [CrossRef]
- Sahoo, S.; Kanungo, B.; Behera, S.; Sabut, S. Multiresolution wavelet transform based feature extraction and ECG classification to detect cardiac abnormalities. Measurement 2017, 108, 55–66. [Google Scholar] [CrossRef]
- Yildirim, Ö. A novel wavelet sequence based on deep bidirectional LSTM network model for ECG signal classification. Comput. Biol. Med. 2018, 96, 189–202. [Google Scholar] [CrossRef]
- Hou, B.; Yang, J.; Wang, P.; Yan, R. LSTM-Based Auto-Encoder Model for ECG Arrhythmias Classification. IEEE Trans. Instrum. Meas. 2020, 69, 1232–1240. [Google Scholar] [CrossRef]
- Anwar, S.M.; Gul, M.; Majid, M.; Alnowami, M. Arrhythmia Classification of ECG Signals Using Hybrid Features. Comput. Math. Methods Med. 2018, 2018, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Zhou, Q.; Lei, L.; Zheng, K.; Xiang, W. An IoT-cloud based wearable ECG monitoring system for smart healthcare. J. Med Syst. 2016, 40, 286. [Google Scholar] [CrossRef]
- Jiang, Y.; Qi, Y.; Wang, W.K.; Bent, B.; Avram, R.; Olgin, J.; Dunn, J. EventDTW: An Improved Dynamic Time Warping Algorithm for Aligning Biomedical Signals of Nonuniform Sampling Frequencies. Sensors 2020, 20, 2700. [Google Scholar] [CrossRef]
- Moody, G.; Mark, R. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Boil. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- The Database of Multichannel ECG Recordings with Heartbeats Annotated by Cardiologists. Available online: https://physionet.org/content/mitdb/1.0.0/ (accessed on 1 January 2021).
- Antoniou, A. Digital Signal Processing; McGraw-Hill: New York, NY, USA, 2016. [Google Scholar]
- Liu, C.; Zhang, X.; Zhao, L.; Liu, F.; Chen, X.; Yao, Y.; Li, J. Signal Quality Assessment and Lightweight QRS Detection for Wearable ECG SmartVest System. IEEE Internet Things J. 2019, 6, 1363–1374. [Google Scholar] [CrossRef]
- Qaisar, S.M. Efficient mobile systems based on adaptive rate signal processing. Comput. Electr. Eng. 2019, 79, 106462. [Google Scholar] [CrossRef]
- Lin, C.-H. Frequency-domain features for ECG beat discrimination using grey relational analysis-based classifier. Comput. Math. Appl. 2008, 55, 680–690. [Google Scholar] [CrossRef] [Green Version]
- Van Gerven, M.; Bohte, S. Editorial: Artificial Neural Networks as Models of Neural Information Processing. Front. Comput. Neurosci. 2017, 11, 114. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Xu, H.; Liu, X.; Lu, S. Emotion recognition from multichannel EEG signals using K-nearest neighbor classification. Technol. Health Care 2018, 26, 509–519. [Google Scholar] [CrossRef]
- Grąbczewski, K. Techniques of Decision Tree Induction. In Complex Networks & Their Applications IX; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; Volume 498, pp. 11–117. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Kulisch, U.W.; Miranker, W.L. Computer Arithmetic in Theory and Practice; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Chen, C.; Hua, Z.; Zhang, R.; Liu, G.; Wen, W. Automated arrhythmia classification based on a combination network of CNN and LSTM. Biomed. Signal Process. Control 2020, 57, 101819. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Elsevier Morgan Kaufmann: San Francisco, CA, USA, 2011. [Google Scholar]
- Zhang, Z.; Telesford, Q.K.; Giusti, C.; Lim, K.O.; Bassett, D.S. Choosing Wavelet Methods, Filters, and Lengths for Functional Brain Network Construction. PLoS ONE 2016, 11, e0157243. [Google Scholar] [CrossRef]









| Class | MSE1 ×(10−6) V2 | MSE2 ×(10−6) V2 | For All Classes MSE1 ×(10−6)V2 | For All Classes MSE2 ×(10−6)V2 |
|---|---|---|---|---|
| N | 6.837 | 2.173 | 32.514 | 1.256 |
| RBBB | 82.765 | 1.832 | ||
| APC | 25.691 | 0.202 | ||
| LBBB | 14.762 | 0.816 |
| Accuracy | ||||
|---|---|---|---|---|
| Protocol | 5CV | Partial Blind | ||
| Classifier/Dataset | P1 | P2 | P1 | P2 |
| ANN | 96.62 (±0.81) | 95.83 (±1.18) | 91.60 (±3.14) | 92.08 (±2.30) |
| KNN | 96.37 (±0.57) | 96.27 (±0.42) | 91.32 (±2.35) | 90.07 (±2.15) |
| DT | 95.34 (±0.79) | 93.92 (±0.95) | 87.08 (±4.34) | 85.00 (±4.09) |
| SVM | 96.76 (±0.84) | 97.06 (±0.89) | 91.67 (±1.48) | 90.62 (±2.67) |
| RF | 97.35 (±0.72) | 96.91 (±0.50) | 92.99 (±1.39) | 91.60 (±0.20) |
| BAG | 96.96 (±0.92) | 96.52 (±1.32) | 90.00 (±3.58) | 90.35 (±1.75) |
| Kappa | ||||
|---|---|---|---|---|
| Protocol | 5CV | Partial Blind | ||
| Classifier/Dataset | P1 | P2 | P1 | P2 |
| ANN | 95.48 (±1.08) | 94.43 (±1.58) | 88.80 (±4.18) | 89.44 (±3.07) |
| KNN | 95.16 (±0.76) | 95.03 (±0.56) | 88.43 (±3.13) | 86.76 (±2.87) |
| DT | 93.78 (±1.05) | 91.89 (±1.27) | 82.78 (±5.79) | 80.00 (±5.46) |
| SVM | 95.68 (±1.12) | 96.07 (±1.19) | 88.89 (±1.98) | 87.50 (±3.56) |
| RF | 96.47 (±0.96) | 95.88 (±0.68) | 90.65 (±1.85) | 88.80 (±0.26) |
| BAG | 95.94 (±1.24) | 95.35 (±1.76) | 86.67 (±4.78) | 87.13 (±2.33) |
| AUC | ||||
|---|---|---|---|---|
| Protocol | 5CV | Partial Blind | ||
| Classifier/Dataset | P1 | P2 | P1 | P2 |
| ANN | 99.67 (±0.15) | 99.50 (±0.19) | 98.83 (±0.66) | 97.90 (±0.47) |
| KNN | 99.37 (±0.22) | 99.21 (±0.37) | 98.30 (±0.47) | 97.78 (±0.66) |
| DT | 96.90 (±0.55) | 95.99 (±0.60) | 91.39 (±2.90) | 90.00 (±2.73) |
| SVM | 99.55 (±0.23) | 99.49 (±0.26) | 98.88 (±0.35) | 97.62 (±0.58) |
| RF | 99.86 (±0.08) | 99.77 (±0.10) | 99.51 (±0.24) | 98.84 (±0.17) |
| BAG | 99.79 (±0.09) | 99.69 (±0.16) | 99.15 (±0.55) | 98.33 (±0.29) |
| Predicted | |||||
|---|---|---|---|---|---|
| N | RBBB | APC | LBBB | ||
| Actual | N | 498 | 1 | 4 | 7 |
| RBBB | 3 | 501 | 0 | 6 | |
| APC | 24 | 1 | 481 | 4 | |
| LBBB | 3 | 0 | 1 | 506 | |
| Predicted | |||||
|---|---|---|---|---|---|
| N | RBBB | APC | LBBB | ||
| Actual | N | 494 | 1 | 10 | 5 |
| RBBB | 2 | 504 | 0 | 4 | |
| APC | 22 | 3 | 482 | 3 | |
| LBBB | 5 | 2 | 3 | 500 | |
| Predicted | |||||
|---|---|---|---|---|---|
| N | RBBB | APC | LBBB | ||
| Actual | N | 333 | 3 | 21 | 3 |
| RBBB | 9 | 332 | 14 | 5 | |
| APC | 26 | 1 | 327 | 6 | |
| LBBB | 1 | 0 | 12 | 347 | |
| Predicted | |||||
|---|---|---|---|---|---|
| N | RBBB | APC | LBBB | ||
| Actual | N | 315 | 4 | 40 | 1 |
| RBBB | 7 | 338 | 10 | 5 | |
| APC | 28 | 0 | 328 | 4 | |
| LBBB | 1 | 9 | 5 | 345 | |
| Study | Features Extraction | Classification Method | No. of Classes | Accuracy (%) |
|---|---|---|---|---|
| [12] | Tunable Q-wavelet Transform (TQWT) | SVM (36% training-64% testing split, without blind testing) | 8 | 99.27 |
| [14] | DWT + Fuzzy and Renyi Entropy + Fractal Dimension | KNN (CV) | 5 | 98.1 |
| [15] | Wavelet Packet Entropy (WPE) | RF (Inter-Patient Scheme with CV) | 5 | 94.61 |
| [16] | Discrete Wavelet Transform (DWT) | Probabilistic Neural Network (PNN) (50% training-50% testing split, without blind testing) | 8 | 92.75 |
| [17] | Short Time Fourier Transform (STFT) | Convolutional Neural Network (CNN) (80%training-20%testing split, without blind testing) | 5 | 99.0 |
| [22] | DWT + Temporal + Morphological | SVM (CV) | 4 | 98.4 |
| [23] | DWT | Long Short Term Memory (LSTM) (60% training-20% validation-20% testing split, without blind testing) | 5 | 99.4 |
| [24] | LSTM-based auto-encoder (AE) network | SVM (CV) | 5 | 99.45 |
| [25] | DWT + RR Interval + Teager Energy Operator | ANN (CV) | 5 | 99.75 |
| This Study | Specific Wavelet Decomposition Scheme + Content based subbands selection, [] | ANN (Partial Blind) | 4 | 92.09 |
| Specific Wavelet Decomposition Scheme + Content based subbands selection, [] | SVM (5CV) | 4 | 97.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qaisar, S.M.; Mihoub, A.; Krichen, M.; Nisar, H. Multirate Processing with Selective Subbands and Machine Learning for Efficient Arrhythmia Classification. Sensors 2021, 21, 1511. https://doi.org/10.3390/s21041511
Qaisar SM, Mihoub A, Krichen M, Nisar H. Multirate Processing with Selective Subbands and Machine Learning for Efficient Arrhythmia Classification. Sensors. 2021; 21(4):1511. https://doi.org/10.3390/s21041511
Chicago/Turabian StyleQaisar, Saeed Mian, Alaeddine Mihoub, Moez Krichen, and Humaira Nisar. 2021. "Multirate Processing with Selective Subbands and Machine Learning for Efficient Arrhythmia Classification" Sensors 21, no. 4: 1511. https://doi.org/10.3390/s21041511
APA StyleQaisar, S. M., Mihoub, A., Krichen, M., & Nisar, H. (2021). Multirate Processing with Selective Subbands and Machine Learning for Efficient Arrhythmia Classification. Sensors, 21(4), 1511. https://doi.org/10.3390/s21041511