Evaluating the Heterogeneity Effect of Fertilizer Use Intensity on Agricultural Eco-Efficiency in China: Evidence from a Panel Quantile Regression Model
Abstract
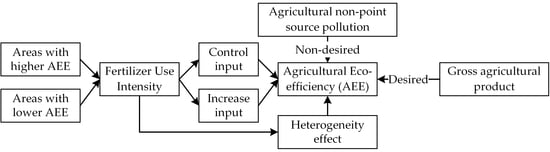
:1. Introduction
2. Theoretical Basis and Literature Review
3. Materials and Methods
3.1. Super-Efficient SBM Model
3.2. Baseline Model and Variable Selection
- (i).
- Rural labor transfer (RLT) = rural employees-agricultural employees. The difficult data acquisition of provincial rural transfer from existing statistics means this paper can only define it from an employment standpoint. The rural labor transfer direction from the agricultural to the non-agricultural realm coincides with its changed number [15]. The index explanation part of the China Statistical Yearbook shows that rural employees are divided into agriculture, industry, construction, and other fields. According to the longest time engaged in the main sector (the same time according to income). The real situation of rural employees in the non-agricultural industries agrees with the definition in this paper.
- (ii).
- Disposable income of rural households per capita (DIR). The affluence of rural households that represent the basis for agricultural production and management can influence the scale and structure of agricultural input factors affecting AEE characterized by the per capita disposable income of rural households.
- (iii).
- Machinery input intensity (MII) = total power of agricultural machinery/per unit sown area. At present, China’s agricultural production techniques have completed the transformation from relying mainly on human and animal power to relying mainly on mechanical power. Machinery use, the most intuitive manifestation of the agricultural technology progress, can improve agricultural output by popularizing machinery services and promoting labor productivity by effectively replacing the labor force.
- (iv).
- Multiple crop index (MCI) = total crop sown area/cropland area. Multiple crop index, the average number of crops planted on the same cultivated land in a certain period (usually one year), is adopted to reflect the impact of changes in the degree of cultivated land use on AEE. The proportion of sown area to cropland area is usually used to characterize the MCI, where the sown area is similar to the gross cropped area and cultivated land area is similar to the net cropped area.
- (v).
- Crop planting structure (CPS) = grain crop planting area/total crop sown area. Planting structure refers to the proportion of crop types grown in a certain area with its change leading to the changed agricultural input factor structure, affecting AEE.
- (vi).
- Fiscal supporting on agriculture (FSA) = fiscal expenditure on agriculture, forestry, and water affairs/total crop sown area. The subsidy intensity of financial funds to agriculture can affect the input of rural residents to agricultural resources such as chemical fertilizer, pesticides, and agricultural machinery services and can reflect the impact of the administrative intervention on AEE.
3.3. Quantile Regression Model
3.4. Data Sources
4. Results
4.1. Measurement of AEE
- (1)
- The interpretation of the trend reveals that the average AEE, which is essentially under 0.8 in most years, sees a low level of AEE with a stable upward trend in China. However, the years 1978–2000 saw volatility and fluctuation in AEE with a small increase magnitude, while from the year 2000 onwards it enjoyed a stable upward trend, before falling back after 2016.
- (2)
- The division into two stages with the year 2000 as the boundary in the context of comparing the AEE of the four major regions. The ranking of AEE during 1978–2000 is WR > ER > NER > CR, while during 2000–2018 is ER > WR > NER > CR, with a small gap between the CR and the WR, while after 2016, the change of AEE in the NER and CR is the opposite trend from the ER and WR, with the gap between regions first widening and then narrowing.
4.2. The Heterogeneity Impact of FUI on AEE
- (1)
- RLT has a inhibitory effect on the AEE, and this negative impact shows a persistent enhancement as the quantile rises, indicating that areas with a higher AEE are more negatively affected by rural labor transfer.
- (2)
- The increase of DIR helps improve AEE, which is similar to the findings of Xu et al. [59]. In addition, the positive impact of DIR increases with the increase of the quantile, indicating that areas with higher AEE are more positively affected by the DIR.
- (3)
- The coefficients of MII showed a shift from negative to positive at different quantile points, indicating that the negative effect of MII on the AEE gradually disappeared and the positive effect gradually appeared as the quantile points rose. However, the impact of MII was not significant at the low quantile (10%, 20%) and high quantile (90%), implying that areas with low and high AEE were not significantly affected by machinery inputs.
- (4)
- The coefficient changes of the MCI at different quantile points were similar to those of the MII, which also showed a shift from negative to positive, starting from the 30% quantile to be significantly positive, and reaching the maximum at the 80% quantile, indicating that the positive effect of the MCI gradually increased as the quantile point rose, and that the positive effect of the MCI was more prominent in areas with a high AEE.
- (5)
- The effect of CPS on the AEE was significantly negative at different quantile points, and this negative impact showed a continuous enhancement of transformation characteristics as the quantile point increased, reaching the highest at the 90% quantile, implying that the increase in the proportion of food crop cultivation is not conducive to enhancing AEE, and the areas with higher AEE are more negatively affected by the CPS.
- (6)
- The coefficients of FAS also showed a shift from negative to positive at different quartiles, with negative coefficients gradually insignificant and positive coefficients gradually significant; and the positive effect reached the highest point at the 90% quartile, indicating that FSA had a stronger positive promoting effect on the more efficient regions and a more negative inhibiting effect on the less efficient regions.
4.3. Spatial–Temporal Differences of FUI Impact
- (1)
- The coefficients in the ER undergo a similar U-shaped change from positive to negative, strengthening and then weakening, with the coefficient turning from positive to negative in 40~50% quantile, and the greatest positive impact at the 30% quantile and the strongest negative impact at the 90% quantile. This indicates that the FUI has a positive promoting effect on the lower AEE regions and a negative inhibiting effect on the more efficient regions in the ER, where the greater the quartile, the stronger the negative impact, which is inconsistent with the results at the national level and may be related to the differences in endowment conditions and the positioning of agricultural production within the ER.
- (2)
- The coefficients in the CR showed a transformation from “positive → negative → positive”, first weakening negatively and then strengthening positively, with a negative effect in 40~70% quartiles and a positive effect at both lower and higher quartiles. This indicates that FUI has a significant positive effect on both the lower and higher AEE areas in the CR, but does not have a significant negative effect on the areas with intermediate efficiency, probably because the provinces in the CR are mainly grain-producing areas with better agricultural production conditions, and fertilizer use tends to be dynamically balanced.
- (3)
- The coefficients in the WR showed a similar inverted U-shaped shift of rising and then falling, except for a weaker but insignificant negative effect at the 50~70% quantile, and the significantly negative effect at all other quantiles with larger negative inhibition at both the low and high quartiles. This indicates that FUI has a stronger negative inhibitory effect in the WR regions with lower and higher agroecological efficiency. This is closely related to the agricultural production conditions and endowment base in the WR, and for the WR regions with high efficiency, increasing FUI is more likely to break the equilibrium relationship between inputs and outputs.
- (4)
- The coefficients in the NER were all significantly negative and gradually strengthening, but the negative effect was more stable at both the low and high quartiles, indicating that FUI has a significant negative effect on areas in the NER at different efficiency levels, and the higher the AEE, the more pronounced the negative inhibitory effect of FUI.
- (1)
- The FUI coefficients during 1978–1989 show a negative to positive shift at different quartiles, with the negative effect weakening and positive effect increasing and starting to exert positive effect after the 60% quantile but only reaching significance at the high (80~90%) quantile, where fertilizer has a positive enhancing effect. This indicates that FUI had a negative inhibitory effect on areas with low AEE, and a positive promoting effect on areas with high AEE during this period.
- (2)
- The FUI coefficients during 1993–2003 were significantly negative at all quartiles, and this negative effect showed a first weakening and then strengthening shift, with a less negative effect of FUI on areas at the 40% to 60% quartiles; indicating that FUI had a strong negative inhibitory effect on both high and low AEE areas during this period.
- (3)
- The FUI coefficients during 2004–2020 showed a shift from positive to negative at each quantile, with the positive effect weakening and negative effect increasing, which is the opposite of the period 1978–1989, when FUI had a stronger negative effect on areas in the high quantile (80~90%).
4.4. Considering the Spatial Effect of Agricultural Production
5. Discussion
6. Conclusions
- (1)
- AEE of China shows a stable upward trend amidst fluctuations, remains at a low level overall, and there is more room for resource conservation and environmental protection, with significant inter-regional differences. Fluctuation in the AEE is mainly concentrated between 1978–2000, with a more pronounced increase in the eastern regions than in the mid-west and western regions during 2001–2020.
- (2)
- At different quantiles, the increase in FUI has a significant negative inhibitory effect on the improvement of AEE. The negative effect of FUI on AEE showed a gradual weakening and then a slight rebound shift as the quantile increased. FUI had a stronger negative effect at the lower quantile.
- (3)
- For different economic sub-divisions, FUI in the ER had a positive promoting effect on areas with lower AEE, FUI in the CR had a significant positive effect on areas of both lower and higher AEE, and FUI in the WR had a stronger negative inhibiting effect on areas of both lower and higher AEE, and FUI in the northeast region has a more pronounced negative inhibiting effect on areas of higher AEE. For different sub-periods, FUI positively promoted the areas with high AEE in 1978–1989, then FUI had a strong negative inhibitory effect on areas of both high and low AEE in 1993–2003, and FUI had a stronger negative effect on areas of high AEE in 2004–2020.
- (4)
- After considering the spatial lag of FUI, the negative effect of FUI undergoes a gradual decreasing transformation with the rise of quantile, and the decay of this negative effect was faster. Although FUI had a negative effect on local AEE, it had a positive spillover effect on the AEE of neighboring areas, and the higher the AEE, the stronger the positive spatial spillover effect of fertilizer use.
7. Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Wang, Z.; Xiao, H. Analysis of chemical fertilizer on the growth of grain output. Issues Agric. Econ. 2008, 8, 65–68. [Google Scholar]
- Yang, J.; Lin, Y. Spatiotemporal evolution and driving factors of fertilizer reduction control in Zhejiang Province. Sci. Total Environ. 2019, 660, 650–659. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Ma, J. Economic level of chemical fertilizer application in grain production of farm households: An example of wheat growers in the North China Plain. J. Agrotech. Econ. 2013, 1, 25–31. [Google Scholar] [CrossRef]
- Mueller, N.D.; West, P.C.; Gerber, J.S.; MacDonald, G.K.; Polasky, S.; Foley, J.A. A tradeoff frontier for global nitrogen use and cereal production. Environ. Res. Lett. 2014, 9, 054002. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.X.; Peng, H.; Jin, X.C. The effect of different stages of fertilizer application on grain yield in China—Based on panel data of 30 provinces from 1952–2006. J. Agrotech. Econ. 2008, 4, 85–94. [Google Scholar]
- Ge, J.H.; Zhou, S.D. Does factor market distortions stimulate the agricultural non-point source pollution? A case study of fertilizer. Issues Agric. Econ. 2012, 33, 92–100. [Google Scholar] [CrossRef]
- Fischer, G.; Winiwarter, W.; Ermolieva, T.; Cao, G.Y.; Qui, H.; Klimont, Z.; Wagner, F. Integrated Modeling Framework for Assessment and Mitigation of Nitrogen Pollution from Agriculture: Concept and Case Study for China. Agric. Ecosyst. Environ. 2010, 136, 116–124. [Google Scholar] [CrossRef]
- Guo, J.H.; Liu, X.J.; Zhang, Y.; Shen, J.L.; Han, W.X.; Zhang, W.F.; Zhang, F.S. Significant Acidification in Major Chinese Croplands. Science 2010, 327, 1008–1010. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.L.; Guo, Y.; Zhu, J.F. Evaluation of over fertilization in China and its influencing factors. Res. Agric. Mod. 2016, 37, 671–679. [Google Scholar] [CrossRef]
- Huang, J.K.; Hu, R.F.; Cao, J.M.; Rozelle, S. Training programs and in-the-field guidance to reduce China’s overuse of fertilizer without hurting profitability. J. Soil Water Conserv. 2008, 63, 165A–167A. [Google Scholar] [CrossRef]
- Suárez, R.P.; Goijman, A.P.; Cappelletti, S.; Solari, L.M.; Cristos, D.; Rojas, D.; Gavier-Pizarro, G.I. Combined effects of agrochemical contamination and forest loss on anuran diversity in agroecosystems of east-central Argentina. Sci. Total Environ. 2020, 759, 143435. [Google Scholar] [CrossRef] [PubMed]
- Hou, L.Y.; Liu, Z.J.; Zhao, J.R.; Ma, P.; Xu, X. Comprehensive assessment of fertilization, spatial variability of soil chemical properties, and relationships among nutrients, apple yield and orchard age: A case study in Luochuan County, China. Ecol. Indic. 2021, 122, 107285. [Google Scholar] [CrossRef]
- Grobelak, A.; Kokot, P.; Hutchison, D.; Grosser, A.; Kacprzak, A. Plant growth-promoting rhizobacteria as an alternative to mineral fertilizers in assisted bioremediation—Sustainable land and waste management. J. Environ. Manag. 2018, 227, 1–9. [Google Scholar] [CrossRef]
- Gorazda, K.; Tarko, B.; Wzorek, Z.; Kominko, H.; Nowak, A.K.; Kulczycka, J.; Smol, M. Fertilizers production from ashes after sewage sludge combustion—A strategy towards sustainable development. Environ. Res. 2017, 154, 171–180. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.L.; Li, Y.; Zhu, J.F. Rural labor transfer, excessive fertilizer use and agricultural non-point source pollution. J. China Agric. Univ. 2016, 21, 169–180. [Google Scholar] [CrossRef]
- Schaltegger, S.; Sturm, A. Okologische rationalitat. Die Unternehm. 1990, 44, 273–290. [Google Scholar]
- WBCSD. Eco-Efficient Leadership for Improved Economic and Environmental Performance; WBCSD: Geneva, Switzerland, 1996; pp. 3–16. [Google Scholar]
- OECD. Eco-Efficiency. Organization for Economic Cooperation and Development; OECD: Paris, France, 1998. [Google Scholar]
- Liu, Y.S.; Zou, L.L.; Wang, Y.S. Spatial-temporal characteristics and influencing factors of agricultural eco-efficiency in China in recent 40 years. Land Use Policy 2020, 97, 104794. [Google Scholar] [CrossRef]
- Pan, D.; Ying, R.Y. Agricultural eco-efficiency evaluation in China based on SBM model. Acta Ecol. Sin. 2013, 33, 3837–3845. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.H.; Song, S.F. Rural–urban migration and urbanization in China: Evidence from time-series and cross-section analyses. China Econ. Rev. 2003, 14, 386–400. [Google Scholar] [CrossRef]
- Hou, M.Y.; Deng, Y.J.; Yao, S.B. Spatial agglomeration pattern and driving factors of grain production in China since the Reform and Opening Up. Land 2021, 10, 10. [Google Scholar] [CrossRef]
- Zheng, H.Y.; Li, G.C. The impact of urban-rural biased policy on agricultural resource allocation efficiency. J. Agrotech. Econ. 2020, 07, 79–92. [Google Scholar] [CrossRef]
- Zhang, C.Q.; Wang, L.; Hua, C.L.; Jin, S.T.; Liu, P.T. Potentialities of fertilizer reduction for grain produce and effects on carbon emissions. Resour. Sci. 2016, 38, 790–797. [Google Scholar] [CrossRef]
- Guangbin, Z.; Kaifu, S.; Xi, M.; Qiong, H.; Jing, M.; Hua, G.; Hua, X. Nitrous oxide emissions, ammonia volatilization, and grain-heavy metal levels during the wheat season: Effect of partial organic substitution for chemical fertilizer. Agric. Ecosyst. Environ. 2021, 311, 107340. [Google Scholar] [CrossRef]
- Wu, H.X.; Hao, H.T.; Lei, H.; Ge, Y.; Shi, H.; Song, Y. Farm Size, Risk Aversion and Overuse of Fertilizer: The Heterogeneity of Large-Scale and Small-Scale Wheat Farmers in Northern China. Land 2021, 10, 111. [Google Scholar] [CrossRef]
- Wei, H.; Li, J. Efficiency performance of fertilizer use in arable agricultural production in China. China Agric. Econ. Rev. 2019, 11, 52–69. [Google Scholar] [CrossRef]
- Qiu, H.G.; Luan, H. Effect of risk aversion on farmers’ excessive use of fertilizer. Chin. Rural Econ. 2014, 3, 85–96. [Google Scholar]
- Shi, C.L.; Zhu, J.F. Economic evaluation and analysis of chemical fertilizer inputs in Chinese grain production. J. Arid. Land Resour. Environ. 2016, 30, 57–63. [Google Scholar] [CrossRef]
- Hu, L.X.; Zhang, X.H.; Zhou, Y.H. Farm size and fertilizer sustainable use: An empirical study in Jiangsu, China. J. Integr. Agric. 2019, 18, 2898–2909. [Google Scholar] [CrossRef]
- Wu, Y.R. Chemical Fertilizer Use Efficiency and its Determinants in China′s Farming Sector. China Agric. Econ. Rev. 2011, 3, 117–130. [Google Scholar] [CrossRef]
- Bai, X.G.; Wang, Y.N.; Huo, X.X.; Salim, R.; Bloch, H.; Zhang, H. Assessing fertilizer use efficiency and its determinants for apple production in China. Ecol. Indic. 2019, 104, 268–278. [Google Scholar] [CrossRef]
- Konradsen, F.; Hoek, W.V.D.; Cole, D.C.; Hutchinson, G.; Daisley, H.; Singh, S.; Eddleston, M. Reducing acute poisoning in developing countries--options for restricting the availability of pesticides. Toxicology 2003, 192, 249–261. [Google Scholar] [CrossRef]
- Wang, H.L.; Peng, H.; Shen, C.Y.; Wu, Z. Effect of irrigation amount and fertilization on agriculture non-point source pollution in the paddy field. Environ. Sci. Pollut. Res. 2019, 26, 10363–10373. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Zhang, J.B.; Li, H.P. Research on spatial-temporal characteristics and affecting factors decomposition of agricultural carbon emission in China. China Popul. Resour. Environ. 2011, 21, 80–86. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, H. Verification of environmental Kuznets curve of agricultural non-point source pollution—Analysis based on time Series data of Jiangsu Province. Chin. Rural Econ. 2009, 4, 48–53. [Google Scholar]
- Cao, D.Y.; Li, G.C. Empirical research on the agricultural environmental Kuznets curve in China. Soft Sci. 2011, 25, 76–80. [Google Scholar]
- Zhang, T.; Ni, J.P.; Xie, D.T. Assessment of the relationship between rural non-point source pollution and economic development in the Three Gorges Reservoir Area. Environ. Sci. Pollut. Res. 2016, 23, 8125–8132. [Google Scholar] [CrossRef]
- Dogan, E.; Seker, F. An investigation on the determinants of carbon emissions for OECD countries: Empirical evidence from panel models robust to heterogeneity and cross-sectional dependence. Environ. Sci. Pollut. Res. 2016, 23, 14646–14655. [Google Scholar] [CrossRef]
- Yu, D.H.; Zhang, M.Z. Resolution of “the heterogeneity difficulty” and re-verification of the carbon emission EKC: Based on the country grouping test under the threshold regression. China Ind. Econ. 2016, 07, 57–73. [Google Scholar] [CrossRef]
- Zou, Q. Environmental Kuznets curve for China′s carbon emission: An empirical study based on panel threshold regression method. China Econ. Stud. 2015, 4, 86–99. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Effects of population and affluence on CO2 emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.M. Measurement of input-output elasticity of regional agricultural production factors in China: Empirical evidence based on spatial econometric model. Chin. Rural Econ. 2010, 06, 25–37. [Google Scholar]
- Wang, Y.; Zhu, Y.; Zhang, S.; Wang, Y. What could promote farmers to replace chemical fertilizers with organic fertilizers? J. Clean. Prod. 2018, 199, 882–890. [Google Scholar] [CrossRef]
- Tone, K.A. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Tone, K.A. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.Y.; Zhang, W.G. A research of agricultural eco-efficiency measure in China and space-time differences. China Popul. Resour. Environ. 2016, 26, 11–19. [Google Scholar] [CrossRef]
- Li, T.P.; Zhang, F.; Hu, H. Authentication of the Kuznets curve in agriculture non-point source pollution and its drivers analysis. China Popul. Resour. Environ. 2011, 21, 118–123. [Google Scholar] [CrossRef]
- Lai, S.Y.; Du, P.F.; Chen, J.N. Evaluation of non-point source pollution based on unit analysis. J. Tsinghua Univ. (Sci. Technol.) 2004, 9, 1184–1187. [Google Scholar] [CrossRef]
- Wu, X.Q.; Wang, Y.P.; He, L.M.; Lu, G.F. Agricultural eco-efficiency evaluation based on AHP and DEA model: A case of Wuxi City. Resour. Environ. Yangtze Basin 2012, 21, 714–719. [Google Scholar]
- Dietz, T.; Rosa, E.A. Rethinking the environmental impacts of population, Affluence and technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar] [CrossRef]
- Li, K.M.; Fang, L.T. Profile estimation of spatial lag quantile regression model. J. Quant. Tech. Econ. 2018, 35, 144–161. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, K.N.; Sun, W.Y. Urbanization, education quality, and middle-income trap. J. Quant. Tech. Econ. 2018, 35, 40–58. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression for Longitudinal Data. J. Multivar. Anal. 2004, 91, 74–89. [Google Scholar] [CrossRef] [Green Version]
- Yuan, P.; Xu, Y.; Liu, H.Y. Does Chinese manufacturing firms’ growth conform to the Gibrat’s law? Ind. Econ. Res. 2017, 6, 26–37. [Google Scholar] [CrossRef]
- Hou, M.Y.; Yao, S.B. Spatial-temporal evolution and trend prediction of agricultural eco-efficiency in China: 1978-2016. Acta Geogr. Sin. 2018, 73, 2168–2183. [Google Scholar] [CrossRef]
- Georgopoulou, A.; Angelis-Dimakis, A.; Arampatzis, G.; Assimacopoulos, D. Improving the eco-efficiency of an agricultural water use system. Desalin. Water Treat. 2016, 57, 11484–11493. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Li, Z.; Wang, L. Temporal-spatial differences in and influencing factors of agricultural eco-efficiency in Shandong province, China. Ciência Rural 2020, 50, 1–13. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometric: Methods and Models. J. Am. Stat. Assoc. 1990, 85, 160. [Google Scholar]
- Anselin, L. Spatial Econometrics; Bruton Center School of Social Sciences, University of Texas: Richardson, TX, USA, 1999. [Google Scholar]
- Liu, J.M.; Ouyang, L.; Mao, J. Fiscal decentralization, economic growth and government poverty reduction. China Soft Sci. 2018, 139–150. [Google Scholar]
- Yu, Y.Z. Estimation of total factor productivity in China from the perspective of heterogeneity: 1978–2012. China Econ. Q. 2017, 16, 1051–1072. [Google Scholar] [CrossRef]
- Zhang, X.S.; Dai, Y.A. Heterogeneity, fiscal decentralization, and urban economic growth—A study based on a panel quantile regression model. J. Financ. Res. 2012, 01, 103–115. [Google Scholar]
- Pan, X.D.; Li, P.; Feng, Z.Z.; Duan, C.Q. Spatial and Temporal Variations in Fertilizer Use Across Prefecture-level Cities in China from 2000 to 2015. Environ. Sci. 2019, 40, 4733–4742. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Arzeni, A.; Bodini, A. Assessing eco-efficiency of arable farms in rural areas. Agric. Syst. 2017, 151, 114–125. [Google Scholar] [CrossRef]
- Maia, R.; Silva, C.; Costa, E. Eco-efficiency assessment in the agricultural sector: The Monte Novo irrigation perimeter, Portugal. J. Clean. Prod. 2016, 138, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Xu, J. Analyses of carbon reduction potential of low carbon technologies in China. Issues Agric. Econ. 2022, 03, 117–135. [Google Scholar] [CrossRef]
- Aryal, J.P.; Sapkota, T.B.; Krupnik, T.J.; Rahut, D.B.; Jat, M.L.; Stirling, C.M. Factors affecting farmers’ use of organic and inorganic fertilizers in South Asia. Environ. Sci. Pollut. Res. 2021, 28, 51480–51496. [Google Scholar] [CrossRef]
- Li, S.; Wu, J.; Wang, X.; Ma, L. Economic and environmental sustainability of maize-wheat rotation production when substituting mineral fertilizers with manure in the north China plain. J. Clean. Prod. 2020, 271, 122683. [Google Scholar] [CrossRef]



| Indicators | Variables | Variable Description | Remarks |
|---|---|---|---|
| Elemental inputs (x) | Land | Total crop sown area/khm2 | Reflects the actual cultivated area in agricultural production |
| Labor | Agricultural employees/104 people | Primary industry employees × (Gross agricultural product/Gross output of agriculture, forestry, animal husbandry and fishery) | |
| Mechanical | Total power of machinery/104 kW | Agricultural machinery is a representative tool of agricultural modernization | |
| Water | Effective irrigation area/khm2 | To characterize the irrigation level of agricultural water | |
| Fertilizer | Fertilizer use amount/104 t | Fertilizer, pesticide, agricultural film, diesel fuel are the main sources of pollution in the agricultural production process | |
| Pesticide | Pesticide use amount/104 t | ||
| Plastic film | Film use amount/104 t | ||
| Energy | Diesel consumption amount/104 t | ||
| Desired outputs (yd) | Economic output | Gross agricultural product/100 million CNY | Converted to constant price in 1978 to eliminate the effect of price changes |
| Non-desired outputs (yu) | Pollution emission | Agricultural non-point source pollution/104 t | Fertilizer loss, ineffective pesticide utilization, and agricultural film residue |
| Variable/Unit | Variable Definition | Mean | Std. Dev. | Min | Max | |
|---|---|---|---|---|---|---|
| Explained variable | Agricultural eco-efficiency (AEE) | Measurement based on super-efficient SBM model | 0.474 | 0.334 | 0.085 | 2.385 |
| Core explanatory variable | Fertilizer use intensity (FUI)/(kg/hm2) | Agricultural fertilizer use/total crop sown area | 249.540 | 139.066 | 9.170 | 799.590 |
| Independent variables | Rural Labor Transfer (RLT)/(104 people) | Rural employees—agricultural employees | 445.942 | 497.162 | 1.400 | 2226.640 |
| Disposable income of rural households (DIR)/(CNY) | Disposable income of rural households per capita | 4412.624 | 5548.311 | 100.930 | 34,911.000 | |
| Machinery input intensity (MII)/(kW/hm2) | Total power of agricultural machinery/total crop sown area | 158.396 | 52.700 | 43.050 | 285.850 | |
| Multiple cropping index (MCI)/(%) | Total crop sown area/cropland area | 3.795 | 2.801 | 0.289 | 14.156 | |
| Crop planting structure (CPS)/(%) | Grain crop planting area/total crop sown area | 70.558 | 11.952 | 32.810 | 97.080 | |
| Fiscal Supporting on Agriculture (FSA)/(CNY/hm2) | Fiscal expenditure on agriculture, forestry and water affairs/total crop sown area | 9.871 | 5.298 | 0.415 | 67.321 | |
| Original Variables | LLC | IPS | ADF-Fisher | Harris-Tzavalis | VIF | ||||
|---|---|---|---|---|---|---|---|---|---|
| Value | p | Value | p | Value | p | Value | p | ||
| lnFUI | −4.435 | 0.000 | −7.933 | 0.000 | −6.033 | 0.000 | 0.739 | 0.000 | 4.34 |
| lnRLT | −1.753 | 0.039 | −5.043 | 0.000 | −3.924 | 0.000 | 0.702 | 0.000 | 2.10 |
| lnDIR | −2.213 | 0.014 | −5.563 | 0.000 | −2.428 | 0.007 | 0.796 | 0.031 | 5.01 |
| lnMII | −1.865 | 0.023 | −0.907 | 0.182 | −3.457 | 0.000 | 0.978 | 0.000 | 4.12 |
| lnMCI | −1.960 | 0.017 | −4.840 | 0.000 | −1.890 | 0.029 | 0.692 | 0.000 | 1.95 |
| lnCPS | −1.417 | 0.078 | −4.314 | 0.000 | −2.923 | 0.002 | 0.797 | 0.033 | 1.45 |
| lnFSA | −4.347 | 0.000 | −9.206 | 0.000 | −7.010 | 0.000 | 0.728 | 0.000 | 1.11 |
| Quantile | lnFUI | lnRLT | lnDIR | lnMII | lnMCI | lnCPS | lnFSA | C | R2 |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | −0.338 *** (0.035) | −0.141 *** (0.016) | 0.466 *** (0.018) | 0.129 *** (0.037) | −0.287 *** (0.053) | −0.304 *** (0.081) | −0.004 (0.022) | −1.897 *** (0.487) | 0.606 |
| θ = 10% | −0.211 *** (0.026) | −0.124 *** (0.008) | 0.387 *** (0.032) | −0.028 (0.021) | −0.131 *** (0.032) | −0.390 *** (0.051) | −0.040 *** (0.018) | −0.118 (0.362) | 0.562 |
| θ = 20% | −0.154 *** (0.023) | −0.169 *** (0.008) | 0.327 *** (0.028) | −0.004 (0.018) | 0.012 (0.028) | −0.308 *** (0.045) | −0.044 *** (0.017) | −0.872 *** (0.320) | 0.566 |
| θ = 30% | −0.171 *** (0.023) | −0.202 *** (0.008) | 0.268 *** (0.029) | 0.082 *** (0.019) | 0.126 *** (0.029) | −0.227 *** (0.047) | −0.068 *** (0.017) | −1.141 *** (0.331) | 0.563 |
| θ = 40% | −0.163 *** (0.027) | −0.235 *** (0.009) | 0.226 *** (0.034) | 0.120 *** (0.022) | 0.199 *** (0.034) | −0.261 *** (0.054) | −0.080 *** (0.020) | −0.862 *** (0.382) | 0.540 |
| θ = 50% | −0.157 *** (0.029) | −0.269 *** (0.010) | 0.163 *** (0.036) | 0.141 *** (0.024) | 0.261 *** (0.037) | −0.339 *** (0.058) | −0.136 *** (0.021) | −0.086 (0.411) | 0.529 |
| θ = 60% | −0.158 *** (0.031) | −0.294 *** (0.010) | 0.146 *** (0.038) | 0.173 *** (0.025) | 0.319 *** (0.039) | −0.358 *** (0.061) | −0.135 ** (0.023) | −0.051 (0.433) | 0.524 |
| θ = 70% | −0.144 *** (0.035) | −0.316 *** (0.012) | 0.148 *** (0.044) | 0.168 *** (0.029) | 0.341 *** (0.044) | −0.409 *** (0.070) | −0.110 *** (0.026) | 0.154 (0.494) | 0.514 |
| θ = 80% | −0.065 * (0.036) | −0.368 *** (0.012) | 0.235 *** (0.046) | 0.082 *** (0.030) | 0.382 *** (0.046) | −0.517 *** (0.074) | −0.029 (0.027) | 1.116 *** (10.97) | 0.509 |
| θ = 90% | −0.127 *** (0.036) | −0.381 *** (0.012) | 0.323 *** (0.046) | 0.020 (0.030) | 0.298 *** (0.046) | −0.668 *** (0.073) | 0.007 (0.026) | 1.263 ** (0.518) | 0.485 |
| lnFUI | Economic Sub-Divisions | Sub-Periods | |||||
|---|---|---|---|---|---|---|---|
| ER | CR | WR | NER | 1978–1989 | 1990–2003 | 2004–2020 | |
| Baseline | −0.702 *** (0.060) | −0.445 *** (0.071) | −0.095 * (0.055) | −0.384 *** (0.125) | −0.006 (0.042) | −0.179 ** (0.079) | −0.077 (0.095) |
| θ = 10% | 0.029 (0.052) | 0.147 ** (0.069) | −0.218 *** (0.045) | −0.185 *** (0.030) | −0.193 *** (0.057) | −0.294 *** (0.054) | 0.159 *** (0.039) |
| θ = 20% | 0.104 ** (0.049) | 0.106 ** (0.049) | −0.118 *** (0.047) | −0.185 *** (0.034) | −0.065 (0.052) | −0.178 *** (0.043) | 0.085 ** (0.038) |
| θ = 30% | 0.148 *** (0.043) | 0.017 (0.048) | −0.101 ** (0.046) | −0.185 *** (0.037) | −0.053 (0.052) | −0.139 *** (0.038) | 0.084 ** (0.037) |
| θ = 40% | 0.035 (0.040) | −0.013 (0.039) | −0.104 ** (0.046) | −0.224 *** (0.022) | −0.038 (0.050) | −0.126 *** (0.041) | 0.126 *** (0.039) |
| θ = 50% | −0.043 (0.041) | −0.044 (0.043) | −0.016 (0.043) | −0.229 *** (0.018) | −0.030 (0.051) | −0.099** (0.044) | 0034 (0.037) |
| θ = 60% | −0.091 ** (0.042) | 0.032 (0.035) | −0.020 (0.046) | −0.266 *** (0.025) | 0.039 (0.050) | −0.129 ** (0.050) | −0.041 (0.039) |
| θ = 70% | −0.136 *** (0.047) | −0.010 (0.048) | −0.061 (0.044) | −0.324 *** (0.046) | 0.071 (0.052) | −0.163 *** (0.055) | −0.080 * (0.041) |
| θ = 80% | −0.113 ** (0.053) | 0.184 *** (0.054) | −0.131 *** (0.047) | −0.324 *** (0.043) | 0.109 ** (0.054) | −0.244 *** (−0.054) | −0.125 *** (0.045) |
| θ = 90% | −0.136 ** (0.062) | 0.213 *** (0.058) | −0.171 *** (0.048) | −0.324 *** (0.038) | 0.113 ** (0.055) | −0.256 *** (0.060) | −0.187 *** (0.051) |
| lnFUI | Wq | Wd | Wa | |||
|---|---|---|---|---|---|---|
| lnFUI | Wq × lnFUI | lnFUI | Wd × lnFUI | lnFUI | Wa × lnFUI | |
| θ = 10% | −0.281 *** (0.026) | −0.020 *** (0.003) | −0.166 *** (0.025) | 0.691 *** (0.086) | −0.196 *** (0.025) | 0.210 *** (0.031) |
| θ = 20% | −0.228 *** (0.023) | −0.016 *** (0.003) | −0.118 ** (0.022) | 0.780 *** (0.073) | −0.127 *** (0.021) | 0.256 *** (0.026) |
| θ = 30% | −0.223 *** (0.024) | −0.020 *** (0.003) | −0.151 *** (0.024) | 0.961 *** (0.078) | −0.166 *** (0.023) | 0.329 *** (0.028) |
| θ = 40% | −0.215 *** (0.026) | −0.022 *** (0.003) | −0.138 *** (0.025) | 1.170 *** (0.084) | −0.132 *** (0.026) | 0.382 *** (0.032) |
| θ = 50% | −0.226 *** (0.026) | −0.024 *** (0.003) | −0.095 *** (0.028) | 1.282 *** (0.093) | −0.134 *** (0.028) | 0.389 *** (0.035) |
| θ = 60% | −0.201 *** (0.029) | −0.021 *** (0.004) | −0.059 *** (0.028) | 1.422 *** (0.095) | −0.116 *** (0.029) | 0.426 *** (0.035) |
| θ = 70% | −0.161 *** (0.035) | −0.013 *** (0.004) | 0.012 (0.029) | 1.508 *** (0.097) | −0.055 *** (0.029) | 0.437 *** (0.036) |
| θ = 80% | −0.047 (0.035) | 0.009 ** (0.004) | 0.022 (0.028) | 1.480 *** (0.095) | 0.014 (0.030) | 0.472 *** (0.037) |
| θ = 90% | −0.134 *** (0.036) | 0.007 * (0.004) | 0.031 (0.032) | 1.561 *** (0.105) | 0.057 * (0.033) | 0.446 *** (0.041) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, M.; Xi, Z.; Zhao, S. Evaluating the Heterogeneity Effect of Fertilizer Use Intensity on Agricultural Eco-Efficiency in China: Evidence from a Panel Quantile Regression Model. Int. J. Environ. Res. Public Health 2022, 19, 6612. https://doi.org/10.3390/ijerph19116612
Hou M, Xi Z, Zhao S. Evaluating the Heterogeneity Effect of Fertilizer Use Intensity on Agricultural Eco-Efficiency in China: Evidence from a Panel Quantile Regression Model. International Journal of Environmental Research and Public Health. 2022; 19(11):6612. https://doi.org/10.3390/ijerph19116612
Chicago/Turabian StyleHou, Mengyang, Zenglei Xi, and Suyan Zhao. 2022. "Evaluating the Heterogeneity Effect of Fertilizer Use Intensity on Agricultural Eco-Efficiency in China: Evidence from a Panel Quantile Regression Model" International Journal of Environmental Research and Public Health 19, no. 11: 6612. https://doi.org/10.3390/ijerph19116612
APA StyleHou, M., Xi, Z., & Zhao, S. (2022). Evaluating the Heterogeneity Effect of Fertilizer Use Intensity on Agricultural Eco-Efficiency in China: Evidence from a Panel Quantile Regression Model. International Journal of Environmental Research and Public Health, 19(11), 6612. https://doi.org/10.3390/ijerph19116612