New Framework for Dynamic Water Environmental Capacity Estimation Integrating the Hydro-Environmental Model and Load–Duration Curve Method—A Case Study in Data-Scarce Luanhe River Basin
Abstract
:1. Introduction
- (1)
- Provide a more applicable method for in-stream WEC calculation in developing regions based on a modified pollutant control strategy;
- (2)
- Discuss the impact mechanisms of hydrological and temperature conditions on WEC in detail and establish the real-time responses of WEC to these factors;
- (3)
- Integrate the modified WEC estimation method and the real-time response process to develop a hydro-environmental model for dynamic WEC estimation;
- (4)
- Combine the SWAT model and LDC method to present a spatiotemporal distribution of WEC under different hydrological regimes; identify the hot spots of fragile regions and periods; and provide suggestions for managers about the collaborative pollutant control at a basin scale.
2. Materials and Methods
2.1. Study Site
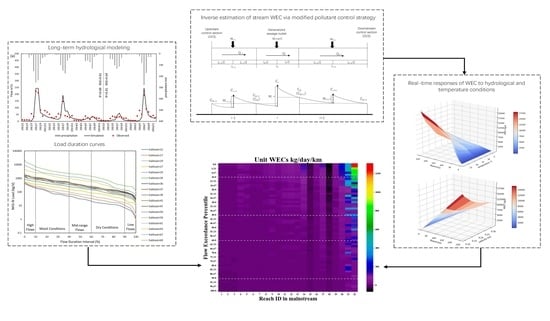
2.2. Integrated Framework for Dynamic Water Environmental Capacity Estimation
2.2.1. SWAT Model Setup and Evaluation
2.2.2. Modified Hydro-Environmental Model Establishment
Water Environmental Capacity Calculation
Model Parameters Determinations
3. Results
3.1. Historical Flow Estimation Based on SWAT Model and Traditional LDC Creating
3.2. The Calibration of Integrated Degradation Coefficient and Relevant Influencing Factors
3.3. The Results of the Modified Hydro-Environmental Model
4. Discussion
4.1. Estimation of the Water Environmental Capacity
4.2. Effects of Hydrological and Temperature Conditions on WEC
4.3. Application of the Method to Multi-Segments and Management Implications
5. Conclusions
- (1)
- Hydrological conditions play a dominant role in WEC regulation. In the Luanhe River basin, 77% of the capacities were concentrated in high flows and moist conditions, and mainly from July to September. It would be more reasonable if the basin sewage discharge strategies were regulated according to different FDIs rather than a single low flow condition.
- (2)
- The increase in flow velocity indeed promoted the decay rate of pollutants in the river, but shortened the traveling time within the calculated units, leading to the pollutants being washed downstream without adequate degradation, which eventually reduced the channel WEC.
- (3)
- Considering the maldistribution of WECs between the upper and downstream, the point sources of pollution, e.g., sewage treatment plants, should be planned to avoid fragile regions of the upper and middle reaches.
- (4)
- A coordinated water quality control should be implemented in the fragile reaches (e.g., Reach 15 and Reach 18 in Luanhe River), improving the quality standard of their adjacent upstream reaches to give space for local hydro-environmental restoration. Otherwise, the fragile reaches will hardly meet the standard, even if they have not discharged sewage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Levashova, E.A.; Mikhailov, V.N.; Mikhailova, M.V.; Morozov, V.N. Natural and Human-Induced Variations in Water and Sediment Runoff in the Danube River Mouth. Water Resour. 2004, 31, 235–246. [Google Scholar] [CrossRef]
- Jiang, Y. China’s Water Security: Current Status, Emerging Challenges and Future Prospects. Environ. Sci. Policy 2015, 54, 106–125. [Google Scholar] [CrossRef]
- Li, R.; Zou, Z. Water Environmental Capacity Analysis of Taihu Lake and Parameter Estimation Based on the Integration of the Inverse Method and Bayesian Modeling. Int. J. Environ. Res. Public Health 2015, 12, 12212–12224. [Google Scholar] [CrossRef] [Green Version]
- CAEP. Guidance for Determination of National Water Environmental Capacity; CEAP: Beijing, China, 2003; pp. 1–77. [Google Scholar]
- Li, Y.; Qiu, R.; Yang, Z.; Li, C.; Yu, J. Parameter Determination to Calculate Water Environmental Capacity in Zhangweinan Canal Sub-Basin in China. J. Environ. Sci. 2010, 22, 904–907. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Bao, Q.; Qi, Z. On Regional Differentiation of River Water Environment Capacity and Strategies to Control Water Environment Pollution in China. Chin. Geogr. Sci. 1995, 5, 116–124. [Google Scholar] [CrossRef]
- USEPA. Protocol for Developing Pathogen TMDLs, 1st ed.; USEPA: Washington, DC, USA, 2001; p. 132. [Google Scholar]
- Havens, K.E.; Walker, W.W. Development of a Total Phosphorus Concentration Goal in the TMDL Process for Lake Okeechobee, Florida (USA). Lake Reserv. Manag. 2002, 18, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Kang, M.S.; Park, S.W.; Lee, J.J.; Yoo, K.H. Applying SWAT for TMDL Programs to a Small Watershed Containing Rice Paddy Fields. Agric. Water Manag. 2006, 79, 72–92. [Google Scholar] [CrossRef]
- Fan, C.; Chen, K.H.; Huang, Y.Z. Model-Based Carrying Capacity Investigation and Its Application to Total Maximum Daily Load (TMDL) Establishment for River Water Quality Management: A Case Study in Taiwan. J. Clean. Prod. 2021, 291, 125251. [Google Scholar] [CrossRef]
- Lee, C.S.; Wen, C.G. River Assimilative Capacity Analysis via Fuzzy Linear Programming. Fuzzy Sets Syst. 1996, 79, 191–201. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, Y.; Wang, J.H.; Xiao, W.H.; Jarsjö, J.; Huang, Y.; Liu, Y.; Wu, J.P.; Wang, H.-J. Urban Closed Lakes: Nutrient Sources, Assimilative Capacity and Pollutant Reduction under Different Precipitation Frequencies. Sci. Total Environ. 2020, 700, 134531. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, S.; Liu, J.; Liu, C.; Hao, F.; Wang, Z.; Zhang, H.; Song, J.; Mitrovic, S.M.; Lim, R.P. Linking Fish Tolerance to Water Quality Criteria for the Assessment of Environmental Flows: A Practical Method for Streamflow Regulation and Pollution Control. Water Res. 2018, 141, 96–108. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, X.H.; Xu, C.Y.; Wang, H.; Lei, X.H.; Wang, X.; Li, S.Y. Development of Load Duration Curve System in Data-Scarce Watersheds Based on a Distributed Hydrological Model. Hydrol. Res. 2019, 50, 886–900. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Jia, H.; Yang, C.; Melching, C.; Yuan, Y. A Pollutant Load Hierarchical Allocation Method Integrated in an Environmental Capacity Management System for Zhushan Bay, Taihu Lake. Sci. Total Environ. 2015, 533, 223–237. [Google Scholar] [CrossRef]
- Li, S.; Morioka, T. Optimal Allocation of Waste Loads in a River with Probabilistic Tributary Flow Under Transverse Mixing. Water Environ. Res. 1999, 71, 156–162. [Google Scholar] [CrossRef]
- Revelle, C.S.; Lynn, R. To Water Quality Management—Primary Treatment Secondary Treatment LiTeHi Ry Treatment. Water Resour. Res. 1968, 4, 1–9. [Google Scholar] [CrossRef]
- USEPA. Fecal Coliform TMDL for Horseshoe Creek; USEPA: Atlanta, GA, USA, 2007. [Google Scholar]
- Johnson, S.L.; Whiteaker, T.; Maidment, D.R. A Tool for Automated Load Duration Curve Creation. J. Am. Water Resour. Assoc. 2009, 45, 654–663. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, R.; Men, C.; Guo, L.; Miao, Y. Temporal-Spatial Analysis of Water Environmental Capacity Based on the Couple of SWAT Model and Differential Evolution Algorithm. J. Hydrol. 2019, 569, 155–166. [Google Scholar] [CrossRef]
- Shen, J.; Zhao, Y. Combined Bayesian Statistics and Load Duration Curve Method for Bacteria Nonpoint Source Loading Estimation. Water Res. 2010, 44, 77–84. [Google Scholar] [CrossRef]
- Bai, H.; Zhao, C.; Chen, Y.; Zhao, Y.; Dai, W. Study on Water Environmental Capacity Calculation and Emission Reduction Benefit Assessment of Wulie River in Chengde City. Environ. Pollut. Control 2015, 37, 31–34. [Google Scholar] [CrossRef]
- Yu, X.; Geng, Y.; Heck, P.; Xue, B. A Review of China’s Rural Water Management. Sustainability 2015, 7, 5773–5792. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.S.; Yang, S.T.; Sun, Y.; Zhang, H.T.; Sun, C.L.; Xu, T.R.; Lim, R.P.; Mitrovic, S.M. Estimating River Accommodation Capacity for Organic Pollutants in Data-Scarce Areas. J. Hydrol. 2018, 564, 442–451. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Q.; Li, Z.; Li, R. Uncertainty Analyses on the Calculation of Water Environmental Capacity by an Innovative Holistic Method and Its Application to the Dongjiang River. J. Environ. Sci. 2014, 26, 1783–1790. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.; Gao, Y.; Li, L.; Gao, J. Estimation of Water Environmental Capacity and Pollution Load Reduction for Urban Lakeside of Lake Taihu, Eastern China. Ecol. Eng. 2019, 139, 105587. [Google Scholar] [CrossRef]
- Zhang, H. Research on Dynamic Characteristics of River Pollution Degradation Coefficient in the Main Stream of Weihe River. J. Phys. Conf. Ser. 2020, 1549, 22050. [Google Scholar] [CrossRef]
- Chapra, S.C.; Pelletier, G.J.; Tao, H. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality, Version 2.12. Doc. User Man. 2012, 97. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, J.; Cheng, W.; Song, C.; Cao, G. The Comparison of the Environmental Capacity Calculation Methods. J. Xian Univ. Technol. 1999, 4710, 1–6. [Google Scholar]
- Arnold, J.G.; Williams, J.R.; Srinivasan, R.; King, K.W.; Griggs, R.H. SWAT: Soil and Water Assessment Tool; Agriculture Research Service, Grassland, Soil and Water Research Laboratory: Temple, TX, USA, 1994. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current Capabilities and Research Opportunities in Applied Watershed Modelling. Hydrol. Processes 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Dong, G.; Yang, Z.; Shi, X.; Yu, Y. Runoff Simulation of Huangfuchuan Watershed Based on SWAT Model. Yellow River 2013, 35, 6–10. [Google Scholar]
- Qiu, H.; Qi, J.; Lee, S.; Moglen, G.E.; McCarty, G.W.; Chen, M.; Zhang, X. Effects of Temporal Resolution of River Routing on Hydrologic Modeling and Aquatic Ecosystem Health Assessment with the SWAT Model. Environ. Model. Softw. 2021, 146, 105232. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Shi, C.; Wu, Y.; Ji, X. Establishment and Evaluation of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS). Water 2018, 10, 1555. [Google Scholar] [CrossRef] [Green Version]
- Wieder, W.R.; Boehnert, J.; Bonan, G.B.; Langseth, M. Regridded Harmonized World Soil Database v1.2. Data Set; ORNL DAAC: Oak Ridge, TN, USA, 2014. [Google Scholar]
- Zhang, L.; Meng, X.; Wang, H.; Yang, M.; Cai, S. Investigate the Applicability of CMADS and CFSR Reanalysis in Northeast China. Water 2020, 12, 996. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Zhang, X.; Yang, M.; Wang, H.; Chen, J.; Pan, Z.; Wu, Y. Application and Evaluation of the China Meteorological Assimilation Driving Datasets for The Swat Model (CMADS) in Poorly Gauged Regions in Western China. Water 2019, 11, 2171. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Wang, H.; Chen, J.; Yang, M.; Pan, Z. High-Resolution Simulation and Validation of Soil Moisture in the Arid Region of Northwest China. Sci. Rep. 2019, 9, 17227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, X.; Wang, H.; Wu, Y.; Long, A.; Wang, J.; Shi, C.; Ji, X. Investigating spatiotemporal changes of the land-surface processes in Xinjiang using high-resolution CLM3. 5 and CLDAS: Soil temperature. Sci. Rep. 2017, 7, 13286. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H. Significance of the China Meteorological Assimilation Driving Datasets for the SWAT Model (CMADS) of East Asia. Water 2017, 9, 765. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Chen, J. Profound Impacts of the China Meteorological Assimilation Dataset for the SWAT Model (CMADS). Water 2019, 11, 832. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Parajuli, P.; Nelson, N.; Frees, L.; Mankin, K. Advanced Bash-Scripting Guide An in-Depth Exploration of the Art of Shell Scripting Table of Contents. Hydrol. Processes 2010, 2274, 2267–2274. [Google Scholar]
- Malik, M.A.; Dar, A.Q.; Jain, M.K. Modelling Streamflow Using the SWAT Model and Multi-Site Calibration Utilizing SUFI-2 of SWAT-CUP Model for High Altitude Catchments, NW Himalaya’s. Modeling Earth Syst. Environ. 2022, 8, 1203–1213. [Google Scholar] [CrossRef]
- Saleh, F.; Ducharne, A.; Flipo, N.; Oudin, L.; Ledoux, E. Impact of River Bed Morphology on Discharge and Water Levels Simulated by a 1D Saint-Venant Hydraulic Model at Regional Scale. J. Hydrol. 2013, 476, 169–177. [Google Scholar] [CrossRef]
- Elberling, B. Temperature and Oxygen Control on Pyrite Oxidation in Frozen Mine Tailings. Cold Reg. Sci. Technol. 2005, 41, 121–133. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T.J. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications (USGS Numbered Series No. 252); Professional Paper; U. S. Government Printing Office: Washington, DC, USA, 1953; 57p. [Google Scholar]
- Ministry of Water Resources of the People’s republic of China. Annual Hydrological Report: The Third Volume, Hydrological Data of Haihe River Basin; Ministry of Water Resources Press, PRC: Beijing, China, 2017. [Google Scholar]
- Geng, X.; Zhou, X.; Yin, G.; Hao, F.; Zhang, X.; Hao, Z.; Singh, V.P.; Fu, Y.H. Extended Growing Season Reduced River Runoff in Luanhe River Basin. J. Hydrol. 2020, 582, 124538. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Xie, J.; Luo, J.; Yan, L. Research on Dynamic Characteristics of River Pollution Degradation Coefficient between Longmen and Sanmenxia on the Yellow River. J. Xi’an Univ. Technol. 2012, 28, 293–297. [Google Scholar] [CrossRef]
- Shan, D. Calculation and Study on Degradation Coefficient of Ammonia Nitrogen in North Canal. Ph.D. Thesis, Capital Normal University, Beijing, China, 2013. [Google Scholar]
- Liu, Q.; Jiang, J.; Jing, C.; Qi, J. Spatial and Seasonal Dynamics of Water Environmental Capacity in Mountainous Rivers of the Southeastern Coast, China. Int. J. Environ. Res. Public Health 2018, 15, 99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, A.; Cho, S.; Park, M.J.; Kim, S. Determination of Standard Target Water Quality in the Nakdong River Basin for the Total Maximum Daily Load Management System in Korea. KSCE J. Civ. Eng. 2013, 17, 309–319. [Google Scholar] [CrossRef]
- Cho, J.H.; Lee, J.H. Watershed Model Calibration Framework Developed Using an Influence Coefficient Algorithm and a Genetic Algorithm and Analysis of Pollutant Discharge Characteristics and Load Reduction in a TMDL Planning Area. J. Environ. Manag. 2015, 163, 2–10. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, P.; Hu, C.; Guo, H. Water Quality Modeling for Load Reduction under Uncertainty: A Bayesian Approach. Water Res. 2008, 42, 3305–3314. [Google Scholar] [CrossRef]
- Hadwen, W.L.; Fellows, C.S.; Westhorpe, D.P.; Rees, G.N.; Mitrovic, S.M.; Taylor, B.; Baldwin, D.S.; Silvester, E.; Croome, R. Longitudinal Trends in River Functioning: Patterns of Nutrient and Carbon Processing in Three Australian Rivers. River Res. Appl. 2010, 26, 1129–1152. [Google Scholar] [CrossRef] [Green Version]
- Novotny, V. Simplified databased total maximum daily loads, or the world is log-normal. J. Environ. Eng. 2004, 130, 674–683. [Google Scholar] [CrossRef]
- Baohui, M.; Xiaoyun, N.; Canjun, L.; Jing, C.; Jingjing, L. Water Environmental Capacity Calculation and Initial Distribution for Typical of Luanhe River Basin. Water Resour. Prot. 2021, 38, 9. [Google Scholar]
- Li, X.; Li, C.; Wang, X.; Liu, Q.; Yi, Y.; Zhang, X. A Developed Method of Water Pollution Control Based on Environmental Capacity and Environmental Flow in Luanhe River Basin. Water 2022, 14, 730. [Google Scholar] [CrossRef]
- de Castro-Català, N.; Kuzmanovic, M.; Roig, N.; Sierra, J.; Ginebreda, A.; Barceló, D.; Pérez, S.; Petrovic, M.; Picó, Y.; Schuhmacher, M.; et al. Ecotoxicity of Sediments in Rivers: Invertebrate Community, Toxicity Bioassays and the Toxic Unit Approach as Complementary Assessment Tools. Sci. Total Environ. 2016, 540, 297–306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, K.; Hu, Y.; Xie, J. Estimation and Allocation of Water Environment Capacity in the First-Grade Protecting Area of Miyun Reservoir Based on One-Point Source Pollutions. Chin. J. Agric. Resour. Reg. Plan. 2016, 37, 10–17. [Google Scholar]
- Wojtkowska, M.; Bogacki, J.; Witeska, A. Assessment of the Hazard Posed by Metal Forms in Water and Sediments. Sci. Total Environ. 2016, 551–552, 387–392. [Google Scholar] [CrossRef] [PubMed]














| Luanxian | Wulongji | |||||||
|---|---|---|---|---|---|---|---|---|
| Calibration | PR | Validation | PR | Calibration | PR | Validation | PR | |
| R2 | 0.88 | Very good | 0.81 | Very good | 0.86 | Very good | 0.7 | Good |
| NSE | 0.81 | Very good | 0.64 | Adequate | 0.65 | Very good | 0.67 | Very good |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Chen, W.; Zhao, Z.; Wang, J.; Ma, W. New Framework for Dynamic Water Environmental Capacity Estimation Integrating the Hydro-Environmental Model and Load–Duration Curve Method—A Case Study in Data-Scarce Luanhe River Basin. Int. J. Environ. Res. Public Health 2022, 19, 8389. https://doi.org/10.3390/ijerph19148389
Jin H, Chen W, Zhao Z, Wang J, Ma W. New Framework for Dynamic Water Environmental Capacity Estimation Integrating the Hydro-Environmental Model and Load–Duration Curve Method—A Case Study in Data-Scarce Luanhe River Basin. International Journal of Environmental Research and Public Health. 2022; 19(14):8389. https://doi.org/10.3390/ijerph19148389
Chicago/Turabian StyleJin, Huiyu, Wanqi Chen, Zhenghong Zhao, Jiajia Wang, and Weichun Ma. 2022. "New Framework for Dynamic Water Environmental Capacity Estimation Integrating the Hydro-Environmental Model and Load–Duration Curve Method—A Case Study in Data-Scarce Luanhe River Basin" International Journal of Environmental Research and Public Health 19, no. 14: 8389. https://doi.org/10.3390/ijerph19148389
APA StyleJin, H., Chen, W., Zhao, Z., Wang, J., & Ma, W. (2022). New Framework for Dynamic Water Environmental Capacity Estimation Integrating the Hydro-Environmental Model and Load–Duration Curve Method—A Case Study in Data-Scarce Luanhe River Basin. International Journal of Environmental Research and Public Health, 19(14), 8389. https://doi.org/10.3390/ijerph19148389