Improved Covariance Matrix Estimation for Portfolio Risk Measurement: A Review
Abstract
:1. Introduction
2. Fat tail of Financial Data and Data Dependence
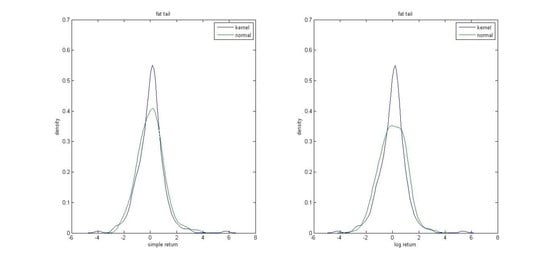
2.1. The Concept of Fat Tails
2.2. The Dependence of Financial Data
3. Portfolio Selection: A Review of Common Models
3.1. Mean-Variance Model
3.2. Global Minimum Variance Model
4. Factor Model
4.1. Single Factor Models
4.2. Multi-Factor Models
5. Portfolio Risk Measure
5.1. Moment-Based Risk Measurement
5.1.1. Time-Varying Covariance Matrix
5.1.2. Shrinkage Estimation
5.2. Moment-Based and Quantile-Based Risk Measurement
5.2.1. VaR and CVaR
5.2.2. Semi-Variance
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Abanto-Valle, C. A., V. H. Lachos, and Dipak K. Dey. 2015. Bayesian estimation of a skew-Student-t stochastic volatility model. Methodology and Computing in Applied Probability 17: 721–38. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Francesco Franzoni. 2009. Learning about beta: Time-varying factor loadings, expected returns, and the conditional capm. Journal of Empirical Finance 16: 537–56. [Google Scholar] [CrossRef]
- Albanese, Claudio, and Giuseppe Campolieti. 2006. Advanced Derivatives Pricing and Risk Management. Diego: Elsevier Academic Press. [Google Scholar]
- Albanese, Claudio, Kenneth Jackson, and Petter Wiberg. 2004. A new Fourier transform algorithm for value-at-risk. Quantitative Finance 4: 328–38. [Google Scholar] [CrossRef]
- Alexander, Carol. 2001. Orthogonal GARCH. Mastering Risk 2: 21–38. [Google Scholar]
- Alimi, Amir, Mostafa Zandieh, and Maghsoud Amiri. 2012. Multi-objective portfolio optimization of mutual funds under downside risk measure using fuzzy theory. International Journal of Industrial Engineering Computations 3: 859–72. [Google Scholar] [CrossRef]
- Anyfantaki, Sofia, and Antonis Demos. 2016. Estimation and properties of a time-varying EGARCH (1,1) in mean model. Econometric Reviews 35: 293–310. [Google Scholar] [CrossRef]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1997. Thinking coherently. Risk 10: 68–71. [Google Scholar]
- Asai, Manabu. 2008. Autoregressive stochastic volatility models with heavy-tailed distributions: A comparison with multifactor volatility models. Journal of Empirical Finance 15: 332–41. [Google Scholar] [CrossRef]
- Asai, Manabu. 2009. Bayesian analysis of stochastic volatility models with mixture-of-normal distributions. Mathematics and Computers in Simulation 79: 2579–96. [Google Scholar] [CrossRef]
- Ausin, Concepcion, and Hedibert Lopes. 2010. Time-varying joint distribution through copulas. Computational Statistics and Data Analysis 54: 2383–99. [Google Scholar] [CrossRef]
- Bai, Jushan. 2003. Inferential theory for factor models of large dimensions. Econometrica 71: 135–71. [Google Scholar] [CrossRef]
- Bai, Jushan, and Shuzhong Shi. 2011. Estimating high dimensional covariance matrices and its applications. Annals of Economics and Finance 12: 199–215. [Google Scholar]
- Ballestero, Enrique. 2005. Mean-semivariance efficient frontier: A downside risk model for portfolio selection. Applied Mathematical Finance 12: 1–15. [Google Scholar] [CrossRef]
- Bartram, Söhnke, Stephen Taylor, and Yaw-Huei Wang. 2007. The euro and European financial market integration. Journal of Banking and Finance 31: 1461–81. [Google Scholar] [CrossRef]
- Basak, Suleyman, and Alexander Shapiro. 2001. Value-at-risk-based risk management: Optimal policies and asset prices. Review of Financial Studies 14: 371–405. [Google Scholar] [CrossRef]
- Batten, Jonathan, Harald Kinateder, and Niklas Wagner. 2014. Multifractality and value-at-risk forecasting of exchange rates. Physica A Statistical Mechanics and Its Applications 401: 71–81. [Google Scholar] [CrossRef]
- Baumol, William. 1952. The transactions demand for cash: An inventory theoretic approach. Quarterly Journal of Economics 66: 545–56. [Google Scholar] [CrossRef]
- Bauwens, Luc, and Sebastien Laurent. 2005. A new class of multivariate skew densities, with application to generalized autoregressive conditional heteroscedasticity models. Journal of Business and Economic Statistics 23: 346–54. [Google Scholar] [CrossRef]
- Bawa, Vijay. 1978. Safety-first, stochastic dominance, and optimal portfolio choice. Journal of Financial and Quantitative Analysis 13: 255–71. [Google Scholar] [CrossRef]
- Bawa, Vijay, and Eric Lindenberg. 1977. Capital market equilibrium in a mean-lower partial moment framework. Journal of Financial Economics 12: 635–35. [Google Scholar]
- Beder, Tanya. 1995. VAR: Seductive but Dangerous. Financial Analysts Journal 51: 12–24. [Google Scholar] [CrossRef]
- Benninga, S. Z., and Z. Wiener. 1998. Value-at-Risk (VaR). Mathematica in Education and Research 7: 39–45. [Google Scholar]
- Bera, Anil, Philip Garcia, and Jae-Sun Roh. 1997. Estimation of Time-Varying Hedging Ratios for Corn and Soybeans: BGARCH and Random Coefficient Approaches. Sankhya: Series B 59: 346–68. [Google Scholar]
- Bernardino, Di, J. M. Fernández-Ponce, F. Palacios-Rodríguez, and M. R. Rodríguez-Griñolo. 2014. On multivariate extensions of the conditional Value-at-Risk measure. Insurance: Mathematics and Economics 61: 1–16. [Google Scholar] [CrossRef]
- Bi, J., Y. Zhong, and X. Y. Zhou. 2013. Mean-semivariance portfolio selection under probability distortion. Stochastics: An International Journal of Probability and Stochastic Processes: Formerly Stochastics and Stochastics Reports 85: 604–19. [Google Scholar] [CrossRef]
- Bickel, Peter, and Elizaveta Levina. 2008a. Covariance regularization by thresholding. Annals of Statistics 36: 2577–604. [Google Scholar] [CrossRef]
- Bickel, Peter, and Elizaveta Levina. 2008b. Regularized estimation of large covariance matrices. Annals of Statistics 36: 199–227. [Google Scholar] [CrossRef]
- Boasson, Vigdis, Emil Boasson, and Zhao Zhou. 2011. Portfolio Optimization in a Mean-Semivariance Framework. Investment Management and Financial Innovations 8: 58–68. [Google Scholar]
- Bodnar, Taras, and Wolfgang Schmid. 2008. A test for the weights of the global minimum variance portfolio in an elliptical model. Metrika 67: 127–43. [Google Scholar] [CrossRef]
- Bodnar, Taras, and Wolfgang Schmid. 2009. Econometrical analysis of the sample efficient frontier. European Journal of Finance 15: 317–35. [Google Scholar] [CrossRef]
- Bodnar, Taras, Stepan Mazur, and Krzysztof Podgórski. 2016. Singular inverse Wishart distribution and its application to portfolio theory. Journal of Multivariate Analysis 143: 314–26. [Google Scholar] [CrossRef]
- Bodnar, Taras, Stepan Mazur, and Yarema Okhrin. 2017. Bayesian estimation of the global minimum variance portfolio. European Journal of Operational Research 256: 292–307. [Google Scholar] [CrossRef]
- Bodnar, Taras, Nestor Parolya, and Wolfgang Schmid. 2018. Estimation of the global minimum variance portfolio in high dimensions. European Journal of Operational Research 266: 371–90. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Robert F. Engle, and Jeffrey M. Wooldridge. 1988. A capital asset pricing model with time-varying covariances. The Journal of Political Economy 96: 116–31. [Google Scholar] [CrossRef]
- Brito, Rui Pedro, Hélder Sebastião, and Pedro Godinho. 2016. Efficient skewness/semivariance portfolios. Journal of Asset Management 17: 331–46. [Google Scholar] [CrossRef]
- Cai, Tony, and Weidong Liu. 2011. Adaptive thresholding for sparse covariance matrix estimation. Journal of the American Statistical Association 106: 672–84. [Google Scholar] [CrossRef]
- Campbell, John. 1996. Understanding risk and return. Journal of Political Economy 104: 298–345. [Google Scholar] [CrossRef]
- Campbell, Rachel, Ronald Huisman, and Kees Koedijk. 2001. Optimal portfolio selection in a value-at-risk framework. Journal of Banking and Finance 25: 1789–804. [Google Scholar] [CrossRef]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Cardinali, Alessandro. 2012. An Out-of-sample Analysis of Mean-Variance Portfolios with Orthogonal GARCH Factors. International Econometric Review 4: 1–16. [Google Scholar]
- Carroll, Rachael, Thomas Conlon, John Cotter, and Enrique Salvador. 2017. Asset allocation with correlation: A composite trade-off. European Journal of Operational Research 262: 1164–80. [Google Scholar] [CrossRef]
- Castellacci, Giuseppe, and Michael J. Siclari. 2003. The practice of Delta-Gamma VaR: Implementing the quadratic portfolio model. European Journal of Operational Research 150: 529–45. [Google Scholar] [CrossRef]
- Castellano, Rosella, and Roy Cerqueti. 2014. Mean-variance portfolio selection in presence of infrequently traded stocks. European Journal of Operational Research 234: 442–49. [Google Scholar] [CrossRef]
- Chabaane, Ali, J. Laurent, Yannik Malevergne, and Francoise Turpin. 2006. Alternative risk measures for alternative investments. Journal of Risk 8: 1–32. [Google Scholar] [CrossRef]
- Chan, Louis K. C., Jason Karceski, and Josef Lakonishok. 1999. On portfolio optimization: Forecasting covariances and choosing the risk model. The Review of Financial Studies 12: 937–74. [Google Scholar] [CrossRef]
- Chang, Yi-Ping, Jing-Xiu Lin, and Chih-Tun Yu. 2016. Calculating Value-at-Risk Using the Granularity Adjustment Method in the Portfolio Credit Risk Model with Random Loss Given Default. Journal of Economics and Management 12: 157–76. [Google Scholar]
- Chen, Ren-Raw, and Louis Scott. 1993. Maximum likelihood estimation for a multi-factor equilibrium model of the term structure of interest rates. The Journal of Fixed Income 3: 14–31. [Google Scholar] [CrossRef]
- Chen, Yi-Hsuan, and Anthony H. Tu. 2013. Estimating hedged portfolio value-at-risk using the conditional Copula: An illustration of model risk. International Review of Economics and Finance 27: 514–28. [Google Scholar] [CrossRef]
- Chen, Hung-Hsin, and Chang-Biau Yang. 2017. Multiperiod portfolio investment using stochastic programming with conditional value at risk. Computers and Operations Research 81: 305–21. [Google Scholar] [CrossRef]
- Chen, Rongda, and Lean Yu. 2013. A novel nonlinear value-at-risk method for modeling risk of option portfolio with multivariate mixture of normal distributions. Economic Modelling 35: 796–804. [Google Scholar] [CrossRef]
- Chen, Chia Lin, Saeed Maghsoodloo, and Chan Park. 1991. A Method for Approximating Semivariance in Project Portfolio Analysis. The Engineering Economist 37: 33–59. [Google Scholar] [CrossRef]
- Chen, Yilun, Ami Wiesel, Yonina Eldar, and Alfred Hero. 2010. Shrinkage algorithms for MMSE covariance estimation. IEEE Transactions on Signal Processing 58: 5016–29. [Google Scholar] [CrossRef]
- Chen, Lin, Jin Peng, Bo Zhang, and Isnaini Rosyida. 2017. Diversified models for portfolio selection based on uncertain semivariance. International Journal of Systems Science 48: 637–48. [Google Scholar] [CrossRef]
- Chen, Wei, Dandan Li, Shan Lu, and Weiyi Liu. 2018. Multi-period mean-semivariance portfolio optimization based on uncertain measure. Soft Computing, 1–17. [Google Scholar] [CrossRef]
- Chiah, Mardy, Daniel Chai, Angel Zhong, and Song Li. 2016. A better model? An empirical investigation of the Fama-French Five-factor model in Australia. International Review of Finance 16: 595–638. [Google Scholar]
- Chib, Siddhartha, Federico Nardari, and Neil Shephard. 2002. Markov chain monte carlo methods for stochastic volatility models. Journal of Econometrics 108: 281–316. [Google Scholar] [CrossRef]
- Chin, Wen Cheong. 2008. Heavy-tailed value-at-risk analysis for Malaysian stock exchange. Physica A 387: 4285–98. [Google Scholar] [CrossRef]
- Choobineh, F. Fred, and D. L. Branting. 1986. A simple approximation for semivariance. European Journal of Operational Research 27: 364–70. [Google Scholar] [CrossRef]
- Chopra, Vijay K., and William T. Ziemba. 1993. The effect of errors in means, variances, and covariances on optimal portfolio choice. Journal of Portfolio Management 19: 6–12. [Google Scholar] [CrossRef]
- Chow, K. Victor, William B. Riley, and John P. Formby. 1992. International portfolio selection and efficiency analysis. Review of Quantitative Finance and Accounting 2: 47–67. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Vihang Errunza, Kris Jacobs, and Hugues Langlois. 2012. Is the Potential for International Diversification Disappearing? A Dynamic Copula Approach. Review of Financial Studies 25: 3711–51. [Google Scholar] [CrossRef]
- Clarke, Roger G., Harindra De Silva, and Steven Thorley. 2006. Minimum-variance portfolios in the U.S. equity market. Journal of Portfolio Management 33: 10–24. [Google Scholar] [CrossRef]
- Conrad, Christian, and Enno Mammen. 2016. Asymptotics for parametric GARCH-in-Mean models. Journal of Econometrics 194: 319–29. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Costa, Oswaldo L. V., and Rodrigo de Barros Nabholz. 2002. A linear matrix inequalities approach to robust mean-semivariance portfolio optimization. Applied Optimization 74: 89–107. [Google Scholar]
- Creal, Drew D., and Ruey S. Tsay. 2015. High dimensional dynamic stochastic Copula models. Journal of Econometrics 189: 335–45. [Google Scholar] [CrossRef]
- Cui, Xueting, Shushang Zhu, Xiaoling Sun, and Duan Li. 2013. Nonlinear portfolio selection using approximate parametric Value-at-Risk. Journal of Banking and Finance 37: 2124–39. [Google Scholar] [CrossRef]
- Cumova, Denisa, and David Nawrocki. 2011. A symmetric LPM model for heuristic mean-semivariance analysis. Journal of Economics and Business 63: 217–36. [Google Scholar] [CrossRef]
- Dai, Min, and Yifei Zhong. 2008. Penalty Methods for Continuous-Time Portfolio Selection with Proportional Transaction Costs. Social Science Electronic Publishing 13: 1–31. [Google Scholar] [CrossRef]
- Date, Paresh, and Roberto Bustreo. 2016. Measuring the risk of a non-linear portfolio with fat-tailed risk factors through a probability conserving transformation. Ima Journal of Management Mathematics 27: 157–80. [Google Scholar] [CrossRef]
- Davis, Mark H. A., and Andrew R. Norman. 1990. Portfolio Selection with Transaction Costs. Mathematics of Operations Research 15: 676–713. [Google Scholar] [CrossRef]
- Delatola, Eleni Ioanna, and Jim E. Griffin. 2013. A bayesian semiparametric model for volatility with a leverage effect. Computational Statistics and Data Analysis 60: 97–110. [Google Scholar] [CrossRef]
- Demiguel, Victor, and Francisco J Nogales. 2009. Portfolio selection with robust estimation. Operations Research 57: 560–77. [Google Scholar] [CrossRef]
- Diamantopoulos, Konstantinos, and Ioannis Vrontos. 2010. A Student-t Full Factor Multivariate GARCH Model. Computational Economics 35: 63–83. [Google Scholar] [CrossRef]
- Dias, Gustavo Fruet. 2017. The time-varying GARCH-in-mean model. Economics Letters 157: 129–32. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Marc Nerlove. 1989. The Dynamics of Exchange Rate Volatility: A Multivariate Latent Factor ARCH Model. Journal of Applied Econometrics 4: 1–21. [Google Scholar] [CrossRef]
- Diβmann, J., E. C. Brechmann, C. Czado, and D. Kurowicka. 2013. Selecting and estimating regular vine copula and application to financial returns. Computational Statistics and Data Analysis 59: 52–69. [Google Scholar]
- Duffie, Darrell, and Rui Kan. 1996. A yield-factor model of interest rates. Mathematical Finance 6: 379–406. [Google Scholar] [CrossRef]
- Dumas, Bernard, and Elisa Luciano. 1991. An exact solution to a dynamic portfolio choice problem under transactions costs. The Journal of Finance 46: 577–95. [Google Scholar] [CrossRef]
- Eldomiaty, Tarek. 2007. Can the Normality of the Semi Variance Be Improved? Evidence from Financial Stock Indexes with Hourly, Daily, Quarterly and Annual Data of DJIA and SP500. Applied Econometrics and International Development 7: 95–108. [Google Scholar]
- Embrechts, Paul. 1999. Extreme Value Theory as a Risk Management Tool. North American Actuarial Journal 3: 30–41. [Google Scholar] [CrossRef]
- Embrechts, Paul, Alexander J. Mcneil, and Daniel Straumann. 1999. Correlation: Pitfalls and alternatives. Risk 12: 69–71. [Google Scholar]
- Embrechts, Paul, Alexander J. Mcneil, and Daniel Straumann. 2001. Correlation and dependency in risk management: Properties and pitfalls. In Risk Management: Value at Risk and Beyond. Edited by Dempster Michael Alan Howarth. Cambridge: Cambridge University Press. [Google Scholar]
- Engle, Robert. 1982. Autoregressive conditional heteroscedasticity and estimates of UK inflation. Econometrica 50: 987–1008. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic conditonal correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate simultaneous generalized ARCH. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Engle, Robert F., Clive W. J. Granger, and Dennis Kraft. 1984. Combining competing forecasts of inflation using a bivariate ARCH model. Journal of Economic Dynamics and Control 8: 151–65. [Google Scholar] [CrossRef]
- Engle, Robert F., Victor K. Ng, and Michael Rothschild. 1990. Asset pricing with a factor-arch covariance structure: Empirical estimates for treasury bills. Journal of Econometrics 45: 213–37. [Google Scholar] [CrossRef]
- Estrada, Javier. 2004. Mean-Semivariance Behaviour: An Alternative Behavioural Model. Journal of Emerging Market Finance 3: 231–48. [Google Scholar] [CrossRef]
- Fama, Eugene. 1965. The behavior of stock market prices. Journal of Business 38: 34–105. [Google Scholar] [CrossRef]
- Fama, Eugene, and K. R. French. 1993. Common risk factors in the returns on stocks and bonds. The Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics 16: 1–22. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2016. Dissecting Anomalies with a Five-Factor Model. Review of Financial Studies 29: 69–103. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2017. International tests of a five-factor asset pricing model. Journal of Financial Economics 123: 441–63. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Richard Roll. 1968. Some properties of symmetric stable distributions. Journal of the American Statistical Association 63: 817–36. [Google Scholar]
- Fan, Jianqing, Yuan Liao, and Martina Mincheva. 2013. Large covariance estimation by thresholding principal orthogonal complements. Journal of the Royal Statistical Society: Series B 75: 603–80. [Google Scholar] [CrossRef]
- Fernández, Alberto, and Sergio Gómez. 2007. Portfolio selection using neural networks. Computers and Operations Research 34: 1177–91. [Google Scholar] [CrossRef]
- Fishburn, Peter. 1977. Mean-risk analysis with risk associated with below-target returns. The American Economic Review 67: 116–26. [Google Scholar]
- Fisher, Thomas J., and Xiaoqian Sun. 2011. Improved Stein-type shrinkage estimators for the high-dimensional multivariate normal covariance matrix. Computational Statistics and Data Analysis 55: 1909–18. [Google Scholar] [CrossRef]
- Frahm, Gabriel. 2010. Linear statistical inference for global and local minimum variance portfolios. Statistical Papers 51: 789–812. [Google Scholar] [CrossRef]
- Fraiman, Ricardo, and Beatriz Pateiro-López. 2012. Quantiles for finite and infinite dimensional data. Journal of Multivariate Analysis 108: 1–14. [Google Scholar] [CrossRef]
- Friedman, Daniel, and Stoddard Vandersteel. 1982. Short-run fluctuations in foreign exchange rates. Journal of International Economics 13: 171–86. [Google Scholar] [CrossRef]
- Frost, Peter A., and James E. Savarino. 1986. An Empirical Bayes Approach to Efficient Portfolio Selection. Journal of Financial and Quantitative Analysis 21: 293–305. [Google Scholar] [CrossRef]
- Gaivoronski, Alexei A, and Georg Ch Pflug. 2005. Value at risk in portfolio optimization: Properties and computational approach. Journal of Risk 7: 1–31. [Google Scholar] [CrossRef]
- Gao, Jianjun, Duan Li, Xiangyu Cui, and Shouyang Wang. 2015. Time cardinality constrained mean–variance dynamic portfolio selection and market timing: A stochastic control approach. Automatica 54: 91–99. [Google Scholar] [CrossRef]
- Garcia, René, and Georges Tsafack. 2011. Dependence structure and extreme comovements in international equity and bond markets. Journal of Banking and Finance 35: 1954–70. [Google Scholar] [CrossRef]
- Geidosch, Marco, and Matthias Fischer. 2016. Application of Vine Copulas to Credit Portfolio Risk Modeling. Journal of Risk and Financial Management 9: 4. [Google Scholar] [CrossRef]
- Geweke, John. 1977. The dynamic factor analysis of economic time series. In Latent Variables in Socio-Economic Models. Edited by Dennis Aigner and Goldberger Arthur. Amsterdam: North-Holland, pp. 365–83. [Google Scholar]
- Geweke, John, and Kenneth Singleton. 1981. Maximum likelihood confirmatory factor analysis of economic time series. International Economic Review 22: 37–54. [Google Scholar] [CrossRef]
- Ghaoui, Laurent El, Maksim Oks, and Francois Oustry. 2003. Worst-case Value-at-Risk and robust portfolio optimization: A conic programming approach. Operations Research 51: 543–56. [Google Scholar] [CrossRef]
- Ghose, Devajyoti, and Kenneth F. Kroner. 1995. The relationship between GARCH and symmetric stable processes: Finding the source of fat tails in financial data. Journal of Empirical Finance 2: 225–51. [Google Scholar] [CrossRef]
- Giacomini, Enzo, Wolfgang Karl Karl Härdle, and Vladimir G. Spokoiny. 2009. Inhomogeneous dependency modelling with time varying copulae. Journal of Business and Economic Statistics 27: 224–34. [Google Scholar] [CrossRef]
- Giot, Pierre. 2005. Market risk models for intraday data. The European Journal of Finance 11: 309–24. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2004. Monte Carlo Methods in Financial Engineering. New York: Springer. [Google Scholar]
- Glombek, Konstantin. 2014. Statistical Inference for High-Dimensional Global Minimum Variance Portfolios. Scandinavian Journal of Statistics 41: 845–65. [Google Scholar] [CrossRef]
- Goldfarb, Donald, and Garud Iyengar. 2003. Robust portfolio selection problems. Mathematics of Operations Research 28: 1–38. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1993. On the use of mean-variance and quadratic approximations in implementing dynamic investment strategies: A comparison of returns and investment policies. Management Science 39: 856–71. [Google Scholar] [CrossRef]
- Grauer, Robert R., and Nils H. Hakansson. 1995. Stein and CAPM estimators of the means in asset allocation. International Review of Financial Analysis 4: 35–66. [Google Scholar] [CrossRef]
- Grootveld, Henk, and Winfried Hallerbach. 1999. Variance vs downside risk: Is there really that much difference? European Journal of Operational Research 114: 304–19. [Google Scholar] [CrossRef]
- Gunay, Samet, and Audil Rashid Khaki. 2018. Best Fitting Fat Tail Distribution for the Volatilities of Energy Futures: Gev, Gat and Stable Distributions in GARCH and APARCH Models. Journal of Risk and Financial Management 11: 30. [Google Scholar] [CrossRef]
- Haas, Markus, Stefan Mittnik, and Marc S. Paolella. 2009. Asymmetric multivariate normal mixture GARCH. Computational Statistics and Data Analysis 53: 2129–54. [Google Scholar] [CrossRef]
- Hafner, Christian M., and Philip Hans Franses. 2009. A Generalized Dynamic Conditional Correlation Model: Simulation and Application to Many Assets. Econometric Reviews 28: 612–31. [Google Scholar] [CrossRef]
- Hafner, Christian M., and Hans Manner. 2012. Dynamic stochastic copula models: Estimation, inference and applications. Journal of Applied Econometrics 27: 269–95. [Google Scholar] [CrossRef]
- Hafner, Christian M., and Olga Reznikova. 2010. Efficient estimation of a semiparametric dynamic copula model. Computational Statistics and Data Analysis 54: 2609–27. [Google Scholar] [CrossRef]
- Hallin, Marc, Davy Paindaveine, and Miroslav Siman. 2010. Multivariate quantiles and multiple output regression quantiles: From L1 optimization to half space depth. Annals of Statistics 38: 635–69. [Google Scholar] [CrossRef]
- Hamza, Faris, and Jacques Janssen. 1998. The mean-semivariances approach to realistic portfolio optimization subject to transaction costs. Applied Stochastic Models in Business and Industry 14: 275–83. [Google Scholar] [CrossRef]
- Han, Yufeng. 2006. Asset allocation with a high dimensional latent factor stochastic volatility model. Review of Financial Studies 19: 237–71. [Google Scholar] [CrossRef]
- Hardle, Wolfgang, Kleinow Torstein, and Stahl Gerhard. 2002. Applied Quantitative Finance. New York: Springer. [Google Scholar]
- Haugen, Robert A., and Nardin L. Baker. 1991. The efficient market inefficiency of capitalization-weighted stock portfolios. Journal of Portfolio Management 17: 35–40. [Google Scholar] [CrossRef]
- Heyde, Chris, Shuangzhe Liu, and Roger Gay. 2001. Fractal scaling and Black-Scholes: The full story. JASSA Autumn, 29–32. [Google Scholar]
- Hogan, William W., and James M. Warren. 1972. Computation of the Efficient Boundary in the E-S Portfolio Selection Model. Journal of Financial and Quantitative Analysis 7: 1881–96. [Google Scholar] [CrossRef]
- Hogan, William W., and James M. Warren. 1974. Toward the Development of an Equilibrium Capital-Market Model Based on Semivariance. Journal of Financial and Quantitative Analysis 9: 1–11. [Google Scholar] [CrossRef]
- Hou, Kewei, Chen Xue, and Lu Zhang. 2015. Digesting anomalies: An investment approach. Review of Financial Studies 28: 650–705. [Google Scholar] [CrossRef]
- Hu, Ling. 2006. Dependence patterns across financial markets: A mixed copula approach. Applied Financial Economics 16: 717–29. [Google Scholar] [CrossRef]
- Huang, Hung-Hsi. 2006. Optimal insurance contract under value-at-risk constraint. The Geneva Risk and Insurance Review 31: 91–110. [Google Scholar] [CrossRef]
- Huang, Xiaoxia. 2008. Mean-semivariance models for fuzzy portfolio selection. Journal of Computational and Applied Mathematics 217: 1–8. [Google Scholar] [CrossRef]
- Huang, Dashan, Shushang Zhu, Frank J. Fabozzi, and Masao Fukushima. 2010. Portfolio selection under distributional uncertainty: A relative robust CVaR approach. European Journal of Operational Research 203: 185–94. [Google Scholar] [CrossRef]
- Huang, Xiaoxia, Tianyi Zhao, and Shamsiya Kudratova. 2016. Uncertain mean-variance and mean-semivariance models for optimal project selection and scheduling. Knowledge-Based Systems 93: 1–11. [Google Scholar] [CrossRef]
- Ikeda, Yuki, and Tatsuya Kubokawa. 2016. Linear shrinkage estimation of large covariance matrices using factor models. Journal of Multivariate Analysis 152: 61–81. [Google Scholar] [CrossRef]
- Jagannathan, Ravi, and Tongshu Ma. 2003. Risk reduction in large portfolios: Why imposing the wrong constraints helps? Journal of Finance 58: 1651–83. [Google Scholar] [CrossRef]
- Jahankhani, Ali. 1976. E-V and E-S Capital Asset Pricing Models: Some Empirical Tests. The Journal of Financial and Quantitative Analysis 11: 513–28. [Google Scholar] [CrossRef]
- Jang, Bong-Gyu, and Seyoung Park. 2016. Ambiguity and optimal portfolio choice with Value-at-Risk constraint. Finance Research Letters 18: 158–76. [Google Scholar] [CrossRef]
- Jin, Hanqing, Harry Markowitz, and Xun Yu Zhou. 2006. A note on semivariance. Mathematical Finance 16: 53–61. [Google Scholar] [CrossRef]
- Jobson, Dave, and Robert (Bob) Michael Korkie. 1980. Estimation for Markowitz efficient portfolios. Journal of the American Statistical Association 75: 544–54. [Google Scholar] [CrossRef]
- Joe, Harry. 1997. Multivariate Models and Dependence Concepts. London: CRC Press. [Google Scholar]
- Siven, Johannes Vitalis, Jeffrey Todd Lins, and Anna Szymkowiak-Have. 2009. Value-at-Risk computation by Fourier inversion with explicit error bonds. Finance Research Letters 6: 95–105. [Google Scholar] [CrossRef]
- Jorion, Philippe. 1985. International Portfolio Diversification with Estimation Risk. Journal of Business 58: 259–78. [Google Scholar] [CrossRef]
- Jorion, Philippe. 1991. Bayesian and CAPM estimators of the means: Implications for portfolio selection. Journal of Banking and Finance 15: 717–27. [Google Scholar] [CrossRef]
- Jorion, Philippe. 1996. Risk 2: Measuring Risk in a Value at Risk. Financial Analysts Journal 52: 47–56. [Google Scholar] [CrossRef]
- Josephy, Norman H., and Amir D. Aczel. 1993. A statistically optimal estimator of semivariance. European Journal of Operational Research 67: 267–71. [Google Scholar] [CrossRef]
- Jungbacker, Borus, and Siem Jan Koopman. 2015. Likelihood-based dynamic factor analysis for measurement and forecasting. Econometrics Journal 18: C1–C21. [Google Scholar] [CrossRef]
- Jungbacker, Borus, Siem Jan Koopman, and Michel van der Wel. 2014. Smooth dynamic factor analysis with an application to the US term structure of interest rates. Journal of Applied Econometrics 29: 65–90. [Google Scholar] [CrossRef]
- Kan, Raymond, and Guofu Zhou. 2007. Optimal Portfolio Choice with Parameter Uncertainty. The Journal of Financial and Quantitative Analysis 42: 621–56. [Google Scholar] [CrossRef]
- Kaplan, Paul D., and Rodney H. Alldredge. 1997. Semivariance in Risk-Based Index Construction: Quantidex Global Indexe. Journal of Investing 6: 82–87. [Google Scholar] [CrossRef]
- Karatzas, Ioannis, John P. Lehoczky, and Steven E. Shreve. 1987. Optimal portfolio and consumption decisions for a “small investor” on a finite horizon. SIAM Journal on Control and Optimization 25: 1557–86. [Google Scholar] [CrossRef]
- Kausky, Carolyn, and Roger M. Cooke. 2009. The Unholy Trinity: Fat Tails, Tail Dependence, and Micro-Correlations, Discussion Paper, Resources for the Future. Available online: http://www.rff.org/files/sharepoint/WorkImages/Download/RFF-DP-09-36-REV.pdf (accessed on 24 December 2018).
- Kempf, Alexander, and Christoph Memmel. 2006. Estimating the global minimum variance portfolio. Schmalenbach Business Review 58: 332–48. [Google Scholar] [CrossRef]
- Kibzun, Andrey I., and Evgeniy A. Kuznetsov. 2006. Analysis of criteria VaR and CVaR. Journal of Banking and Finance 30: 779–96. [Google Scholar] [CrossRef]
- King, Mervyn, and Sushil Wadhwani. 1990. Transmission of Volatility between Stock Markets. Review of Financial Studies 3: 5–33. [Google Scholar] [CrossRef]
- Klein, Tony, and Thomas Walther. 2016. Oil price volatility forecast with mixture memory GARCH. Energy Economics 58: 46–58. [Google Scholar] [CrossRef]
- Kole, Erik, Kees Koedijk, and Marno Verbeek. 2007. Selecting Copulas for risk management. Journal of Banking and Finance 31: 2405–23. [Google Scholar] [CrossRef]
- Konno, Yoshihiko. 2009. Shrinkage estimators for large covariance matrices in multivariate real and complex normal distributions under an invariant quadratic loss. Journal of Multivariate Analysis 100: 2237–53. [Google Scholar] [CrossRef]
- Kourtis, Apostolos, George Dotsis, and Raphael N. Markellos. 2012. Parameter uncertainty in portfolio selection: Shrinkage the inverse covariance matrix. Journal of Banking and Finance 36: 2522–31. [Google Scholar] [CrossRef]
- Kroner, Kenneth F., and Stijn Claessens. 1991. Optimal dynamic hedging portfolios and the currency composition of external debt. Journal of International Money and Finance 10: 131–48. [Google Scholar] [CrossRef]
- Kubota, Keiichi, and Hitoshi Takehara. 2018. Does the Fama and French Five-Factor Model Work Well in Japan? International Review of Finance 18: 137–46. [Google Scholar] [CrossRef]
- LeBaron, Blake, and Ritirupa Samanta. 2004. Extreme Value Theory and Fat Tails in Equity Markets. Available online: https://pdfs.semanticscholar.org/a45c/60df4c29c1cd55cd28f3cd5b4299cc2a4032.pdf (accessed on 14 December 2018).
- Lafosse, Patricia Lengua, and Gabriel Rodríguez. 2018. An empirical application of a stochastic volatility model with GHSkew Student’s t-distribution to the volatility of Latin-American stock returns. Quarterly Review of Economics and Finance 69: 155–73. [Google Scholar] [CrossRef]
- Lanne, Markku, and Pentti Saikkonen. 2007. A Multivariate Generalized Orthogonal Factor GARCH Model. Journal of Business and Economic Statistics 25: 61–75. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2003. Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance 10: 603–21. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2004. A well-conditioned estimator for large-dimensional covariance matrices. Journal of Multivariate Analysis 88: 365–411. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2012. Nonlinear shrinkage estimation of large-dimensional covariance matrices. Annals of Statistics 40: 1024–60. [Google Scholar] [CrossRef]
- Ledoit, Olivier, Pedro Santaclara, and Michael Wolf. 2003. Flexible multivariate GARCH modeling with an application to international stock markets. Review of Economics and Statistics 85: 735–47. [Google Scholar] [CrossRef]
- Lee, Wayne Y., and Ramesh K. S. Rao. 1988. Mean Lower Partial Moment Valuation and Lognormally Distributed Returns. Management Science 34: 446–53. [Google Scholar] [CrossRef]
- Lewis, Alan L. 1990. Semivariance and the Performance of Portfolios with Options. Financial Analysts Journal 46: 67–76. [Google Scholar] [CrossRef]
- Li, Duan, and Wanlung Ng. 2000. Optimal dynamic portfolio selection: Multiperiod mean-variance formulation. Mathematical Finance 10: 387–406. [Google Scholar] [CrossRef]
- Li, Chen, Zhonghua Lu, Yonghong Hu, Fang Liu, and Jue Wang. 2018. A Parallel Hybrid Intelligent Algorithm for Fuzzy Mean-CVaR Portfolio Model. Paper presented at IEEE International Conference on High PERFORMANCE Computing and Communications; IEEE, International Conference on Smart City; IEEE, International Conference on Data Science and Systems, Bangkok, Thailand, December 18–20. [Google Scholar]
- Liagkouras, Konstantinos, and Kostas S. Metaxiotis. 2018. Multi-period mean-variance fuzzy portfolio optimization model with transaction costs. Engineering Applications of Artificial Intelligence 67: 260–69. [Google Scholar] [CrossRef]
- Lien, Donald, and Xiangdong Luo. 1994. Multiperiod hedging in the presence of conditional heteroscedasticity. Journal of Futures Markets 14: 927–55. [Google Scholar] [CrossRef]
- Lien, Donald, Yiu Kuen Tse, and Albert K. Tsui. 2002. Evaluating the hedging performance of the constant-correlation GARCH model. Applied Financial Economics 12: 791–98. [Google Scholar] [CrossRef]
- Liesenfeld, Roman, and Robert C. Jung. 2000. Stochastic volatility models: Conditional normality versus heavy-tailed distributions. Journal of Applied Econometrics 15: 137–60. [Google Scholar] [CrossRef]
- Lioui, Abraham, and Patrice Poncet. 2016. Understanding dynamic mean variance asset allocation. European Journal of Operational Research 254: 320–37. [Google Scholar] [CrossRef]
- Litterman, Robert B., and Josè Scheinkman. 1991. Common factors affecting bond returns. The Journal of Fixed Income 47: 129–282. [Google Scholar] [CrossRef]
- Liu, Shuangzhe, and Chris C. Heyde. 2008. On estimation in conditional heteroskedastic time series models under non-normal distributions. Statistical Papers 49: 455–69. [Google Scholar] [CrossRef]
- Liu, Yan, and Richard Luger. 2009. Efficient estimation of copula-GARCH models. Computational Statistics and Data Analysis 53: 2284–97. [Google Scholar] [CrossRef]
- Liu, Yong-Jun, and Wei-Guo Zhang. 2015. A multi-period fuzzy portfolio optimization model with minimum transaction lots. European Journal of Operational Research 242: 933–41. [Google Scholar] [CrossRef]
- Maillet, Bertrand, Sessi Tokpavi, and Benoit Vaucher. 2015. Global minimum variance portfolio optimization under some model risk: A robust regression-based approach. European Journal of Operational Research 244: 289–99. [Google Scholar] [CrossRef]
- Mainik, Georg, and Eric Schaanning. 2012. On dependence consistency of CoVaR and some other systemic risk measures. Statistics and Risk Modeling 31: 49–77. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1963. The variation of certain speculative prices. Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. Journal of Finance 7: 77–91. [Google Scholar]
- Markowitz, H. M. 1959. Portfolio Selection: Efficient Diversification of Investments. New York: Wiley. [Google Scholar]
- Markowitz, Harry. 1993. Computation of mean-semi variance efficient sets by the critical line algorithm. Annals of Operations Research 45: 307–17. [Google Scholar] [CrossRef]
- Mashal, Roy, and Assaf Zeevi. 2002. Beyond Correlation: Extreme Co-Movements between financial Assets. Technical Report. New York: Columbia University. [Google Scholar]
- Maugis, Pierre André, and Dominique Guegan. 2010. An econometric study of vine copulas. International Journal of Finance and Economics 2: 1–13. [Google Scholar] [CrossRef]
- McAleer, Michael. 2005. Automated inference and learning in modeling financial volatility. Econometric Theory 21: 232–61. [Google Scholar] [CrossRef]
- McAleer, Michael. 2019a. What They Did Not Tell You About Algebraic (Non-)Existence, Mathematical (IR-)Regularity and (Non-)Asymptotic Properties of the Dynamic Conditional Correlation (DCC) Model*. Journal of Risk and Financial Management. under processing. [Google Scholar]
- McAleer, Michael. 2019b. What They Did Not Tell You About Algebraic (Non-)Existence, Mathematical (IR-)Regularity and (Non-)Asymptotic Properties of the Full BEKK Dynamic Conditional Covariance Model*. Journal of Risk and Financial Management. under processing. [Google Scholar]
- Mcaleer, Michael, Felix Chan, Suhejla Hoti, and Offer Lieberman. 2008. Generalized autoregressive conditional correlation. Econometric Theory 24: 1554–83. [Google Scholar] [CrossRef]
- McCulloch, J. Huston. 1985. Miscellanea on Heteros* edasticity. Econometrica (pre-1986) 53: 483. [Google Scholar]
- McKay, Ralph, and T. Erle Keefer. 1996. VaR Is a Dangerous Technique. Corporate Finance Searching for Systems Integration Supplement, 30. [Google Scholar]
- Mendes, Beatriz Vaz de Melo, and Daniel S. Marques. 2012. Choosing an optimal investment strategy: The role of robust pair-Copulas based portfolios. Emerging Markets Review 13: 449–64. [Google Scholar] [CrossRef]
- Merton, Robert. 1969. Life time portfolio selection under uncertainty: The continuous-time case. The review of Economics and Statistics 51: 247–57. [Google Scholar] [CrossRef]
- Merton, Robert. 1971. Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory 3: 373–413. [Google Scholar] [CrossRef]
- Merton, Robert. 1972. An analytic derivation of the efficient portfolio frontier. Journal of Financial and Quantitative Analysis 7: 1851–72. [Google Scholar] [CrossRef]
- Metaxiotis, Kostas S., and Konstantinos Liagkouras. 2012. Multiobjective Evolutionary Algorithms for Portfolio Management: A comprehensive Literature Review. Expert Systems with Applications 39: 11685–98. [Google Scholar] [CrossRef]
- Miller, Douglas J., and Weihan Liu. 2006. Improved estimation of portfolio value-at-risk under copula models with mixed marginals. Journal of Futures Markets 26: 997–1018. [Google Scholar] [CrossRef]
- Morgan, J. P. 1996. Risk Metrics-Technical Document, 4th ed. New York: Morgan Guaranty Trust Company, Available online: https://www.RiskMetrics.com (accessed on 8 March 2019).
- Mori, Harunori. 2004. Finite sample properties of estimators for the optimal portfolio weight. Journal of the Japan Statistical Society 34: 27–46. [Google Scholar] [CrossRef]
- Morton, Andrew J., and Stanley R. Pliska. 1995. Optimal portfolio management with fixed transaction costs. Mathematical Finance 5: 337–56. [Google Scholar] [CrossRef]
- Naimy, Viviene Y. 2016. Testing VaR Accuracy for CDS Portfolios Using Historical Simulation and Delta-Normal Models. Journal of Mathematics and Statistics 12: 99–106. [Google Scholar] [CrossRef]
- Najafi, Amir Abbas, and Siamak Mushakhian. 2015. Multi-stage stochastic mean-semivariance-CVaR portfolio optimization under transaction costs. Applied Mathematics and Computation 256: 445–58. [Google Scholar] [CrossRef]
- Nantell, Timothy J., and Barbara Price. 1979. An Analytical Comparison of Variance and Semivariance Capital Market Theories. Journal of Financial and Quantitative Analysis 14: 221–42. [Google Scholar] [CrossRef]
- Nelsen, Roger. 1999. An Introduction to Copulas. Lecture Notes in Statistics. New York: Springer. [Google Scholar]
- Nguyen, Tilo, and Gennady Samorodnitsky. 2013. Muitivariate tail estimation with application to analysis of CoVaR. Astin Bulletin 43: 245–70. [Google Scholar] [CrossRef]
- Okhrin, Yarema, and Wolfgang Schmid. 2006. Distributional properties of portfolio weights. Journal of Econometrics 134: 235–56. [Google Scholar] [CrossRef]
- Okhrin, Yarema, and Wolfgang Schmid. 2007. Comparison of different estimation techniques for portfolio selection. Asta Advances in Statistical Analysis 91: 109–27. [Google Scholar] [CrossRef]
- Oksendal, Bernt, and Agnès Sulem. 2002. Optimal consumption and portfolio with both fixed and proportional transaction costs. SIAM Journal on Control and Optimization 40: 1765–90. [Google Scholar] [CrossRef]
- Pastpipatkul, Pathairat, Woraphon Yamaka, and Songsak Sriboonchitta. 2018. Portfolio Selection with Stock, Gold and Bond in Thailand Under Vine Copulas Functions. Econometrics for Financial Applications 760: 698–711. [Google Scholar]
- Patton, Andrew J. 2004. On the Out-of-Sample Importance of Skewness and Asymmetric Dependence for Asset Allocation. Journal of Financial Econometrics 2: 130–68. [Google Scholar] [CrossRef]
- Patton, Andrew J. 2006. Modelling asymmetric exchange rate dependence. International Economic Review 47: 527–56. [Google Scholar] [CrossRef]
- Peng, Hui, Genshiro Kitagawa, Min Gan, and Xiaohong Chen. 2011. A new optimal portfolio selection strategy based on a quadratic form mean-variance model with transaction costs. Optimal Control Applications and Methods 32: 127–38. [Google Scholar] [CrossRef]
- Pflug, Georg Ch. 2000. Some remarks on the value-at-risk and the conditional value-at-risk. In Probabilistic Constrained Optimization: Methodology and Applications. Edited by Stanislav Uryasev. Dordrecht: Kluwer. [Google Scholar]
- Pogue, Gerald A. 1970. An extension of the Markowitz portfolio selection model to include variable transactions’ costs, short sales, leverage policies and taxes. The Journal of Finance 25: 1005–27. [Google Scholar] [CrossRef]
- Polasek, Wolfgang, Shuangzhe Liu, and Heinz Neudecker. 2007. Heteroskedastic linear regression models. In Encyclopedia of Statistical Sciences. Edited by Samuel Kotz, C. B. Read, N. Balakrishnan and Brani Vidakovic. New York: Wiley, Available online: https://onlinelibrary.wiley.com/doi/full/10.1002/0471667196.ess1059.pub3 (accessed on 8 March 2019).
- Porter, R. Burr. 1974. Semi-variance and Stochastic Dominance: A Comparison. American Economic Review 64: 200–4. [Google Scholar]
- Rockafellar, R. Tyrrell, and Stanislav P. Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking and Finance 26: 1443–71. [Google Scholar] [CrossRef]
- Rom, Brian M., and Kathleen W. Ferguson. 1994. Post-modern portfolio theory comes of age. Journal of Investing 3: 11–17. [Google Scholar] [CrossRef]
- Rothman, Adam J., Elizaveta Levina, and Ji Zhu. 2009. Generalized thresholding of large covariance matrices. Journal of the American Statistical Association 104: 177–86. [Google Scholar] [CrossRef]
- Roy, Arthur D. 1952. Safety First and the Holding of Assets. Econometrica 20: 431–49. [Google Scholar] [CrossRef]
- Roy, Rahul, and Santhakumar Shijin. 2018. A six-factor asset pricing model. Borsa Istanbul Review 18: 205–17. [Google Scholar] [CrossRef]
- Sak, Halis, Wolfgang Hörmann, and Josef Leydold. 2010. Efficient risk simulations for linear asset portfolios in the t-Copula model. European Journal of Operational Research 202: 802–9. [Google Scholar] [CrossRef]
- Salah, Hanene, Ali Gannoun, Christian De Peretti, and Mathieu Ribatet. 2016. Conditional Mean-Variance and Mean-Semivariance Models in Portfolio Optimization. Working Papers, HAL Id: Hal-01404752. Available online: https://hal.inria.fr/hal-01404752 (accessed on 8 March 2019).
- Samuelson, Paul A. 1969. Lifetime portfolio selection by dynamic stochastic programming. The Review of Economics and Statistics 51: 239–46. [Google Scholar] [CrossRef]
- Santos, André A. P., and Guilherme V. Moura. 2014. Dynamic factor multivariate GARCH model. Computational Statistics and Data Analysis 76: 606–17. [Google Scholar] [CrossRef]
- Sayilgan, Güven, and Arma Mut. 2010. Uses of Variance and Lower Partial Moment Measures for Portfolio Optimization. Journal of Banking and Financial Markets 4: 7–73. [Google Scholar]
- Serfling, Robert. 2002. Quantile functions for multivariate analysis: Approaches and applications. Statistica Neerlandica 56: 214–32. [Google Scholar] [CrossRef]
- Sharpe, William F. 1963. A simplified model for portfolio analysis. Management Science 9: 277–93. [Google Scholar] [CrossRef]
- Simaan, Yusif. 2014. The opportunity cost of mean-variance choice under estimation risk. European Journal of Operational Research 234: 382–91. [Google Scholar] [CrossRef]
- Sira, Enrique. 2006. Semivariance as real project portfolio optimisation criteria an oil and gas industry application. International Journal of Global Energy Issues 26: 43–61. [Google Scholar] [CrossRef]
- Sklar, A. 1959. Fonctions derépartitionàn dimensions et leurs marges. Publication Institute Statistics University Paris 8: 229–31. [Google Scholar]
- So, Mike Ka Pui, and Cherry Y. T. Yeung. 2014. Vine-copula GARCH model with dynamic conditional dependence. Computational Statistics and Data Analysis 76: 655–71. [Google Scholar] [CrossRef]
- Soleimani, Hamed, Hamid Reza Golmakani, and Mohammad Hossein Salimi. 2009. Markowitz-based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm. Expert Systems with Applications 36: 5058–63. [Google Scholar] [CrossRef]
- Sornette, Didier, Joergen Vitting Andersen, and Prospero Simonetti. 2000. Portfolio theory for “fat tails”. International Journal of Theoretical and Applied Finance 3: 523–35. [Google Scholar] [CrossRef]
- Stambaugh, Robert F., and Yu Yuan. 2017. Mispricing Factors. The Review of Financial Studies 30: 1270–315. [Google Scholar] [CrossRef]
- Stevens, Guy V. G. 1998. On the inverse of the covariance matrix in portfolio analysis. Journal of Finance 53: 1821–27. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2002. Forecasting using principal components from a large number of predictors. Journal of the American Statistical Association 97: 1167–79. [Google Scholar] [CrossRef]
- Stone, Bernell K. 1973. A General Class of Three-Parameter Risk Measures. Journal of Finance 28: 675–85. [Google Scholar] [CrossRef]
- Sun, Ruili, Tiefeng Ma, and Shuangzhe Liu. 2018. A Stein-type shrinkage estimator of the covariance matrix for portfolio selections. Metrika, 931–52. [Google Scholar] [CrossRef]
- Sun, Ruili, Tiefeng Ma, and Shuangzhe Liu. 2019. Portfolio selection based on semivariance and distance correlation under minimum variance framework. Statistica Neerlandica. [Google Scholar] [CrossRef]
- Szegö, Georgio. 2002. Measures of risk. Journal of Banking and Finance 26: 1253–72. [Google Scholar] [CrossRef]
- Topaloglou, Nikolas, Hercules Vladimirou, and Stavros A. Zenios. 2008. A dynamic stochastic programming model for international portfolio management. European Journal of Operational Research 185: 1501–24. [Google Scholar] [CrossRef]
- Touloumis, Anestis. 2015. Nonparametric Stein-type shrinkage covariance matrix estimators in high-dimensional setting. Computational Statistics and Data Analysis 83: 251–61. [Google Scholar] [CrossRef]
- Trivedi, Pravin K., and David M. Zimmer. 2006. Using Trivariate Copulas to Model Sample Selection and Treatment Effects: Application to Family Health Care Demand. Journal of Business and Economic Statistics 24: 63–76. [Google Scholar]
- Tsay, Ruey S. 2010. Analysis of Financial Time Series, 3rd ed. Hoboken: John Wiley & Sons. [Google Scholar]
- Tse, Yiu Kuen. 2000. A test for constant correlations in a multivariate GARCH model. Journal of Econometrics 98: 107–27. [Google Scholar] [CrossRef]
- Tse, Yiu Kuen, and Albert K. C. Tsui. 2002. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. Journal of Business and Economics Statistics 20: 351–62. [Google Scholar] [CrossRef]
- Tse, Kwok Sang Maurice, Jamshed Y. Uppal, and Mark A. White. 1993. Downside risk and investment choice. The Financial Review 28: 585. [Google Scholar]
- Tsui, Albert K., and Qiao Yu. 1999. Constant conditional correlation in a bivariate GARCH model: Evidence from the stock markets of China. Mathematics and Computers in Simulation 48: 503–9. [Google Scholar] [CrossRef]
- Tu, Anthony H., and Cathy Yi-Hsuan Chen. 2018. A factor-based approach of bond portfolio value-at-risk: The informational roles of macroeconomic and financial stress factors. Journal of Empirical Finance 45: 243–68. [Google Scholar] [CrossRef]
- Upton, David E., and Donald S. Shannon. 1979. The stable paretian distribution, subordinated stochastic processes, and asymptotic lognormality: An empirical investigation. Journal of Finance 34: 1031–39. [Google Scholar] [CrossRef]
- Uryasev, Stanislav. 2000. Optimization of Conditional Value-at-Risk. The Journal of Risk 2: 21–41. [Google Scholar]
- Van den Goorbergh, Rob W. J., Christian Genest, and Bas J. M. Werker. 2005. Bivariate option pricing using dynamic copula. Mathematics and Economics 37: 101–14. [Google Scholar] [CrossRef]
- Weide, Roy van der. 2002. GO-GARCH: A multivariate generalized orthogonal GARCH model. Journal of Applied Econometrics 17: 549–64. [Google Scholar] [CrossRef]
- Vrontos, Ioannis D., Petros Dellaportas, and Dimitris N. Politis. 2003. A full-factor multivariate GARCH model. The Econometrics Journal 6: 312–34. [Google Scholar] [CrossRef]
- Wang, Ching-Ping, and Hung-Hsi Huang. 2016. Optimal insurance contract under VaR and CVaR constraints. The North American Journal of Economics and Finance 37: 110–27. [Google Scholar] [CrossRef]
- Wang, Zhen, and Sanyang Liu. 2013. Multi-period mean-variance portfolio selection with fixed and proportional transaction costs. Journal of Industrial and Management Optimization 9: 643–57. [Google Scholar]
- Wang, Ching-Ping, David Shyu, and Hung-Hsi Huang. 2005. Optimal insurance design under a value-at-risk framework. The Geneva Risk and Insurance Review 30: 161–79. [Google Scholar] [CrossRef]
- Wang, Xiaoyu, Dejun Xie, Jingjing Jiang, Xiaoxia Wu, and Jia He. 2017. Value-at-Risk estimation with stochastic interest rate models for option-bond portfolios. Finance Research Letters 21: 10–20. [Google Scholar] [CrossRef]
- Watson, Mark, and Robert F. Engle. 1983. Alternative algorithms for the estimation of dynamic factor, mimic and varying coefficient regression models. Journal of Econometrics 23: 385–400. [Google Scholar] [CrossRef]
- Wei, Yu, Yudong Wang, and Dengshi Huang. 2010. Forecasting crude oil market volatility: Further evidence using GARCH-class models. Energy Economics 32: 1477–84. [Google Scholar] [CrossRef]
- Wong, C. S., W. S. Chan, and P. L. Kam. 2009. A Student t-mixture autoregressive model with applications to fat-tailed financial data. Biometrika 96: 751–60. [Google Scholar] [CrossRef]
- Wu, Huiling, and Hua Chen. 2015. Nash equilibrium strategy for a multi-period mean-variance portfolio selection problem with regime switching. Economic Modelling 46: 79–90. [Google Scholar] [CrossRef]
- Wu, Huiling, and Zhongfei Li. 2011. Multi-period mean-variance portfolio selection with Markov regime switching and uncertain time-horizon. Journal of Systems Science and Complexity 24: 140–55. [Google Scholar] [CrossRef]
- Xie, Shuxiang, Zhongfei Li, and Shouyang Wang. 2008. Continuous-time portfolio selection with liability: Mean-variance model and stochastic LQ approach. Insurance: Mathematics and Economics 42: 943–53. [Google Scholar] [CrossRef]
- Xu, Yingying, and Zhuwu Wu. 2014. Continuous-time mean-variance portfolio selection with inflation in an incomplete market. Journal of Financial Risk Management 3: 19–28. [Google Scholar] [CrossRef]
- Xue, Hong-Gang, Cheng-Xian Xu, and Zong-Xian Feng. 2006. Mean-variance portfolio optimal problem under concave transaction cost. Applied Mathematics and Computation 174: 1–12. [Google Scholar] [CrossRef]
- Yang, Liusha, Romain Couillet, and Matthew R. McKay. 2014. Minimum variance portfolio optimization with robust shrinkage covariance estimation. Paper presented at 2014 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, November 2–5; pp. 1326–30. [Google Scholar]
- Yang, Liusha, Romain Couillet, and Matthew R. McKay. 2015. A Robust Statistics Approach to Minimum Variance Portfolio Optimization. IEEE Transactions on Signal Processing 63: 6684–97. [Google Scholar] [CrossRef]
- Yi, Lan, Zhongfei Li, and Duan Li. 2008. Multi-period portfolio selection for asset-liability management with uncertain investment horizon. Journal of Industrial and Management Optimization 4: 535–52. [Google Scholar]
- Yoshimoto, Atsushi. 1996. The mean-variance approach to portfolio optimization subject to transaction costs. Journal of the Operations Research Society of Japan 39: 99–117. [Google Scholar] [CrossRef]
- Zhang, Peng. 2015. Multi-period Possibilistic Mean Semivariance Portfolio Selection with Cardinality Constraints and its Algorithm. Journal of Mathematical Modelling and Algorithms in Operations Research 14: 239–53. [Google Scholar] [CrossRef]
- Zhang, Qingye, and Yan Gao. 2017. Portfolio selection based on a benchmark process with dynamic value-at-risk constraints. Journal of Computational and Applied Mathematics 313: 440–47. [Google Scholar] [CrossRef]
- Zhang, Fan, and Zhichao Zhang. 2018. Strategic asset allocation by mixing shrinkage, vine copula and market equilibrium. Journal of Forecasting 37: 340–51. [Google Scholar] [CrossRef]
- Zhang, Wei-Guo, Qin Mei, Qian Lu, and Wei-Lin Xiao. 2011. Evaluating methods of investment project and optimizing models of portfolio selection in fuzzy uncertainty. Computers and Industrial Engineering 61: 721–28. [Google Scholar] [CrossRef]
- Zhang, Wei-Guo, Yong-Jun Liu, and Wei-Jun Xu. 2012. A possibilistic mean-semivariance-entropy model for multi-period portfolio selection with transaction costs. European Journal of Operational Research 222: 341–49. [Google Scholar] [CrossRef]
- Zhao, Pan, and Qingxian Xiao. 2016. Portfolio selection problem with Value-at-Risk constraints under non-extensive statistical mechanics. Journal of Computational and Applied Mathematics 298: 64–71. [Google Scholar] [CrossRef]
- Zhou, Guofu. 2002. Financial Econometrics: Empirical Analysis of Asset Pricing. Beijing: Peking University Press. [Google Scholar]



| Author | Year | Paper/Book/Thesis Title (Please See References for Details) |
|---|---|---|
| Sklar | 1959 | Fonctions derépartitionàn dimensions et leurs marges |
| Joe | 1997 | Multivariate Models and Dependence Concepts |
| Embrechts | 1999 | An Introduction to Copulas |
| Mashal and Zeevi | 2002 | Beyond correlation: Extreme co-movements between financial assets |
| Van den Goorbergh et al. | 2005 | Bivariate option pricing using dynamic copula models |
| Kole et al. | 2007 | Selecting Copulas for risk management |
| Hafner and Reznikova | 2010 | Efficient estimation of a semiparametric dynamic copula model |
| Author | Year | Paper/Book/Thesis Title (Please See References for Details) |
|---|---|---|
| Markowitz | 1952 | Portfolio Selection |
| Samuelson | 1969 | Lifetime portfolio selection by dynamic stochastic programming |
| Merton | 1969 | Life time portfolio selection under uncertainty: The continuous-time case |
| Pogue | 1970 | An extension of the Markowitz portfolio selection model to include variable transactions’ costs, short sales, leverage policies and taxes |
| Merton | 1972 | An analytic derivation of the efficient portfolio frontier |
| Fernández and Gómez | 2007 | Portfolio selection using neural networks |
| Author | Year | Paper/Book/Thesis Title (Please See References for Details) |
|---|---|---|
| Engle | 1982 | Autoregressive conditional heteroscedasticity and estimates of UK inflation |
| Engle et al. | 1984 | Combining competing forecasts of inflation using a bivariate ARCH model |
| Bollerslev | 1986 | Generalized autoregressive conditional heteroscedasticity |
| Bollerslev et al. | 1988 | A capital asset pricing model with time-varying covariances |
| Bollerslev | 1990 | Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model |
| Engle and Kroner | 1995 | Multivariate simultaneous generalized ARCH |
| Tse and Tsui | 2002 | A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations |
| Engle | 2002 | Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models |
| McAleer et al. | 2008 | Generalized autoregressive conditional correlation |
| Author | Year | Paper/Book/Thesis Title (Please See References for Details) |
|---|---|---|
| Baumol | 1952 | The transactions demand for cash: An inventory theoretic approach |
| Goldfarb and Iyengar | 2003 | Robust portfolio selection problems |
| McKay and Keefer | 1996 | VaR Is a Dangerous Technique |
| Artzner et al. | 1997 | Thinking coherently |
| Pflug | 2000 | Some remarks on the value-at-risk and the conditional value-at-risk |
| Uryasev | 2000 | Optimization of Conditional Value-at-Risk |
| Chen and Yang | 2017 | Multiperiod portfolio investment using stochastic programming with conditional value at risk |
| Zhang and Gao | 2017 | Portfolio selection based on a benchmark process with dynamic value-at-risk constraints |
| Author | Year | Paper/Book/Thesis Title (Please See References for Details) |
|---|---|---|
| Roy | 1952 | Safety First and the Holding of Assets |
| Markowitz | 1959 | Portfolio selection: Efficient diversification of investments |
| Bawa and Lindenberg | 1977 | Capital market equilibrium in a mean-lower partial moment framework |
| Bawa | 1978 | Safety-first, stochastic dominance, and optimal portfolio choice |
| Chen et al. | 1991 | A Method for Approximating Semivariance in Project Portfolio Analysis |
| Hamza and Janssen | 1998 | The mean-semivariances approach to realistic portfolio optimization subject to transaction costs |
| Ballestero | 2005 | Mean-semivariance efficient frontier: A downside risk model for portfolio selection |
| Huang | 2008 | Mean-semi variance models for fuzzy portfolio selection |
| Sayilgan and Mut | 2010 | Uses of Variance and Lower Partial Moment Measures for Portfolio Optimization |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Ma, T.; Liu, S.; Sathye, M. Improved Covariance Matrix Estimation for Portfolio Risk Measurement: A Review. J. Risk Financial Manag. 2019, 12, 48. https://doi.org/10.3390/jrfm12010048
Sun R, Ma T, Liu S, Sathye M. Improved Covariance Matrix Estimation for Portfolio Risk Measurement: A Review. Journal of Risk and Financial Management. 2019; 12(1):48. https://doi.org/10.3390/jrfm12010048
Chicago/Turabian StyleSun, Ruili, Tiefeng Ma, Shuangzhe Liu, and Milind Sathye. 2019. "Improved Covariance Matrix Estimation for Portfolio Risk Measurement: A Review" Journal of Risk and Financial Management 12, no. 1: 48. https://doi.org/10.3390/jrfm12010048
APA StyleSun, R., Ma, T., Liu, S., & Sathye, M. (2019). Improved Covariance Matrix Estimation for Portfolio Risk Measurement: A Review. Journal of Risk and Financial Management, 12(1), 48. https://doi.org/10.3390/jrfm12010048